|
Thyra
Version of the Day
|
|
Thyra
Version of the Day
|
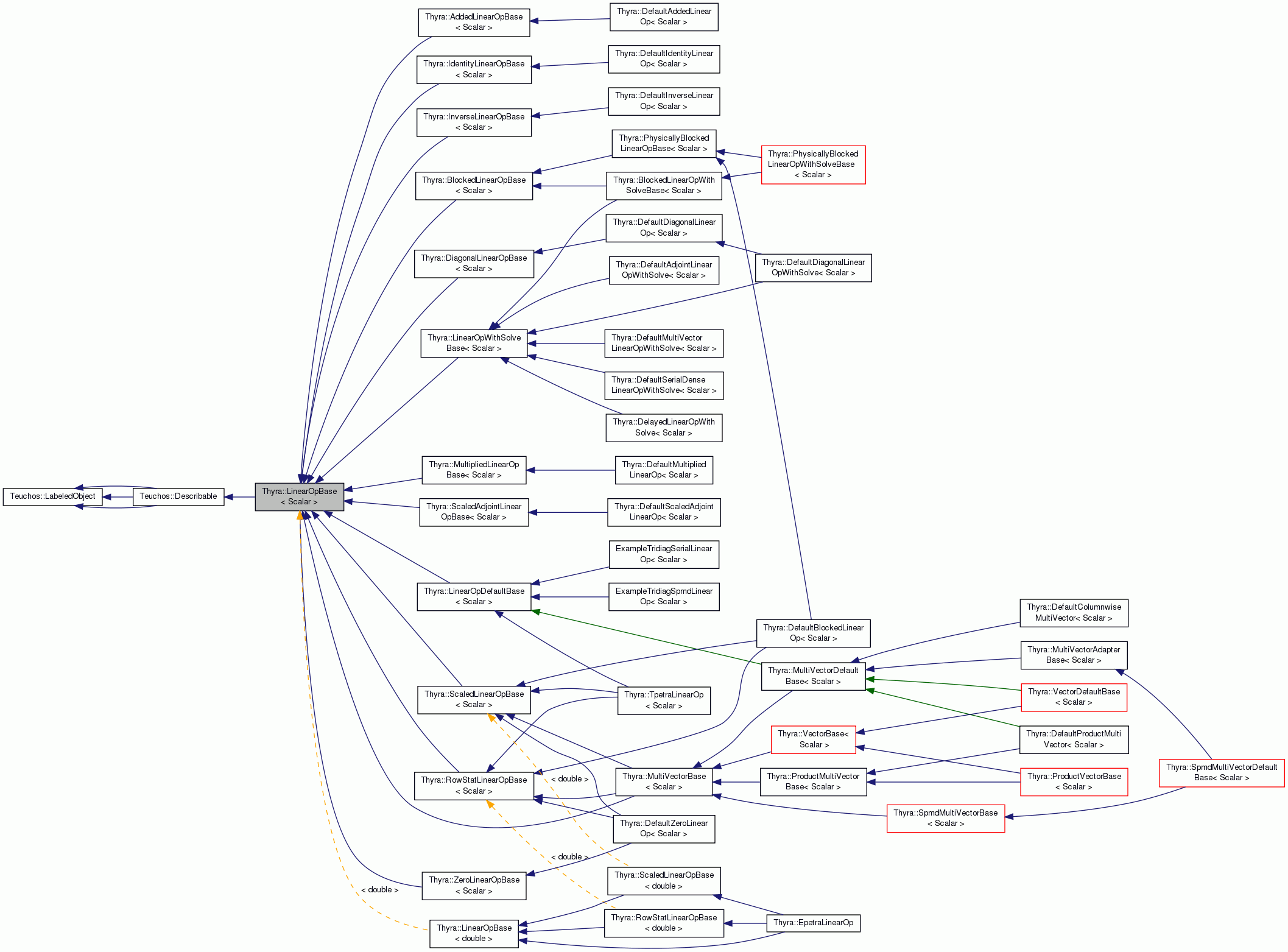
Base class for all linear operators. More...
#include <Thyra_LinearOpBase_decl.hpp>
Related Functions | |
(Note that these are not member functions.) | |
| template<class Scalar > | |
| bool | isFullyUninitialized (const LinearOpBase< Scalar > &M) |
| Determines if a linear operator is in the "Fully Uninitialized" state or not. More... | |
| template<class Scalar > | |
| bool | isPartiallyInitialized (const LinearOpBase< Scalar > &M) |
| Determines if a linear operator is in the "Partially Initialized" state or not. More... | |
| template<class Scalar > | |
| bool | isFullyInitialized (const LinearOpBase< Scalar > &M) |
| Determines if a linear operator is in the "Fully Initialized" state or not. More... | |
| template<class Scalar > | |
| bool | opSupported (const LinearOpBase< Scalar > &M, EOpTransp M_trans) |
| Determines if an operation is supported for a single scalar type. More... | |
| template<class Scalar > | |
| void | apply (const LinearOpBase< Scalar > &M, const EOpTransp M_trans, const MultiVectorBase< Scalar > &X, const Ptr< MultiVectorBase< Scalar > > &Y, const Scalar alpha=static_cast< Scalar >(1.0), const Scalar beta=static_cast< Scalar >(0.0)) |
Non-member function call for M.apply(...). More... | |
| void | apply (const LinearOpBase< double > &M, const EOpTransp M_trans, const MultiVectorBase< double > &X, const Ptr< MultiVectorBase< double > > &Y, const double alpha=1.0, const double beta=0.0) |
Calls apply<double>(...). More... | |
Public interface functions | |
| virtual RCP< const VectorSpaceBase< Scalar > > | range () const =0 |
Return a smart pointer for the range space for this operator. More... | |
| virtual RCP< const VectorSpaceBase< Scalar > > | domain () const =0 |
Return a smart pointer for the domain space for this operator. More... | |
| bool | opSupported (EOpTransp M_trans) const |
Return if the M_trans operation of apply() is supported or not. More... | |
| void | apply (const EOpTransp M_trans, const MultiVectorBase< Scalar > &X, const Ptr< MultiVectorBase< Scalar > > &Y, const Scalar alpha, const Scalar beta) const |
Apply the linear operator to a multi-vector : Y = alpha*op(M)*X + beta*Y. More... | |
| virtual RCP< const LinearOpBase< Scalar > > | clone () const |
| Clone the linear operator object (if supported). More... | |
Protected virtual functions to be overridden by subclasses. | |
| virtual bool | opSupportedImpl (EOpTransp M_trans) const =0 |
| Override in subclass. More... | |
| virtual void | applyImpl (const EOpTransp M_trans, const MultiVectorBase< Scalar > &X, const Ptr< MultiVectorBase< Scalar > > &Y, const Scalar alpha, const Scalar beta) const =0 |
| Override in subclass. More... | |
Base class for all linear operators.
A linear operator can optionally perform following operations
Y = alpha*M*X + beta*Y
Y = alpha*conjugate(M)*X + beta*Y
Y = alpha*transpose(M)*X + beta*Y
Y = alpha*adjoint(M)*X + beta*Y
through the apply() function where Y and X are MultiVectorBase objects. The reason for the exact form of the above operations is that there are direct BLAS and equivalent versions of these operations and performing a sum-into multiplication is more efficient in general.
A linear operator has vector spaces associated with it for the vectors x and y that lie in the domain and the range spaces of the non-transposed linear operator y = M*x. These spaces are returned by domain() and range().
Note that the vector spaces returned from domain() and range() may have specialized implementations of the scalar product 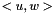 (i.e.
(i.e. 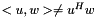 in general). As a result, the operator and adjoint operator must obey the defined scalar products. Specifically, for any two vectors
in general). As a result, the operator and adjoint operator must obey the defined scalar products. Specifically, for any two vectors 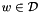 (in the domain space of
(in the domain space of A) and 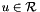 (in the range space of
(in the range space of A), the adjoint operation must obey the adjoint property
![\[ <u,A v>_{\mathcal{R}} =\!= <A^H u, v>_{\mathcal{D}} \]](form_22.png)
where 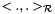 is the scalar product defined by
is the scalar product defined by this->range()->scalarProd() and 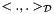 is the scalar product defined by
is the scalar product defined by this->domain()->scalarProd(). This property of the adjoint can be checked numerically, if adjoints are supported, using the testing utility class LinearOpTester.
It is strictly forbidden to alias the input/output object Y with the input object X in apply(). Allowing aliasing would greatly complicate the development of concrete subclasses.
This interface does not require that a linear operator implementation support all of the different types of operator applications defined in the introduction above. If a LinearOpBase object can not support a particular type of operator application, then this is determined by the functions opSupported().
The concrete class LinearOpTester provides a full featured set of tests for any LinearOpBase object. This testing class can check if the operator is truly "linear", and/or if the adjoint relationship holds, and/or if an operator is symmetric. All of the tests are controlled by the client, can be turned on and off, and pass/failure is determined by tolerances that the client can specify. In addition, this testing class can also check if two linear operators are approximately equal.
A LinearOpBase object has three different states of initialization. These three initailziation states, a description of their definition, and non-member helper functions that return these states are given below:
Fully Uninitialized: State: (is_null(this->range()) && is_null(this->domain())), Nonmember function: isFullyUninitialized()
Partially Initialized: State: (!is_null(this->range()) && !is_null(this->domain())) && (!this->opSupported(M_trans)) for all values of M_trans, Nonmember function: isPartiallyInitialized()
Fully Initialized: State: (!is_null(this->range()) && !is_null(this->domain())) && (this->opSupported(M_trans) for at least one valid value for M_trans, Nonmember function: isFullyInitialized()
These three different states of initialization allow for the simplification of the implementation of many different types of use cases.
There are only foure functions that a concrete subclass is required to override: domain(), range() opSupportedImpl(), and applyImpl(). Note that the functions domain() and range() should simply return VectorSpaceBase objects for subclasses that are already defined for the vectors that the linear operator interacts with through the function apply(). The function opSupportedImpl() just returns what operations are supported and is therefore trivial to implement. Therefore, given that appropriate VectorSpaceBase and MultiVectorBase (and/or VectorBase) subclasses exist, the only real work involved in implementing a LinearOpBase subclass is in defining a single function applyImpl().
If possible, the subclass should also override the clone() function which allows clients to create copies of a LinearOpBase object. This functionality is useful in some circumstances. However, this functionality is not required and the default clone() implementation returns a null smart pointer object.
Definition at line 159 of file Thyra_LinearOpBase_decl.hpp.
|
pure virtual |
Return a smart pointer for the range space for this operator.
Note that a return value of is_null(returnVal) is a flag that *this is not fully initialized.
If nonnull(returnVal), it is required that the object referenced by *returnVal must have lifetime that extends past the lifetime of the returned smart pointer object. However, the object referenced by *returnVal may change if *this modified so this reference should not be maintained for too long.
New Behavior! It is required that the VectorSpaceBase object embedded in return must be valid past the lifetime of *this linear operator object.
Implemented in Thyra::EpetraLinearOp, Thyra::DefaultScaledAdjointLinearOp< Scalar >, Thyra::DefaultInverseLinearOp< Scalar >, Thyra::DefaultBlockedTriangularLinearOpWithSolve< Scalar >, Thyra::DefaultDiagonalLinearOp< Scalar >, Thyra::DefaultMultipliedLinearOp< Scalar >, ExampleTridiagSpmdLinearOp< Scalar >, Thyra::DefaultAddedLinearOp< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::DefaultBlockedLinearOp< Scalar >, Thyra::DefaultProductMultiVector< Scalar >, ExampleTridiagSerialLinearOp< Scalar >, Thyra::DefaultZeroLinearOp< Scalar >, Thyra::DefaultIdentityLinearOp< Scalar >, Thyra::VectorDefaultBase< Scalar >, Thyra::TpetraLinearOp< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultSerialDenseLinearOpWithSolve< Scalar >, Thyra::DelayedLinearOpWithSolve< Scalar >, Thyra::DefaultMultiVectorLinearOpWithSolve< Scalar >, Thyra::MultiVectorAdapterBase< Scalar >, and Thyra::DefaultAdjointLinearOpWithSolve< Scalar >.
|
pure virtual |
Return a smart pointer for the domain space for this operator.
Note that a return value of is_null(returnVal) is a flag that *this is not fully initialized.
If nonnull(returnVal), it is required that the object referenced by *returnVal must have lifetime that extends past the lifetime of the returned smart pointer object. However, the object referenced by *returnVal may change if *this modified so this reference should not be maintained for too long.
New Behavior! It is required that the VectorSpaceBase object embedded in return must be valid past the lifetime of *this linear operator object.
Implemented in Thyra::EpetraLinearOp, Thyra::DefaultScaledAdjointLinearOp< Scalar >, Thyra::DefaultInverseLinearOp< Scalar >, Thyra::DefaultBlockedTriangularLinearOpWithSolve< Scalar >, Thyra::DefaultDiagonalLinearOp< Scalar >, Thyra::DefaultMultipliedLinearOp< Scalar >, ExampleTridiagSpmdLinearOp< Scalar >, Thyra::DefaultAddedLinearOp< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::DefaultBlockedLinearOp< Scalar >, Thyra::DefaultProductMultiVector< Scalar >, ExampleTridiagSerialLinearOp< Scalar >, Thyra::DefaultZeroLinearOp< Scalar >, Thyra::VectorDefaultBase< Scalar >, Thyra::DefaultIdentityLinearOp< Scalar >, Thyra::TpetraLinearOp< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultSerialDenseLinearOpWithSolve< Scalar >, Thyra::DelayedLinearOpWithSolve< Scalar >, Thyra::DefaultMultiVectorLinearOpWithSolve< Scalar >, Thyra::MultiVectorAdapterBase< Scalar >, Thyra::TpetraVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::DefaultAdjointLinearOpWithSolve< Scalar >.
|
inline |
Return if the M_trans operation of apply() is supported or not.
Preconditions:
isPartiallyInitialized(*this) Note that an operator must support at least one of the values of ETrans (i.e. the transposed or the non-transposed operations must be supported, both can not be unsupported)
Definition at line 210 of file Thyra_LinearOpBase_decl.hpp.
|
inline |
Apply the linear operator to a multi-vector : Y = alpha*op(M)*X + beta*Y.
| M_trans | [in] Determines whether the operator is applied or the adjoint for op(M). |
| X | [in] The right hand side multi-vector. |
| Y | [in/out] The target multi-vector being transformed. When beta==0.0, this multi-vector can have uninitialized elements. |
| alpha | [in] Scalar multiplying M, where M==*this. The default value of alpha is 1.0 |
| beta | [in] The multiplier for the target multi-vector Y. The default value of beta is 0.0. |
Preconditions:
this->opSupported(M_trans)==true (throw Exceptions::OpNotSupported)
X.range()->isCompatible(*op(this)->domain()) == true (throw Exceptions::IncompatibleVectorSpaces)
Y->range()->isCompatible(*op(this)->range()) == true (throw Exceptions::IncompatibleVectorSpaces)
Y->domain()->isCompatible(*X.domain()) == true (throw Exceptions::IncompatibleVectorSpaces)
Y can not alias X. It is up to the client to ensure that Y and X are distinct since in general this can not be verified by the implementation until, perhaps, it is too late. If possible, an exception will be thrown if aliasing is detected.
Postconditions:
Y is transformed as indicated above. Definition at line 260 of file Thyra_LinearOpBase_decl.hpp.
|
virtual |
Clone the linear operator object (if supported).
The primary purpose for this function is to allow a client to capture the current state of a linear operator object and be guaranteed that some other client will not alter its behavior. A smart implementation will use reference counting and lazy evaluation internally and will not actually copy any large amount of data unless it has to.
The default implementation returns is_null(returnVal) which is allowable. A linear operator object is not required to return a non-NULL value but many good matrix-based linear operator implementations will.
Reimplemented in Thyra::MultiVectorBase< Scalar >, Thyra::EpetraLinearOp, Thyra::DefaultScaledAdjointLinearOp< Scalar >, Thyra::DefaultInverseLinearOp< Scalar >, Thyra::DefaultBlockedTriangularLinearOpWithSolve< Scalar >, Thyra::DefaultDiagonalLinearOp< Scalar >, Thyra::DefaultMultipliedLinearOp< Scalar >, Thyra::DefaultAddedLinearOp< Scalar >, Thyra::DefaultBlockedLinearOp< Scalar >, Thyra::DefaultZeroLinearOp< Scalar >, Thyra::DefaultIdentityLinearOp< Scalar >, Thyra::DelayedLinearOpWithSolve< Scalar >, and Thyra::DefaultMultiVectorLinearOpWithSolve< Scalar >.
Definition at line 26 of file Thyra_LinearOpBase_def.hpp.
|
protectedpure virtual |
Override in subclass.
Implemented in Thyra::EpetraLinearOp, Thyra::DefaultScaledAdjointLinearOp< Scalar >, Thyra::VectorDefaultBase< Scalar >, Thyra::DefaultInverseLinearOp< Scalar >, Thyra::DefaultBlockedTriangularLinearOpWithSolve< Scalar >, Thyra::DefaultProductMultiVector< Scalar >, Thyra::DefaultMultipliedLinearOp< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::DefaultDiagonalLinearOp< Scalar >, Thyra::DefaultAddedLinearOp< Scalar >, Thyra::DefaultBlockedLinearOp< Scalar >, ExampleTridiagSpmdLinearOp< Scalar >, Thyra::DefaultZeroLinearOp< Scalar >, Thyra::TpetraLinearOp< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultIdentityLinearOp< Scalar >, ExampleTridiagSerialLinearOp< Scalar >, Thyra::DelayedLinearOpWithSolve< Scalar >, Thyra::DefaultSerialDenseLinearOpWithSolve< Scalar >, Thyra::DefaultMultiVectorLinearOpWithSolve< Scalar >, Thyra::MultiVectorAdapterBase< Scalar >, and Thyra::DefaultAdjointLinearOpWithSolve< Scalar >.
|
protectedpure virtual |
Override in subclass.
Implemented in Thyra::DefaultScaledAdjointLinearOp< Scalar >, Thyra::EpetraLinearOp, Thyra::VectorDefaultBase< Scalar >, Thyra::DefaultInverseLinearOp< Scalar >, Thyra::DefaultBlockedTriangularLinearOpWithSolve< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::DefaultProductMultiVector< Scalar >, Thyra::DefaultMultipliedLinearOp< Scalar >, Thyra::DefaultAddedLinearOp< Scalar >, Thyra::DefaultDiagonalLinearOp< Scalar >, Thyra::TpetraVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultBlockedLinearOp< Scalar >, ExampleTridiagSpmdLinearOp< Scalar >, Thyra::DefaultZeroLinearOp< Scalar >, Thyra::TpetraLinearOp< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultIdentityLinearOp< Scalar >, ExampleTridiagSerialLinearOp< Scalar >, Thyra::DelayedLinearOpWithSolve< Scalar >, Thyra::DefaultSerialDenseLinearOpWithSolve< Scalar >, Thyra::DefaultMultiVectorLinearOpWithSolve< Scalar >, Thyra::MultiVectorAdapterBase< Scalar >, and Thyra::DefaultAdjointLinearOpWithSolve< Scalar >.
|
related |
Determines if a linear operator is in the "Fully Uninitialized" state or not.
|
related |
Determines if a linear operator is in the "Partially Initialized" state or not.
|
related |
Determines if a linear operator is in the "Fully Initialized" state or not.
|
related |
Determines if an operation is supported for a single scalar type.
|
related |
Non-member function call for M.apply(...).
|
related |
Calls apply<double>(...).
Non-tempalted double inlined non-member helper function.
 1.8.5
1.8.5