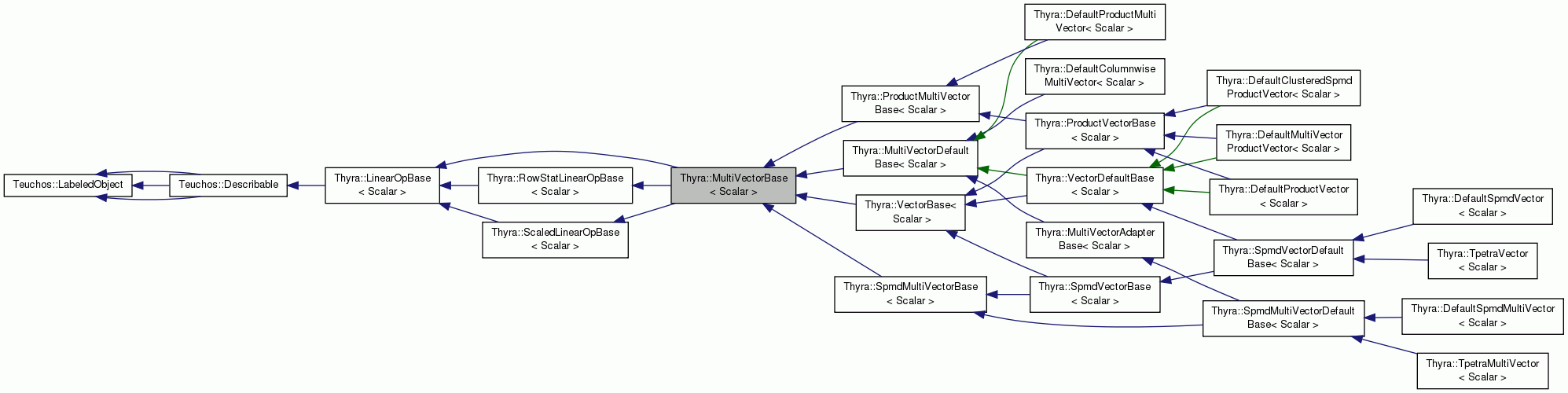
Interface for a collection of column vectors called a multi-vector. More...

#include <Thyra_MultiVectorBase_decl.hpp>

Inheritance diagram for Thyra::MultiVectorBase< Scalar >:

Protected Member Functions
void	absRowSum (const Teuchos::Ptr< Thyra::VectorBase< Scalar > > &output) const

void	absColSum (const Teuchos::Ptr< Thyra::VectorBase< Scalar > > &output) const

Protected Member Functions inherited from Thyra::LinearOpBase< Scalar >
virtual bool	opSupportedImpl (EOpTransp M_trans) const =0
	Override in subclass. More...

virtual void	applyImpl (const EOpTransp M_trans, const MultiVectorBase< Scalar > &X, const Ptr< MultiVectorBase< Scalar > > &Y, const Scalar alpha, const Scalar beta) const =0
	Override in subclass. More...

Protected Member Functions inherited from Thyra::RowStatLinearOpBase< Scalar >
Protected Member Functions inherited from Thyra::ScaledLinearOpBase< Scalar >

Related Functions
(Note that these are not member functions.)
template<class Scalar >
void	applyOp (const RTOpPack::RTOpT< Scalar > &primary_op, const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &multi_vecs, const ArrayView< const Ptr< MultiVectorBase< Scalar > > > &targ_multi_vecs, const ArrayView< const Ptr< RTOpPack::ReductTarget > > &reduct_objs, const Ordinal primary_global_offset=0)
	Apply a reduction/transformation operator column by column and return an array of the reduction objects. More...

template<class Scalar >
void	applyOp (const RTOpPack::RTOpT< Scalar > &primary_op, const RTOpPack::RTOpT< Scalar > &secondary_op, const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &multi_vecs, const ArrayView< const Ptr< MultiVectorBase< Scalar > > > &targ_multi_vecs, const Ptr< RTOpPack::ReductTarget > &reduct_obj, const Ordinal primary_global_offset=0)
	Apply a reduction/transformation operator column by column and reduce the intermediate reduction objects into one reduction object. More...

template<class Scalar >
void	norms (const MultiVectorBase< Scalar > &V, const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &norms)
	Column-wise multi-vector natural norm. More...

template<class Scalar , class NormOp >
void	reductions (const MultiVectorBase< Scalar > &V, const NormOp &op, const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &norms)
	Column-wise multi-vector reductions. More...

template<class Scalar >
void	norms_1 (const MultiVectorBase< Scalar > &V, const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &norms)
	Column-wise multi-vector one norm. More...

template<class Scalar >
void	norms_2 (const MultiVectorBase< Scalar > &V, const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &norms)
	Column-wise multi-vector 2 (Euclidean) norm. More...

template<class Scalar >
void	norms_inf (const MultiVectorBase< Scalar > &V, const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &norms)
	Column-wise multi-vector infinity norm. More...

template<class Scalar >
Array< typename ScalarTraits < Scalar >::magnitudeType >	norms_inf (const MultiVectorBase< Scalar > &V)
	Column-wise multi-vector infinity norm. More...

template<class Scalar >
void	dots (const MultiVectorBase< Scalar > &V1, const MultiVectorBase< Scalar > &V2, const ArrayView< Scalar > &dots)
	Multi-vector dot product. More...

template<class Scalar >
void	sums (const MultiVectorBase< Scalar > &V, const ArrayView< Scalar > &sums)
	Multi-vector column sum. More...

template<class Scalar >
ScalarTraits< Scalar > ::magnitudeType	norm_1 (const MultiVectorBase< Scalar > &V)
	Take the induced matrix one norm of a multi-vector. More...

template<class Scalar >
void	scale (Scalar alpha, const Ptr< MultiVectorBase< Scalar > > &V)
	V = alpha*V. More...

template<class Scalar >
void	scaleUpdate (const VectorBase< Scalar > &a, const MultiVectorBase< Scalar > &U, const Ptr< MultiVectorBase< Scalar > > &V)
	A*U + V -> V (where A is a diagonal matrix with diagonal a). More...

template<class Scalar >
void	assign (const Ptr< MultiVectorBase< Scalar > > &V, Scalar alpha)
	V = alpha. More...

template<class Scalar >
void	assign (const Ptr< MultiVectorBase< Scalar > > &V, const MultiVectorBase< Scalar > &U)
	V = U. More...

template<class Scalar >
void	update (Scalar alpha, const MultiVectorBase< Scalar > &U, const Ptr< MultiVectorBase< Scalar > > &V)
	alpha*U + V -> V. More...

template<class Scalar >
void	update (const ArrayView< const Scalar > &alpha, Scalar beta, const MultiVectorBase< Scalar > &U, const Ptr< MultiVectorBase< Scalar > > &V)
	alpha[j]betaU(j) + V(j) - > V(j), for j = 0 ,,, More...

template<class Scalar >
void	update (const MultiVectorBase< Scalar > &U, const ArrayView< const Scalar > &alpha, Scalar beta, const Ptr< MultiVectorBase< Scalar > > &V)
	U(j) + alpha[j]betaV(j) - > V(j), for j = 0 ,,, U.domain()->dim()-1. More...

template<class Scalar >
void	linear_combination (const ArrayView< const Scalar > &alpha, const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &X, const Scalar &beta, const Ptr< MultiVectorBase< Scalar > > &Y)
	`Y.col(j)(i) = betaY.col(j)(i) + sum( alpha[k]X[k].col(j)(i), k=0...m-1 )`, for `i = 0...Y->range()->dim()-1`, `j = 0...Y->domain()->dim()-1`. More...

template<class Scalar >
void	randomize (Scalar l, Scalar u, const Ptr< MultiVectorBase< Scalar > > &V)
	Generate a random multi-vector with elements uniformly distributed elements. More...

template<class Scalar >
void	Vt_S (const Ptr< MultiVectorBase< Scalar > > &Z, const Scalar &alpha)
	`Z(i,j) *= alpha, i = 0...Z->range()->dim()-1, j = 0...Z->domain()->dim()-1`. More...

template<class Scalar >
void	Vp_S (const Ptr< MultiVectorBase< Scalar > > &Z, const Scalar &alpha)
	`Z(i,j) += alpha, i = 0...Z->range()->dim()-1, j = 0...Z->domain()->dim()-1`. More...

template<class Scalar >
void	Vp_V (const Ptr< MultiVectorBase< Scalar > > &Z, const MultiVectorBase< Scalar > &X)
	`Z(i,j) += X(i,j), i = 0...Z->range()->dim()-1, j = 0...Z->domain()->dim()-1`. More...

template<class Scalar >
void	V_VpV (const Ptr< MultiVectorBase< Scalar > > &Z, const MultiVectorBase< Scalar > &X, const MultiVectorBase< Scalar > &Y)
	`Z(i,j) = X(i,j) + Y(i,j), i = 0...Z->range()->dim()-1, j = 0...Z->domain()->dim()-1`. More...

template<class Scalar >
void	V_VmV (const Ptr< MultiVectorBase< Scalar > > &Z, const MultiVectorBase< Scalar > &X, const MultiVectorBase< Scalar > &Y)
	`Z(i,j) = X(i,j) - Y(i,j), i = 0...Z->range()->dim()-1, j = 0...Z->domain()->dim()-1`. More...

template<class Scalar >
void	V_StVpV (const Ptr< MultiVectorBase< Scalar > > &Z, const Scalar &alpha, const MultiVectorBase< Scalar > &X, const MultiVectorBase< Scalar > &Y)
	`Z(i,j) = alpha*X(i,j) + Y(i), i = 0...z->space()->dim()-1`, , j = 0...Z->domain()->dim()-1. More...

Related Functions inherited from Thyra::LinearOpBase< Scalar >
template<class Scalar >
bool	isFullyUninitialized (const LinearOpBase< Scalar > &M)
	Determines if a linear operator is in the "Fully Uninitialized" state or not. More...

template<class Scalar >
bool	isPartiallyInitialized (const LinearOpBase< Scalar > &M)
	Determines if a linear operator is in the "Partially Initialized" state or not. More...

template<class Scalar >
bool	isFullyInitialized (const LinearOpBase< Scalar > &M)
	Determines if a linear operator is in the "Fully Initialized" state or not. More...

template<class Scalar >
bool	opSupported (const LinearOpBase< Scalar > &M, EOpTransp M_trans)
	Determines if an operation is supported for a single scalar type. More...

template<class Scalar >
void	apply (const LinearOpBase< Scalar > &M, const EOpTransp M_trans, const MultiVectorBase< Scalar > &X, const Ptr< MultiVectorBase< Scalar > > &Y, const Scalar alpha=static_cast< Scalar >(1.0), const Scalar beta=static_cast< Scalar >(0.0))
	Non-member function call for `M.apply(...)`. More...

void	apply (const LinearOpBase< double > &M, const EOpTransp M_trans, const MultiVectorBase< double > &X, const Ptr< MultiVectorBase< double > > &Y, const double alpha=1.0, const double beta=0.0)
	Calls `apply<double>(...)`. More...

Minimal mathematical functions
void	assign (Scalar alpha)
	V = alpha. More...

void	assign (const MultiVectorBase< Scalar > &mv)
	V = mv. More...

void	scale (Scalar alpha)

void	update (Scalar alpha, const MultiVectorBase< Scalar > &mv)

void	linear_combination (const ArrayView< const Scalar > &alpha, const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &mv, const Scalar &beta)
	`Y.col(j)(i) = betaY.col(j)(i) + sum( alpha[k]X[k].col(j)(i),` More...

void	dots (const MultiVectorBase< Scalar > &mv, const ArrayView< Scalar > &prods) const
	Column-wise Euclidean dot product. More...

void	norms_1 (const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &norms) const
	Column-wise 1-norms. More...

void	norms_2 (const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &norms) const
	Column-wise 2-norms. More...

void	norms_inf (const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &norms) const
	Column-wise infinity-norms. More...

Provide access to the columns as VectorBase objects
RCP< const VectorBase< Scalar > >	col (Ordinal j) const
	Calls colImpl(). More...

RCP< VectorBase< Scalar > >	col (Ordinal j)
	Calls nonconstColImpl(). More...

Multi-vector sub-views
RCP< const MultiVectorBase < Scalar > >	subView (const Range1D &colRng) const
	Calls contigSubViewImpl(). More...

RCP< MultiVectorBase< Scalar > >	subView (const Range1D &colRng)
	Calls nonconstContigSubViewImpl(). More...

RCP< const MultiVectorBase < Scalar > >	subView (const ArrayView< const int > &cols) const
	nonContigSubViewImpl(). More...

RCP< MultiVectorBase< Scalar > >	subView (const ArrayView< const int > &cols)
	nonconstNonContigSubViewImpl(). More...

Collective reduction/transformation operator apply functions
void	applyOp (const RTOpPack::RTOpT< Scalar > &primary_op, const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &multi_vecs, const ArrayView< const Ptr< MultiVectorBase< Scalar > > > &targ_multi_vecs, const ArrayView< const Ptr< RTOpPack::ReductTarget > > &reduct_objs, const Ordinal primary_global_offset) const
	Calls mvMultiReductApplyOpImpl(). More...

void	applyOp (const RTOpPack::RTOpT< Scalar > &primary_op, const RTOpPack::RTOpT< Scalar > &secondary_op, const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &multi_vecs, const ArrayView< const Ptr< MultiVectorBase< Scalar > > > &targ_multi_vecs, const Ptr< RTOpPack::ReductTarget > &reduct_obj, const Ordinal primary_global_offset) const
	mvSingleReductApplyOpImpl(). More...

Explicit sub-multi-vector access
void	acquireDetachedView (const Range1D &rowRng, const Range1D &colRng, RTOpPack::ConstSubMultiVectorView< Scalar > *sub_mv) const
	Calls acquireDetachedMultiVectorViewImpl(). More...

void	releaseDetachedView (RTOpPack::ConstSubMultiVectorView< Scalar > *sub_mv) const
	Calls releaseDetachedMultiVectorViewImpl(). More...

void	acquireDetachedView (const Range1D &rowRng, const Range1D &colRng, RTOpPack::SubMultiVectorView< Scalar > *sub_mv)
	Calls acquireNonconstDetachedMultiVectorViewImpl(). More...

void	commitDetachedView (RTOpPack::SubMultiVectorView< Scalar > *sub_mv)
	Calls commitNonconstDetachedMultiVectorViewImpl(). More...

Cloning
virtual RCP< MultiVectorBase < Scalar > >	clone_mv () const =0
	Clone the multi-vector object (if supported). More...

Overridden functions from LinearOpBase
RCP< const LinearOpBase< Scalar > >	clone () const
	This function is simply overridden to return `this->clone_mv()`. More...

Protected virtual functions to be overridden by subclasses
virtual void	assignImpl (Scalar alpha)=0
	Virtual implementation for NVI assign(Scalar). More...

virtual void	assignMultiVecImpl (const MultiVectorBase< Scalar > &mv)=0
	Virtual implementation for NVI assign(MV). More...

virtual void	scaleImpl (Scalar alpha)=0
	Virtual implementation for NVI scale(). More...

virtual void	updateImpl (Scalar alpha, const MultiVectorBase< Scalar > &mv)=0
	Virtual implementation for NVI update(). More...

virtual void	linearCombinationImpl (const ArrayView< const Scalar > &alpha, const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &mv, const Scalar &beta)=0
	Virtual implementation for NVI linear_combination(). More...

virtual void	dotsImpl (const MultiVectorBase< Scalar > &mv, const ArrayView< Scalar > &prods) const =0
	Virtual implementation for NVI dots(). More...

virtual void	norms1Impl (const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &norms) const =0
	Virtual implementation for NVI norms_1(). More...

virtual void	norms2Impl (const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &norms) const =0
	Virtual implementation for NVI norms_2(). More...

virtual void	normsInfImpl (const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &norms) const =0
	Virtual implementation for NVI norms_inf(). More...

virtual RCP< const VectorBase < Scalar > >	colImpl (Ordinal j) const
	Return a non-changeable view of a constituent column vector. More...

virtual RCP< VectorBase< Scalar > >	nonconstColImpl (Ordinal j)=0
	Return a changeable view of a constituent column vector. More...

virtual RCP< const MultiVectorBase< Scalar > >	contigSubViewImpl (const Range1D &colRng) const =0
	Return a non-changeable sub-view of a contiguous set of columns of the this multi-vector. More...

virtual RCP< MultiVectorBase < Scalar > >	nonconstContigSubViewImpl (const Range1D &colRng)=0
	Return a changeable sub-view of a contiguous set of columns of the this multi-vector. More...

virtual RCP< const MultiVectorBase< Scalar > >	nonContigSubViewImpl (const ArrayView< const int > &cols) const =0
	Return a non-changeable sub-view of a non-contiguous set of columns of this multi-vector. More...

virtual RCP< MultiVectorBase < Scalar > >	nonconstNonContigSubViewImpl (const ArrayView< const int > &cols)=0
	Return a changeable sub-view of a non-contiguous set of columns of this multi-vector. More...

virtual void	mvMultiReductApplyOpImpl (const RTOpPack::RTOpT< Scalar > &primary_op, const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &multi_vecs, const ArrayView< const Ptr< MultiVectorBase< Scalar > > > &targ_multi_vecs, const ArrayView< const Ptr< RTOpPack::ReductTarget > > &reduct_objs, const Ordinal primary_global_offset) const =0
	Apply a reduction/transformation operator column by column and return an array of the reduction objects. More...

virtual void	mvSingleReductApplyOpImpl (const RTOpPack::RTOpT< Scalar > &primary_op, const RTOpPack::RTOpT< Scalar > &secondary_op, const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &multi_vecs, const ArrayView< const Ptr< MultiVectorBase< Scalar > > > &targ_multi_vecs, const Ptr< RTOpPack::ReductTarget > &reduct_obj, const Ordinal primary_global_offset) const =0
	Apply a reduction/transformation operator column by column and reduce the intermediate reduction objects into a single reduction object. More...

virtual void	acquireDetachedMultiVectorViewImpl (const Range1D &rowRng, const Range1D &colRng, RTOpPack::ConstSubMultiVectorView< Scalar > *sub_mv) const =0
	Get a non-changeable explicit view of a sub-multi-vector. More...

virtual void	releaseDetachedMultiVectorViewImpl (RTOpPack::ConstSubMultiVectorView< Scalar > *sub_mv) const =0
	Free a non-changeable explicit view of a sub-multi-vector. More...

virtual void	acquireNonconstDetachedMultiVectorViewImpl (const Range1D &rowRng, const Range1D &colRng, RTOpPack::SubMultiVectorView< Scalar > *sub_mv)=0
	Get a changeable explicit view of a sub-multi-vector. More...

virtual void	commitNonconstDetachedMultiVectorViewImpl (RTOpPack::SubMultiVectorView< Scalar > *sub_mv)=0
	Commit changes for a changeable explicit view of a sub-multi-vector. More...

virtual bool	rowStatIsSupportedImpl (const RowStatLinearOpBaseUtils::ERowStat rowStat) const

virtual void	getRowStatImpl (const RowStatLinearOpBaseUtils::ERowStat rowStat, const Ptr< VectorBase< Scalar > > &rowStatVec) const

virtual bool	supportsScaleLeftImpl () const

virtual bool	supportsScaleRightImpl () const

virtual void	scaleLeftImpl (const VectorBase< Scalar > &row_scaling)

virtual void	scaleRightImpl (const VectorBase< Scalar > &col_scaling)

Detailed Description

template<class Scalar>
class Thyra::MultiVectorBase< Scalar >

Interface for a collection of column vectors called a multi-vector.

Outline

Introduction

The primary purpose for this interface is to allow for the convenient aggregation of column vectors as a single matrix-like object. Such an orderly arrangement of column vectors into a single aggregate object allows for better optimized linear algebra operations such as matrix-matrix multiplication and the solution of linear systems for multiple right-hand sides. Every computing environment (serial, parallel, out-of-core etc.) should be able to define at least one reasonably efficient implementation of this interface.

Changeable and non-changeable views

This interface allows a client to create VectorBase and MultiVectorBase views of single and multiple columns of *this multi-vector, respectively. These two views are described separately in the next two subsections. The behavior of the vector and multi-vector views is very similar and the common behavior is described in the subsection Common behavior of vector and multi-vector views.

Accessing the individual columns as vector views

The individual columns of a multi-vector can be access using the non-const and const versions of the col() function. For example, the individual columns of one multi-vector can be copied to another as follows

template<class Scalar>
void copyOneColumnAtATime(
  const Thyra::MultiVectorBase<Scalar>   &X
  ,Thyra::MultiVectorBase<Scalar>        *Y
  )
{
  for( int j = =; j < X.domain()->dim(); ++j )
    assign( &*Y->col(j), *X.col(j) );
} 

In the above code fragment, the expression X.col(j) returns a smart-pointer to a non-changeable column of X while the expression Y->col(j) returns a smart-pointer to a changeable column of Y which is being modified.

Note: A modification to Y is not guaranteed to be committed back to Y until the smart pointer returned from Y.col(j) is deleted.

Accessing collections of columns as multi-vector views

Another important aspect of this interface is the ability to allow clients to access non-changeable and changeable MultiVectorBase views of columns of a parent MultiVectorBase object. These sub-views are created with one of the overloaded subView() functions of which there are two general forms.

The first form provides views of contiguous columns through the functions subView(const Range1D&) and subView(const Range1D&)const. For example, the following function shows how to copy the first three columns of one multi-vector to the last three columns of another multi-vector.

template<class Scalar>
void copyThreeColumns(
  const Thyra::MultiVectorBase<Scalar> &X
  ,Thyra::MultiVectorBase<Scalar>      *Y
  )
{
  const int m = Y->domain()->dim();
  assign( &*Y->subView(Range1D(m-3,m-1)), *X.subView(Range1D(0,2)) );
}

Note: In the above example *Y can be the same multi-vector as X.

Note: In the above example *Y is not guaranteed to be updated until the view returned from Y->subView(Range1D(m-3,m-1) is destroyed (which occurs at the end of the statement in which it occurs in this case).

The second form provides views of non-contiguous columns through the functions subView(const int numCols, const int cols[]) and subView(const int numCols, const int cols[]) const. For example, the following function copies columns 1, 3, and 5 from one multi-vector to columns 2, 4, and 6 of another multi-vector.

template<class Scalar>
void copyThreeStaggeredColumns(
  const Thyra::MultiVectorBase<Scalar> &X
  ,Thyra::MultiVectorBase<Scalar>      *Y
  )
{
  using Teuchos::tuple;
  assign( Y->subView(tuple<int>(2,4,6)()).ptr(), *X.subView(tuple<int>(1,3,5)()) );
}

Note: In the above example *Y can be the same multi-vector as X.

Note: In the above example *Y is not guaranteed to be updated until the view returned from Y->subView(tuple<int>(2,4,6)()) is destroyed (which occurs at the end of the statement in which it occurs in this case).

In general, the first contiguous form of views will be more efficient that the second non-contiguous form. Therefore, user's should try to structure their ANAs to use the contiguous form of multi-vector views if possible and only result to the non-contiguous form of views when absolutely needed.

Common behavior of vector and multi-vector views

When a view is created it may become a largely separate object from the parent multi-vector and the exact relationship between the two in undefined by this interface. This is true whether we are talking about individual column vector views or contiguous or non-contiguous multiple-column multi-vector views which are described above. These views and the parent multivector follow the state behavior outlined here.

If X_view is some view of a parent multi-vector X the following restrictions apply:

Undefined behavior: Changing the parent

The client should not attempt to change the parent multi-vector X while any view is active. The behavior of doing so is undefined. For example, the value returned from the following function and the final state of the parent multi-vector *X are undefined:

template<class Scalar>

Scalar undefinedBehaviorFromChangingParent(

Thyra::MultiVectorBase<Scalar> *X

)

{

// Create the view

RCP< Thyra::MultiVectorBase<Scalar> >

X_view = X->subView(Teuchos::Range1D(0,0));

// Change the parent while the view is still active

Teuchos::assign( X, Teuchos::ScalarTraits<Scalar>::one() );

// Above, changing the parent multi-vector may or may not change the subview

return Teuchos::norm_1(*X_view); // The value returned is undefined

// When the RCP X_view goes out of scope here, the state of the

// parent multi-vector *X is undefined!

}
Undefined behavior: Changing the view and accessing the parent while view is still active

The client should not attempt to change the view X_view and then access the parent multi-vector X while the view is still active. The behavior of doing so is undefined. For example, the value returned from the following function is undefined:

template<class Scalar>

Scalar undefinedBehaviorFromChaningViewAndAccessingParent(

Thyra::MultiVectorBase<Scalar> *X

)

{

// Create the view

RCP< Thyra::MultiVectorBase<Scalar> >

X_view = X->subView(Teuchos::Range1D(0,0));

// Change the view

Teuchos::assign( *&X_view, Teuchos::ScalarTraits<Scalar>::one() );

// Above, changing the view may or may not immediately update the parent multi-vector

return Teuchos::norm_1(*X); // The value returned from the parent is undefined at this point

// When the RCP X_view goes out of scope here, the parent multi-vector

// *X is guaranteed to be updated

}
Undefined behavior: Creating overlapping changeable views

The client should not attempt to create overlapping changeable views. If any of these changeable views is modified, the the behavior of the parent multi-vector is undefined. For example, the state of the parent multi-vector *X is undefined after the following function returns:

template<class Scalar>

Scalar undefinedBehaviorOfOverlappingViews(

Thyra::MultiVectorBase<Scalar> *X

)

{

// Create two overlapping views

RCP< Thyra::MultiVectorBase<Scalar> >

X_view1 = X->subView(Teuchos::Range1D(0,0)),

X_view2 = X->subView(Teuchos::Range1D(0,0));

// Change one of the views but not the other

Teuchos::assign( *&X_view2, Teuchos::ScalarTraits<Scalar>::one() );

// Once the RCPs X_view1 and X_view2 go out of scope here,

// the state of the parent multi-vector *X is undefined! In some cases,

// the intial view in X_view1 will be relected in X and in other

// cases the view in X_view2 will be written to the parent X.

}

Note that overlapping non-changeable views of a multi-vector are just fine since they do not change the state of the parent multi-vector.

In general, to stay out of trouble with multi-vector views:

Never change or access the parent multi-vector while a changeable view is active.
Never create simultaneous changeable overlapping views.

Note, however, that creating simultaneous non-overlapping non-changeable or changeable views is just fine as long as the parent multi-vector is not modified while the views are active. For example, the final state of *X is well defined after the following function finishes executing:

template<class Scalar>
Scalar wellDefinedBehaviorOfNonOverlappingViews(
  Thyra::MultiVectorBase<Scalar>   *X
  )
{
  // Create two non-overlapping views
  RCP< Thyra::MultiVectorBase<Scalar> >
    X_view1 = X->subView(Teuchos::Range1D(0,0)),
    X_view2 = X->subView(Teuchos::Range1D(1,1));
  // Change the two views
  Teuchos::assign( *&X_view1, Teuchos::ScalarTraits<Scalar>::zero() );
  Teuchos::assign( *&X_view2, Teuchos::ScalarTraits<Scalar>::one() );
  // When the RCPs X_view1 and X_view2 go out of scope here,
  // the state of the parent multi-vector *X will be guaranteed to be
  // updated to the values changed in these views.
} 

MultiVectorBase as a linear operator

The MultiVectorBase interface is derived from the LinearOpBase interface and therefore every MultiVectorBase object can be used as a linear operator which has some interesting implications. Since a linear operator can apply itself to vectors and multi-vectors and a multi-vector is a linear operator, this means that a multi-vector can apply itself to other vectors and multi-vectors. There are several different use cases that this functionality is useful. Two of the more important use cases are block updates and block inner products.

Multi-vector block updates

Let V and Y be multi-vector objects with the same vector space with a very large number of rows m and a moderate number of columns n. Now, consider the block update of the form

  Y = Y + V * B

where the multi-vector B is of dimension n x b.

The following function shows how this block update might be performed.

template<class Scalar>
void myBlockUpdate(
  const Thyra::MultiVectorBase<Scalar> &V
  ,const int                           b
  ,Thyra::MultiVectorBase<Scalar>      *Y
  )
{
  typedef Teuchos::ScalarTraits<Scalar> ST;
  // Create the multi-vector B used for the update
  RCP<Thyra::MultiVectorBase<Scalar> >
    B = createMembers(V.domain(),b);
  // Fill up B for the update
  ...
  // Do the update Y = V*B + Y
  V.apply(Thyra::NONCONJ_ELE,*B,Y,ST::one(),ST::one());
}

In a block update, as demonstrated above, level-3 BLAS can be used to provide a very high level of performance. Note that in an SPMD program, that B would be a locally replicated multi-vector and V and Y would be distributed-memory multi-vectors. In an SPMD environment, there would be no global communication in a block update.

Multi-vector block inner products

An important operation supported by the LinearOpBase::applyTranspose() function is the block inner product which takes the form

  B = adjoint(V)*X

where V and X are tall, thin multi-vectors and B is a small multi-vector. In an SPMD environment, V and X would be distributed-memory objects while B would be locally replicated in each process. The following function shows how block inner product would be performed:

template<class Scalar>
RCP<Thyra::MultiVectorBase<Scalar> >
void myBlockInnerProd(
  const Thyra::MultiVectorBase<Scalar>                    &V
  ,const Thyra::MultiVectorBase<Scalar>                   &X
  )
{
  // Create the multi-vector B used for the result
  RCP<Thyra::MultiVectorBase<Scalar> >
    B = createMembers(V.domain(),X.domain()->dim());
  // Do the inner product B = adjoint(V)*X
  V.applyTranspose(Thyra::CONJ_ELE,X,&*B);
  // Return the result
  return B;
}

In an SPMD program, the above block inner product will use level-3 BLAS to multiply the local elements of V and X and will then do a single global reduction to assemble the product B in all of the processes.

Support for reduction/transformation operations

Another powerful feature of this interface is the ability to apply reduction/transformation operators over a sub-set of rows and columns in a set of multi-vector objects using the applyOp() functions. The behavior is identical to the client extracting each column in a set of multi-vectors and calling VectorBase::applyOp() individually on these columns. However, the advantage of using the multi-vector apply functions is that there may be greater opportunities for increased performance in a number of respects. Also, the intermediate reduction objects over a set of columns can be reduced by a secondary reduction object.

Collection of pre-written RTOps and wrapper functions

There already exists RTOp-based implementations of several standard vector operations and some convenience functions that wrap these operators and call applyOp(). See the Operator/Vector Support Software collection for these.

Explicit multi-vector coefficient access

This interface also allows a client to extract a sub-set of elements in an explicit form as non-changeable RTOpPack::ConstSubMultiVectorView objects or changeable RTOpPack::SubMultiVectorView objects using the acquireDetachedView() functions. In general, this is a very bad thing to do and should be avoided. However, there are some situations where this is needed, just as is the case for vectors (see Explicit vector coefficient access). The default implementation of these explicit access functions use sophisticated reduction/transformation operators with the applyOp() function in order to extract and set the needed elements. Therefore, all MultiVectorBase subclasses automatically support these operations (even if it is a bad idea to use them).

Explicit multi-vector coefficient access utilities

Client code in general should not directly call the above described explicit sub-multi-vector access functions but should instead use the utility classes ConstDetachedMultiVectorView and DetachedMultiVectorView since these are easier to use and safer in the event that an exception is thrown. These classes are documented in the Operator/Vector Support Software collection.

Notes for subclass developers

This is a fairly bare-bones interface class without much in the way of default function implementations. The subclass MultiVectorDefaultBase (contained in the Operator/Vector Support Software collection) uses a default multi-vector implementation to provide overrides of many of the functions and should be the first choice for subclasses implementations to derive their implementations from rather than starting from scratch.

Definition at line 461 of file Thyra_MultiVectorBase_decl.hpp.

Member Function Documentation

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::assign ( Scalar alpha )

inline

V = alpha.

Parameters

alpha [in] Scalar that is assigned to all multi-vector coefficients.

NVI function.

Definition at line 481 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::assign ( const MultiVectorBase< Scalar > & mv )

inline

V = mv.

Parameters

mv	[in] Multi-vector whose value is assigned to this multi-vector

NVI function.

Definition at line 491 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::scale ( Scalar alpha )

inline

V = alpha*V.

Parameters

alpha [in] Scaling factor.

NVI function.

Definition at line 500 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::update	(	Scalar	alpha,
		const MultiVectorBase< Scalar > &	mv
	)

inline

V = alpha*mv + V.

Parameters

alpha	[in] Scaling factor for input mv.
mv	[in] Multi-vector to be added to this multi-vector.

NVI function.

Definition at line 511 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::linear_combination	(	const ArrayView< const Scalar > &	alpha,
		const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &	mv,
		const Scalar &	beta
	)

inline

Y.col(j)(i) = beta*Y.col(j)(i) + sum( alpha[k]*X[k].col(j)(i),

k=0...m-1 ), for i = 0...Y->range()->dim()-1, j = 0...Y->domain()->dim()-1.

Parameters

alpha	[in] Array (length `m`) of input scalars.
X	[in] Array (length `m`) of input multi-vectors.
beta	[in] Scalar multiplier for Y
Y	[in/out] Target multi-vector that is the result of the linear combination.

This function implements a general linear combination:

Y.col(j)(i) = beta*Y.col(j)(i) + alpha[0]*X[0].col(j)(i) + alpha[1]*X[1].col(j)(i) + ... + alpha[m-1]*X[m-1].col(j)(i)

   for:
       i = 0...y->space()->dim()-1
       j = 0...y->domain()->dim()-1

NVI function.

Definition at line 542 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::dots	(	const MultiVectorBase< Scalar > &	mv,
		const ArrayView< Scalar > &	prods
	)		const

inline

Column-wise Euclidean dot product.

Parameters

V	[in] Multi-vector with which to take the dot product.
prods	[out] Array (size `m = this->domain()->dim()`) of dot prods `prods[j] = dot(*mv.col(j))`, for `j=0...m-1`.

NVI function.

Definition at line 558 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::norms_1 ( const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > & norms ) const

inline

Column-wise 1-norms.

Parameters

norms [out] Array (size m = this->domain()->dim()) of 1-norms norms[j] = norm_1(this->col(j)), for j=0...m-1.

NVI function.

Definition at line 571 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::norms_2 ( const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > & norms ) const

inline

Column-wise 2-norms.

Parameters

norms [out] Array (size m = this->domain()->dim()) of 2-norms norms[j] = norm_2(this->col(j)), for j=0...m-1.

NVI function.

Definition at line 583 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::norms_inf ( const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > & norms ) const

inline

Column-wise infinity-norms.

Parameters

norms [out] Array (size m = this->domain()->dim()) of inf-norms norms[j] = norm_inf(this->col(j)), for j=0...m-1.

NVI function.

Definition at line 595 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

RCP<const VectorBase<Scalar> > Thyra::MultiVectorBase< Scalar >::col ( Ordinal j ) const

inline

Calls colImpl().

Temporary NVI function.

Definition at line 609 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

RCP<VectorBase<Scalar> > Thyra::MultiVectorBase< Scalar >::col ( Ordinal j )

inline

Calls nonconstColImpl().

Temporary NVI function.

Definition at line 616 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

RCP<const MultiVectorBase<Scalar> > Thyra::MultiVectorBase< Scalar >::subView ( const Range1D & colRng ) const

inline

Calls contigSubViewImpl().

Temporary NVI function.

Definition at line 629 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

RCP<MultiVectorBase<Scalar> > Thyra::MultiVectorBase< Scalar >::subView ( const Range1D & colRng )

inline

Calls nonconstContigSubViewImpl().

Temporary NVI function.

Definition at line 639 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

RCP<const MultiVectorBase<Scalar> > Thyra::MultiVectorBase< Scalar >::subView ( const ArrayView< const int > & cols ) const

inline

nonContigSubViewImpl().

Temporary NVI function.

Definition at line 647 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

RCP<MultiVectorBase<Scalar> > Thyra::MultiVectorBase< Scalar >::subView ( const ArrayView< const int > & cols )

inline

nonconstNonContigSubViewImpl().

Temporary NVI function.

Definition at line 655 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::applyOp	(	const RTOpPack::RTOpT< Scalar > &	primary_op,
		const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &	multi_vecs,
		const ArrayView< const Ptr< MultiVectorBase< Scalar > > > &	targ_multi_vecs,
		const ArrayView< const Ptr< RTOpPack::ReductTarget > > &	reduct_objs,
		const Ordinal	primary_global_offset
	)		const

inline

Calls mvMultiReductApplyOpImpl().

Temporary NVI function.

Definition at line 667 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::applyOp	(	const RTOpPack::RTOpT< Scalar > &	primary_op,
		const RTOpPack::RTOpT< Scalar > &	secondary_op,
		const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &	multi_vecs,
		const ArrayView< const Ptr< MultiVectorBase< Scalar > > > &	targ_multi_vecs,
		const Ptr< RTOpPack::ReductTarget > &	reduct_obj,
		const Ordinal	primary_global_offset
	)		const

inline

mvSingleReductApplyOpImpl().

Temporary NVI function.

Definition at line 683 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::acquireDetachedView	(	const Range1D &	rowRng,
		const Range1D &	colRng,
		RTOpPack::ConstSubMultiVectorView< Scalar > *	sub_mv
	)		const

inline

Calls acquireDetachedMultiVectorViewImpl().

Temporary NVI function.

Definition at line 705 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::releaseDetachedView ( RTOpPack::ConstSubMultiVectorView< Scalar > * sub_mv ) const

inline

Calls releaseDetachedMultiVectorViewImpl().

Temporary NVI function.

Definition at line 716 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::acquireDetachedView	(	const Range1D &	rowRng,
		const Range1D &	colRng,
		RTOpPack::SubMultiVectorView< Scalar > *	sub_mv
	)

inline

Calls acquireNonconstDetachedMultiVectorViewImpl().

Temporary NVI function.

Definition at line 725 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

void Thyra::MultiVectorBase< Scalar >::commitDetachedView ( RTOpPack::SubMultiVectorView< Scalar > * sub_mv )

inline

Calls commitNonconstDetachedMultiVectorViewImpl().

Temporary NVI function.

Definition at line 736 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar>

virtual RCP<MultiVectorBase<Scalar> > Thyra::MultiVectorBase< Scalar >::clone_mv ( ) const

pure virtual

Clone the multi-vector object (if supported).

The default implementation uses the vector space to create a new multi-vector object and then uses a transformation operator to assign the vector elements. A subclass should only override this function if it can do something more sophisticated (i.e. lazy evaluation) but in general, this is not needed.

Implemented in Thyra::DefaultProductMultiVector< Scalar >, Thyra::VectorDefaultBase< Scalar >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar >

RCP< const LinearOpBase< Scalar > > Thyra::MultiVectorBase< Scalar >::clone ( ) const

virtual

This function is simply overridden to return this->clone_mv().

Reimplemented from Thyra::LinearOpBase< Scalar >.

Definition at line 39 of file Thyra_MultiVectorBase_def.hpp.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::assignImpl ( Scalar alpha )

protectedpure virtual

Virtual implementation for NVI assign(Scalar).

Implemented in Thyra::DefaultProductVector< Scalar >, Thyra::DefaultMultiVectorProductVector< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::TpetraVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultProductMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::assignMultiVecImpl ( const MultiVectorBase< Scalar > & mv )

protectedpure virtual

Virtual implementation for NVI assign(MV).

Implemented in Thyra::DefaultProductVector< Scalar >, Thyra::DefaultMultiVectorProductVector< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::TpetraVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultProductMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::scaleImpl ( Scalar alpha )

protectedpure virtual

Virtual implementation for NVI scale().

Implemented in Thyra::DefaultProductVector< Scalar >, Thyra::DefaultMultiVectorProductVector< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::TpetraVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultProductMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::updateImpl	(	Scalar	alpha,
		const MultiVectorBase< Scalar > &	mv
	)

protectedpure virtual

Virtual implementation for NVI update().

Implemented in Thyra::DefaultProductVector< Scalar >, Thyra::DefaultMultiVectorProductVector< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::TpetraVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultProductMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::linearCombinationImpl	(	const ArrayView< const Scalar > &	alpha,
		const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &	mv,
		const Scalar &	beta
	)

protectedpure virtual

Virtual implementation for NVI linear_combination().

Implemented in Thyra::DefaultProductVector< Scalar >, Thyra::DefaultMultiVectorProductVector< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::TpetraVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultProductMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::dotsImpl	(	const MultiVectorBase< Scalar > &	mv,
		const ArrayView< Scalar > &	prods
	)		const

protectedpure virtual

Virtual implementation for NVI dots().

Implemented in Thyra::DefaultProductVector< Scalar >, Thyra::DefaultMultiVectorProductVector< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::TpetraVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultProductMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::norms1Impl ( const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > & norms ) const

protectedpure virtual

Virtual implementation for NVI norms_1().

Implemented in Thyra::DefaultProductVector< Scalar >, Thyra::DefaultMultiVectorProductVector< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::TpetraVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultProductMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::norms2Impl ( const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > & norms ) const

protectedpure virtual

Virtual implementation for NVI norms_2().

Implemented in Thyra::DefaultProductVector< Scalar >, Thyra::DefaultMultiVectorProductVector< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::TpetraVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultProductMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::normsInfImpl ( const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > & norms ) const

protectedpure virtual

Virtual implementation for NVI norms_inf().

Implemented in Thyra::DefaultProductVector< Scalar >, Thyra::DefaultMultiVectorProductVector< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::TpetraVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::DefaultProductMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar >

RCP< const VectorBase< Scalar > > Thyra::MultiVectorBase< Scalar >::colImpl ( Ordinal j ) const

protectedvirtual

Return a non-changeable view of a constituent column vector.

Parameters

j	[in] zero-based index of the column to return a view for

Preconditions:

this->domain().get()!=NULL && this->range().get()!=NULL (throw std::logic_error)
0 <= j && j < this->domain()->dim() (throw std::invalid_argument)

Postconditions:

return.get() != NULL
this->range()->isCompatible(*return->space()) == true

See Accessing the individual columns as vector views and Common behavior of vector and multi-vector views for the behavior of this view.

The default implementation of this function (which is the only implementation needed by most subclasses) is based on the non-const version col().

Reimplemented in Thyra::DefaultProductMultiVector< Scalar >, and Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >.

Definition at line 28 of file Thyra_MultiVectorBase_def.hpp.

template<class Scalar>

virtual RCP<VectorBase<Scalar> > Thyra::MultiVectorBase< Scalar >::nonconstColImpl ( Ordinal j )

protectedpure virtual

Return a changeable view of a constituent column vector.

Parameters

j	[in] zero-based index of the column to return a view for

Preconditions:

this->domain().get()!=NULL && this->range().get()!=NULL (throw std::logic_error)
0 <= j && j < this->domain()->dim() (throw std::invalid_argument)

Postconditions:

return.get() != NULL
this->range()->isCompatible(*return->space()) == true

See Accessing the individual columns as vector views and Common behavior of vector and multi-vector views for the behavior of this view.

Note: *this is not guaranteed to be modified until the smart pointer returned by this function is destroyed.

Implemented in Thyra::DefaultProductMultiVector< Scalar >, Thyra::VectorDefaultBase< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::DefaultSpmdMultiVector< Scalar >, and Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >.

template<class Scalar>

virtual RCP<const MultiVectorBase<Scalar> > Thyra::MultiVectorBase< Scalar >::contigSubViewImpl ( const Range1D & colRng ) const

protectedpure virtual

Return a non-changeable sub-view of a contiguous set of columns of the this multi-vector.

Parameters

colRng [in] zero-based range of columns to create a view of. Note that it is valid for colRng.full_range()==true in which case the view of the entire multi-vector is taken.

Preconditions:

this->domain().get()!=NULL && this->range().get()!=NULL (throw std::logic_error)
[!colRng.full_range()] colRng.ubound() < this->domain()->dim() (throw std::invalid_argument)

Postconditions:

this->range()->isCompatible(*return->range()) == true
return->domain()->dim() == Teuchos::full_range(colRng,0,this->domain()->dim()-1).size()
*return->col(k) represents the same column vector as this->col(colRng.lbound()+k), for k=0...Teuchos::full_range(colRng,0,this->domain()->dim()).ubound()-1

See Accessing collections of columns as multi-vector views and Common behavior of vector and multi-vector views for the behavior of this view.

Implemented in Thyra::DefaultProductMultiVector< Scalar >, Thyra::VectorDefaultBase< Scalar >, Thyra::DefaultSpmdMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual RCP<MultiVectorBase<Scalar> > Thyra::MultiVectorBase< Scalar >::nonconstContigSubViewImpl ( const Range1D & colRng )

protectedpure virtual

Return a changeable sub-view of a contiguous set of columns of the this multi-vector.

Parameters

colRng [in] zero-based range of columns to create a view of. Note that it is valid for colRng.full_range()==true in which case the view of the entire multi-vector is taken.

Preconditions:

this->domain().get()!=NULL && this->range().get()!=NULL (throw std::logic_error)
[!colRng.full_range()] colRng.ubound() < this->domain()->dim() (throw std::invalid_argument)

Postconditions:

this->range()->isCompatible(*return->range()) == true
return->domain()->dim() == Teuchos::full_range(colRng,0,this->domain()->dim()-1).size()
*return->col(k) represents the same column vector as this->col(colRng.lbound()+k), for k=0...Teuchos::full_range(colRng,0,this->domain()->dim()).ubound()-1

See Accessing collections of columns as multi-vector views and Common behavior of vector and multi-vector views for the behavior of this view.

Implemented in Thyra::DefaultProductMultiVector< Scalar >, Thyra::VectorDefaultBase< Scalar >, Thyra::DefaultColumnwiseMultiVector< Scalar >, Thyra::DefaultSpmdMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual RCP<const MultiVectorBase<Scalar> > Thyra::MultiVectorBase< Scalar >::nonContigSubViewImpl ( const ArrayView< const int > & cols ) const

protectedpure virtual

Return a non-changeable sub-view of a non-contiguous set of columns of this multi-vector.

Parameters

cols	[in] Array of the zero-based column indexes to use in the returned view.

Preconditions:

this->domain().get()!=NULL && this->range().get()!=NULL (throw std::logic_error)
cols.size() <= this->domain()->dim() (throw std::invalid_argument)
0 <= cols[k] < this->domain()->dim(), for k=0...cols.size()-1 (throw std::invalid_argument)
col[k1] != col[k2], for all k1 != k2 in the range [0,cols.size()-1]

Postconditions:

this->range()->isCompatible(*return->range()) == true
return->domain()->dim() == cols.size()
*return->col(k) represents the same column vector as this->col(cols[k]), for k=0...cols.size()-1

See Accessing collections of columns as multi-vector views and Common behavior of vector and multi-vector views for the behavior of this view.

Implemented in Thyra::DefaultProductMultiVector< Scalar >, Thyra::VectorDefaultBase< Scalar >, Thyra::DefaultSpmdMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual RCP<MultiVectorBase<Scalar> > Thyra::MultiVectorBase< Scalar >::nonconstNonContigSubViewImpl ( const ArrayView< const int > & cols )

protectedpure virtual

Return a changeable sub-view of a non-contiguous set of columns of this multi-vector.

Parameters

cols	[in] Array of the zero-based column indexes to use in the returned view.

Preconditions:

this->domain().get()!=NULL && this->range().get()!=NULL (throw std::logic_error)
cols.size() <= this->domain()->dim() (throw std::invalid_argument)
0 <= cols[k] < this->domain()->dim(), for k=0...cols.size()-1 (throw std::invalid_argument)
col[k1] != col[k2], for all k1 != k2 in the range [0,cols.size()-1]

Postconditions:

this->range()->isCompatible(*return->range()) == true
return->domain()->dim() == cols.size()
*return->col(k) represents the same column vector as this->col(cols[k]), for k=0...cols.size()-1

See Accessing collections of columns as multi-vector views and Common behavior of vector and multi-vector views for the behavior of this view.

Implemented in Thyra::DefaultProductMultiVector< Scalar >, Thyra::VectorDefaultBase< Scalar >, Thyra::DefaultSpmdMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::mvMultiReductApplyOpImpl	(	const RTOpPack::RTOpT< Scalar > &	primary_op,
		const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &	multi_vecs,
		const ArrayView< const Ptr< MultiVectorBase< Scalar > > > &	targ_multi_vecs,
		const ArrayView< const Ptr< RTOpPack::ReductTarget > > &	reduct_objs,
		const Ordinal	primary_global_offset
	)		const

protectedpure virtual

Apply a reduction/transformation operator column by column and return an array of the reduction objects.

Preconditions:

this->domain().get()!=NULL && this->range().get()!=NULL (throw std::logic_error)
See the preconditions for Thyra::applyOp()

See the documentation for the function Thyra::applyOp() for a description of the arguments.

This function is not to be called directly by the client but instead through the nonmember function Thyra::applyOp().

It is expected that this will be one of the multi-vector objects in multi_vecs[] or targ_multi_vecs[].

The default implementation calls VectorBase::applyOp() on each column this->col(j) for j = 0 ... this->range()->dim()-1.

Implemented in Thyra::DefaultProductMultiVector< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Thyra::MultiVectorDefaultBase< Scalar >, and Thyra::SpmdMultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::mvSingleReductApplyOpImpl	(	const RTOpPack::RTOpT< Scalar > &	primary_op,
		const RTOpPack::RTOpT< Scalar > &	secondary_op,
		const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &	multi_vecs,
		const ArrayView< const Ptr< MultiVectorBase< Scalar > > > &	targ_multi_vecs,
		const Ptr< RTOpPack::ReductTarget > &	reduct_obj,
		const Ordinal	primary_global_offset
	)		const

protectedpure virtual

Apply a reduction/transformation operator column by column and reduce the intermediate reduction objects into a single reduction object.

Preconditions:

this->domain().get()!=NULL && this->range().get()!=NULL (throw std::logic_error)
See the preconditions for Thyra::applyOp()

See the documentation for the function Thyra::applyOp() for a description of the arguments.

This function is not to be called directly by the client but instead through the nonmember function Thyra::applyOp().

It is expected that this will be one of the multi-vector objects in multi_vecs[] or targ_multi_vecs[].

The default implementation calls applyOp() where an array of reduction objects is taken.

Implemented in Thyra::MultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::acquireDetachedMultiVectorViewImpl	(	const Range1D &	rowRng,
		const Range1D &	colRng,
		RTOpPack::ConstSubMultiVectorView< Scalar > *	sub_mv
	)		const

protectedpure virtual

Get a non-changeable explicit view of a sub-multi-vector.

Parameters

rowRng	[in] The range of the rows to extract the sub-multi-vector view.
colRng	[in] The range of the columns to extract the sub-multi-vector view.
sub_mv	[in/out] View of the sub-multi_vector. Prior to the first call to this function, `sub_mv->set_uninitialized()` must be called. Technically `*sub_mv` owns the memory but this memory can be freed only by calling `this->releaseDetachedView(sub_mv)`.

Preconditions:

this->range().get()!=NULL && this->domain().get()!=NULL (throw std::logic_error)
[!rowRng.full_range()] rowRng.ubound() < this->range()->dim() (throw std::out_of_range)
[!colRng.full_range()] colRng.ubound() < this->domain()->dim() (throw std::out_of_range)

Postconditions:

*sub_mv contains an explicit non-changeable view to the elements in the row and column ranges Teuchos::full_range(rowRng,0,this->range()->dim()-1) and Teuchos::full_range(colRng,0,this->domain()->dim()-1) respectively.

Note: This view is to be used immediately and then released with a call to releaseDetachedView().

Note that calling this operation might require some dynamic memory allocations and temporary memory. Therefore, it is critical that this->releaseDetachedView(sub_mv) be called by client in order to clean up memory and avoid memory leaks after the sub-multi-vector view is finished being used.

Heads Up! Note that client code in general should not directly call this function but should instead use the utility class ConstDetachedMultiVectorView which will also take care of calling releaseDetachedView().

If this->acquireDetachedView(...,sub_mv) was previously called on sub_mv then it may be possible to reuse this memory if it is sufficiently sized. The user is encouraged to make multiple calls to this->acquireDetachedView(...,sub_mv) before this->releaseDetachedView(sub_mv) to finally clean up all of the memory. Of course, the same sub_mv object must be passed to the same multi-vector object for this to work correctly.

This function has a default implementation based on the vector operation VectorBase::acquireDetachedView() called on the non-changeable vector objects returned from col(). Note that the footprint of the reduction object (both internal and external state) will be O(rowRng.size()*colRng.size()). For serial applications this is fairly reasonable and will not be a major performance penalty. For parallel applications, however, this is a terrible implementation and must be overridden if rowRng.size() is large at all. Although, this function should not even be used in cases where the multi-vector is very large. If a subclass does override this function, it must also override releaseDetachedView() which has a default implementation which is a companion to this function's default implementation.

Implemented in Thyra::DefaultProductMultiVector< Scalar >, Thyra::VectorDefaultBase< Scalar >, Thyra::MultiVectorDefaultBase< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::SpmdMultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::releaseDetachedMultiVectorViewImpl ( RTOpPack::ConstSubMultiVectorView< Scalar > * sub_mv ) const

protectedpure virtual

Free a non-changeable explicit view of a sub-multi-vector.

Parameters

sub_mv * [in/out] The memory referred to by sub_mv->values() * will be released if it was allocated and *sub_mv will be zeroed out using sub_mv->set_uninitialized().

Preconditions:

this->range().get()!=NULL && this->domain().get()!=NULL (throw std::logic_error)
sub_mv must have been passed through a call to this->acquireDetachedView(...,sub_mv)

Postconditions:

See RTOpPack::ConstSubMultiVectorView::set_uninitialized() for sub_mv

The sub-multi-vector view must have been allocated by this->acquireDetachedView() first.

This function has a default implementation which is a companion to the default implementation for acquireDetachedView(). If acquireDetachedView() is overridden by a subclass then this function must be overridden also!

Implemented in Thyra::DefaultProductMultiVector< Scalar >, Thyra::VectorDefaultBase< Scalar >, Thyra::MultiVectorDefaultBase< Scalar >, and Thyra::SpmdMultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::acquireNonconstDetachedMultiVectorViewImpl	(	const Range1D &	rowRng,
		const Range1D &	colRng,
		RTOpPack::SubMultiVectorView< Scalar > *	sub_mv
	)

protectedpure virtual

Get a changeable explicit view of a sub-multi-vector.

Parameters

rowRng	[in] The range of the rows to extract the sub-multi-vector view.
colRng	[in] The range of the columns to extract the sub-multi-vector view.
sub_mv	[in/out] Changeable view of the sub-multi-vector. Prior to the first call `sub_mv->set_uninitialized()` must have been called for the correct behavior. Technically `*sub_mv` owns the memory but this memory must be committed and freed only by calling `this->commitDetachedView(sub_mv)`.

Preconditions:

this->range().get()!=NULL && this->domain().get()!=NULL (throw std::logic_error)
[!rowRng.full_range()] rowRng.ubound() < this->range()->dim() (throw std::out_of_range)
[!colRng.full_range()] colRng.ubound() < this->domain()->dim() (throw std::out_of_range)

Postconditions:

*sub_mv contains an explicit changeable view to the elements in the row and column ranges full_range(rowRng,0,this->range()->dim()-1) and full_range(colRng,0,this->domain()->dim()-1) respectively.

Note: This view is to be used immediately and then committed back with a call to commitDetachedView().

Note that calling this operation might require some internal allocations and temporary memory. Therefore, it is critical that this->commitDetachedView(sub_mv) is called to commit the changed entries and clean up memory and avoid memory leaks after the sub-multi-vector is modified.

Heads Up! Note that client code in general should not directly call this function but should instead use the utility class DetachedMultiVectorView which will also take care of calling commitDetachedView.

If this->acquireDetachedView(...,sub_mv) was previously called on sub_mv then it may be possible to reuse this memory if it is sufficiently sized. The user is encouraged to make multiple calls to this->acquireDetachedView(...,sub_mv) before this->commitDetachedView(sub_mv) to finally clean up all of the memory. Of course the same sub_mv object must be passed to the same multi-vector object for this to work correctly.

Changes to the underlying sub-multi-vector are not guaranteed to become permanent until this->acquireDetachedView(...,sub_mv) is called again, or this->commitDetachedView(sub_mv) is called.

This function has a default implementation based on the vector operation VectorBase::acquireDetachedView() called on the changeable vector objects returned from col(). Note that the footprint of the reduction object (both internal and external state) will be O(rowRng.size()*colRng.size()). For serial applications this is fairly reasonable and will not be a major performance penalty. For parallel applications, however, this is a terrible implementation and must be overridden if rowRng.size() is large at all. Although, this function should not even be used in case where the multi-vector is very large. If a subclass does override this function, it must also override commitDetachedView() which has a default implementation which is a companion to this function's default implementation.

Implemented in Thyra::DefaultProductMultiVector< Scalar >, Thyra::MultiVectorDefaultBase< Scalar >, Thyra::VectorDefaultBase< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::SpmdMultiVectorDefaultBase< Scalar >.

template<class Scalar>

virtual void Thyra::MultiVectorBase< Scalar >::commitNonconstDetachedMultiVectorViewImpl ( RTOpPack::SubMultiVectorView< Scalar > * sub_mv )

protectedpure virtual

Commit changes for a changeable explicit view of a sub-multi-vector.

Parameters

sub_mv * [in/out] The data in sub_mv->values() will be written back to internal storage and the memory referred to by sub_mv->values() will be released if it was allocated * and *sub_mv will be zeroed out using * sub_mv->set_uninitialized().

Preconditions:

this->range().get()!=NULL && this->domain().get()!=NULL (throw std::logic_error)
sub_mv must have been passed through a call to this->acquireDetachedView(...,sub_mv)

Postconditions:

See RTOpPack::SubMultiVectorView::set_uninitialized() for sub_mv
*this will be updated according the the changes made to sub_mv

The sub-multi-vector view must have been allocated by this->acquireDetachedView() first.

This function has a default implementation which is a companion to the default implementation for acquireDetachedView(). If acquireDetachedView() is overridden by a subclass then this function must be overridden also!

Implemented in Thyra::MultiVectorDefaultBase< Scalar >, Thyra::DefaultProductMultiVector< Scalar >, Thyra::VectorDefaultBase< Scalar >, Thyra::TpetraMultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Thyra::SpmdMultiVectorDefaultBase< Scalar >.

template<class Scalar >

bool Thyra::MultiVectorBase< Scalar >::rowStatIsSupportedImpl ( const RowStatLinearOpBaseUtils::ERowStat rowStat ) const

protectedvirtual

From RowStatLinearOpBase

Implements Thyra::RowStatLinearOpBase< Scalar >.

Definition at line 48 of file Thyra_MultiVectorBase_def.hpp.

template<class Scalar >

void Thyra::MultiVectorBase< Scalar >::getRowStatImpl	(	const RowStatLinearOpBaseUtils::ERowStat	rowStat,
		const Ptr< VectorBase< Scalar > > &	rowStatVec
	)		const

protectedvirtual

From RowStatLinearOpBase

Implements Thyra::RowStatLinearOpBase< Scalar >.

Definition at line 65 of file Thyra_MultiVectorBase_def.hpp.

template<class Scalar >

bool Thyra::MultiVectorBase< Scalar >::supportsScaleLeftImpl ( ) const

protectedvirtual

From ScaledLinearOpBase

Implements Thyra::ScaledLinearOpBase< Scalar >.

Definition at line 94 of file Thyra_MultiVectorBase_def.hpp.

template<class Scalar >

bool Thyra::MultiVectorBase< Scalar >::supportsScaleRightImpl ( ) const

protectedvirtual

From ScaledLinearOpBase

Implements Thyra::ScaledLinearOpBase< Scalar >.

Definition at line 101 of file Thyra_MultiVectorBase_def.hpp.

template<class Scalar >

void Thyra::MultiVectorBase< Scalar >::scaleLeftImpl ( const VectorBase< Scalar > & row_scaling )

protectedvirtual

From ScaledLinearOpBase

Implements Thyra::ScaledLinearOpBase< Scalar >.

Definition at line 108 of file Thyra_MultiVectorBase_def.hpp.

template<class Scalar >

void Thyra::MultiVectorBase< Scalar >::scaleRightImpl ( const VectorBase< Scalar > & col_scaling )

protectedvirtual

From ScaledLinearOpBase

Implements Thyra::ScaledLinearOpBase< Scalar >.

Definition at line 117 of file Thyra_MultiVectorBase_def.hpp.

template<class Scalar >

void Thyra::MultiVectorBase< Scalar >::absRowSum ( const Teuchos::Ptr< Thyra::VectorBase< Scalar > > & output ) const

protected

Compute the absolute row sum of this multivector. Note that the implementation is suboptimal in that it requires an intermediate step of computing the absolute value of the multivector, then a "apply" operation by the rows.

Parameters

[out] output A vector constructed from the range vector space.

Definition at line 138 of file Thyra_MultiVectorBase_def.hpp.

template<class Scalar >

void Thyra::MultiVectorBase< Scalar >::absColSum ( const Teuchos::Ptr< Thyra::VectorBase< Scalar > > & output ) const

protected

Compute the absolute column sum of this multivector. Note that the implementation uses the norms_1 function.

Parameters

[out] output A vector constructed from the domain vector space.

Definition at line 157 of file Thyra_MultiVectorBase_def.hpp.

Friends And Related Function Documentation

template<class Scalar >

void applyOp	(	const RTOpPack::RTOpT< Scalar > &	primary_op,
		const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &	multi_vecs,
		const ArrayView< const Ptr< MultiVectorBase< Scalar > > > &	targ_multi_vecs,
		const ArrayView< const Ptr< RTOpPack::ReductTarget > > &	reduct_objs,
		const Ordinal	primary_global_offset = `0`
	)

ToDo: Finish documentation!

Definition at line 1309 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar >

void applyOp	(	const RTOpPack::RTOpT< Scalar > &	primary_op,
		const RTOpPack::RTOpT< Scalar > &	secondary_op,
		const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &	multi_vecs,
		const ArrayView< const Ptr< MultiVectorBase< Scalar > > > &	targ_multi_vecs,
		const Ptr< RTOpPack::ReductTarget > &	reduct_obj,
		const Ordinal	primary_global_offset = `0`
	)

ToDo: Finish documentation!

Definition at line 1335 of file Thyra_MultiVectorBase_decl.hpp.

template<class Scalar >

void norms	(	const MultiVectorBase< Scalar > &	V,
		const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &	norms
	)

Parameters

V	[in]
norms	[out] Array (size `m = V1->domain()->dim()`) of the natural norms `dot[j] = sqrt(scalarProd(V.col(j),V.col(j)))`, for `j=0...m-1`, computed using a single reduction.

template<class Scalar , class NormOp >

void reductions	(	const MultiVectorBase< Scalar > &	V,
		const NormOp &	op,
		const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &	norms
	)

Parameters

V	[in]
normOp	[in] A reduction operator consistent with the interface to `RTOpPack::ROpScalarReductionBase` that defines the norm operation.
norms	[out] Array (size `m = V1->domain()->dim()`) of one-norms `dot[j] = {some norm}(*V.col(j))`, for `j=0...m-1`, computed using a single reduction.

template<class Scalar >

void norms_1	(	const MultiVectorBase< Scalar > &	V,
		const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &	norms
	)

Parameters

V	[in]
norms	[out] Array (size `m = V1->domain()->dim()`) of one-norms `dot[j] = norm_1(*V.col(j))`, for `j=0...m-1`, computed using a single reduction.

template<class Scalar >

void norms_2	(	const MultiVectorBase< Scalar > &	V,
		const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &	norms
	)

Parameters

V	[in]
norms	[out] Array (size `m = V1->domain()->dim()`) of one-norms `dot[j] = norm_2(*V.col(j))`, for `j=0...m-1`, computed using a single reduction.

template<class Scalar >

void norms_inf	(	const MultiVectorBase< Scalar > &	V,
		const ArrayView< typename ScalarTraits< Scalar >::magnitudeType > &	norms
	)

Parameters

V	[in]
norms	[out] Array (size `m = V1->domain()->dim()`) of one-norms `dot[j] = norm_inf(*V.col(j))`, for `j=0...m-1`, computed using a single reduction.

template<class Scalar >

Array< typename ScalarTraits< Scalar >::magnitudeType > norms_inf ( const MultiVectorBase< Scalar > & V )

template<class Scalar >

void dots	(	const MultiVectorBase< Scalar > &	V1,
		const MultiVectorBase< Scalar > &	V2,
		const ArrayView< Scalar > &	dots
	)

Parameters

V1	[in]
V2	[in]
dots	[out] Array (size `m = V1->domain()->dim()`) of the dot products `dot[j] = dot(V1.col(j),V2.col(j))`, for `j=0...m-1`, computed using a single reduction.

template<class Scalar >

void sums	(	const MultiVectorBase< Scalar > &	V,
		const ArrayView< Scalar > &	sums
	)

Parameters

V	[in]
sums	[outt] Array (size `m = V->domain()->dim()`) of the sums products `sum[j] = sum(*V.col(j))`, for `j=0...m-1`, computed using a single reduction.

template<class Scalar >

ScalarTraits< Scalar >::magnitudeType norm_1 ( const MultiVectorBase< Scalar > & V )

template<class Scalar >

void scale	(	Scalar	alpha,
		const Ptr< MultiVectorBase< Scalar > > &	V
	)

Note, if alpha==0.0 then V=0.0 is performed, and if alpha==1.0 then nothing is done.

template<class Scalar >

void scaleUpdate	(	const VectorBase< Scalar > &	a,
		const MultiVectorBase< Scalar > &	U,
		const Ptr< MultiVectorBase< Scalar > > &	V
	)

template<class Scalar >

void assign	(	const Ptr< MultiVectorBase< Scalar > > &	V,
		Scalar	alpha
	)

template<class Scalar >

void assign	(	const Ptr< MultiVectorBase< Scalar > > &	V,
		const MultiVectorBase< Scalar > &	U
	)

template<class Scalar >

void update	(	Scalar	alpha,
		const MultiVectorBase< Scalar > &	U,
		const Ptr< MultiVectorBase< Scalar > > &	V
	)

template<class Scalar >

void update	(	const ArrayView< const Scalar > &	alpha,
		Scalar	beta,
		const MultiVectorBase< Scalar > &	U,
		const Ptr< MultiVectorBase< Scalar > > &	V
	)

U.domain()->dim()-1.

template<class Scalar >

void update	(	const MultiVectorBase< Scalar > &	U,
		const ArrayView< const Scalar > &	alpha,
		Scalar	beta,
		const Ptr< MultiVectorBase< Scalar > > &	V
	)

template<class Scalar >

void linear_combination	(	const ArrayView< const Scalar > &	alpha,
		const ArrayView< const Ptr< const MultiVectorBase< Scalar > > > &	X,
		const Scalar &	beta,
		const Ptr< MultiVectorBase< Scalar > > &	Y
	)

Parameters

alpha	[in] Array (length `m`) of input scalars.
X	[in] Array (length `m`) of input multi-vectors.
beta	[in] Scalar multiplier for Y
Y	[in/out] Target multi-vector that is the result of the linear combination.

This function implements a general linear combination:

Y.col(j)(i) = beta*Y.col(j)(i) + alpha[0]*X[0].col(j)(i) + alpha[1]*X[1].col(j)(i) + ... + alpha[m-1]*X[m-1].col(j)(i)

   for:
       i = 0...y->space()->dim()-1
       j = 0...y->domain()->dim()-1

and does so on a single call to MultiVectorBase::applyOp().

template<class Scalar >

void randomize	(	Scalar	l,
		Scalar	u,
		const Ptr< MultiVectorBase< Scalar > > &	V
	)

The elements get_ele(*V->col(j)) are randomly generated between [l,u].

The seed is set using seed_randomize()

template<class Scalar >

void Vt_S	(	const Ptr< MultiVectorBase< Scalar > > &	Z,
		const Scalar &	alpha
	)

template<class Scalar >

void Vp_S	(	const Ptr< MultiVectorBase< Scalar > > &	Z,
		const Scalar &	alpha
	)

template<class Scalar >

void Vp_V	(	const Ptr< MultiVectorBase< Scalar > > &	Z,
		const MultiVectorBase< Scalar > &	X
	)

template<class Scalar >

void V_VpV	(	const Ptr< MultiVectorBase< Scalar > > &	Z,
		const MultiVectorBase< Scalar > &	X,
		const MultiVectorBase< Scalar > &	Y
	)

template<class Scalar >

void V_VmV	(	const Ptr< MultiVectorBase< Scalar > > &	Z,
		const MultiVectorBase< Scalar > &	X,
		const MultiVectorBase< Scalar > &	Y
	)

template<class Scalar >

void V_StVpV	(	const Ptr< MultiVectorBase< Scalar > > &	Z,
		const Scalar &	alpha,
		const MultiVectorBase< Scalar > &	X,
		const MultiVectorBase< Scalar > &	Y
	)

The documentation for this class was generated from the following files:

Protected Member Functions

Related Functions

Minimal mathematical functions

Provide access to the columns as VectorBase objects

Multi-vector sub-views

Collective reduction/transformation operator apply functions

Explicit sub-multi-vector access

Cloning

Overridden functions from LinearOpBase

Protected virtual functions to be overridden by subclasses

Detailed Description

template<class Scalar> class Thyra::MultiVectorBase< Scalar >

Outline

Introduction

Changeable and non-changeable views

Accessing the individual columns as vector views

Accessing collections of columns as multi-vector views

Common behavior of vector and multi-vector views

MultiVectorBase as a linear operator

Multi-vector block updates

Multi-vector block inner products

Support for reduction/transformation operations

Collection of pre-written RTOps and wrapper functions

Explicit multi-vector coefficient access

Explicit multi-vector coefficient access utilities

Notes for subclass developers

Member Function Documentation

Friends And Related Function Documentation

template<class Scalar>
class Thyra::MultiVectorBase< Scalar >