Provides the interface to apply upper and lower bound constraints. More...

#include <ROL_BoundConstraint.hpp>

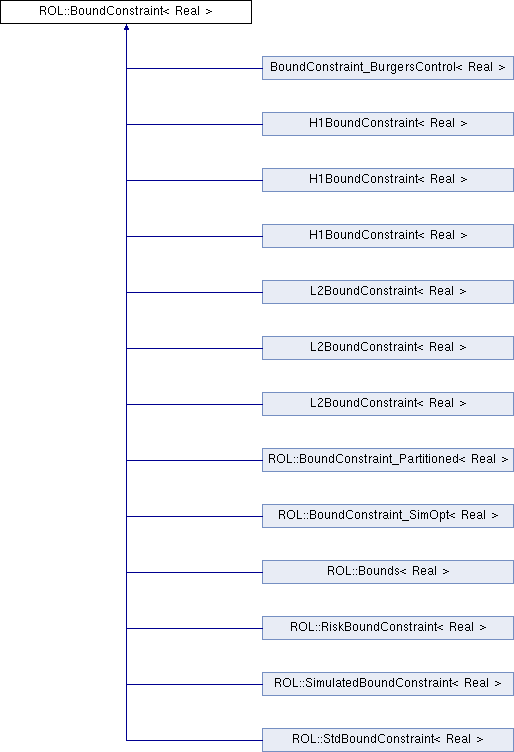
Inheritance diagram for ROL::BoundConstraint< Real >:

Public Member Functions
virtual	~BoundConstraint ()

	BoundConstraint (void)

	BoundConstraint (const Vector< Real > &x)

virtual void	project (Vector< Real > &x)
	Project optimization variables onto the bounds. More...

virtual void	projectInterior (Vector< Real > &x)
	Project optimization variables into the interior of the feasible set. More...

virtual void	pruneUpperActive (Vector< Real > &v, const Vector< Real > &x, Real eps=Real(0))
	Set variables to zero if they correspond to the upper \(\epsilon\)-active set. More...

virtual void	pruneUpperActive (Vector< Real > &v, const Vector< Real > &g, const Vector< Real > &x, Real xeps=Real(0), Real geps=Real(0))
	Set variables to zero if they correspond to the upper \(\epsilon\)-binding set. More...

virtual void	pruneLowerActive (Vector< Real > &v, const Vector< Real > &x, Real eps=Real(0))
	Set variables to zero if they correspond to the lower \(\epsilon\)-active set. More...

virtual void	pruneLowerActive (Vector< Real > &v, const Vector< Real > &g, const Vector< Real > &x, Real xeps=Real(0), Real geps=Real(0))
	Set variables to zero if they correspond to the \(\epsilon\)-binding set. More...

virtual const Ptr< const Vector< Real > >	getLowerBound (void) const
	Return the ref count pointer to the lower bound vector. More...

virtual const Ptr< const Vector< Real > >	getUpperBound (void) const
	Return the ref count pointer to the upper bound vector. More...

virtual bool	isFeasible (const Vector< Real > &v)
	Check if the vector, v, is feasible. More...

virtual void	applyInverseScalingFunction (Vector< Real > &dv, const Vector< Real > &v, const Vector< Real > &x, const Vector< Real > &g) const
	Apply inverse scaling function. More...

virtual void	applyScalingFunctionJacobian (Vector< Real > &dv, const Vector< Real > &v, const Vector< Real > &x, const Vector< Real > &g) const
	Apply scaling function Jacobian. More...

void	activateLower (void)
	Turn on lower bound. More...

void	activateUpper (void)
	Turn on upper bound. More...

void	activate (void)
	Turn on bounds. More...

void	deactivateLower (void)
	Turn off lower bound. More...

void	deactivateUpper (void)
	Turn off upper bound. More...

void	deactivate (void)
	Turn off bounds. More...

bool	isLowerActivated (void) const
	Check if lower bound are on. More...

bool	isUpperActivated (void) const
	Check if upper bound are on. More...

bool	isActivated (void) const
	Check if bounds are on. More...

void	pruneActive (Vector< Real > &v, const Vector< Real > &x, Real eps=Real(0))
	Set variables to zero if they correspond to the \(\epsilon\)-active set. More...

void	pruneActive (Vector< Real > &v, const Vector< Real > &g, const Vector< Real > &x, Real xeps=Real(0), Real geps=Real(0))
	Set variables to zero if they correspond to the \(\epsilon\)-binding set. More...

void	pruneLowerInactive (Vector< Real > &v, const Vector< Real > &x, Real eps=Real(0))
	Set variables to zero if they correspond to the \(\epsilon\)-inactive set. More...

void	pruneUpperInactive (Vector< Real > &v, const Vector< Real > &x, Real eps=Real(0))
	Set variables to zero if they correspond to the \(\epsilon\)-inactive set. More...

void	pruneLowerInactive (Vector< Real > &v, const Vector< Real > &g, const Vector< Real > &x, Real xeps=Real(0), Real geps=Real(0))
	Set variables to zero if they correspond to the \(\epsilon\)-nonbinding set. More...

void	pruneUpperInactive (Vector< Real > &v, const Vector< Real > &g, const Vector< Real > &x, Real xeps=Real(0), Real geps=Real(0))
	Set variables to zero if they correspond to the \(\epsilon\)-nonbinding set. More...

void	pruneInactive (Vector< Real > &v, const Vector< Real > &x, Real eps=Real(0))
	Set variables to zero if they correspond to the \(\epsilon\)-inactive set. More...

void	pruneInactive (Vector< Real > &v, const Vector< Real > &g, const Vector< Real > &x, Real xeps=Real(0), Real geps=Real(0))
	Set variables to zero if they correspond to the \(\epsilon\)-nonbinding set. More...

void	computeProjectedGradient (Vector< Real > &g, const Vector< Real > &x)
	Compute projected gradient. More...

void	computeProjectedStep (Vector< Real > &v, const Vector< Real > &x)
	Compute projected step. More...

Protected Member Functions
Real	computeInf (const Vector< Real > &x) const

Protected Attributes
Ptr< Vector< Real > >	lower_

Ptr< Vector< Real > >	upper_

Private Attributes
bool	Lactivated_
	Flag that determines whether or not the lower bounds are being used. More...

bool	Uactivated_
	Flag that determines whether or not the upper bounds are being used. More...

Detailed Description

template<typename Real>
class ROL::BoundConstraint< Real >

Provides the interface to apply upper and lower bound constraints.

ROL's bound constraint class is to designed to handle point wise bound constraints on optimization variables. That is, let \(\mathcal{X}\) be a Banach space of functions from \(\Xi\) into \(\mathbb{R}\) (for example, \(\Xi\subset\mathbb{R}^d\) for some positive integer \(d\) and \(\mathcal{X}=L^2(\Xi)\) or \(\Xi = \{1,\ldots,n\}\) and \(\mathcal{X}=\mathbb{R}^n\)). For any \(x\in\mathcal{X}\), we consider bounds of the form

\[ a(\xi) \le x(\xi) \le b(\xi) \quad \text{for almost every }\xi\in\Xi. \]

Here, \(a(\xi)\le b(\xi)\) for almost every \(\xi\in\Xi\) and \(a,b\in \mathcal{X}\).

Definition at line 73 of file ROL_BoundConstraint.hpp.

Constructor & Destructor Documentation

template<typename Real>

virtual ROL::BoundConstraint< Real >::~BoundConstraint ( )

inlinevirtual

Definition at line 86 of file ROL_BoundConstraint.hpp.

template<typename Real >

ROL::BoundConstraint< Real >::BoundConstraint ( void )

Definition at line 57 of file ROL_BoundConstraint_Def.hpp.

template<typename Real >

ROL::BoundConstraint< Real >::BoundConstraint ( const Vector< Real > & x )

Definition at line 61 of file ROL_BoundConstraint_Def.hpp.

References ROL::Vector< Real >::clone(), ROL::BoundConstraint< Real >::computeInf(), ROL::BoundConstraint< Real >::lower_, and ROL::BoundConstraint< Real >::upper_.

Member Function Documentation

template<typename Real >

Real ROL::BoundConstraint< Real >::computeInf ( const Vector< Real > & x ) const

protected

Definition at line 50 of file ROL_BoundConstraint_Def.hpp.

References dim, and ROL::Vector< Real >::dimension().

Referenced by ROL::BoundConstraint< Real >::BoundConstraint().

template<typename Real >

void ROL::BoundConstraint< Real >::project ( Vector< Real > & x )

virtual

Project optimization variables onto the bounds.

This function implements the projection of \(x\) onto the bounds, i.e.,

\[ (P_{[a,b]}(x))(\xi) = \min\{b(\xi),\max\{a(\xi),x(\xi)\}\} \quad \text{for almost every }\xi\in\Xi. \]

Parameters

[in,out] x is the optimization variable.

Reimplemented in H1BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, L2BoundConstraint< Real >, BoundConstraint_BurgersControl< Real >, ROL::RiskBoundConstraint< Real >, ROL::Bounds< Real >, ROL::BoundConstraint_Partitioned< Real >, ROL::BoundConstraint_SimOpt< Real >, ROL::SimulatedBoundConstraint< Real >, and ROL::StdBoundConstraint< Real >.

Definition at line 74 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::LineSearchStep< Real >::compute(), ROL::PrimalDualActiveSetStep< Real >::compute(), ROL::PrimalDualActiveSetStep< Real >::computeCriticalityMeasure(), ROL::TrustRegionStep< Real >::computeCriticalityMeasure(), ROL::AugmentedLagrangianStep< Real >::computeGradient(), ROL::FletcherStep< Real >::computeProjGradientNorm(), ROL::LineSearchStep< Real >::GradDotStep(), ROL::Step< Real >::initialize(), ROL::TypeB::KelleySachsAlgorithm< Real >::initialize(), ROL::MoreauYosidaPenaltyStep< Real >::initialize(), ROL::AugmentedLagrangianStep< Real >::initialize(), ROL::PrimalDualActiveSetStep< Real >::initialize(), ROL::TrustRegionStep< Real >::initialize(), ROL::TypeB::KelleySachsAlgorithm< Real >::run(), ROL::TypeB::PrimalDualActiveSetAlgorithm< Real >::run(), ROL::ProjectedNewtonStep< Real >::update(), ROL::ProjectedSecantStep< Real >::update(), ROL::TrustRegion< Real >::update(), ROL::ProjectedNewtonKrylovStep< Real >::update(), ROL::InteriorPointStep< Real >::update(), and ROL::LineSearch< Real >::updateIterate().

template<typename Real >

void ROL::BoundConstraint< Real >::projectInterior ( Vector< Real > & x )

virtual

Project optimization variables into the interior of the feasible set.

This function implements the projection of \(x\) into the interior of the feasible set, i.e.,

\[ (\bar{P}_{[a,b]}(x))(\xi) \in (a(\xi),b(\xi)) \quad \text{for almost every }\xi\in\Xi. \]

Parameters

[in,out] x is the optimization variable.

Reimplemented in ROL::RiskBoundConstraint< Real >, ROL::BoundConstraint_Partitioned< Real >, ROL::BoundConstraint_SimOpt< Real >, ROL::Bounds< Real >, ROL::SimulatedBoundConstraint< Real >, and ROL::StdBoundConstraint< Real >.

Definition at line 81 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::TypeB::InteriorPointAlgorithm< Real >::initialize(), ROL::TypeG::InteriorPointAlgorithm< Real >::initialize(), ROL::InteriorPointStep< Real >::initialize(), and ROL::TrustRegionStep< Real >::initialize().

template<typename Real >

void ROL::BoundConstraint< Real >::pruneUpperActive	(	Vector< Real > &	v,
		const Vector< Real > &	x,
		Real	eps = `Real(0)`
	)

virtual

Set variables to zero if they correspond to the upper \(\epsilon\)-active set.

This function sets \(v(\xi)=0\) if \(\xi\in\mathcal{A}^+_\epsilon(x)\). Here, the upper \(\epsilon\)-active set is defined as

\[ \mathcal{A}^+_\epsilon(x) = \{\,\xi\in\Xi\,:\,x(\xi) \ge b(\xi)-\epsilon\,\}. \]

Parameters

[out]	v	is the variable to be pruned.
[in]	x	is the current optimization variable.
[in]	eps	is the active-set tolerance \(\epsilon\).

Reimplemented in H1BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, L2BoundConstraint< Real >, BoundConstraint_BurgersControl< Real >, ROL::RiskBoundConstraint< Real >, ROL::BoundConstraint_SimOpt< Real >, ROL::BoundConstraint_Partitioned< Real >, ROL::Bounds< Real >, ROL::SimulatedBoundConstraint< Real >, and ROL::StdBoundConstraint< Real >.

Definition at line 88 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::PrimalDualActiveSetStep< Real >::compute().

template<typename Real >

void ROL::BoundConstraint< Real >::pruneUpperActive	(	Vector< Real > &	v,
		const Vector< Real > &	g,
		const Vector< Real > &	x,
		Real	xeps = `Real(0)`,
		Real	geps = `Real(0)`
	)

virtual

Set variables to zero if they correspond to the upper \(\epsilon\)-binding set.

This function sets \(v(\xi)=0\) if \(\xi\in\mathcal{B}^+_\epsilon(x)\). Here, the upper \(\epsilon\)-binding set is defined as

\[ \mathcal{B}^+_\epsilon(x) = \{\,\xi\in\Xi\,:\,x(\xi) \ge b(\xi)-\epsilon_x,\; g(\xi) < -\epsilon_g \,\}. \]

Parameters

[out]	v	is the variable to be pruned.
[in]	g	is the negative search direction.
[in]	x	is the current optimization variable.
[in]	xeps	is the active-set tolerance \(\epsilon_x\).
[in]	geps	is the binding-set tolerance \(\epsilon_g\).

Reimplemented in H1BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, L2BoundConstraint< Real >, BoundConstraint_BurgersControl< Real >, ROL::RiskBoundConstraint< Real >, ROL::BoundConstraint_SimOpt< Real >, ROL::BoundConstraint_Partitioned< Real >, ROL::Bounds< Real >, ROL::SimulatedBoundConstraint< Real >, and ROL::StdBoundConstraint< Real >.

Definition at line 95 of file ROL_BoundConstraint_Def.hpp.

template<typename Real >

void ROL::BoundConstraint< Real >::pruneLowerActive	(	Vector< Real > &	v,
		const Vector< Real > &	x,
		Real	eps = `Real(0)`
	)

virtual

Set variables to zero if they correspond to the lower \(\epsilon\)-active set.

This function sets \(v(\xi)=0\) if \(\xi\in\mathcal{A}^-_\epsilon(x)\). Here, the lower \(\epsilon\)-active set is defined as

\[ \mathcal{A}^-_\epsilon(x) = \{\,\xi\in\Xi\,:\,x(\xi) \le a(\xi)+\epsilon\,\}. \]

Parameters

[out]	v	is the variable to be pruned.
[in]	x	is the current optimization variable.
[in]	eps	is the active-set tolerance \(\epsilon\).

Reimplemented in H1BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, L2BoundConstraint< Real >, BoundConstraint_BurgersControl< Real >, ROL::RiskBoundConstraint< Real >, ROL::BoundConstraint_SimOpt< Real >, ROL::BoundConstraint_Partitioned< Real >, ROL::Bounds< Real >, ROL::SimulatedBoundConstraint< Real >, and ROL::StdBoundConstraint< Real >.

Definition at line 102 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::PrimalDualActiveSetStep< Real >::compute().

template<typename Real >

void ROL::BoundConstraint< Real >::pruneLowerActive	(	Vector< Real > &	v,
		const Vector< Real > &	g,
		const Vector< Real > &	x,
		Real	xeps = `Real(0)`,
		Real	geps = `Real(0)`
	)

virtual

Set variables to zero if they correspond to the \(\epsilon\)-binding set.

This function sets \(v(\xi)=0\) if \(\xi\in\mathcal{B}^-_\epsilon(x)\). Here, the lower \(\epsilon\)-binding set is defined as

\[ \mathcal{B}^-_\epsilon(x) = \{\,\xi\in\Xi\,:\,x(\xi) \le a(\xi)+\epsilon,\; g(\xi) > 0 \,\}. \]

Parameters

[out]	v	is the variable to be pruned.
[in]	g	is the negative search direction.
[in]	x	is the current optimization variable.
[in]	xeps	is the active-set tolerance \(\epsilon_x\).
[in]	geps	is the binding-set tolerance \(\epsilon_g\).

Reimplemented in H1BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, L2BoundConstraint< Real >, BoundConstraint_BurgersControl< Real >, ROL::RiskBoundConstraint< Real >, ROL::BoundConstraint_SimOpt< Real >, ROL::BoundConstraint_Partitioned< Real >, ROL::Bounds< Real >, ROL::SimulatedBoundConstraint< Real >, and ROL::StdBoundConstraint< Real >.

Definition at line 109 of file ROL_BoundConstraint_Def.hpp.

template<typename Real >

const Ptr< const Vector< Real > > ROL::BoundConstraint< Real >::getLowerBound ( void ) const

virtual

Return the ref count pointer to the lower bound vector.

Reimplemented in H1BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, L2BoundConstraint< Real >, ROL::RiskBoundConstraint< Real >, ROL::BoundConstraint_SimOpt< Real >, and ROL::SimulatedBoundConstraint< Real >.

Definition at line 116 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::BoundConstraint_Partitioned< Real >::BoundConstraint_Partitioned(), ROL::PrimalDualActiveSetStep< Real >::compute(), ROL::LowerBoundToConstraint< Real >::LowerBoundToConstraint(), ROL::RandomizeFeasibleVector(), and ROL::TypeB::PrimalDualActiveSetAlgorithm< Real >::run().

template<typename Real >

const Ptr< const Vector< Real > > ROL::BoundConstraint< Real >::getUpperBound ( void ) const

virtual

Return the ref count pointer to the upper bound vector.

Reimplemented in H1BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, L2BoundConstraint< Real >, ROL::RiskBoundConstraint< Real >, ROL::BoundConstraint_SimOpt< Real >, and ROL::SimulatedBoundConstraint< Real >.

Definition at line 124 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::BoundConstraint_Partitioned< Real >::BoundConstraint_Partitioned(), ROL::PrimalDualActiveSetStep< Real >::compute(), ROL::RandomizeFeasibleVector(), ROL::TypeB::PrimalDualActiveSetAlgorithm< Real >::run(), and ROL::UpperBoundToConstraint< Real >::UpperBoundToConstraint().

template<typename Real >

bool ROL::BoundConstraint< Real >::isFeasible ( const Vector< Real > & v )

virtual

Check if the vector, v, is feasible.

This function returns true if \(v = P_{[a,b]}(v)\).

Parameters

[in] v is the vector to be checked.

Reimplemented in H1BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, H1BoundConstraint< Real >, L2BoundConstraint< Real >, L2BoundConstraint< Real >, BoundConstraint_BurgersControl< Real >, ROL::RiskBoundConstraint< Real >, ROL::BoundConstraint_SimOpt< Real >, ROL::BoundConstraint_Partitioned< Real >, ROL::Bounds< Real >, ROL::SimulatedBoundConstraint< Real >, and ROL::StdBoundConstraint< Real >.

Definition at line 132 of file ROL_BoundConstraint_Def.hpp.

References ROL::Vector< Real >::clone().

Referenced by ROL::TypeB::LSecantBAlgorithm< Real >::dpcg(), ROL::TypeB::PrimalDualActiveSetAlgorithm< Real >::run(), ROL::TrustRegion< Real >::update(), and ROL::PrimalDualActiveSetStep< Real >::update().

template<typename Real >

void ROL::BoundConstraint< Real >::applyInverseScalingFunction	(	Vector< Real > &	dv,
		const Vector< Real > &	v,
		const Vector< Real > &	x,
		const Vector< Real > &	g
	)		const

virtual

Apply inverse scaling function.

This function applies the inverse scaling function \(d(x,g)\) to a vector \(v\), i.e., the output is \(\mathrm{diag}(d(x,g)^{-1})v\). The scaling function must satisfy: (i) \(d(x,g)_i = 0\) if \(x_i = a_i\) and \(g_i \ge 0\); (ii) \(d(x,g)_i = 0\) if \(x_i = b_i\) and \(g_i \le 0\); and (iii) \(d(x,g)_i > 0\) otherwise.

Parameters

[out]	dv	is the inverse scaling function applied to v.
[in]	v	is the vector being scaled.
[in]	x	is the primal vector at which the scaling function is evaluated.
[in]	g	is the dual vector at which the scaling function is evaluated.

Reimplemented in ROL::RiskBoundConstraint< Real >, ROL::BoundConstraint_SimOpt< Real >, ROL::BoundConstraint_Partitioned< Real >, ROL::SimulatedBoundConstraint< Real >, ROL::Bounds< Real >, and ROL::StdBoundConstraint< Real >.

Definition at line 146 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::TypeB::ColemanLiAlgorithm< Real >::applyC().

template<typename Real >

void ROL::BoundConstraint< Real >::applyScalingFunctionJacobian	(	Vector< Real > &	dv,
		const Vector< Real > &	v,
		const Vector< Real > &	x,
		const Vector< Real > &	g
	)		const

virtual

Apply scaling function Jacobian.

This function applies the Jacobian of the scaling function \(d(x,g)\) to a vector \(v\). The output is \(\mathrm{diag}(d_x(x,g)g)v\). The scaling function must satisfy: (i) \(d(x,g)_i = 0\) if \(x_i = a_i\) and \(g_i \ge 0\); (ii) \(d(x,g)_i = 0\) if \(x_i = b_i\) and \(g_i \le 0\); and (iii) \(d(x,g)_i > 0\) otherwise.

Parameters

[out]	dv	is the scaling function Jacobian applied to v.
[in]	v	is the vector being scaled.
[in]	x	is the primal vector at which the scaling function is evaluated.
[in]	g	is the dual vector at which the scaling function is evaluated.

Reimplemented in ROL::RiskBoundConstraint< Real >, ROL::BoundConstraint_SimOpt< Real >, ROL::BoundConstraint_Partitioned< Real >, ROL::SimulatedBoundConstraint< Real >, ROL::Bounds< Real >, and ROL::StdBoundConstraint< Real >.

Definition at line 151 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::TypeB::ColemanLiAlgorithm< Real >::applyC().

template<typename Real >

void ROL::BoundConstraint< Real >::activateLower ( void )

Turn on lower bound.

This function turns on lower bounds.

Definition at line 156 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::Bounds< Real >::Bounds(), and ROL::StdBoundConstraint< Real >::StdBoundConstraint().

template<typename Real >

void ROL::BoundConstraint< Real >::activateUpper ( void )

Turn on upper bound.

This function turns on upper bounds.

Definition at line 161 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::Bounds< Real >::Bounds(), and ROL::StdBoundConstraint< Real >::StdBoundConstraint().

template<typename Real >

void ROL::BoundConstraint< Real >::activate ( void )

Turn on bounds.

This function turns the bounds on.

Definition at line 166 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::BoundConstraint_Partitioned< Real >::BoundConstraint_Partitioned(), ROL::RiskBoundConstraint< Real >::RiskBoundConstraint(), and ROL::StdBoundConstraint< Real >::StdBoundConstraint().

template<typename Real >

void ROL::BoundConstraint< Real >::deactivateLower ( void )

Turn off lower bound.

This function turns the lower bounds off.

Definition at line 172 of file ROL_BoundConstraint_Def.hpp.

template<typename Real >

void ROL::BoundConstraint< Real >::deactivateUpper ( void )

Turn off upper bound.

This function turns the upper bounds off.

Definition at line 177 of file ROL_BoundConstraint_Def.hpp.

template<typename Real >

void ROL::BoundConstraint< Real >::deactivate ( void )

Turn off bounds.

This function turns the bounds off.

Definition at line 182 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::BoundConstraint_Partitioned< Real >::BoundConstraint_Partitioned(), ROL::BoundConstraint_SimOpt< Real >::BoundConstraint_SimOpt(), ROL::RiskBoundConstraint< Real >::RiskBoundConstraint(), and ROL::Algorithm< Real >::run().

template<typename Real >

bool ROL::BoundConstraint< Real >::isLowerActivated ( void ) const

Check if lower bound are on.

This function returns true if the lower bounds are turned on.

Definition at line 188 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::BoundConstraint_Partitioned< Real >::BoundConstraint_Partitioned(), and ROL::ObjectiveFromBoundConstraint< Real >::ObjectiveFromBoundConstraint().

template<typename Real >

bool ROL::BoundConstraint< Real >::isUpperActivated ( void ) const

Check if upper bound are on.

This function returns true if the upper bounds are turned on.

Definition at line 193 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::BoundConstraint_Partitioned< Real >::BoundConstraint_Partitioned(), and ROL::ObjectiveFromBoundConstraint< Real >::ObjectiveFromBoundConstraint().

template<typename Real >

bool ROL::BoundConstraint< Real >::isActivated ( void ) const

Check if bounds are on.

This function returns true if the bounds are turned on.

Definition at line 198 of file ROL_BoundConstraint_Def.hpp.

template<typename Real >

void ROL::BoundConstraint< Real >::pruneActive	(	Vector< Real > &	v,
		const Vector< Real > &	x,
		Real	eps = `Real(0)`
	)

Set variables to zero if they correspond to the \(\epsilon\)-active set.

This function sets \(v(\xi)=0\) if \(\xi\in\mathcal{A}_\epsilon(x)\). Here, the \(\epsilon\)-active set is defined as

\[ \mathcal{A}_\epsilon(x) = \mathcal{A}^+_\epsilon(x)\cap\mathcal{A}^-_\epsilon(x). \]

Parameters

[out]	v	is the variable to be pruned.
[in]	x	is the current optimization variable.
[in]	eps	is the active-set tolerance \(\epsilon\).

Definition at line 203 of file ROL_BoundConstraint_Def.hpp.

Referenced by ROL::TypeB::KelleySachsAlgorithm< Real >::applyFreeHessian(), ROL::TypeB::LSecantBAlgorithm< Real >::applyFreeHessian(), ROL::TypeB::LinMoreAlgorithm< Real >::applyFreeHessian(), ROL::TypeB::KelleySachsAlgorithm< Real >::applyFreePrecond(), ROL::TypeB::LSecantBAlgorithm< Real >::applyFreePrecond(), ROL::TypeB::LinMoreAlgorithm< Real >::applyFreePrecond(), ROL::ProjectedNewtonStep< Real >::compute(), ROL::ProjectedSecantStep< Real >::compute(), ROL::PrimalDualActiveSetStep< Real >::compute(), ROL::LineSearchStep< Real >::GradDotStep(), ROL::TypeB::LSecantBAlgorithm< Real >::run(), ROL::TypeB::KelleySachsAlgorithm< Real >::run(), ROL::TypeB::LinMoreAlgorithm< Real >::run(), ROL::TypeB::PrimalDualActiveSetAlgorithm< Real >::run(), ROL::LineSearch< Real >::status(), and ROL::TrustRegion< Real >::update().

template<typename Real >

void ROL::BoundConstraint< Real >::pruneActive	(	Vector< Real > &	v,
		const Vector< Real > &	g,
		const Vector< Real > &	x,
		Real	xeps = `Real(0)`,
		Real	geps = `Real(0)`
	)

Set variables to zero if they correspond to the \(\epsilon\)-binding set.

This function sets \(v(\xi)=0\) if \(\xi\in\mathcal{B}_\epsilon(x)\). Here, the \(\epsilon\)-binding set is defined as

\[ \mathcal{B}^+_\epsilon(x) = \mathcal{B}^+_\epsilon(x)\cap\mathcal{B}^-_\epsilon(x). \]

Parameters

[out]	v	is the variable to be pruned.
[in]	g	is the negative search direction.
[in]	x	is the current optimization variable.
[in]	xeps	is the active-set tolerance \(\epsilon_x\).
[in]	geps	is the binding-set tolerance \(\epsilon_g\).

Definition at line 211 of file ROL_BoundConstraint_Def.hpp.

template<typename Real >

void ROL::BoundConstraint< Real >::pruneLowerInactive	(	Vector< Real > &	v,
		const Vector< Real > &	x,
		Real	eps = `Real(0)`
	)

Set variables to zero if they correspond to the \(\epsilon\)-inactive set.

This function sets \(v(\xi)=0\) if \(\xi\in\Xi\setminus\mathcal{A}_\epsilon(x)\). Here,

Parameters

[out]	v	is the variable to be pruned.
[in]	x	is the current optimization variable.
[in]	eps	is the active-set tolerance \(\epsilon\).

Definition at line 219 of file ROL_BoundConstraint_Def.hpp.

References ROL::Vector< Real >::axpy(), and ROL::Vector< Real >::clone().

Referenced by ROL::TypeB::PrimalDualActiveSetAlgorithm< Real >::run().

template<typename Real >

void ROL::BoundConstraint< Real >::pruneUpperInactive	(	Vector< Real > &	v,
		const Vector< Real > &	x,
		Real	eps = `Real(0)`
	)

Set variables to zero if they correspond to the \(\epsilon\)-inactive set.

This function sets \(v(\xi)=0\) if \(\xi\in\Xi\setminus\mathcal{A}_\epsilon(x)\). Here,

Parameters

[out]	v	is the variable to be pruned.
[in]	x	is the current optimization variable.
[in]	eps	is the active-set tolerance \(\epsilon\).

Definition at line 230 of file ROL_BoundConstraint_Def.hpp.

References ROL::Vector< Real >::axpy(), and ROL::Vector< Real >::clone().

Referenced by ROL::TypeB::PrimalDualActiveSetAlgorithm< Real >::run().

template<typename Real >

void ROL::BoundConstraint< Real >::pruneLowerInactive	(	Vector< Real > &	v,
		const Vector< Real > &	g,
		const Vector< Real > &	x,
		Real	xeps = `Real(0)`,
		Real	geps = `Real(0)`
	)

Set variables to zero if they correspond to the \(\epsilon\)-nonbinding set.

This function sets \(v(\xi)=0\) if \(\xi\in\Xi\setminus\mathcal{B}_\epsilon(x)\).

Parameters

[out]	v	is the variable to be pruned.
[in]	x	is the current optimization variable.
[in]	g	is the negative search direction.
[in]	xeps	is the active-set tolerance \(\epsilon_x\).
[in]	geps	is the binding-set tolerance \(\epsilon_g\).

Definition at line 241 of file ROL_BoundConstraint_Def.hpp.

References ROL::Vector< Real >::axpy(), and ROL::Vector< Real >::clone().

template<typename Real >

void ROL::BoundConstraint< Real >::pruneUpperInactive	(	Vector< Real > &	v,
		const Vector< Real > &	g,
		const Vector< Real > &	x,
		Real	xeps = `Real(0)`,
		Real	geps = `Real(0)`
	)

Set variables to zero if they correspond to the \(\epsilon\)-nonbinding set.

This function sets \(v(\xi)=0\) if \(\xi\in\Xi\setminus\mathcal{B}_\epsilon(x)\).

Parameters

[out]	v	is the variable to be pruned.
[in]	x	is the current optimization variable.
[in]	g	is the negative search direction.
[in]	xeps	is the active-set tolerance \(\epsilon_x\).
[in]	geps	is the binding-set tolerance \(\epsilon_g\).

Definition at line 252 of file ROL_BoundConstraint_Def.hpp.

References ROL::Vector< Real >::axpy(), and ROL::Vector< Real >::clone().

template<typename Real >

void ROL::BoundConstraint< Real >::pruneInactive	(	Vector< Real > &	v,
		const Vector< Real > &	x,
		Real	eps = `Real(0)`
	)

Set variables to zero if they correspond to the \(\epsilon\)-inactive set.

This function sets \(v(\xi)=0\) if \(\xi\in\Xi\setminus\mathcal{A}_\epsilon(x)\). Here,

Parameters

[out]	v	is the variable to be pruned.
[in]	x	is the current optimization variable.
[in]	eps	is the active-set tolerance \(\epsilon\).

Definition at line 263 of file ROL_BoundConstraint_Def.hpp.

References ROL::Vector< Real >::axpy(), and ROL::Vector< Real >::clone().

Referenced by ROL::TypeB::KelleySachsAlgorithm< Real >::applyFreeHessian(), ROL::TypeB::KelleySachsAlgorithm< Real >::applyFreePrecond(), ROL::ProjectedNewtonStep< Real >::compute(), ROL::ProjectedSecantStep< Real >::compute(), ROL::LineSearchStep< Real >::GradDotStep(), ROL::TypeB::PrimalDualActiveSetAlgorithm< Real >::run(), and ROL::LineSearch< Real >::status().

template<typename Real >

void ROL::BoundConstraint< Real >::pruneInactive	(	Vector< Real > &	v,
		const Vector< Real > &	g,
		const Vector< Real > &	x,
		Real	xeps = `Real(0)`,
		Real	geps = `Real(0)`
	)

Set variables to zero if they correspond to the \(\epsilon\)-nonbinding set.

This function sets \(v(\xi)=0\) if \(\xi\in\Xi\setminus\mathcal{B}_\epsilon(x)\).

Parameters

[out]	v	is the variable to be pruned.
[in]	x	is the current optimization variable.
[in]	g	is the negative search direction.
[in]	xeps	is the active-set tolerance \(\epsilon_x\).
[in]	geps	is the binding-set tolerance \(\epsilon_g\).