|
Tpetra parallel linear algebra
Version of the Day
|
|
Tpetra parallel linear algebra
Version of the Day
|
Namespace Tpetra contains the class and methods constituting the Tpetra library. More...
Namespaces | |
| Details | |
| Nonmember function that computes a residual Computes R = B - A * X. | |
| Impl | |
| Namespace for new Tpetra features that are not ready for public release, but are ready for evaluation by friendly expert users. | |
| Ext | |
| Namespace for external Tpetra functionality. | |
| MatrixMatrix | |
| Distributed sparse matrix-matrix multiply and add. | |
| TripleMatrixMultiply | |
| Distributed sparse triple matrix product. | |
Classes | |
| class | BlockCrsMatrix |
| Sparse matrix whose entries are small dense square blocks, all of the same dimensions. More... | |
| class | BlockMultiVector |
| MultiVector for multiple degrees of freedom per mesh point. More... | |
| class | BlockVector |
| Vector for multiple degrees of freedom per mesh point. More... | |
| class | project1st |
| Binary function that returns its first argument. More... | |
| class | project2nd |
| Binary function that returns its second argument. More... | |
| class | ScopeGuard |
| Scope guard whose destructor automatically calls Tpetra::finalize for you. More... | |
| struct | RowInfo |
| Allocation information for a locally owned row in a CrsGraph or CrsMatrix. More... | |
| class | CrsGraph |
| A distributed graph accessed by rows (adjacency lists) and stored sparsely. More... | |
| class | CrsGraphTransposer |
| Construct and (optionally) redistribute the explicitly stored transpose of a CrsGraph. More... | |
| class | CrsMatrix |
| Sparse matrix that presents a row-oriented interface that lets users read or modify entries. More... | |
| class | CrsMatrixMultiplyOp |
| A class for wrapping a CrsMatrix multiply in a Operator. More... | |
| class | MultiVector |
| One or more distributed dense vectors. More... | |
| class | Directory |
| Implement mapping from global ID to process ID and local ID. More... | |
| class | DistObject |
| Base class for distributed Tpetra objects that support data redistribution. More... | |
| class | Distributor |
| Sets up and executes a communication plan for a Tpetra DistObject. More... | |
| class | Export |
| Communication plan for data redistribution from a (possibly) multiply-owned to a uniquely-owned distribution. More... | |
| class | FECrsGraph |
| A distributed graph accessed by rows (adjacency lists) and stored sparsely. More... | |
| class | FECrsMatrix |
| Sparse matrix that presents a row-oriented interface that lets users read or modify entries. More... | |
| class | Import |
| Communication plan for data redistribution from a uniquely-owned to a (possibly) multiply-owned distribution. More... | |
| class | ImportExportData |
| Implementation detail of Import and Export. More... | |
| class | LinearProblem |
| Class that encapulates linear problem (Ax = b). More... | |
| class | LocalCrsMatrixOperator |
| Abstract interface for local operators (e.g., matrices and preconditioners). More... | |
| class | LocalOperator |
| Abstract interface for local operators (e.g., matrices and preconditioners). More... | |
| class | Map |
| A parallel distribution of indices over processes. More... | |
| class | MixedScalarMultiplyOp |
| A class for wrapping an Operator of one Scalar type into an Operator of another Scalar type. More... | |
| class | Operator |
| Abstract interface for operators (e.g., matrices and preconditioners). More... | |
| class | Packable |
| Abstract base class for objects that can be the source of an Import or Export operation, and that also know how to pack their data to send to the target object. More... | |
| class | RowGraph |
| An abstract interface for graphs accessed by rows. More... | |
| class | RowMatrix |
| A read-only, row-oriented interface to a sparse matrix. More... | |
| class | RowMatrixTransposer |
| Construct and (optionally) redistribute the explicitly stored transpose of a CrsMatrix. More... | |
| class | BlockCrsMatrixTransposer |
| Construct and (optionally) redistribute the explicitly stored transpose of a BlockCrsMatrix. More... | |
| class | SolverMap_CrsMatrix |
| class | SolverMap_LinearProblem |
| class | SrcDistObject |
| Abstract base class for objects that can be the source of an Import or Export operation. More... | |
| class | Transform |
| class | Vector |
| A distributed dense vector. More... | |
| class | CrsMatrixStruct |
| Struct that holds views of the contents of a CrsMatrix. More... | |
| class | BlockCrsMatrixStruct |
| Struct that holds views of the contents of a BlockCrsMatrix. More... | |
Typedefs | |
| typedef Teuchos_Ordinal | Array_size_type |
| Size type for Teuchos Array objects. More... | |
| typedef size_t | global_size_t |
| Global size_t object. More... | |
Enumerations | |
| enum | CombineMode { ADD, INSERT, REPLACE, ABSMAX, ZERO, ADD_ASSIGN } |
| Rule for combining data in an Import or Export. More... | |
| enum | LocalGlobal |
| Enum for local versus global allocation of Map entries. More... | |
| enum | LookupStatus { AllIDsPresent, IDNotPresent } |
| Return status of Map remote index lookup (getRemoteIndexList()). More... | |
| enum | OptimizeOption { DoOptimizeStorage, DoNotOptimizeStorage } |
| enum | ESweepDirection |
| Sweep direction for Gauss-Seidel or Successive Over-Relaxation (SOR). More... | |
| enum | EScaling |
| Whether "scaling" a matrix means multiplying or dividing its entries. More... | |
Functions | |
| template<class CrsMatrixType > | |
| void | applyDirichletBoundaryConditionToLocalMatrixRows (const typename CrsMatrixType::execution_space &execSpace, CrsMatrixType &A, const Kokkos::View< typename CrsMatrixType::local_ordinal_type *, typename CrsMatrixType::device_type > &lclRowInds) |
For all k in [0, lclRowInds.extent(0)), set local row lclRowInds[k] of A to have 1 on the diagonal and 0 elsewhere. Run on device. More... | |
| template<class CrsMatrixType > | |
| void | applyDirichletBoundaryConditionToLocalMatrixRows (CrsMatrixType &A, const Kokkos::View< typename CrsMatrixType::local_ordinal_type *, typename CrsMatrixType::device_type > &lclRowInds) |
For all k in [0, lclRowInds.extent(0)), set local row lclRowInds[k] of A to have 1 on the diagonal and 0 elsewhere. Run on device, using the default execution space instance. More... | |
| template<class CrsMatrixType > | |
| void | applyDirichletBoundaryConditionToLocalMatrixRows (CrsMatrixType &A, const Kokkos::View< typename CrsMatrixType::local_ordinal_type *, Kokkos::HostSpace > &lclRowInds) |
For all k in [0, lclRowInds.extent(0)), set local row lclRowInds[k] of A to have 1 on the diagonal and 0 elsewhere. Run on host, using the default host execution space instance. More... | |
| template<class CrsMatrixType > | |
| void | applyDirichletBoundaryConditionToLocalMatrixRowsAndColumns (const typename CrsMatrixType::execution_space &execSpace, CrsMatrixType &A, const Kokkos::View< typename CrsMatrixType::local_ordinal_type *, typename CrsMatrixType::device_type > &lclRowInds) |
For all k in [0, lclRowInds.extent(0)), set local row and column lclRowInds[k] of A to have 1 on the diagonal and 0 elsewhere. Run on host, using the default host execution space instance. More... | |
| template<class CrsMatrixType > | |
| void | applyDirichletBoundaryConditionToLocalMatrixRowsAndColumns (CrsMatrixType &A, const Kokkos::View< typename CrsMatrixType::local_ordinal_type *, Kokkos::HostSpace > &lclRowInds) |
For all k in [0, lclRowInds.extent(0)), set local row and column lclRowInds[k] of A to have 1 on the diagonal and 0 elsewhere. Run on host, using the default host execution space instance. More... | |
| template<class CrsMatrixType > | |
| void | applyDirichletBoundaryConditionToLocalMatrixRowsAndColumns (CrsMatrixType &A, const Kokkos::View< typename CrsMatrixType::local_ordinal_type *, typename CrsMatrixType::device_type > &lclRowInds) |
For all k in [0, lclRowInds.extent(0)), set local row and column lclRowInds[k] of A to have 1 on the diagonal and 0 elsewhere. Run on host, using the default host execution space instance. More... | |
| template<class Scalar , class LO , class GO , class Node > | |
| void | blockCrsMatrixWriter (BlockCrsMatrix< Scalar, LO, GO, Node > const &A, std::string const &fileName) |
| Helper function to write a BlockCrsMatrix. Calls the 3-argument version. More... | |
| template<class Scalar , class LO , class GO , class Node > | |
| void | blockCrsMatrixWriter (BlockCrsMatrix< Scalar, LO, GO, Node > const &A, std::string const &fileName, Teuchos::ParameterList const ¶ms) |
| Helper function to write a BlockCrsMatrix. Calls the 3-argument version. More... | |
| template<class Scalar , class LO , class GO , class Node > | |
| void | blockCrsMatrixWriter (BlockCrsMatrix< Scalar, LO, GO, Node > const &A, std::ostream &os) |
| Helper function to write a BlockCrsMatrix. Calls the 3-argument version. More... | |
| template<class Scalar , class LO , class GO , class Node > | |
| void | blockCrsMatrixWriter (BlockCrsMatrix< Scalar, LO, GO, Node > const &A, std::ostream &os, Teuchos::ParameterList const ¶ms) |
| Helper function to write a BlockCrsMatrix. More... | |
| template<class Scalar , class LO , class GO , class Node > | |
| void | writeMatrixStrip (BlockCrsMatrix< Scalar, LO, GO, Node > const &A, std::ostream &os, Teuchos::ParameterList const ¶ms) |
| Helper function called by blockCrsMatrixWriter. More... | |
| template<class Scalar , class LO , class GO , class Node > | |
| Teuchos::RCP< Tpetra::CrsGraph < LO, GO, Node > > | getBlockCrsGraph (const Tpetra::CrsMatrix< Scalar, LO, GO, Node > &pointMatrix, const LO &blockSize, bool use_local_ID=true) |
| Non-member constructor that creates the CrsGraph of a BlockCrsMatrix from an existing point CrsMatrix and a block size. More... | |
| template<class Scalar , class LO , class GO , class Node > | |
| Teuchos::RCP< BlockCrsMatrix < Scalar, LO, GO, Node > > | convertToBlockCrsMatrix (const Tpetra::CrsMatrix< Scalar, LO, GO, Node > &pointMatrix, const LO &blockSize, bool use_local_ID=true) |
| Non-member constructor that creates a BlockCrsMatrix from an existing point CrsMatrix. More... | |
| template<class Scalar , class LO , class GO , class Node > | |
| Teuchos::RCP < Tpetra::CrsMatrix< Scalar, LO, GO, Node > > | fillLogicalBlocks (const Tpetra::CrsMatrix< Scalar, LO, GO, Node > &pointMatrix, const LO &blockSize) |
| Fill all point entries in a logical block of a CrsMatrix with zeroes. This should be called before convertToBlockCrsMatrix if your Crs is not filled. Performed on host. More... | |
| template<class Scalar , class LO , class GO , class Node > | |
| Teuchos::RCP < Tpetra::CrsMatrix< Scalar, LO, GO, Node > > | unfillFormerBlockCrs (const Tpetra::CrsMatrix< Scalar, LO, GO, Node > &pointMatrix) |
| Unfill all point entries in a logical block of a CrsMatrix with zeroes. This can be called after convertToCrsMatrix if you don't want to keep the filled values. Performed on host. More... | |
| template<class LO , class GO , class Node > | |
| Teuchos::RCP< const Tpetra::Map< LO, GO, Node > > | createMeshMap (LO const &blockSize, const Tpetra::Map< LO, GO, Node > &pointMap, bool use_local_ID=false) |
| Helper function to generate a mesh map from a point map. Important! It's assumed that point GIDs associated with a single mesh GID appear consecutively in pointMap. More... | |
| template<class Scalar , class LO , class GO , class Node > | |
| Teuchos::RCP< CrsMatrix < Scalar, LO, GO, Node > > | convertToCrsMatrix (const Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node > &blockMatrix) |
| Non-member constructor that creates a point CrsMatrix from an existing BlockCrsMatrix. More... | |
| template<class LO , class GO , class Node > | |
| Teuchos::RCP< const Tpetra::Map< LO, GO, Node > > | createPointMap (LO const &blockSize, const Tpetra::Map< LO, GO, Node > &blockMap) |
| Helper function to generate a point map from a block map (with a given block size) GIDs associated with a single mesh GID appear consecutively in the output map. More... | |
| template<class ViewType , class CoefficientType , class IndexType = int, const int rank = ViewType::rank> | |
| KOKKOS_INLINE_FUNCTION void | SCAL (const CoefficientType &alpha, const ViewType &x) |
| x := alpha*x, where x is either rank 1 (a vector) or rank 2 (a matrix). More... | |
| template<class ViewType , class InputType , class IndexType = int, const int rank = ViewType::rank> | |
| KOKKOS_INLINE_FUNCTION void | FILL (const ViewType &x, const InputType &val) |
| Set every entry of x to val. More... | |
| template<class CoefficientType , class ViewType1 , class ViewType2 , class IndexType = int, const int rank = ViewType1::rank> | |
| KOKKOS_INLINE_FUNCTION void | AXPY (const CoefficientType &alpha, const ViewType1 &x, const ViewType2 &y) |
y := y + alpha * x (dense vector or matrix update) More... | |
| template<class ViewType1 , class ViewType2 , class IndexType = int, const int rank = ViewType1::rank> | |
| KOKKOS_INLINE_FUNCTION void | COPY (const ViewType1 &x, const ViewType2 &y) |
| Deep copy x into y, where x and y are either rank 1 (vectors) or rank 2 (matrices) with the same dimension(s). More... | |
| template<class VecType1 , class BlkType , class VecType2 , class CoeffType , class IndexType = int> | |
| KOKKOS_INLINE_FUNCTION void | GEMV (const CoeffType &alpha, const BlkType &A, const VecType1 &x, const VecType2 &y) |
y := y + alpha * A * x (dense matrix-vector multiply) More... | |
| template<class ViewType1 , class ViewType2 , class ViewType3 , class CoefficientType , class IndexType = int> | |
| KOKKOS_INLINE_FUNCTION void | GEMM (const char transA[], const char transB[], const CoefficientType &alpha, const ViewType1 &A, const ViewType2 &B, const CoefficientType &beta, const ViewType3 &C) |
Small dense matrix-matrix multiply: C := alpha*A*B + beta*C More... | |
| template<class LittleBlockType , class LittleVectorType > | |
| KOKKOS_INLINE_FUNCTION void | GETF2 (const LittleBlockType &A, const LittleVectorType &ipiv, int &info) |
| Computes A = P*L*U. More... | |
| template<class LittleBlockType , class LittleIntVectorType , class LittleScalarVectorType > | |
| KOKKOS_INLINE_FUNCTION void | GETRS (const char mode[], const LittleBlockType &A, const LittleIntVectorType &ipiv, const LittleScalarVectorType &B, int &info) |
| Solve the linear system(s) AX=B, using the result of GETRF or GETF2. More... | |
| template<class LittleBlockType , class LittleIntVectorType , class LittleScalarVectorType > | |
| KOKKOS_INLINE_FUNCTION void | GETRI (const LittleBlockType &A, const LittleIntVectorType &ipiv, const LittleScalarVectorType &work, int &info) |
| Compute inverse of A, using result of GETRF or GETF2. More... | |
| void | setCombineModeParameter (Teuchos::ParameterList &plist, const std::string ¶mName) |
| Set CombineMode parameter in a Teuchos::ParameterList. More... | |
| std::string | combineModeToString (const CombineMode combineMode) |
| Human-readable string representation of the given CombineMode. More... | |
| template<class SC , class LO , class GO , class NT > | |
| Details::EquilibrationInfo < typename Kokkos::ArithTraits < SC >::val_type, typename NT::device_type > | computeRowOneNorms (const Tpetra::RowMatrix< SC, LO, GO, NT > &A) |
| Compute global row one-norms ("row sums") of the input sparse matrix A, in a way suitable for one-sided (left only) equilibration. More... | |
| template<class SC , class LO , class GO , class NT > | |
| Details::EquilibrationInfo < typename Kokkos::ArithTraits < SC >::val_type, typename NT::device_type > | computeRowAndColumnOneNorms (const Tpetra::RowMatrix< SC, LO, GO, NT > &A, const bool assumeSymmetric) |
| Compute global row and column one-norms ("row sums" and "column sums") of the input sparse matrix A, in a way suitable for two-sided (left and right) equilibration. More... | |
| bool | isInitialized () |
| Whether Tpetra is in an initialized state. More... | |
| Teuchos::RCP< const Teuchos::Comm< int > > | getDefaultComm () |
| Get Tpetra's default communicator. More... | |
| void | initialize (int *argc, char ***argv) |
| Initialize Tpetra. More... | |
| void | initialize (int *argc, char ***argv, const Teuchos::RCP< const Teuchos::Comm< int > > &comm) |
| Initialize Tpetra. More... | |
| void | finalize () |
| Finalize Tpetra. More... | |
| template<class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP< CrsGraph < LocalOrdinal, GlobalOrdinal, Node > > | createCrsGraph (const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> &map, size_t maxNumEntriesPerRow=0, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) |
| Nonmember function to create an empty CrsGraph given a row Map and the max number of entries allowed locally per row. More... | |
| template<class CrsGraphType > | |
| Teuchos::RCP< CrsGraphType > | importAndFillCompleteCrsGraph (const Teuchos::RCP< const CrsGraphType > &sourceGraph, const Import< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type > &importer, const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> &domainMap=Teuchos::null, const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> &rangeMap=Teuchos::null, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) |
| Nonmember CrsGraph constructor that fuses Import and fillComplete(). More... | |
| template<class CrsGraphType > | |
| Teuchos::RCP< CrsGraphType > | importAndFillCompleteCrsGraph (const Teuchos::RCP< const CrsGraphType > &sourceGraph, const Import< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type > &rowImporter, const Import< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type > &domainImporter, const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> &domainMap, const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> &rangeMap, const Teuchos::RCP< Teuchos::ParameterList > ¶ms) |
| Nonmember CrsGraph constructor that fuses Import and fillComplete(). More... | |
| template<class CrsGraphType > | |
| Teuchos::RCP< CrsGraphType > | exportAndFillCompleteCrsGraph (const Teuchos::RCP< const CrsGraphType > &sourceGraph, const Export< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type > &exporter, const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> &domainMap=Teuchos::null, const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> &rangeMap=Teuchos::null, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) |
| Nonmember CrsGraph constructor that fuses Export and fillComplete(). More... | |
| template<class CrsGraphType > | |
| Teuchos::RCP< CrsGraphType > | exportAndFillCompleteCrsGraph (const Teuchos::RCP< const CrsGraphType > &sourceGraph, const Export< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type > &rowExporter, const Export< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type > &domainExporter, const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> &domainMap, const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> &rangeMap, const Teuchos::RCP< Teuchos::ParameterList > ¶ms) |
| Nonmember CrsGraph constructor that fuses Export and fillComplete(). More... | |
| template<class CrsMatrixType > | |
| Teuchos::RCP< CrsMatrixType > | importAndFillCompleteCrsMatrix (const Teuchos::RCP< const CrsMatrixType > &sourceMatrix, const Import< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > &importer, const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > &domainMap=Teuchos::null, const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > &rangeMap=Teuchos::null, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) |
| Nonmember CrsMatrix constructor that fuses Import and fillComplete(). More... | |
| template<class CrsMatrixType > | |
| Teuchos::RCP< CrsMatrixType > | importAndFillCompleteCrsMatrix (const Teuchos::RCP< const CrsMatrixType > &sourceMatrix, const Import< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > &rowImporter, const Import< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > &domainImporter, const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > &domainMap, const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > &rangeMap, const Teuchos::RCP< Teuchos::ParameterList > ¶ms) |
| Nonmember CrsMatrix constructor that fuses Import and fillComplete(). More... | |
| template<class CrsMatrixType > | |
| Teuchos::RCP< CrsMatrixType > | exportAndFillCompleteCrsMatrix (const Teuchos::RCP< const CrsMatrixType > &sourceMatrix, const Export< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > &exporter, const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > &domainMap=Teuchos::null, const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > &rangeMap=Teuchos::null, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) |
| Nonmember CrsMatrix constructor that fuses Export and fillComplete(). More... | |
| template<class CrsMatrixType > | |
| Teuchos::RCP< CrsMatrixType > | exportAndFillCompleteCrsMatrix (const Teuchos::RCP< const CrsMatrixType > &sourceMatrix, const Export< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > &rowExporter, const Export< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > &domainExporter, const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > &domainMap, const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > &rangeMap, const Teuchos::RCP< Teuchos::ParameterList > ¶ms) |
| Nonmember CrsMatrix constructor that fuses Export and fillComplete(). More... | |
| template<class Scalar , class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP< CrsMatrix < Scalar, LocalOrdinal, GlobalOrdinal, Node > > | createCrsMatrix (const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > &map, const size_t maxNumEntriesPerRow=0, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) |
| Create an empty CrsMatrix given a row map and a single integer upper bound on the number of stored entries per row. More... | |
| template<class CrsMatrixType > | |
| void | removeCrsMatrixZeros (CrsMatrixType &matrix, typename Teuchos::ScalarTraits< typename CrsMatrixType::scalar_type >::magnitudeType const &threshold=Teuchos::ScalarTraits< typename CrsMatrixType::scalar_type >::magnitude(Teuchos::ScalarTraits< typename CrsMatrixType::scalar_type >::zero())) |
| Remove zero entries from a matrix. More... | |
| template<class OpScalar , class MatScalar , class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP < CrsMatrixMultiplyOp < OpScalar, MatScalar, LocalOrdinal, GlobalOrdinal, Node > > | createCrsMatrixMultiplyOp (const Teuchos::RCP< const CrsMatrix< MatScalar, LocalOrdinal, GlobalOrdinal, Node > > &A) |
| Non-member function to create a CrsMatrixMultiplyOp. More... | |
| template<class DistObjectType > | |
| void | removeEmptyProcessesInPlace (Teuchos::RCP< DistObjectType > &input, const Teuchos::RCP< const Map< typename DistObjectType::local_ordinal_type, typename DistObjectType::global_ordinal_type, typename DistObjectType::node_type > > &newMap) |
| Remove processes which contain no elements in this object's Map. More... | |
| template<class DistObjectType > | |
| void | removeEmptyProcessesInPlace (Teuchos::RCP< DistObjectType > &input) |
| Remove processes which contain no elements in this object's Map. More... | |
| template<class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP< const Export < LocalOrdinal, GlobalOrdinal, Node > > | createExport (const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > &src, const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > &tgt) |
| Nonmember "constructor" for Export objects. More... | |
| template<class matrix_type , class filter_type > | |
| Teuchos::RCP< matrix_type > | applyFilter_vals (const matrix_type &A, const filter_type &filter) |
| Constructs a matrix consisting only of the entries for which the filter function evaluates to true. More... | |
| template<class matrix_type , class filter_type > | |
| Teuchos::RCP< matrix_type > | applyFilter_LID (const matrix_type &A, const filter_type &filter) |
| Constructs a matrix consisting only of the entries for which the filter function evaluates to true. More... | |
| template<class matrix_type , class filter_type > | |
| Teuchos::RCP< matrix_type > | applyFilter_GID (const matrix_type &A, const filter_type &filter) |
| Constructs a matrix consisting only of the entries for which the filter function evaluates to true. More... | |
| template<class SC , class LO , class GO , class NT > | |
| std::shared_ptr <::Tpetra::Details::CommRequest > | idot (typename::Tpetra::MultiVector< SC, LO, GO, NT >::dot_type *resultRaw, const ::Tpetra::MultiVector< SC, LO, GO, NT > &X, const ::Tpetra::MultiVector< SC, LO, GO, NT > &Y) |
| Nonblocking dot product, with either Tpetra::MultiVector or Tpetra::Vector inputs, and raw pointer or raw array output. More... | |
| template<class SC , class LO , class GO , class NT > | |
| std::shared_ptr <::Tpetra::Details::CommRequest > | idot (const Kokkos::View< typename::Tpetra::MultiVector< SC, LO, GO, NT >::dot_type *, typename::Tpetra::MultiVector< SC, LO, GO, NT >::device_type > &result, const ::Tpetra::MultiVector< SC, LO, GO, NT > &X, const ::Tpetra::MultiVector< SC, LO, GO, NT > &Y) |
| Nonblocking dot product, with Tpetra::MultiVector inputs, and rank-1 (one-dimensional array) Kokkos::View output. More... | |
| template<class SC , class LO , class GO , class NT > | |
| std::shared_ptr <::Tpetra::Details::CommRequest > | idot (const Kokkos::View< typename::Tpetra::Vector< SC, LO, GO, NT >::dot_type, typename::Tpetra::Vector< SC, LO, GO, NT >::device_type > &result, const ::Tpetra::Vector< SC, LO, GO, NT > &X, const ::Tpetra::Vector< SC, LO, GO, NT > &Y) |
| Nonblocking dot product, with Tpetra::Vector inputs, and rank-0 (single value) Kokkos::View output. More... | |
| template<class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP< const Import < LocalOrdinal, GlobalOrdinal, Node > > | createImport (const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> &src, const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> &tgt) |
| Nonmember constructor for Import. More... | |
| template<class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP< const Import < LocalOrdinal, GlobalOrdinal, Node > > | createImport (const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> &src, const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> &tgt, const Teuchos::RCP< Teuchos::ParameterList > &plist) |
| Nonmember constructor for Import that takes a ParameterList. More... | |
| template<class SC , class LO , class GO , class NT > | |
| void | leftAndOrRightScaleCrsMatrix (Tpetra::CrsMatrix< SC, LO, GO, NT > &A, const Kokkos::View< const typename Kokkos::ArithTraits< SC >::mag_type *, typename NT::device_type > &rowScalingFactors, const Kokkos::View< const typename Kokkos::ArithTraits< SC >::mag_type *, typename NT::device_type > &colScalingFactors, const bool leftScale, const bool rightScale, const bool assumeSymmetric, const EScaling scaling) |
| Left-scale and/or right-scale (in that order) the entries of the input Tpetra::CrsMatrix A. More... | |
| template<class SC , class LO , class GO , class NT > | |
| void | leftAndOrRightScaleCrsMatrix (Tpetra::CrsMatrix< SC, LO, GO, NT > &A, const Tpetra::Vector< typename Kokkos::ArithTraits< SC >::mag_type, LO, GO, NT > &rowScalingFactors, const Tpetra::Vector< typename Kokkos::ArithTraits< SC >::mag_type, LO, GO, NT > &colScalingFactors, const bool leftScale, const bool rightScale, const bool assumeSymmetric, const EScaling scaling) |
| Left-scale and/or right-scale (in that order) the entries of the input Tpetra::CrsMatrix A. More... | |
| template<class LocalOrdinal , class GlobalOrdinal > | |
| Teuchos::RCP< const Map < LocalOrdinal, GlobalOrdinal > > | createLocalMap (const size_t numElements, const Teuchos::RCP< const Teuchos::Comm< int >> &comm) |
| Nonmember constructor for a locally replicated Map with the default Kokkos Node. More... | |
| template<class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP< const Map < LocalOrdinal, GlobalOrdinal, Node > > | createLocalMapWithNode (const size_t numElements, const Teuchos::RCP< const Teuchos::Comm< int >> &comm) |
| Nonmember constructor for a locally replicated Map with a specified Kokkos Node. More... | |
| template<class LocalOrdinal , class GlobalOrdinal > | |
| Teuchos::RCP< const Map < LocalOrdinal, GlobalOrdinal > > | createUniformContigMap (const global_size_t numElements, const Teuchos::RCP< const Teuchos::Comm< int >> &comm) |
| Non-member constructor for a uniformly distributed, contiguous Map with the default Kokkos Node. More... | |
| template<class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP< const Map < LocalOrdinal, GlobalOrdinal, Node > > | createUniformContigMapWithNode (const global_size_t numElements, const Teuchos::RCP< const Teuchos::Comm< int >> &comm) |
| Non-member constructor for a uniformly distributed, contiguous Map with a user-specified Kokkos Node. More... | |
| template<class LocalOrdinal , class GlobalOrdinal > | |
| Teuchos::RCP< const Map < LocalOrdinal, GlobalOrdinal > > | createContigMap (const global_size_t numElements, const size_t localNumElements, const Teuchos::RCP< const Teuchos::Comm< int >> &comm) |
| Non-member constructor for a (potentially) non-uniformly distributed, contiguous Map using the default Kokkos::Device. More... | |
| template<class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP< const Map < LocalOrdinal, GlobalOrdinal, Node > > | createContigMapWithNode (const global_size_t numElements, const size_t localNumElements, const Teuchos::RCP< const Teuchos::Comm< int >> &comm) |
| Nonmember constructor for a (potentially) nonuniformly distributed, contiguous Map for a user-specified, possibly nondefault Kokkos Node type. More... | |
| template<class LocalOrdinal , class GlobalOrdinal > | |
| Teuchos::RCP< const Map < LocalOrdinal, GlobalOrdinal > > | createNonContigMap (const Teuchos::ArrayView< const GlobalOrdinal > &elementList, const Teuchos::RCP< const Teuchos::Comm< int >> &comm) |
| Nonmember constructor for a non-contiguous Map using the default Kokkos::Device type. More... | |
| template<class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP< const Map < LocalOrdinal, GlobalOrdinal, Node > > | createNonContigMapWithNode (const Teuchos::ArrayView< const GlobalOrdinal > &elementList, const Teuchos::RCP< const Teuchos::Comm< int >> &comm) |
| Nonmember constructor for a noncontiguous Map with a user-specified, possibly nondefault Kokkos Node type. More... | |
| template<class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP< const Map < LocalOrdinal, GlobalOrdinal, Node > > | createOneToOne (const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> &M) |
| Nonmember constructor for a contiguous Map with user-defined weights and a user-specified, possibly nondefault Kokkos Node type. More... | |
| template<class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP< const Map < LocalOrdinal, GlobalOrdinal, Node > > | createOneToOne (const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> &M, const ::Tpetra::Details::TieBreak< LocalOrdinal, GlobalOrdinal > &tie_break) |
| Creates a one-to-one version of the given Map where each GID lives on only one process. The given TieBreak object specifies the rule to break ties. More... | |
| template<class Scalar , class OpScalar , class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP < MixedScalarMultiplyOp < Scalar, OpScalar, LocalOrdinal, GlobalOrdinal, Node > > | createMixedScalarMultiplyOp (const Teuchos::RCP< const Operator< OpScalar, LocalOrdinal, GlobalOrdinal, Node > > &A) |
| Non-member function to create a MixedScalarMultiplyOp. More... | |
| template<class DS , class DL , class DG , class DN , class SS , class SL , class SG , class SN > | |
| void | deep_copy (MultiVector< DS, DL, DG, DN > &dst, const MultiVector< SS, SL, SG, SN > &src) |
Copy the contents of the MultiVector src into dst. More... | |
| template<class ST , class LO , class GO , class NT > | |
| MultiVector< ST, LO, GO, NT > | createCopy (const MultiVector< ST, LO, GO, NT > &src) |
| Return a deep copy of the given MultiVector. More... | |
| template<class Scalar , class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP< MultiVector < Scalar, LocalOrdinal, GlobalOrdinal, Node > > | createMultiVector (const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> &map, const size_t numVectors) |
| Nonmember MultiVector "constructor": Create a MultiVector from a given Map. More... | |
| template<class ST , class LO , class GO , class NT > | |
| void | deep_copy (MultiVector< ST, LO, GO, NT > &dst, const MultiVector< ST, LO, GO, NT > &src) |
| Specialization of deep_copy for MultiVector objects with the same template parameters. More... | |
| template<class SC , class LO , class GO , class NT > | |
| LO | replaceDiagonalCrsMatrix (::Tpetra::CrsMatrix< SC, LO, GO, NT > &matrix, const ::Tpetra::Vector< SC, LO, GO, NT > &newDiag) |
Replace diagonal entries of an input Tpetra::CrsMatrix matrix with values given in newDiag. More... | |
| template<typename MapType , typename KeyArgType , typename ValueArgType > | |
| MapType::iterator | efficientAddOrUpdate (MapType &m, const KeyArgType &k, const ValueArgType &v) |
| Efficiently insert or replace an entry in an std::map. More... | |
| template<class IT1 , class IT2 > | |
| void | sort2 (const IT1 &first1, const IT1 &last1, const IT2 &first2, const bool stableSort=false) |
| Sort the first array, and apply the resulting permutation to the second array. More... | |
| template<class View1 , class View2 > | |
| void | sort2 (View1 &view1, const size_t &size, View2 &view2) |
| Sort the first array, and apply the resulting permutation to the second array. More... | |
| template<class View > | |
| void | sort (View &view, const size_t &size) |
| Convenience wrapper for std::sort for host-accessible views. More... | |
| template<class View > | |
| void | reverse_sort (View &view, const size_t &size) |
| Convenience wrapper for a reversed std::sort for host-accessible views. More... | |
| template<class IT1 , class IT2 , class IT3 > | |
| void | sort3 (const IT1 &first1, const IT1 &last1, const IT2 &first2, const IT3 &first3, const bool stableSort=false) |
| Sort the first array, and apply the same permutation to the second and third arrays. More... | |
| template<class IT1 , class IT2 > | |
| void | merge2 (IT1 &indResultOut, IT2 &valResultOut, IT1 indBeg, IT1 indEnd, IT2 valBeg, IT2) |
| Merge values in place, additively, with the same index. More... | |
| template<class IT1 , class IT2 , class BinaryFunction > | |
| void | merge2 (IT1 &indResultOut, IT2 &valResultOut, IT1 indBeg, IT1 indEnd, IT2 valBeg, IT2 valEnd, BinaryFunction f) |
| Merge values in place with the same index, using any associative binary function. More... | |
| template<class KeyInputIterType , class ValueInputIterType , class KeyOutputIterType , class ValueOutputIterType , class BinaryFunction > | |
| void | keyValueMerge (KeyInputIterType keyBeg1, KeyInputIterType keyEnd1, ValueInputIterType valBeg1, ValueInputIterType valEnd1, KeyInputIterType keyBeg2, KeyInputIterType keyEnd2, ValueInputIterType valBeg2, ValueInputIterType valEnd2, KeyOutputIterType keyOut, ValueOutputIterType valOut, BinaryFunction f) |
| Merge two sorted (by keys) sequences of unique (key,value) pairs by combining pairs with equal keys. More... | |
| template<class Scalar , class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > | createCopy (const Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &src) |
| Return a deep copy of the given Vector. More... | |
| template<class Scalar , class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP< Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > | createVector (const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > &map) |
| Nonmember Vector "constructor": Create a Vector from a given Map. More... | |
Methods performing multiple matrix-vector products at once | |
| template<class MatrixArray , class MultiVectorArray > | |
| void | batchedApply (const MatrixArray &Matrices, const typename std::remove_pointer< typename MultiVectorArray::value_type >::type &X, MultiVectorArray &Y, typename std::remove_pointer< typename MatrixArray::value_type >::type::scalar_type alpha=Teuchos::ScalarTraits< typename std::remove_pointer< typename MatrixArray::value_type >::type::scalar_type >::one(), typename std::remove_pointer< typename MatrixArray::value_type >::type::scalar_type beta=Teuchos::ScalarTraits< typename std::remove_pointer< typename MatrixArray::value_type >::type::scalar_type >::zero(), Teuchos::RCP< Teuchos::ParameterList > params=Teuchos::null) |
| Does multiply matrix apply() calls with a single X vector. More... | |
Namespace Tpetra contains the class and methods constituting the Tpetra library.
Namespace for Tpetra classes and methods.
| typedef Teuchos_Ordinal Tpetra::Array_size_type |
Size type for Teuchos Array objects.
Definition at line 21 of file Tpetra_ConfigDefs.hpp.
| typedef size_t Tpetra::global_size_t |
Global size_t object.
This type is intended to support scenarios where the global memory allocation is larger than that of a single node.
Currently, it is typedefed to size_t.
Definition at line 70 of file Tpetra_ConfigDefs.hpp.
| enum Tpetra::CombineMode |
Rule for combining data in an Import or Export.
Import or Export (data redistribution) operations might need to combine data received from other processes with existing data on the calling process. This enum tells Tpetra how to do that for a specific Import or Export operation. Each Tpetra object may interpret the CombineMode in a different way, so you should check the Tpetra object's documentation for details.
Here is the list of supported combine modes:
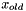 is the old value and
is the old value and  the incoming new value, replace
the incoming new value, replace 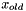 with
with 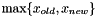 .
.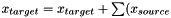 May not be supported in all classes
May not be supported in all classesADD, REPLACE and ADD_ASSIGN are intended for modifying values that already exist. Tpetra objects will generally work correctly if those values don't already exist. (For example, ADD will behave like INSERT if the entry does not yet exist on the calling process.) However, performance may suffer.
The ZERO combine mode is a special case that bypasses communication. It may seem odd to include a "combine mode" that doesn't actually combine. However, this is useful for computations like domain decomposition with overlap. A ZERO combine mode with overlap is different than an ADD combine mode without overlap. (See Ifpack2::AdditiveSchwarz, which inspired inclusion of this combine mode.) Furthermore, Import and Export also encapsulate a local permutation; if you want only to execute the local permutation without communication, you may use the ZERO combine mode.
Definition at line 65 of file Tpetra_CombineMode.hpp.
| enum Tpetra::LocalGlobal |
Enum for local versus global allocation of Map entries.
LocallyReplicated means that the Map's entries are locally replicated across all processes.
GloballyDistributed means that the Map's entries are globally distributed across all processes.
Definition at line 79 of file Tpetra_ConfigDefs.hpp.
| enum Tpetra::LookupStatus |
Return status of Map remote index lookup (getRemoteIndexList()).
| Enumerator | |
|---|---|
| AllIDsPresent |
All queried indices were present in the Map |
| IDNotPresent |
At least one of the specified indices was not present in the Map |
Definition at line 85 of file Tpetra_ConfigDefs.hpp.
Optimize storage option
| Enumerator | |
|---|---|
| DoOptimizeStorage |
Indicates that storage should be optimized |
| DoNotOptimizeStorage |
Indicates that storage should not be optimized |
Definition at line 91 of file Tpetra_ConfigDefs.hpp.
Sweep direction for Gauss-Seidel or Successive Over-Relaxation (SOR).
Definition at line 192 of file Tpetra_ConfigDefs.hpp.
| enum Tpetra::EScaling |
Whether "scaling" a matrix means multiplying or dividing its entries.
leftAndOrRightScaleCrsMatrix (see below) takes this as input.
Definition at line 32 of file Tpetra_leftAndOrRightScaleCrsMatrix_decl.hpp.
| void Tpetra::batchedApply | ( | const MatrixArray & | Matrices, |
| const typename std::remove_pointer< typename MultiVectorArray::value_type >::type & | X, | ||
| MultiVectorArray & | Y, | ||
| typename std::remove_pointer< typename MatrixArray::value_type >::type::scalar_type | alpha = Teuchos::ScalarTraits<typename std::remove_pointer<typename MatrixArray::value_type>::type::scalar_type>::one(), |
||
| typename std::remove_pointer< typename MatrixArray::value_type >::type::scalar_type | beta = Teuchos::ScalarTraits<typename std::remove_pointer<typename MatrixArray::value_type>::type::scalar_type>::zero(), |
||
| Teuchos::RCP< Teuchos::ParameterList > | params = Teuchos::null |
||
| ) |
Does multiply matrix apply() calls with a single X vector.
Computes Y[i] = beta*Y[i] + alpha * Matrices[i] * X, for i=1,...,N
This routine only communicates the interprocessor portions of X once, if such a thing is possible (aka the ColMap's of the matrices match).
If the Y's are replicated this will not use the reduced communication path.
If X is aliased to any Y but the last one, this routine will throw
| Matrices | [in] - [std::vector|Teuchos::Array|Teuchos::ArrayRCP] of Tpetra::CrsMatrix objects. These matrices can different numbers of rows. |
| X | [in] - Tpetra::MultiVector or Tpetra::Vector object. |
| Y | [out] - [std::vector|Teuchos::Array|Teuchos::ArrayRCP] of Tpetra::MultiVector or Tpetra::Vector objects. These must have the same number of vectors as X. |
| alpha | [in] - alpha parameter. Defaults to one. |
| beta | [in] - beta parameter. Defaults to zero. |
| params | [in/out] - The "can batch" parameter can either be unset, be true or be false on input. If it is unset, maps will be checked with isSameAs() for compatibility. If true, the map check will be skipped and batching will be used if none of the cheap checks fail. If false, batching will not be used. This parameter will be set on output to either true or false depending on if batching was used during this call. Defaults to NULL. |
Definition at line 44 of file Tpetra_Apply_Helpers.hpp.
| void Tpetra::applyDirichletBoundaryConditionToLocalMatrixRows | ( | const typename CrsMatrixType::execution_space & | execSpace, |
| CrsMatrixType & | A, | ||
| const Kokkos::View< typename CrsMatrixType::local_ordinal_type *, typename CrsMatrixType::device_type > & | lclRowInds | ||
| ) |
For all k in [0, lclRowInds.extent(0)), set local row lclRowInds[k] of A to have 1 on the diagonal and 0 elsewhere. Run on device.
| CrsMatrixType | Specialization of Tpetra::CrsMatrix. |
| execSpace | [in] Execution space instance on which to run. |
| A | [in/out] Sparse matrix to modify. |
| lclRowInds | [in] Local indices of the rows of A to modify. |
Definition at line 365 of file Tpetra_applyDirichletBoundaryCondition.hpp.
| void Tpetra::applyDirichletBoundaryConditionToLocalMatrixRows | ( | CrsMatrixType & | A, |
| const Kokkos::View< typename CrsMatrixType::local_ordinal_type *, typename CrsMatrixType::device_type > & | lclRowInds | ||
| ) |
For all k in [0, lclRowInds.extent(0)), set local row lclRowInds[k] of A to have 1 on the diagonal and 0 elsewhere. Run on device, using the default execution space instance.
| CrsMatrixType | Specialization of Tpetra::CrsMatrix. |
| A | [in/out] Sparse matrix to modify. |
| lclRowInds | [in] Local indices of the rows of A to modify. |
Definition at line 387 of file Tpetra_applyDirichletBoundaryCondition.hpp.
| void Tpetra::applyDirichletBoundaryConditionToLocalMatrixRows | ( | CrsMatrixType & | A, |
| const Kokkos::View< typename CrsMatrixType::local_ordinal_type *, Kokkos::HostSpace > & | lclRowInds | ||
| ) |
For all k in [0, lclRowInds.extent(0)), set local row lclRowInds[k] of A to have 1 on the diagonal and 0 elsewhere. Run on host, using the default host execution space instance.
| CrsMatrixType | Specialization of Tpetra::CrsMatrix. |
| A | [in/out] Sparse matrix to modify. |
| lclRowInds | [in] Local indices of the rows of A to modify. |
Definition at line 396 of file Tpetra_applyDirichletBoundaryCondition.hpp.
| void Tpetra::applyDirichletBoundaryConditionToLocalMatrixRowsAndColumns | ( | const typename CrsMatrixType::execution_space & | execSpace, |
| CrsMatrixType & | A, | ||
| const Kokkos::View< typename CrsMatrixType::local_ordinal_type *, typename CrsMatrixType::device_type > & | lclRowInds | ||
| ) |
For all k in [0, lclRowInds.extent(0)), set local row and column lclRowInds[k] of A to have 1 on the diagonal and 0 elsewhere. Run on host, using the default host execution space instance.
| CrsMatrixType | Specialization of Tpetra::CrsMatrix. |
| A | [in/out] Sparse matrix to modify. |
| lclRowInds | [in] Local indices of the rows of A to modify. |
Definition at line 474 of file Tpetra_applyDirichletBoundaryCondition.hpp.
| void Tpetra::applyDirichletBoundaryConditionToLocalMatrixRowsAndColumns | ( | CrsMatrixType & | A, |
| const Kokkos::View< typename CrsMatrixType::local_ordinal_type *, Kokkos::HostSpace > & | lclRowInds | ||
| ) |
For all k in [0, lclRowInds.extent(0)), set local row and column lclRowInds[k] of A to have 1 on the diagonal and 0 elsewhere. Run on host, using the default host execution space instance.
| CrsMatrixType | Specialization of Tpetra::CrsMatrix. |
| A | [in/out] Sparse matrix to modify. |
| lclRowInds | [in] Local indices of the rows of A to modify. |
Definition at line 425 of file Tpetra_applyDirichletBoundaryCondition.hpp.
| void Tpetra::applyDirichletBoundaryConditionToLocalMatrixRowsAndColumns | ( | CrsMatrixType & | A, |
| const Kokkos::View< typename CrsMatrixType::local_ordinal_type *, typename CrsMatrixType::device_type > & | lclRowInds | ||
| ) |
For all k in [0, lclRowInds.extent(0)), set local row and column lclRowInds[k] of A to have 1 on the diagonal and 0 elsewhere. Run on host, using the default host execution space instance.
| CrsMatrixType | Specialization of Tpetra::CrsMatrix. |
| A | [in/out] Sparse matrix to modify. |
| lclRowInds | [in] Local indices of the rows of A to modify. |
Definition at line 451 of file Tpetra_applyDirichletBoundaryCondition.hpp.
| void Tpetra::blockCrsMatrixWriter | ( | BlockCrsMatrix< Scalar, LO, GO, Node > const & | A, |
| std::string const & | fileName | ||
| ) |
Helper function to write a BlockCrsMatrix. Calls the 3-argument version.
Definition at line 29 of file Tpetra_BlockCrsMatrix_Helpers_def.hpp.
| void Tpetra::blockCrsMatrixWriter | ( | BlockCrsMatrix< Scalar, LO, GO, Node > const & | A, |
| std::string const & | fileName, | ||
| Teuchos::ParameterList const & | params | ||
| ) |
Helper function to write a BlockCrsMatrix. Calls the 3-argument version.
Definition at line 37 of file Tpetra_BlockCrsMatrix_Helpers_def.hpp.
| void Tpetra::blockCrsMatrixWriter | ( | BlockCrsMatrix< Scalar, LO, GO, Node > const & | A, |
| std::ostream & | os | ||
| ) |
Helper function to write a BlockCrsMatrix. Calls the 3-argument version.
Definition at line 44 of file Tpetra_BlockCrsMatrix_Helpers_def.hpp.
| void Tpetra::blockCrsMatrixWriter | ( | BlockCrsMatrix< Scalar, LO, GO, Node > const & | A, |
| std::ostream & | os, | ||
| Teuchos::ParameterList const & | params | ||
| ) |
Helper function to write a BlockCrsMatrix.
Writes the block matrix to the specified ostream in point form. The following parameter list options are available:
Definition at line 50 of file Tpetra_BlockCrsMatrix_Helpers_def.hpp.
| void Tpetra::writeMatrixStrip | ( | BlockCrsMatrix< Scalar, LO, GO, Node > const & | A, |
| std::ostream & | os, | ||
| Teuchos::ParameterList const & | params | ||
| ) |
Helper function called by blockCrsMatrixWriter.
This function should not be called directly.
Definition at line 166 of file Tpetra_BlockCrsMatrix_Helpers_def.hpp.
| Teuchos::RCP< Tpetra::CrsGraph< LO, GO, Node > > Tpetra::getBlockCrsGraph | ( | const Tpetra::CrsMatrix< Scalar, LO, GO, Node > & | pointMatrix, |
| const LO & | blockSize, | ||
| bool | use_local_ID = true |
||
| ) |
Non-member constructor that creates the CrsGraph of a BlockCrsMatrix from an existing point CrsMatrix and a block size.
This function accepts an already constructed point version of the block matrix. Assumptions:
Definition at line 260 of file Tpetra_BlockCrsMatrix_Helpers_def.hpp.
| Teuchos::RCP< BlockCrsMatrix< Scalar, LO, GO, Node > > Tpetra::convertToBlockCrsMatrix | ( | const Tpetra::CrsMatrix< Scalar, LO, GO, Node > & | pointMatrix, |
| const LO & | blockSize, | ||
| bool | use_local_ID = true |
||
| ) |
Non-member constructor that creates a BlockCrsMatrix from an existing point CrsMatrix.
This function accepts an already constructed point version of the block matrix. Assumptions:
Definition at line 401 of file Tpetra_BlockCrsMatrix_Helpers_def.hpp.
| Teuchos::RCP< Tpetra::CrsMatrix< Scalar, LO, GO, Node > > Tpetra::fillLogicalBlocks | ( | const Tpetra::CrsMatrix< Scalar, LO, GO, Node > & | pointMatrix, |
| const LO & | blockSize | ||
| ) |
Fill all point entries in a logical block of a CrsMatrix with zeroes. This should be called before convertToBlockCrsMatrix if your Crs is not filled. Performed on host.
This function accepts an already constructed point version of the block matrix. Assumptions:
Definition at line 529 of file Tpetra_BlockCrsMatrix_Helpers_def.hpp.
| Teuchos::RCP< Tpetra::CrsMatrix< Scalar, LO, GO, Node > > Tpetra::unfillFormerBlockCrs | ( | const Tpetra::CrsMatrix< Scalar, LO, GO, Node > & | pointMatrix | ) |
Unfill all point entries in a logical block of a CrsMatrix with zeroes. This can be called after convertToCrsMatrix if you don't want to keep the filled values. Performed on host.
This function accepts an already constructed point version of the block matrix. It is expected that, given a crs A Afill = fillLogicalBlocks(A) Abcrs = convertToBlockCrsMatrix(Afill) Acrs = convertToCrsMatrix(Abcrs); Aorig = unfillFormerBlockCrs(Acrs); Expect A and Aorig are identical Assumptions:
Definition at line 812 of file Tpetra_BlockCrsMatrix_Helpers_def.hpp.
| Teuchos::RCP< const Tpetra::Map< LO, GO, Node > > Tpetra::createMeshMap | ( | LO const & | blockSize, |
| const Tpetra::Map< LO, GO, Node > & | pointMap, | ||
| bool | use_local_ID = false |
||
| ) |
Helper function to generate a mesh map from a point map. Important! It's assumed that point GIDs associated with a single mesh GID appear consecutively in pointMap.
Definition at line 885 of file Tpetra_BlockCrsMatrix_Helpers_def.hpp.
| Teuchos::RCP< CrsMatrix< Scalar, LO, GO, Node > > Tpetra::convertToCrsMatrix | ( | const Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node > & | blockMatrix | ) |
Non-member constructor that creates a point CrsMatrix from an existing BlockCrsMatrix.
This function accepts an already constructed block matrix.
Definition at line 951 of file Tpetra_BlockCrsMatrix_Helpers_def.hpp.
| Teuchos::RCP< const Tpetra::Map< LO, GO, Node > > Tpetra::createPointMap | ( | LO const & | blockSize, |
| const Tpetra::Map< LO, GO, Node > & | blockMap | ||
| ) |
Helper function to generate a point map from a block map (with a given block size) GIDs associated with a single mesh GID appear consecutively in the output map.
Definition at line 930 of file Tpetra_BlockCrsMatrix_Helpers_def.hpp.
| KOKKOS_INLINE_FUNCTION void Tpetra::SCAL | ( | const CoefficientType & | alpha, |
| const ViewType & | x | ||
| ) |
x := alpha*x, where x is either rank 1 (a vector) or rank 2 (a matrix).
Definition at line 575 of file Tpetra_BlockView.hpp.
| KOKKOS_INLINE_FUNCTION void Tpetra::FILL | ( | const ViewType & | x, |
| const InputType & | val | ||
| ) |
Set every entry of x to val.
Definition at line 588 of file Tpetra_BlockView.hpp.
| KOKKOS_INLINE_FUNCTION void Tpetra::AXPY | ( | const CoefficientType & | alpha, |
| const ViewType1 & | x, | ||
| const ViewType2 & | y | ||
| ) |
y := y + alpha * x (dense vector or matrix update)
This function follows the BLAS convention that if alpha == 0, then it does nothing. (This matters only if x contains Inf or NaN values.)
Definition at line 606 of file Tpetra_BlockView.hpp.
| KOKKOS_INLINE_FUNCTION void Tpetra::COPY | ( | const ViewType1 & | x, |
| const ViewType2 & | y | ||
| ) |
Deep copy x into y, where x and y are either rank 1 (vectors) or rank 2 (matrices) with the same dimension(s).
| x | [in] The input vector / matrix. |
| y | [out] The output vector / matrix. |
We put the output argument last, because that's what the BLAS functions _COPY (replace _ with "S", "D", "C", or "Z") do.
Definition at line 634 of file Tpetra_BlockView.hpp.
| KOKKOS_INLINE_FUNCTION void Tpetra::GEMV | ( | const CoeffType & | alpha, |
| const BlkType & | A, | ||
| const VecType1 & | x, | ||
| const VecType2 & | y | ||
| ) |
y := y + alpha * A * x (dense matrix-vector multiply)
| alpha | [in] Coefficient by which to multiply A*x (this does NOT necessarily follow BLAS rules; the caller is responsible for checking whether alpha == 0 and implementing BLAS rules in that case). |
| A | [in] Small dense matrix (must have rank 2) |
| x | [in] Small dense vector input (must have rank 1 and at least as many rows as A has columns) |
| y | [in/out] Small dense vector output (must have rank 1 and at least as many rows as A has rows) |
Definition at line 664 of file Tpetra_BlockView.hpp.
| KOKKOS_INLINE_FUNCTION void Tpetra::GEMM | ( | const char | transA[], |
| const char | transB[], | ||
| const CoefficientType & | alpha, | ||
| const ViewType1 & | A, | ||
| const ViewType2 & | B, | ||
| const CoefficientType & | beta, | ||
| const ViewType3 & | C | ||
| ) |
Small dense matrix-matrix multiply: C := alpha*A*B + beta*C
| ViewType1 | Type of the first matrix input A. |
| ViewType2 | Type of the second matrix input B. |
| ViewType3 | Type of the third matrix input/output C. |
| CoefficientType | Type of the scalar coefficients alpha and beta. |
| IndexType | Type of the index used in for loops; defaults to int. |
Definition at line 691 of file Tpetra_BlockView.hpp.
| KOKKOS_INLINE_FUNCTION void Tpetra::GETF2 | ( | const LittleBlockType & | A, |
| const LittleVectorType & | ipiv, | ||
| int & | info | ||
| ) |
Computes A = P*L*U.
Definition at line 824 of file Tpetra_BlockView.hpp.
| KOKKOS_INLINE_FUNCTION void Tpetra::GETRS | ( | const char | mode[], |
| const LittleBlockType & | A, | ||
| const LittleIntVectorType & | ipiv, | ||
| const LittleScalarVectorType & | B, | ||
| int & | info | ||
| ) |
Solve the linear system(s) AX=B, using the result of GETRF or GETF2.
Definition at line 1054 of file Tpetra_BlockView.hpp.
| KOKKOS_INLINE_FUNCTION void Tpetra::GETRI | ( | const LittleBlockType & | A, |
| const LittleIntVectorType & | ipiv, | ||
| const LittleScalarVectorType & | work, | ||
| int & | info | ||
| ) |
Compute inverse of A, using result of GETRF or GETF2.
| LittleBlockType | Type of dense matrix A |
| LittleBlockType | Type of 1-D pivot array ipiv |
| LittleScalarVectorType | Type of 1-D work array work |
| A | [in/out] On input: output matrix resulting from running GETRF or GETF2 on a square matrix A. On output: inverse of the original matrix A. |
| ipiv | [in] Pivot array from the LU factorization. |
| work | [out] Temporary workspace; must be at least as long as the number of rows in A. |
| info | [out] On output, 0 if the routine was successful, else nonzero. |
Definition at line 1081 of file Tpetra_BlockView.hpp.
| void Tpetra::setCombineModeParameter | ( | Teuchos::ParameterList & | plist, |
| const std::string & | paramName | ||
| ) |
Set CombineMode parameter in a Teuchos::ParameterList.
If you are constructing a Teuchos::ParameterList with a CombineMode parameter, set the parameter by using this function. This will use a special feature of Teuchos – custom parameter list validation – so that users can specify CombineMode values by string, rather than enum value. The strings are the same as the enum names: "ADD", "INSERT", "REPLACE", "ABSMAX", and "ZERO". They are not case sensitive.
Using this function to set a CombineMode parameter will ensure that the XML serialization of the resulting Teuchos::ParameterList will refer to the CombineMode enum values using human-readable string names, rather than raw integers.
| plist | [out] Teuchos::ParameterList to which you want to add the Tpetra::CombineMode parameter. |
| paramName | [in] String name to use for the parameter. For example, you might wish to call the parameter "Combine Mode", "Tpetra::CombineMode", or "combine mode". The parameter's name is case sensitive, even though the string values are not. |
Definition at line 15 of file Tpetra_CombineMode.cpp.
| std::string Tpetra::combineModeToString | ( | const CombineMode | combineMode | ) |
Human-readable string representation of the given CombineMode.
Definition at line 61 of file Tpetra_CombineMode.cpp.
| Details::EquilibrationInfo< typename Kokkos::ArithTraits< SC >::val_type, typename NT::device_type > Tpetra::computeRowOneNorms | ( | const Tpetra::RowMatrix< SC, LO, GO, NT > & | A | ) |
Compute global row one-norms ("row sums") of the input sparse matrix A, in a way suitable for one-sided (left only) equilibration.
| A | [in] The input sparse matrix A. |
Definition at line 1138 of file Tpetra_computeRowAndColumnOneNorms_def.hpp.
| Details::EquilibrationInfo< typename Kokkos::ArithTraits< SC >::val_type, typename NT::device_type > Tpetra::computeRowAndColumnOneNorms | ( | const Tpetra::RowMatrix< SC, LO, GO, NT > & | A, |
| const bool | assumeSymmetric | ||
| ) |
Compute global row and column one-norms ("row sums" and "column sums") of the input sparse matrix A, in a way suitable for two-sided (left and right) equilibration.
AZ_scaling option to AZ_sym_row_sum.For the nonsymmetric case, this function works like a sparse version of LAPACK's DGEEQU routine, except that it uses one norms (sums of absolute values) instead of infinity norms (maximum absolute value). The resulting row and column scaling is NOT symmetric. For the symmetric case, this function computes the row norms and uses those for the column norms. The resulting scaling is symmetric IF you take square roots.
| A | [in] The input sparse matrix A. |
| assumeSymmetric | [in] Whether to assume that the matrix A is (globally) symmetric. If so, don't compute row-scaled column norms separately from row norms. |
Definition at line 1154 of file Tpetra_computeRowAndColumnOneNorms_def.hpp.
| bool Tpetra::isInitialized | ( | ) |
Whether Tpetra is in an initialized state.
Initialize Tpetra by calling one of the versions of initialize(). After initialize() returns, Tpetra is initialized. Once finalize() returns, Tpetra is no longer initialized.
Definition at line 166 of file Tpetra_Core.cpp.
| Teuchos::RCP< const Teuchos::Comm< int > > Tpetra::getDefaultComm | ( | ) |
Get Tpetra's default communicator.
Definition at line 170 of file Tpetra_Core.cpp.
| void Tpetra::initialize | ( | int * | argc, |
| char *** | argv | ||
| ) |
Initialize Tpetra.
This initializes the following if they have not already been initialized:
If Trilinos was built with MPI enabled, this function sets the default communicator to MPI_COMM_WORLD (wrapped in a Teuchos wrapper). Otherwise, it sets the default communicator to a Teuchos::SerialComm instance.
| argc | [in/out] Same as first argument of MPI_Init() |
| argv | [in/out] Same as second argument of MPI_Init() |
The argc and argv arguments are both passed by pointer, in order to match MPI_Init's interface. MPI_Init() reserves the right to modify command-line arguments, e.g., by reading and removing those that pertain to MPI. Thus, in main(), one would write
Definition at line 197 of file Tpetra_Core.cpp.
| void Tpetra::initialize | ( | int * | argc, |
| char *** | argv, | ||
| const Teuchos::RCP< const Teuchos::Comm< int > > & | comm | ||
| ) |
Initialize Tpetra.
This initializes the following if they have not already been initialized:
| argc | [in/out] Same as first argument of MPI_Init() |
| argv | [in/out] Same as second argument of MPI_Init() |
| comm | [in] Tpetra's default communicator, wrapped in a Teuchos wrapper. This may be either a Teuchos::MpiComm or a Teuchos::SerialComm instance. |
The argc and argv arguments are both passed by pointer, in order to match MPI_Init's interface. MPI_Init() reserves the right to modify command-line arguments, e.g., by reading and removing those that pertain to MPI. Thus, in main(), one would write
Definition at line 269 of file Tpetra_Core.cpp.
| void Tpetra::finalize | ( | ) |
Finalize Tpetra.
If Tpetra::initialize initialized Kokkos, finalize Kokkos. If Tpetra::initialize initialized MPI, finalize MPI. Don't call this unless you first call Tpetra::initialize.
If you (the user) initialized Kokkos resp. MPI before Tpetra::initialize was called, then this function does NOT finalize Kokkos resp. MPI. In that case, you (the user) are responsible for finalizing Kokkos resp. MPI.
Definition at line 292 of file Tpetra_Core.cpp.
| Teuchos::RCP< CrsGraph< LocalOrdinal, GlobalOrdinal, Node > > createCrsGraph | ( | const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> & | map, |
| size_t | maxNumEntriesPerRow = 0, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Nonmember function to create an empty CrsGraph given a row Map and the max number of entries allowed locally per row.
Definition at line 2524 of file Tpetra_CrsGraph_decl.hpp.
| Teuchos::RCP< CrsGraphType > importAndFillCompleteCrsGraph | ( | const Teuchos::RCP< const CrsGraphType > & | sourceGraph, |
| const Import< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type > & | importer, | ||
| const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> & | domainMap = Teuchos::null, |
||
| const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> & | rangeMap = Teuchos::null, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Nonmember CrsGraph constructor that fuses Import and fillComplete().
| CrsGraphType | A specialization of CrsGraph. |
A common use case is to create an empty destination CrsGraph, redistribute from a source CrsGraph (by an Import or Export operation), then call fillComplete() on the destination CrsGraph. This constructor fuses these three cases, for an Import redistribution.
Fusing redistribution and fillComplete() exposes potential optimizations. For example, it may make constructing the column Map faster, and it may avoid intermediate unoptimized storage in the destination CrsGraph.
The resulting graph is fill complete (in the sense of isFillComplete()) and has optimized storage (in the sense of isStorageOptimized()). By default, its domain Map is the domain Map of the source graph, and its range Map is the range Map of the source graph.
| sourceGraph | [in] The source graph from which to import. The source of an Import must have a nonoverlapping distribution. |
| importer | [in] The Import instance containing a precomputed redistribution plan. The source Map of the Import must be the same as the rowMap of sourceGraph unless the "Reverse Mode" option on the params list, in which case the targetMap of Import must match the rowMap of the sourceGraph |
| domainMap | [in] Domain Map of the returned graph. If null, we use the default, which is the domain Map of the source graph. |
| rangeMap | [in] Range Map of the returned graph. If null, we use the default, which is the range Map of the source graph. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 2587 of file Tpetra_CrsGraph_decl.hpp.
| Teuchos::RCP< CrsGraphType > importAndFillCompleteCrsGraph | ( | const Teuchos::RCP< const CrsGraphType > & | sourceGraph, |
| const Import< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type > & | rowImporter, | ||
| const Import< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type > & | domainImporter, | ||
| const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> & | domainMap, | ||
| const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> & | rangeMap, | ||
| const Teuchos::RCP< Teuchos::ParameterList > & | params | ||
| ) |
Nonmember CrsGraph constructor that fuses Import and fillComplete().
| CrsGraphType | A specialization of CrsGraph. |
A common use case is to create an empty destination CrsGraph, redistribute from a source CrsGraph (by an Import or Export operation), then call fillComplete() on the destination CrsGraph. This constructor fuses these three cases, for an Import redistribution.
Fusing redistribution and fillComplete() exposes potential optimizations. For example, it may make constructing the column Map faster, and it may avoid intermediate unoptimized storage in the destination CrsGraph.
The resulting graph is fill complete (in the sense of isFillComplete()) and has optimized storage (in the sense of isStorageOptimized()). By default, its domain Map is the domain Map of the source graph, and its range Map is the range Map of the source graph.
| sourceGraph | [in] The source graph from which to import. The source of an Import must have a nonoverlapping distribution. |
| rowImporter | [in] The Import instance containing a precomputed redistribution plan. The source Map of the Import must be the same as the rowMap of sourceGraph unless the "Reverse Mode" option on the params list, in which case the targetMap of Import must match the rowMap of the sourceGraph |
| domainImporter | [in] The Import instance containing a precomputed redistribution plan. The source Map of the Import must be the same as the domainMap of sourceGraph unless the "Reverse Mode" option on the params list, in which case the targetMap of Import must match the domainMap of the sourceGraph |
| domainMap | [in] Domain Map of the returned graph. |
| rangeMap | [in] Range Map of the returned graph. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 2655 of file Tpetra_CrsGraph_decl.hpp.
| Teuchos::RCP< CrsGraphType > exportAndFillCompleteCrsGraph | ( | const Teuchos::RCP< const CrsGraphType > & | sourceGraph, |
| const Export< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type > & | exporter, | ||
| const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> & | domainMap = Teuchos::null, |
||
| const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> & | rangeMap = Teuchos::null, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Nonmember CrsGraph constructor that fuses Export and fillComplete().
| CrsGraphType | A specialization of CrsGraph. |
For justification, see the documentation of importAndFillCompleteCrsGraph() (which is the Import analog of this function).
The resulting graph is fill complete (in the sense of isFillComplete()) and has optimized storage (in the sense of isStorageOptimized()). By default, its domain Map is the domain Map of the source graph, and its range Map is the range Map of the source graph.
| sourceGraph | [in] The source graph from which to export. Its row Map may be overlapping, since the source of an Export may be overlapping. |
| exporter | [in] The Export instance containing a precomputed redistribution plan. The source Map of the Export must be the same as the row Map of sourceGraph. |
| domainMap | [in] Domain Map of the returned graph. If null, we use the default, which is the domain Map of the source graph. |
| rangeMap | [in] Range Map of the returned graph. If null, we use the default, which is the range Map of the source graph. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 2709 of file Tpetra_CrsGraph_decl.hpp.
| Teuchos::RCP< CrsGraphType > exportAndFillCompleteCrsGraph | ( | const Teuchos::RCP< const CrsGraphType > & | sourceGraph, |
| const Export< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type > & | rowExporter, | ||
| const Export< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type > & | domainExporter, | ||
| const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> & | domainMap, | ||
| const Teuchos::RCP< const Map< typename CrsGraphType::local_ordinal_type, typename CrsGraphType::global_ordinal_type, typename CrsGraphType::node_type >> & | rangeMap, | ||
| const Teuchos::RCP< Teuchos::ParameterList > & | params | ||
| ) |
Nonmember CrsGraph constructor that fuses Export and fillComplete().
| CrsGraphType | A specialization of CrsGraph. |
For justification, see the documentation of importAndFillCompleteCrsGraph() (which is the Import analog of this function).
The resulting graph is fill complete (in the sense of isFillComplete()) and has optimized storage (in the sense of isStorageOptimized()). By default, its domain Map is the domain Map of the source graph, and its range Map is the range Map of the source graph.
| sourceGraph | [in] The source graph from which to export. Its row Map may be overlapping, since the source of an Export may be overlapping. |
| rowExporter | [in] The Export instance containing a precomputed redistribution plan. The source Map of the Export must be the same as the row Map of sourceGraph. |
| domainExporter | [in] The Export instance containing a precomputed redistribution plan. The source Map of the Export must be the same as the domain Map of sourceGraph. |
| domainMap | [in] Domain Map of the returned graph. |
| rangeMap | [in] Range Map of the returned graph. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 2760 of file Tpetra_CrsGraph_decl.hpp.
| Teuchos::RCP< CrsMatrixType > Tpetra::importAndFillCompleteCrsMatrix | ( | const Teuchos::RCP< const CrsMatrixType > & | sourceMatrix, |
| const Import< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > & | importer, | ||
| const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > & | domainMap = Teuchos::null, |
||
| const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > & | rangeMap = Teuchos::null, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Nonmember CrsMatrix constructor that fuses Import and fillComplete().
| CrsMatrixType | A specialization of CrsMatrix. |
A common use case is to create an empty destination CrsMatrix, redistribute from a source CrsMatrix (by an Import or Export operation), then call fillComplete() on the destination CrsMatrix. This constructor fuses these three cases, for an Import redistribution.
Fusing redistribution and fillComplete() exposes potential optimizations. For example, it may make constructing the column Map faster, and it may avoid intermediate unoptimized storage in the destination CrsMatrix. These optimizations may improve performance for specialized kernels like sparse matrix-matrix multiply, as well as for redistributing data after doing load balancing.
The resulting matrix is fill complete (in the sense of isFillComplete()) and has optimized storage (in the sense of isStorageOptimized()). By default, its domain Map is the domain Map of the source matrix, and its range Map is the range Map of the source matrix.
| sourceMatrix | [in] The source matrix from which to import. The source of an Import must have a nonoverlapping distribution. |
| importer | [in] The Import instance containing a precomputed redistribution plan. The source Map of the Import must be the same as the rowMap of sourceMatrix unless the "Reverse Mode" option on the params list, in which case the targetMap of Import must match the rowMap of the sourceMatrix |
| domainMap | [in] Domain Map of the returned matrix. If null, we use the default, which is the domain Map of the source matrix. |
| rangeMap | [in] Range Map of the returned matrix. If null, we use the default, which is the range Map of the source matrix. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 4091 of file Tpetra_CrsMatrix_decl.hpp.
| Teuchos::RCP< CrsMatrixType > Tpetra::importAndFillCompleteCrsMatrix | ( | const Teuchos::RCP< const CrsMatrixType > & | sourceMatrix, |
| const Import< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > & | rowImporter, | ||
| const Import< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > & | domainImporter, | ||
| const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > & | domainMap, | ||
| const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > & | rangeMap, | ||
| const Teuchos::RCP< Teuchos::ParameterList > & | params | ||
| ) |
Nonmember CrsMatrix constructor that fuses Import and fillComplete().
| CrsMatrixType | A specialization of CrsMatrix. |
A common use case is to create an empty destination CrsMatrix, redistribute from a source CrsMatrix (by an Import or Export operation), then call fillComplete() on the destination CrsMatrix. This constructor fuses these three cases, for an Import redistribution.
Fusing redistribution and fillComplete() exposes potential optimizations. For example, it may make constructing the column Map faster, and it may avoid intermediate unoptimized storage in the destination CrsMatrix. These optimizations may improve performance for specialized kernels like sparse matrix-matrix multiply, as well as for redistributing data after doing load balancing.
The resulting matrix is fill complete (in the sense of isFillComplete()) and has optimized storage (in the sense of isStorageOptimized()). By default, its domain Map is the domain Map of the source matrix, and its range Map is the range Map of the source matrix.
| sourceMatrix | [in] The source matrix from which to import. The source of an Import must have a nonoverlapping distribution. |
| rowImporter | [in] The Import instance containing a precomputed redistribution plan. The source Map of the Import must be the same as the rowMap of sourceMatrix unless the "Reverse Mode" option on the params list, in which case the targetMap of Import must match the rowMap of the sourceMatrix |
| domainImporter | [in] The Import instance containing a precomputed redistribution plan. The source Map of the Import must be the same as the domainMap of sourceMatrix unless the "Reverse Mode" option on the params list, in which case the targetMap of Import must match the domainMap of the sourceMatrix |
| domainMap | [in] Domain Map of the returned matrix. |
| rangeMap | [in] Range Map of the returned matrix. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 4109 of file Tpetra_CrsMatrix_decl.hpp.
| Teuchos::RCP< CrsMatrixType > Tpetra::exportAndFillCompleteCrsMatrix | ( | const Teuchos::RCP< const CrsMatrixType > & | sourceMatrix, |
| const Export< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > & | exporter, | ||
| const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > & | domainMap = Teuchos::null, |
||
| const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > & | rangeMap = Teuchos::null, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Nonmember CrsMatrix constructor that fuses Export and fillComplete().
| CrsMatrixType | A specialization of CrsMatrix. |
For justification, see the documentation of importAndFillCompleteCrsMatrix() (which is the Import analog of this function).
The resulting matrix is fill complete (in the sense of isFillComplete()) and has optimized storage (in the sense of isStorageOptimized()). By default, its domain Map is the domain Map of the source matrix, and its range Map is the range Map of the source matrix.
| sourceMatrix | [in] The source matrix from which to export. Its row Map may be overlapping, since the source of an Export may be overlapping. |
| exporter | [in] The Export instance containing a precomputed redistribution plan. The source Map of the Export must be the same as the row Map of sourceMatrix. |
| domainMap | [in] Domain Map of the returned matrix. If null, we use the default, which is the domain Map of the source matrix. |
| rangeMap | [in] Range Map of the returned matrix. If null, we use the default, which is the range Map of the source matrix. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 4130 of file Tpetra_CrsMatrix_decl.hpp.
| Teuchos::RCP< CrsMatrixType > Tpetra::exportAndFillCompleteCrsMatrix | ( | const Teuchos::RCP< const CrsMatrixType > & | sourceMatrix, |
| const Export< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > & | rowExporter, | ||
| const Export< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > & | domainExporter, | ||
| const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > & | domainMap, | ||
| const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > & | rangeMap, | ||
| const Teuchos::RCP< Teuchos::ParameterList > & | params | ||
| ) |
Nonmember CrsMatrix constructor that fuses Export and fillComplete().
| CrsMatrixType | A specialization of CrsMatrix. |
For justification, see the documentation of importAndFillCompleteCrsMatrix() (which is the Import analog of this function).
The resulting matrix is fill complete (in the sense of isFillComplete()) and has optimized storage (in the sense of isStorageOptimized()). By default, its domain Map is the domain Map of the source matrix, and its range Map is the range Map of the source matrix.
| sourceMatrix | [in] The source matrix from which to export. Its row Map may be overlapping, since the source of an Export may be overlapping. |
| rowExporter | [in] The Export instance containing a precomputed redistribution plan. The source Map of the Export must be the same as the row Map of sourceMatrix. |
| domainExporter | [in] The Export instance containing a precomputed redistribution plan. The source Map of the Export must be the same as the domain Map of sourceMatrix. |
| domainMap | [in] Domain Map of the returned matrix. |
| rangeMap | [in] Range Map of the returned matrix. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 4148 of file Tpetra_CrsMatrix_decl.hpp.
| Teuchos::RCP< CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node > > createCrsMatrix | ( | const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > & | map, |
| const size_t | maxNumEntriesPerRow = 0, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Create an empty CrsMatrix given a row map and a single integer upper bound on the number of stored entries per row.
Definition at line 4079 of file Tpetra_CrsMatrix_decl.hpp.
| void removeCrsMatrixZeros | ( | CrsMatrixType & | matrix, |
| typename Teuchos::ScalarTraits< typename CrsMatrixType::scalar_type >::magnitudeType const & | threshold = Teuchos::ScalarTraits<typename CrsMatrixType::scalar_type>::magnitude(Teuchos::ScalarTraits<typename CrsMatrixType::scalar_type>::zero()) |
||
| ) |
Remove zero entries from a matrix.
| matrix | [in/out] CrsMatrix |
| threshold | [in] magnitude threshold below which an entry is deemed to be zero |
Definition at line 4174 of file Tpetra_CrsMatrix_decl.hpp.
| Teuchos::RCP< CrsMatrixMultiplyOp< OpScalar, MatScalar, LocalOrdinal, GlobalOrdinal, Node > > createCrsMatrixMultiplyOp | ( | const Teuchos::RCP< const CrsMatrix< MatScalar, LocalOrdinal, GlobalOrdinal, Node > > & | A | ) |
Non-member function to create a CrsMatrixMultiplyOp.
The function has the same template parameters of CrsMatrixMultiplyOp.
| A | [in] The CrsMatrix instance to wrap in an CrsMatrixMultiplyOp. |
Definition at line 602 of file Tpetra_CrsMatrixMultiplyOp.hpp.
| void Tpetra::removeEmptyProcessesInPlace | ( | Teuchos::RCP< DistObjectType > & | input, |
| const Teuchos::RCP< const Map< typename DistObjectType::local_ordinal_type, typename DistObjectType::global_ordinal_type, typename DistObjectType::node_type > > & | newMap | ||
| ) |
Remove processes which contain no elements in this object's Map.
| DistObjectType | A specialization of DistObject. |
Vocabulary:
input->getMap() on input to this method is the "original Map."The communicator returned by input->getComm() on input to this method is the "original communicator."All processes in the original communicator which contain zero elements in the original Map are "excluded processes."All other processes in the original communicator are "included
processes."Preconditions:
input is distributed over the original Map.newMap must be the same as the result of calling removeEmptyProcesses() on the original Map.newMap must be Teuchos::null. (This is what getMap()->removeEmptyProcesses() returns anyway on excluded processes.)This method has collective semantics over the original communicator. On included processes, reassign this object's Map (that would be returned by getMap()) to the input newMap, and do any work that needs to be done to restore correct semantics. The input DistObject input will be nonnull on return. On excluded processes, free any data in input that need freeing, do any other work that needs to be done to restore correct semantics, and set input to null before returning.
The two-argument version of this function is useful if you have already precomputed the new Map that excludes processes with zero elements. For example, you might want to apply this Map to several different MultiVector instances. The one-argument version of this function is useful if you want the DistObject to compute the new Map itself, because you only plan to use it for that one DistObject instance.
Here is a sample use case. Suppose that input is some subclass of DistObject, like MultiVector, CrsGraph, or CrsMatrix. Suppose also that map_type is the corresponding specialization of Map.
input. Calling any methods (other than the destructor) on the input on excluded processes has undefined behavior in that case, and may result in deadlock.| void Tpetra::removeEmptyProcessesInPlace | ( | Teuchos::RCP< DistObjectType > & | input | ) |
Remove processes which contain no elements in this object's Map.
| DistObjectType | A specialization of DistObject. |
This method behaves just like the two-argument version of removeEmptyProcessesInPlace(), except that it first calls removeEmptyProcesses() on the input DistObject's Map to compute the new Map.
The two-argument version of this function is useful if you have already precomputed the new Map that excludes processes with zero elements. For example, you might want to apply this Map to several different MultiVector instances. The one-argument version of this function is useful if you want the DistObject to compute the new Map itself, because you only plan to use it for that one DistObject instance.
Here is a sample use case. Suppose that input is some subclass of DistObject, like MultiVector, CrsGraph, or CrsMatrix. Suppose also that map_type is the corresponding specialization of Map.
Definition at line 1864 of file Tpetra_DistObject_def.hpp.
| Teuchos::RCP< const Export< LocalOrdinal, GlobalOrdinal, Node > > createExport | ( | const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > & | src, |
| const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > & | tgt | ||
| ) |
Nonmember "constructor" for Export objects.
Create an Export object from the given source and target Maps.
src != null tgt != nullsrc == tgt, returns null.(Debug mode: throws std::runtime_error if one of src or tgt is null.)
Definition at line 253 of file Tpetra_Export_decl.hpp.
| Teuchos::RCP<matrix_type> Tpetra::applyFilter_vals | ( | const matrix_type & | A, |
| const filter_type & | filter | ||
| ) |
Constructs a matrix consisting only of the entries for which the filter function evaluates to true.
This applies a filter function that takes as single argument the value of the matrix entry.
| A | [in] The source matrix that the filter will be applied to. |
| filter | [in] A callable with signature (impl_scalar_type, ) -> bool. |
Definition at line 17 of file Tpetra_Filter.hpp.
| Teuchos::RCP<matrix_type> Tpetra::applyFilter_LID | ( | const matrix_type & | A, |
| const filter_type & | filter | ||
| ) |
Constructs a matrix consisting only of the entries for which the filter function evaluates to true.
This applies a filter function that takes as arguments the local row and column ids and the value of the matrix entry.
| A | [in] The source matrix that the filter will be applied to. |
| filter | [in] A callable with signature (local_ordinal_type, local_ordinal_type, impl_scalar_type) -> bool. |
Definition at line 79 of file Tpetra_Filter.hpp.
| Teuchos::RCP<matrix_type> Tpetra::applyFilter_GID | ( | const matrix_type & | A, |
| const filter_type & | filter | ||
| ) |
Constructs a matrix consisting only of the entries for which the filter function evaluates to true.
This applies a filter function that takes as arguments the global row and column ids and the value of the matrix entry.
| A | [in] The source matrix that the filter will be applied to. |
| filter | [in] A callable with signature (global_ordinal_type, global_ordinal_type, impl_scalar_type) -> bool. |
Definition at line 142 of file Tpetra_Filter.hpp.
| std::shared_ptr<::Tpetra::Details::CommRequest> Tpetra::idot | ( | typename::Tpetra::MultiVector< SC, LO, GO, NT >::dot_type * | resultRaw, |
| const ::Tpetra::MultiVector< SC, LO, GO, NT > & | X, | ||
| const ::Tpetra::MultiVector< SC, LO, GO, NT > & | Y | ||
| ) |
Nonblocking dot product, with either Tpetra::MultiVector or Tpetra::Vector inputs, and raw pointer or raw array output.
This implements the following cases:
| resultRaw | [out] Output; raw pointer or raw array to the return value(s). It is only valid to read this after calling wait() on the return value. It must be legal to write to the first std::max(X.getNumVectors(), Y.getNumVectors()) entries of this array. This memory must be accessible from the host CPU. |
| X | [in] First input Tpetra::MultiVector or Tpetra::Vector. This must have same number of rows (globally, and on each (MPI) process) as Y. If this is a Tpetra::MultiVector, then this must either have the same number of columns as Y, or have one column. |
| Y | [in] Second input Tpetra::MultiVector or Tpetra::Vector. This must have same number of rows (globally, and on each (MPI) process) as X. If this is a Tpetra::MultiVector, then this must either have the same number of columns as X, or have one column. |
| SC | Same as the first template parameter of Tpetra::Vector. |
| LO | Same as the second template parameter of Tpetra::Vector. |
| GO | Same as the third template parameter of Tpetra::Vector. |
| NT | Same as the fourth template parameter of Tpetra::Vector. |
In this version of the function, the dot product result goes into an array (just a raw pointer). The dot_type typedef is the type of a dot product result, for a Tpetra::Vector whose entries have type SC (the "Scalar" type). For most SC types, dot_type == SC. However, once you start dipping into more interesting Scalar types, such as those found in the Sacado or Stokhos packages, dot_type may be a different type. Most users should not have to worry about this, but Tpetra developers may need to worry about this.
Definition at line 241 of file Tpetra_idot.hpp.
| std::shared_ptr<::Tpetra::Details::CommRequest> Tpetra::idot | ( | const Kokkos::View< typename::Tpetra::MultiVector< SC, LO, GO, NT >::dot_type *, typename::Tpetra::MultiVector< SC, LO, GO, NT >::device_type > & | result, |
| const ::Tpetra::MultiVector< SC, LO, GO, NT > & | X, | ||
| const ::Tpetra::MultiVector< SC, LO, GO, NT > & | Y | ||
| ) |
Nonblocking dot product, with Tpetra::MultiVector inputs, and rank-1 (one-dimensional array) Kokkos::View output.
This implements the following cases:
| result | [out] Output; rank-1 Kokkos::View. It is only valid to read the entries of this after calling wait() on the return value. This must have length std::max(X.getNumVectors(), Y.getNumVectors()). |
| X | [in] First input Tpetra::MultiVector or Tpetra::Vector. This must have same number of rows (globally, and on each (MPI) process) as Y. If this is a Tpetra::MultiVector, then this must either have the same number of columns as Y, or have one column. |
| Y | [in] Second input Tpetra::MultiVector or Tpetra::Vector. This must have same number of rows (globally, and on each (MPI) process) as X. If this is a Tpetra::MultiVector, then this must either have the same number of columns as X, or have one column. |
| SC | Same as the first template parameter of Tpetra::MultiVector. |
| LO | Same as the second template parameter of Tpetra::MultiVector. |
| GO | Same as the third template parameter of Tpetra::MultiVector. |
| NT | Same as the fourth template parameter of Tpetra::MultiVector. |
Compute the dot product of each column of X, with each corresponding column of Y. If X has a single column, then compute the dot product of X with each column of Y in turn. If Y has a single column, then compute the dot product of each column of X in turn with Y.
In this version of the function, the dot product results go into a rank-1 (one-dimensional) Kokkos::View. We prefer that you use the versions of idot() that take a Kokkos::View as their output argument, because this ensures that the output will still exist (not be deallocated or fall out of scope). The versions of idot() that take a raw pointer cannot promise that the memory will continue to exist until the dot product is done.
The dot_type typedef is the type of a dot product result, for a Tpetra::Vector whose entries have type SC (the "Scalar" type). For most SC types, dot_type == SC. However, once you start dipping into more interesting Scalar types, such as those found in the Sacado or Stokhos packages, dot_type may be a different type. Most users should not have to worry about this, but Tpetra developers may need to worry about this.
Definition at line 317 of file Tpetra_idot.hpp.
| std::shared_ptr<::Tpetra::Details::CommRequest> Tpetra::idot | ( | const Kokkos::View< typename::Tpetra::Vector< SC, LO, GO, NT >::dot_type, typename::Tpetra::Vector< SC, LO, GO, NT >::device_type > & | result, |
| const ::Tpetra::Vector< SC, LO, GO, NT > & | X, | ||
| const ::Tpetra::Vector< SC, LO, GO, NT > & | Y | ||
| ) |
Nonblocking dot product, with Tpetra::Vector inputs, and rank-0 (single value) Kokkos::View output.
This function computes result() = dot(X,Y).
| result | [out] Output; rank-0 Kokkos::View of the return value. It is only valid to read this after calling wait() on the return value. |
| X | [in] First input Tpetra::Vector. This must have same number of rows (globally, and on each (MPI) process) as Y. |
| Y | [in] Second input Tpetra::Vector. This must have same number of rows (globally, and on each (MPI) process) as X. |
| SC | Same as the first template parameter of Tpetra::Vector. |
| LO | Same as the second template parameter of Tpetra::Vector. |
| GO | Same as the third template parameter of Tpetra::Vector. |
| NT | Same as the fourth template parameter of Tpetra::Vector. |
In this version of the function, the dot product result goes into a rank-0 ("zero-dimensional") Kokkos::View. Rank-0 Views just view a single value. We prefer that you use the versions of idot() that take a Kokkos::View as their output argument, because this ensures that the output will still exist (not be deallocated or fall out of scope). The versions of idot() that take a raw pointer cannot promise that the memory will continue to exist until the dot product is done.
The dot_type typedef is the type of a dot product result, for a Tpetra::Vector whose entries have type SC (the "Scalar" type). For most SC types, dot_type == SC. However, once you start dipping into more interesting Scalar types, such as those found in the Sacado or Stokhos packages, dot_type may be a different type. Most users should not have to worry about this, but Tpetra developers may need to worry about this.
Definition at line 367 of file Tpetra_idot.hpp.
| Teuchos::RCP< const Import< LocalOrdinal, GlobalOrdinal, Node > > createImport | ( | const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> & | src, |
| const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> & | tgt | ||
| ) |
Nonmember constructor for Import.
Create a Import object from the given source and target Maps.
src != null tgt != null src == tgt, returns null. (Debug mode: throws std::runtime_error if one of src or tgt is null.) Definition at line 498 of file Tpetra_Import_decl.hpp.
| Teuchos::RCP< const Import< LocalOrdinal, GlobalOrdinal, Node > > createImport | ( | const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> & | src, |
| const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> & | tgt, | ||
| const Teuchos::RCP< Teuchos::ParameterList > & | plist | ||
| ) |
Nonmember constructor for Import that takes a ParameterList.
Create a Import object from the given source and target Maps, using the given list of parameters.
src != null tgt != null src == tgt, returns null. (Debug mode: throws std::runtime_error if one of src or tgt is null.) Definition at line 524 of file Tpetra_Import_decl.hpp.
| void Tpetra::leftAndOrRightScaleCrsMatrix | ( | Tpetra::CrsMatrix< SC, LO, GO, NT > & | A, |
| const Kokkos::View< const typename Kokkos::ArithTraits< SC >::mag_type *, typename NT::device_type > & | rowScalingFactors, | ||
| const Kokkos::View< const typename Kokkos::ArithTraits< SC >::mag_type *, typename NT::device_type > & | colScalingFactors, | ||
| const bool | leftScale, | ||
| const bool | rightScale, | ||
| const bool | assumeSymmetric, | ||
| const EScaling | scaling | ||
| ) |
Left-scale and/or right-scale (in that order) the entries of the input Tpetra::CrsMatrix A.
| A | [in/out] The sparse matrix A to scale. It must have a valid KokkosSparse::CrsMatrix. This is true if fillComplete has been called on it at least once, or if the matrix was created with a local sparse matrix. |
| rowScalingFactors | [in] Use Details::EquilibrationInfo::rowNorms. |
| colScalingFactors | [in] If assumeSymmetric, use Details::EquilibrationInfo::colNorms, else use Details::EquilibrationInfo::rowScaledColNorms. |
| leftScale | [in] Whether to left-scale A. Left scaling happens first. |
| rightScale | [in] Whether to right-scale A. Right scaling happens last. |
| Whether | to assume symmetric scaling, that is, whether to take square roots of scaling factors before scaling. |
| scaling | [in] If SCALING_DIVIDE, "scale" means "divide by"; if SCALING_MULTIPLY, it means "multiply by." |
Definition at line 30 of file Tpetra_leftAndOrRightScaleCrsMatrix_def.hpp.
| void Tpetra::leftAndOrRightScaleCrsMatrix | ( | Tpetra::CrsMatrix< SC, LO, GO, NT > & | A, |
| const Tpetra::Vector< typename Kokkos::ArithTraits< SC >::mag_type, LO, GO, NT > & | rowScalingFactors, | ||
| const Tpetra::Vector< typename Kokkos::ArithTraits< SC >::mag_type, LO, GO, NT > & | colScalingFactors, | ||
| const bool | leftScale, | ||
| const bool | rightScale, | ||
| const bool | assumeSymmetric, | ||
| const EScaling | scaling | ||
| ) |
Left-scale and/or right-scale (in that order) the entries of the input Tpetra::CrsMatrix A.
| A | [in/out] The sparse matrix A to scale. It must have a valid KokkosSparse::CrsMatrix. This is true if fillComplete has been called on it at least once, or if the matrix was created with a local sparse matrix. |
| rowScalingFactors | [in] The row scaling factors; must be distributed according to the matrix's row Map. This function does NOT redistribute the Vector for you. |
| colScalingFactors | [in] The column scaling factors; must be distributed according to the matrix's column Map. This function does NOT redistribute the Vector for you. |
| leftScale | [in] Whether to left-scale A. Left scaling happens first. |
| rightScale | [in] Whether to right-scale A. Right scaling happens last. |
| Whether | to assume symmetric scaling, that is, whether to take square roots of scaling factors before scaling. |
| scaling | [in] If SCALING_DIVIDE, "scale" means "divide by"; if SCALING_MULTIPLY, it means "multiply by." |
Definition at line 95 of file Tpetra_leftAndOrRightScaleCrsMatrix_def.hpp.
| Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal > > createLocalMap | ( | const size_t | numElements, |
| const Teuchos::RCP< const Teuchos::Comm< int >> & | comm | ||
| ) |
Nonmember constructor for a locally replicated Map with the default Kokkos Node.
This method returns a Map instantiated on the default Kokkos Node type. The Map is configured to use zero-based indexing.
| numElements | [in] Number of elements on each process. Each process gets the same set of elements, namely 0, 1, ..., numElements - 1. |
| comm | [in] The Map's communicator. |
| Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > createLocalMapWithNode | ( | const size_t | numElements, |
| const Teuchos::RCP< const Teuchos::Comm< int >> & | comm | ||
| ) |
Nonmember constructor for a locally replicated Map with a specified Kokkos Node.
This method returns a Map instantiated on the given Kokkos Node instance. The Map is configured to use zero-based indexing.
| numElements | [in] Number of elements on each process. Each process gets the same set of elements, namely 0, 1, ..., numElements - 1. |
| comm | [in] The Map's communicator. |
| Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal > > createUniformContigMap | ( | const global_size_t | numElements, |
| const Teuchos::RCP< const Teuchos::Comm< int >> & | comm | ||
| ) |
| Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > createUniformContigMapWithNode | ( | const global_size_t | numElements, |
| const Teuchos::RCP< const Teuchos::Comm< int >> & | comm | ||
| ) |
| Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal > > createContigMap | ( | const global_size_t | numElements, |
| const size_t | localNumElements, | ||
| const Teuchos::RCP< const Teuchos::Comm< int >> & | comm | ||
| ) |
| Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > createContigMapWithNode | ( | const global_size_t | numElements, |
| const size_t | localNumElements, | ||
| const Teuchos::RCP< const Teuchos::Comm< int >> & | comm | ||
| ) |
| Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal > > createNonContigMap | ( | const Teuchos::ArrayView< const GlobalOrdinal > & | elementList, |
| const Teuchos::RCP< const Teuchos::Comm< int >> & | comm | ||
| ) |
| Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > createNonContigMapWithNode | ( | const Teuchos::ArrayView< const GlobalOrdinal > & | elementList, |
| const Teuchos::RCP< const Teuchos::Comm< int >> & | comm | ||
| ) |
| Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > createOneToOne | ( | const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> & | M | ) |
| Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > createOneToOne | ( | const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> & | M, |
| const ::Tpetra::Details::TieBreak< LocalOrdinal, GlobalOrdinal > & | tie_break | ||
| ) |
Creates a one-to-one version of the given Map where each GID lives on only one process. The given TieBreak object specifies the rule to break ties.
| Teuchos::RCP< MixedScalarMultiplyOp< Scalar, OpScalar, LocalOrdinal, GlobalOrdinal, Node > > createMixedScalarMultiplyOp | ( | const Teuchos::RCP< const Operator< OpScalar, LocalOrdinal, GlobalOrdinal, Node > > & | A | ) |
Non-member function to create a MixedScalarMultiplyOp.
The function has the same template parameters of MixedScalarMultiplyOp.
| A | [in] The Operator instance to wrap in an MixedScalarMultiplyOp. |
Definition at line 141 of file Tpetra_MixedScalarMultiplyOp.hpp.
| void Tpetra::deep_copy | ( | MultiVector< DS, DL, DG, DN > & | dst, |
| const MultiVector< SS, SL, SG, SN > & | src | ||
| ) |
Copy the contents of the MultiVector src into dst.
src must be compatible with the Map of dst. Copy the contents of the MultiVector src into the MultiVector dst. ("Copy the contents" means the same thing as "deep
copy.") The two MultiVectors need not necessarily have the same template parameters, but the assignment of their entries must make sense. Furthermore, their Maps must be compatible, that is, the MultiVectors' local dimensions must be the same on all processes.
This method must always be called as a collective operation on all processes over which the multivector is distributed. This is because the method reserves the right to check for compatibility of the two Maps, at least in debug mode, and throw if they are not compatible.
Definition at line 2420 of file Tpetra_MultiVector_decl.hpp.
| MultiVector< ST, LO, GO, NT > Tpetra::createCopy | ( | const MultiVector< ST, LO, GO, NT > & | src | ) |
Return a deep copy of the given MultiVector.
Definition at line 4653 of file Tpetra_MultiVector_def.hpp.
| Teuchos::RCP< MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > createMultiVector | ( | const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node >> & | map, |
| const size_t | numVectors | ||
| ) |
Nonmember MultiVector "constructor": Create a MultiVector from a given Map.
| map | [in] Map describing the distribution of rows of the resulting MultiVector. |
| numVectors | [in] Number of columns of the resulting MultiVector. |
| void Tpetra::deep_copy | ( | MultiVector< ST, LO, GO, NT > & | dst, |
| const MultiVector< ST, LO, GO, NT > & | src | ||
| ) |
Specialization of deep_copy for MultiVector objects with the same template parameters.
Definition at line 2409 of file Tpetra_MultiVector_decl.hpp.
| LO Tpetra::replaceDiagonalCrsMatrix | ( | ::Tpetra::CrsMatrix< SC, LO, GO, NT > & | matrix, |
| const ::Tpetra::Vector< SC, LO, GO, NT > & | newDiag | ||
| ) |
Replace diagonal entries of an input Tpetra::CrsMatrix matrix with values given in newDiag.
| Scalar | The type of the numerical entries of the matrix. (You can use real-valued or complex-valued types here, unlike in Epetra, where the scalar type is always double.) |
| LocalOrdinal | The type of local indices. See the documentation of Map for requirements. |
| GlobalOrdinal | The type of global indices. See the documentation of Map for requirements. |
| Node | The Kokkos Node type. See the documentation of Map for requirements. |
| in/out] | matrix Tpetra::CrsMatrix to be modified | |
| [in] | newDiag | Tpetra::Vector with new values for the diagonal; must have same Tpetra::Map as matrix's rowMap |
| MapType::iterator Tpetra::efficientAddOrUpdate | ( | MapType & | m, |
| const KeyArgType & | k, | ||
| const ValueArgType & | v | ||
| ) |
Efficiently insert or replace an entry in an std::map.
| MapType | Specialization of std::map |
| KeyArgType | Type of keys of the std::map |
| ValueArgType | Type of values of the std::map |
This function is taken from Scott Meyers' "Effective STL", Item
Definition at line 175 of file Tpetra_Util.hpp.
| void Tpetra::sort2 | ( | const IT1 & | first1, |
| const IT1 & | last1, | ||
| const IT2 & | first2, | ||
| const bool | stableSort = false |
||
| ) |
Sort the first array, and apply the resulting permutation to the second array.
Sort the values in the first array (represented by the exclusive iterator range first1,last1) in ascending order. Apply the permutation resulting from the sort to the second array (represented by a starting iterator first2).
| first1 | A random access iterator pointing to the beginning of the first array. |
| last1 | A random access iterator pointing to the end (exclusive) of the first array. |
| first2 | A random access iterator pointing to the beginning of the second array. The second array must have no fewer elements than the first array. If the first array has N elements, then the permutation will only be applied to the first N elements of the second array. |
Definition at line 539 of file Tpetra_Util.hpp.
| void Tpetra::sort2 | ( | View1 & | view1, |
| const size_t & | size, | ||
| View2 & | view2 | ||
| ) |
Sort the first array, and apply the resulting permutation to the second array.
Sort the values in the first array (of length size) in ascending order. Apply the permutation resulting from the sort to the second array
| view1 | A host-accessible 1D Kokkos::View of the first array. |
| size | Length of the first array. |
| view2 | A host-accessible 1D Kokkos::View of the second array. The second array must have no fewer elements than the first array. If the first array has N elements, then the permutation will only be applied to the first N elements of the second array. |
Definition at line 576 of file Tpetra_Util.hpp.
| void Tpetra::sort | ( | View & | view, |
| const size_t & | size | ||
| ) |
Convenience wrapper for std::sort for host-accessible views.
Sort the values in the array (of length size) in ascending order.
| view | A host-accessible 1D Kokkos::View. |
| size | Length of the first array (or portion of which to sort). |
Definition at line 595 of file Tpetra_Util.hpp.
| void Tpetra::reverse_sort | ( | View & | view, |
| const size_t & | size | ||
| ) |
Convenience wrapper for a reversed std::sort for host-accessible views.
Reverse Sort the values in the array (of length size) in ascending order.
| view | A host-accessible 1D Kokkos::View. |
| size | Length of the array (or portion of which to sort, from the end) |
Definition at line 613 of file Tpetra_Util.hpp.
| void Tpetra::sort3 | ( | const IT1 & | first1, |
| const IT1 & | last1, | ||
| const IT2 & | first2, | ||
| const IT3 & | first3, | ||
| const bool | stableSort = false |
||
| ) |
Sort the first array, and apply the same permutation to the second and third arrays.
Sort the values in the first array (represented by the exclusive iterator range first1,last1) in ascending order. Apply the permutation resulting from the sort to the second array (represented by a starting iterator first2) and third array (represented by a starting iterator first3).
| first1 | A random access iterator pointing to the beginning of the first array. |
| last1 | A random access iterator pointing to the end (exclusive) of the first array. |
| first2 | A random access iterator pointing to the beginning of the second array. |
| first3 | A random access iterator pointing to the beginning of the third array. |
Definition at line 637 of file Tpetra_Util.hpp.
| void Tpetra::merge2 | ( | IT1 & | indResultOut, |
| IT2 & | valResultOut, | ||
| IT1 | indBeg, | ||
| IT1 | indEnd, | ||
| IT2 | valBeg, | ||
| IT2 | |||
| ) |
Merge values in place, additively, with the same index.
| IT1 | Iterator type for the range of indices |
| IT2 | Iterator type for the range of values |
indBeg, indEnd defines a half-exclusive (does not include the end) range of indices, and valBeg, valEnd its corresponding range of values. The range of values must have the same number of entries as the range of indices. In every nondecreasing subsequence of indices, this method will merge values that have the same index, by adding the values together. When done, it assigns the new end (exclusive) of the index range to indResultOut, and the new end (exclusive) of the value range to valResultOut. (It is legal for the index range not to be sorted, but then only nondecreasing subsequences will get merged.)
For example, if the indices on input are {0, 1, 1, 3, -1, -1, -1, 0}, and their corresponding values on input are {42.0, -4.0, -3.0, 1.5, 1.0, 2.0, 3.0}, then on exit from this function, the indices are {0, 1, 3, -1, 0}, and the values are {42.0, -7.0, 1.5, 6.0, 100.0}.
On entry to the function, indResultOut may alias indEnd, and valResultOut may alias valEnd. For example, the following code is legal:
However, the following code is not legal, because the return value of std::vector::end() cannot be modified:
Definition at line 704 of file Tpetra_Util.hpp.
| void Tpetra::merge2 | ( | IT1 & | indResultOut, |
| IT2 & | valResultOut, | ||
| IT1 | indBeg, | ||
| IT1 | indEnd, | ||
| IT2 | valBeg, | ||
| IT2 | valEnd, | ||
| BinaryFunction | f | ||
| ) |
Merge values in place with the same index, using any associative binary function.
| IT1 | Iterator type for the range of indices |
| IT2 | Iterator type for the range of values |
| BinaryFunction | The type of a function that takes two values and returns another value. |
indBeg, indEnd defines a half-exclusive (does not include the end) range of indices, and valBeg, valEnd its corresponding range of values. The range of values must have the same number of entries as the range of indices. In every nondecreasing subsequence of indices, this method will merge values that have the same index, by using the given binary function. When done, it assigns the new end (exclusive) of the index range to indResultOut, and the new end (exclusive) of the value range to valResultOut. (It is legal for the index range not to be sorted, but then only nondecreasing subsequences will get merged.)
For example, if the indices on input are {0, 1, 1, 3, -1, -1, -1, 0}, their corresponding values on input are {42.0, -4.0, -3.0, 1.5, 1.0, 2.0, 3.0}, and the binary function is an instance of std::plus<double>, then on exit from this function, the indices are {0, 1, 3, -1, 0}, and the values are {42.0, -7.0, 1.5, 6.0, 100.0}.
On entry to the function, indResultOut may alias indEnd, and valResultOut may alias valEnd. For example, the following code is legal:
However, the following code is not legal, because the return value of std::vector::end() cannot be modified:
Definition at line 790 of file Tpetra_Util.hpp.
| void Tpetra::keyValueMerge | ( | KeyInputIterType | keyBeg1, |
| KeyInputIterType | keyEnd1, | ||
| ValueInputIterType | valBeg1, | ||
| ValueInputIterType | valEnd1, | ||
| KeyInputIterType | keyBeg2, | ||
| KeyInputIterType | keyEnd2, | ||
| ValueInputIterType | valBeg2, | ||
| ValueInputIterType | valEnd2, | ||
| KeyOutputIterType | keyOut, | ||
| ValueOutputIterType | valOut, | ||
| BinaryFunction | f | ||
| ) |
Merge two sorted (by keys) sequences of unique (key,value) pairs by combining pairs with equal keys.
| keyBeg1 | [in] Start of first sequence of keys. |
| keyEnd1 | [in] End (exclusive) of first sequence of keys. |
| valBeg1 | [in] Start of first sequence of values. |
| valEnd1 | [in] End (exclusive) of first sequence of values. |
| keyBeg2 | [in] Start of second sequence of keys. |
| keyEnd2 | [in] End (exclusive) of second sequence of keys. |
| valBeg2 | [in] Start of second sequence of values. |
| valEnd2 | [in] End (exclusive) of second sequence of values. |
| keyOut | [in/out] Output sequence of keys. |
| valOut | [in/out] Output sequence of values. |
| f | [in] Binary associative function to use to combine values whose keys are equal. For example, for simple replacement, use a function like std::project1st (in the SGI extensions to the STL) with both template parameters equal to the value type. For addition, use std::plus with template parameter equal to the value type. |
Definition at line 854 of file Tpetra_Util.hpp.
| Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > Tpetra::createCopy | ( | const Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | src | ) |
Return a deep copy of the given Vector.
Definition at line 211 of file Tpetra_Vector_def.hpp.
| Teuchos::RCP< Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > createVector | ( | const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > & | map | ) |
 1.8.5
1.8.5