|
Tpetra Matrix/Vector Services
Version of the Day
|
All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Groups Pages
|
Tpetra Matrix/Vector Services
Version of the Day
|
Partial specialization of CrsMatrix for the new Kokkos wrapper Nodes. More...
#include <Tpetra_KokkosRefactor_CrsMatrix_decl.hpp>
Public Types | |
Typedefs | |
| typedef Scalar | scalar_type |
| This class' first template parameter; the type of entries in the matrix. More... | |
| typedef LocalOrdinal | local_ordinal_type |
| This class' second template parameter; the type of local indices. More... | |
| typedef GlobalOrdinal | global_ordinal_type |
| This class' third template parameter; the type of global indices. More... | |
| typedef DeviceType | device_type |
| This class' fourth template parameter; the Kokkos device type. More... | |
| typedef Kokkos::Compat::KokkosDeviceWrapperNode < DeviceType > | node_type |
| The Kokkos Node type used by this class. More... | |
| typedef Map< LocalOrdinal, GlobalOrdinal, node_type > | map_type |
| The Map specialization suitable for this CrsMatrix specialization. More... | |
| typedef Import< LocalOrdinal, GlobalOrdinal, node_type > | import_type |
| The Import specialization suitable for this CrsMatrix specialization. More... | |
| typedef Export< LocalOrdinal, GlobalOrdinal, node_type > | export_type |
| The Export specialization suitable for this CrsMatrix specialization. More... | |
| typedef CrsGraph< LocalOrdinal, GlobalOrdinal, node_type > | crs_graph_type |
| The CrsGraph specialization suitable for this CrsMatrix specialization. More... | |
| typedef crs_graph_type::t_RowPtrs | t_RowPtrs |
|
typedef crs_graph_type::t_LocalOrdinal_1D | t_LocalOrdinal_1D |
|
typedef Kokkos::View< Scalar *, device_type > | t_ValuesType |
|
typedef Kokkos::CrsMatrix < Scalar, LocalOrdinal, device_type, void, size_t > | k_local_matrix_type |
Typedefs | |
| typedef char | packet_type |
| The type of each datum being sent or received in an Import or Export. More... | |
Public Member Functions | |
| t_ValuesType | getLocalValuesView () const |
| Get the Kokkos local values. More... | |
| void | importAndFillComplete (Teuchos::RCP< CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, node_type > > &destMatrix, const import_type &importer, const Teuchos::RCP< const map_type > &domainMap, const Teuchos::RCP< const map_type > &rangeMap, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) const |
Import from this to the given destination matrix, and make the result fill complete. More... | |
| void | exportAndFillComplete (Teuchos::RCP< CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, node_type > > &destMatrix, const export_type &exporter, const Teuchos::RCP< const map_type > &domainMap=Teuchos::null, const Teuchos::RCP< const map_type > &rangeMap=Teuchos::null, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) const |
Export from this to the given destination matrix, and make the result fill complete. More... | |
Methods for inserting, modifying, or removing entries | |
| void | insertGlobalValues (const GlobalOrdinal globalRow, const ArrayView< const GlobalOrdinal > &cols, const ArrayView< const Scalar > &vals) |
| Insert one or more entries into the matrix, using global indices. More... | |
| void | insertLocalValues (const LocalOrdinal localRow, const ArrayView< const LocalOrdinal > &cols, const ArrayView< const Scalar > &vals) |
| Insert one or more entries into the matrix, using local indices. More... | |
| LocalOrdinal | replaceGlobalValues (GlobalOrdinal globalRow, const ArrayView< const GlobalOrdinal > &cols, const ArrayView< const Scalar > &vals) |
| Replace one or more entries' values, using global indices. More... | |
| LocalOrdinal | replaceLocalValues (const LocalOrdinal localRow, const ArrayView< const LocalOrdinal > &cols, const ArrayView< const Scalar > &vals) |
| Replace one or more entries' values, using local indices. More... | |
| LocalOrdinal | sumIntoGlobalValues (const GlobalOrdinal globalRow, const ArrayView< const GlobalOrdinal > &cols, const ArrayView< const Scalar > &vals) |
| Sum into one or more sparse matrix entries, using global indices. More... | |
| LocalOrdinal | sumIntoLocalValues (const LocalOrdinal localRow, const ArrayView< const LocalOrdinal > &cols, const ArrayView< const Scalar > &vals) |
| Sum into one or more sparse matrix entries, using local indices. More... | |
| void | setAllToScalar (const Scalar &alpha) |
Set all matrix entries equal to alpha. More... | |
| void | scale (const Scalar &alpha) |
Scale the matrix's values: this := alpha*this. More... | |
| void | setAllValues (const t_RowPtrs &rowPointers, const t_LocalOrdinal_1D &columnIndices, const t_ValuesType &values) |
| Sets the 1D pointer arrays of the graph. More... | |
| void | setAllValues (const ArrayRCP< size_t > &rowPointers, const ArrayRCP< LocalOrdinal > &columnIndices, const ArrayRCP< Scalar > &values) |
| Sets the 1D pointer arrays of the graph. More... | |
| void | getAllValues (ArrayRCP< const size_t > &rowPointers, ArrayRCP< const LocalOrdinal > &columnIndices, ArrayRCP< const Scalar > &values) const |
Transformational methods | |
| void | globalAssemble () |
| Communicate nonlocal contributions to other processes. More... | |
| void | resumeFill (const RCP< ParameterList > ¶ms=null) |
| Resume operations that may change the values or structure of the matrix. More... | |
| void | fillComplete (const RCP< const map_type > &domainMap, const RCP< const map_type > &rangeMap, const RCP< ParameterList > ¶ms=null) |
| Signal that data entry is complete, specifying domain and range maps. More... | |
| void | fillComplete (const RCP< ParameterList > ¶ms=null) |
| Signal that data entry is complete. More... | |
| void | expertStaticFillComplete (const RCP< const map_type > &domainMap, const RCP< const map_type > &rangeMap, const RCP< const import_type > &importer=Teuchos::null, const RCP< const export_type > &exporter=Teuchos::null, const RCP< ParameterList > ¶ms=Teuchos::null) |
| Perform a fillComplete on a matrix that already has data. More... | |
| void | replaceColMap (const Teuchos::RCP< const map_type > &newColMap) |
| Replace the matrix's column Map with the given Map. More... | |
| void | reindexColumns (crs_graph_type *const graph, const Teuchos::RCP< const map_type > &newColMap, const Teuchos::RCP< const import_type > &newImport=Teuchos::null, const bool sortEachRow=true) |
| Reindex the column indices in place, and replace the column Map. Optionally, replace the Import object as well. More... | |
| void | replaceDomainMapAndImporter (const Teuchos::RCP< const map_type > &newDomainMap, Teuchos::RCP< const import_type > &newImporter) |
| Replace the current domain Map and Import with the given objects. More... | |
| virtual void | removeEmptyProcessesInPlace (const Teuchos::RCP< const map_type > &newMap) |
| Remove processes owning zero rows from the Maps and their communicator. More... | |
Methods implementing RowMatrix | |
| RCP< const Comm< int > > | getComm () const |
| The communicator over which the matrix is distributed. More... | |
| RCP< node_type > | getNode () const |
| The Kokkos Node instance. More... | |
| RCP< const map_type > | getRowMap () const |
| The Map that describes the row distribution in this matrix. More... | |
| RCP< const map_type > | getColMap () const |
| The Map that describes the column distribution in this matrix. More... | |
| RCP< const RowGraph < LocalOrdinal, GlobalOrdinal, node_type > > | getGraph () const |
| This matrix's graph, as a RowGraph. More... | |
| RCP< const crs_graph_type > | getCrsGraph () const |
| This matrix's graph, as a CrsGraph. More... | |
| k_local_matrix_type | getLocalMatrix () const |
| Return the underlying local kokkos mtx. More... | |
| global_size_t | getGlobalNumRows () const |
| Number of global elements in the row map of this matrix. More... | |
| global_size_t | getGlobalNumCols () const |
| The number of global columns in the matrix. More... | |
| size_t | getNodeNumRows () const |
| The number of matrix rows owned by the calling process. More... | |
| size_t | getNodeNumCols () const |
| The number of columns connected to the locally owned rows of this matrix. More... | |
| GlobalOrdinal | getIndexBase () const |
| The index base for global indices for this matrix. More... | |
| global_size_t | getGlobalNumEntries () const |
| The global number of entries in this matrix. More... | |
| size_t | getNodeNumEntries () const |
| The local number of entries in this matrix. More... | |
| size_t | getNumEntriesInGlobalRow (GlobalOrdinal globalRow) const |
| Returns the current number of entries on this node in the specified global row. More... | |
| size_t | getNumEntriesInLocalRow (LocalOrdinal localRow) const |
| Returns the current number of entries on this node in the specified local row. More... | |
| global_size_t | getGlobalNumDiags () const |
| Returns the number of global diagonal entries, based on global row/column index comparisons. More... | |
| size_t | getNodeNumDiags () const |
| Returns the number of local diagonal entries, based on global row/column index comparisons. More... | |
| size_t | getGlobalMaxNumRowEntries () const |
| Returns the maximum number of entries across all rows/columns on all nodes. More... | |
| size_t | getNodeMaxNumRowEntries () const |
| Returns the maximum number of entries across all rows/columns on this node. More... | |
| bool | hasColMap () const |
| Indicates whether the matrix has a well-defined column map. More... | |
| bool | isLowerTriangular () const |
| Indicates whether the matrix is lower triangular. More... | |
| bool | isUpperTriangular () const |
| Indicates whether the matrix is upper triangular. More... | |
| bool | isLocallyIndexed () const |
| Whether the matrix is locally indexed on the calling process. More... | |
| bool | isGloballyIndexed () const |
| Whether the matrix is globally indexed on the calling process. More... | |
| bool | isFillComplete () const |
| Whether the matrix is fill complete. More... | |
| bool | isFillActive () const |
| Whether the matrix is not fill complete. More... | |
| bool | isStorageOptimized () const |
Returns true if storage has been optimized. More... | |
| ProfileType | getProfileType () const |
Returns true if the matrix was allocated with static data structures. More... | |
| bool | isStaticGraph () const |
| Indicates that the graph is static, so that new entries cannot be added to this matrix. More... | |
| ScalarTraits< Scalar > ::magnitudeType | getFrobeniusNorm () const |
| Compute and return the Frobenius norm of the matrix. More... | |
| virtual bool | supportsRowViews () const |
Returns true if getLocalRowView() and getGlobalRowView() are valid for this class. More... | |
| void | getGlobalRowCopy (GlobalOrdinal GlobalRow, const ArrayView< GlobalOrdinal > &Indices, const ArrayView< Scalar > &Values, size_t &NumEntries) const |
| Extract a list of entries in a specified global row of this matrix. Put into pre-allocated storage. More... | |
| void | getLocalRowCopy (LocalOrdinal LocalRow, const ArrayView< LocalOrdinal > &Indices, const ArrayView< Scalar > &Values, size_t &NumEntries) const |
| Extract a list of entries in a specified local row of the matrix. Put into storage allocated by calling routine. More... | |
| void | getGlobalRowView (GlobalOrdinal GlobalRow, ArrayView< const GlobalOrdinal > &indices, ArrayView< const Scalar > &values) const |
| Get a constant, nonpersisting view of a row of this matrix, using global row and column indices. More... | |
| void | getLocalRowView (LocalOrdinal LocalRow, ArrayView< const LocalOrdinal > &indices, ArrayView< const Scalar > &values) const |
| Get a constant, nonpersisting view of a row of this matrix, using local row and column indices. More... | |
| void | getLocalDiagCopy (Vector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &diag) const |
| Get a copy of the diagonal entries of the matrix. More... | |
| void | getLocalDiagOffsets (Teuchos::ArrayRCP< size_t > &offsets) const |
| Get offsets of the diagonal entries in the matrix. More... | |
| void | getLocalDiagCopy (Vector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &diag, const Teuchos::ArrayView< const size_t > &offsets) const |
| Variant of getLocalDiagCopy() that uses precomputed offsets. More... | |
| void | leftScale (const Vector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &x) |
| void | rightScale (const Vector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &x) |
Advanced templated methods | |
| template<class DomainScalar , class RangeScalar > | |
| void | localMultiply (const MultiVector< DomainScalar, LocalOrdinal, GlobalOrdinal, node_type > &X, MultiVector< RangeScalar, LocalOrdinal, GlobalOrdinal, node_type > &Y, Teuchos::ETransp trans, RangeScalar alpha, RangeScalar beta) const |
| Compute a sparse matrix-MultiVector product local to each process. More... | |
| template<class DomainScalar , class RangeScalar > | |
| void | localGaussSeidel (const MultiVector< DomainScalar, LocalOrdinal, GlobalOrdinal, node_type > &B, MultiVector< RangeScalar, LocalOrdinal, GlobalOrdinal, node_type > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &D, const RangeScalar &dampingFactor, const KokkosClassic::ESweepDirection direction) const |
Gauss-Seidel or SOR on  . More... | |
| template<class DomainScalar , class RangeScalar > | |
| void | reorderedLocalGaussSeidel (const MultiVector< DomainScalar, LocalOrdinal, GlobalOrdinal, node_type > &B, MultiVector< RangeScalar, LocalOrdinal, GlobalOrdinal, node_type > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &D, const ArrayView< LocalOrdinal > &rowIndices, const RangeScalar &dampingFactor, const KokkosClassic::ESweepDirection direction) const |
| Reordered Gauss-Seidel or SOR on . More... | |
| template<class DomainScalar , class RangeScalar > | |
| void | localSolve (const MultiVector< RangeScalar, LocalOrdinal, GlobalOrdinal, node_type > &Y, MultiVector< DomainScalar, LocalOrdinal, GlobalOrdinal, node_type > &X, Teuchos::ETransp trans) const |
| Solves a linear system when the underlying matrix is triangular. More... | |
| template<class T > | |
| RCP< CrsMatrix< T, LocalOrdinal, GlobalOrdinal, node_type > > | convert () const |
| Returns another CrsMatrix with the same entries, but represented as a different scalar type. More... | |
Methods implementing Operator | |
| void | apply (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &X, MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &Y, Teuchos::ETransp mode=Teuchos::NO_TRANS, Scalar alpha=ScalarTraits< Scalar >::one(), Scalar beta=ScalarTraits< Scalar >::zero()) const |
| Compute a sparse matrix-MultiVector multiply. More... | |
| bool | hasTransposeApply () const |
| Whether apply() allows applying the transpose or conjugate transpose. More... | |
| RCP< const map_type > | getDomainMap () const |
| The domain Map of this operator. More... | |
| RCP< const map_type > | getRangeMap () const |
| The range Map of this operator. More... | |
Other "apply"-like methods | |
| void | gaussSeidel (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &B, MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &D, const Scalar &dampingFactor, const ESweepDirection direction, const int numSweeps) const |
| "Hybrid" Jacobi + (Gauss-Seidel or SOR) on . More... | |
| void | reorderedGaussSeidel (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &B, MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &D, const ArrayView< LocalOrdinal > &rowIndices, const Scalar &dampingFactor, const ESweepDirection direction, const int numSweeps) const |
| Reordered "Hybrid" Jacobi + (Gauss-Seidel or SOR) on . More... | |
| void | gaussSeidelCopy (MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &B, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &D, const Scalar &dampingFactor, const ESweepDirection direction, const int numSweeps, const bool zeroInitialGuess) const |
| Version of gaussSeidel(), with fewer requirements on X. More... | |
| void | reorderedGaussSeidelCopy (MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &B, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &D, const ArrayView< LocalOrdinal > &rowIndices, const Scalar &dampingFactor, const ESweepDirection direction, const int numSweeps, const bool zeroInitialGuess) const |
| Version of reorderedGaussSeidel(), with fewer requirements on X. More... | |
| virtual Teuchos::RCP < RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, node_type > > | add (const Scalar &alpha, const RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &A, const Scalar &beta, const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, node_type > > &domainMap, const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, node_type > > &rangeMap, const Teuchos::RCP< Teuchos::ParameterList > ¶ms) const |
Implementation of RowMatrix::add: return alpha*A + beta*this. More... | |
Implementation of Teuchos::Describable interface | |
| std::string | description () const |
| A simple one-line description of this object. More... | |
| void | describe (Teuchos::FancyOStream &out, const Teuchos::EVerbosityLevel verbLevel=Teuchos::Describable::verbLevel_default) const |
| Print the object with some verbosity level to an FancyOStream object. More... | |
Implementation of DistObject interface | |
| virtual bool | checkSizes (const SrcDistObject &source) |
| Compare the source and target (this) objects for compatibility. More... | |
| virtual void | copyAndPermute (const SrcDistObject &source, size_t numSameIDs, const ArrayView< const LocalOrdinal > &permuteToLIDs, const ArrayView< const LocalOrdinal > &permuteFromLIDs) |
| Perform copies and permutations that are local to this process. More... | |
| virtual void | packAndPrepare (const SrcDistObject &source, const Teuchos::ArrayView< const LocalOrdinal > &exportLIDs, Teuchos::Array< char > &exports, const Teuchos::ArrayView< size_t > &numPacketsPerLID, size_t &constantNumPackets, Distributor &distor) |
| Perform any packing or preparation required for communication. More... | |
| void | unpackAndCombine (const Teuchos::ArrayView< const LocalOrdinal > &importLIDs, const Teuchos::ArrayView< const char > &imports, const Teuchos::ArrayView< size_t > &numPacketsPerLID, size_t constantNumPackets, Distributor &distor, CombineMode combineMode) |
| Unpack the imported column indices and values, and combine into matrix. More... | |
Implementation of Packable interface | |
| virtual void | pack (const Teuchos::ArrayView< const LocalOrdinal > &exportLIDs, Teuchos::Array< char > &exports, const Teuchos::ArrayView< size_t > &numPacketsPerLID, size_t &constantNumPackets, Distributor &distor) const |
| Pack this object's data for an Import or Export. More... | |
Public methods for redistributing data | |
| void | doImport (const SrcDistObject &source, const Import< LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > > &importer, CombineMode CM) |
| Import data into this object using an Import object ("forward mode"). More... | |
| void | doImport (const SrcDistObject &source, const Export< LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > > &exporter, CombineMode CM) |
| Import data into this object using an Export object ("reverse mode"). More... | |
| void | doExport (const SrcDistObject &source, const Export< LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > > &exporter, CombineMode CM) |
| Export data into this object using an Export object ("forward mode"). More... | |
| void | doExport (const SrcDistObject &source, const Import< LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > > &importer, CombineMode CM) |
| Export data into this object using an Import object ("reverse mode"). More... | |
Attribute accessor methods | |
| bool | isDistributed () const |
| Whether this is a globally distributed object. More... | |
| virtual Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode < DeviceType > > > | getMap () const |
| The Map describing the parallel distribution of this object. More... | |
I/O methods | |
| void | print (std::ostream &os) const |
| Print this object to the given output stream. More... | |
Methods for use only by experts | |
| virtual void | removeEmptyProcessesInPlace (const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > > > &newMap) |
| Remove processes which contain no elements in this object's Map. More... | |
Protected Member Functions | |
| void | allocateValues (ELocalGlobal lg, GraphAllocationStatus gas) |
| Allocate values (and optionally indices) using the Node. More... | |
| void | sortEntries () |
| Sort the entries of each row by their column indices. More... | |
| void | mergeRedundantEntries () |
| Merge entries in each row with the same column indices. More... | |
| void | clearGlobalConstants () |
| Clear matrix properties that require collectives. More... | |
| void | computeGlobalConstants () |
| Compute matrix properties that require collectives. More... | |
| Teuchos::RCP< MV > | getColumnMapMultiVector (const MV &X_domainMap, const bool force=false) const |
| Create a (or fetch a cached) column Map MultiVector. More... | |
| Teuchos::RCP< MV > | getRowMapMultiVector (const MV &Y_rangeMap, const bool force=false) const |
| Create a (or fetch a cached) row Map MultiVector. More... | |
| void | applyNonTranspose (const MV &X_in, MV &Y_in, Scalar alpha, Scalar beta) const |
Special case of apply() for mode == Teuchos::NO_TRANS. More... | |
| void | applyTranspose (const MV &X_in, MV &Y_in, const Teuchos::ETransp mode, Scalar alpha, Scalar beta) const |
Special case of apply() for mode != Teuchos::NO_TRANS. More... | |
| Teuchos::ArrayView< const Scalar > | getView (RowInfo rowinfo) const |
| Constant view of all entries (including extra space) in the given row. More... | |
| Teuchos::ArrayView< Scalar > | getViewNonConst (RowInfo rowinfo) |
| Nonconst view of all entries (including extra space) in the given row. More... | |
| void | fillLocalMatrix (const Teuchos::RCP< Teuchos::ParameterList > ¶ms) |
| Fill data into the local matrix. More... | |
| void | fillLocalGraphAndMatrix (const Teuchos::RCP< Teuchos::ParameterList > ¶ms) |
| Fill data into the local graph and matrix. More... | |
| void | checkInternalState () const |
| Check that this object's state is sane; throw if it's not. More... | |
| virtual size_t | constantNumberOfPackets () const |
| Whether the implementation's instance promises always to have a constant number of packets per LID, and if so, how many packets per LID there are. More... | |
| virtual void | doTransfer (const SrcDistObject &src, CombineMode CM, size_t numSameIDs, const Teuchos::ArrayView< const LocalOrdinal > &permuteToLIDs, const Teuchos::ArrayView< const LocalOrdinal > &permuteFromLIDs, const Teuchos::ArrayView< const LocalOrdinal > &remoteLIDs, const Teuchos::ArrayView< const LocalOrdinal > &exportLIDs, Distributor &distor, ReverseOption revOp) |
| Redistribute data across memory images. More... | |
| virtual void | createViews () const |
| Hook for creating a const view. More... | |
| virtual void | createViewsNonConst (KokkosClassic::ReadWriteOption rwo) |
| Hook for creating a nonconst view. More... | |
| virtual void | releaseViews () const |
| Hook for releasing views. More... | |
Protected Attributes | |
| Teuchos::RCP< MV > | importMV_ |
| Column Map MultiVector used in apply() and gaussSeidel(). More... | |
| Teuchos::RCP< MV > | exportMV_ |
| Row Map MultiVector used in apply(). More... | |
| k_local_matrix_type | k_lclMatrix_ |
| The local sparse matrix. More... | |
| Details::EStorageStatus | storageStatus_ |
| Status of the matrix's storage, when not in a fill-complete state. More... | |
| bool | fillComplete_ |
| Whether the matrix is fill complete. More... | |
| std::map< GlobalOrdinal, std::pair< Teuchos::Array < GlobalOrdinal > , Teuchos::Array< Scalar > > > | nonlocals_ |
| Nonlocal data added using insertGlobalValues(). More... | |
| Magnitude | frobNorm_ |
| Cached Frobenius norm of the (global) matrix. More... | |
| Teuchos::RCP< const Map < LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode < DeviceType > > > | map_ |
| The Map over which this object is distributed. More... | |
| Teuchos::Array< char > | imports_ |
| Buffer into which packed data are imported (received from other processes). More... | |
| Teuchos::Array< size_t > | numImportPacketsPerLID_ |
| Number of packets to receive for each receive operation. More... | |
| Teuchos::Array< char > | exports_ |
| Buffer from which packed data are exported (sent to other processes). More... | |
| Teuchos::Array< size_t > | numExportPacketsPerLID_ |
| Number of packets to send for each send operation. More... | |
(Global) graph pointers | |
We keep two graph pointers in order to maintain const correctness. myGraph_ is a graph which we create internally. Operations that change the sparsity structure also modify myGraph_. If myGraph_ != null, then staticGraph_ == myGraph_ pointerwise (we set the pointers equal to each other when we create myGraph_). myGraph_ is only null if this CrsMatrix was created using the constructor with a const CrsGraph input argument. In this case, staticGraph_ is set to the input CrsGraph. | |
| RCP< const Graph > | staticGraph_ |
| RCP< Graph > | myGraph_ |
Sparse matrix values. | |
values1D_ represents the values assuming "1-D" compressed sparse row storage. values2D_ represents the values as an array of arrays, one (inner) array per row of the sparse matrix. Before allocation, both arrays are null. After allocation, one is null. If static allocation, then values2D_ is null. If dynamic allocation, then values1D_ is null. The allocation always matches that of graph_, as the graph does the allocation for the matrix. | |
| ArrayRCP< Scalar > | values1D_ |
| t_ValuesType | k_values1D_ |
| ArrayRCP< Array< Scalar > > | values2D_ |
Friends | |
| template<class CrsMatrixType > | |
| Teuchos::RCP< CrsMatrixType > | importAndFillCompleteCrsMatrix (const Teuchos::RCP< const CrsMatrixType > &sourceMatrix, const Import< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > &importer, const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > &domainMap, const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > &rangeMap, const Teuchos::RCP< Teuchos::ParameterList > ¶ms) |
| Nonmember CrsMatrix constructor that fuses Import and fillComplete(). More... | |
| template<class CrsMatrixType > | |
| Teuchos::RCP< CrsMatrixType > | exportAndFillCompleteCrsMatrix (const Teuchos::RCP< const CrsMatrixType > &sourceMatrix, const Export< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > &exporter, const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > &domainMap, const Teuchos::RCP< const Map< typename CrsMatrixType::local_ordinal_type, typename CrsMatrixType::global_ordinal_type, typename CrsMatrixType::node_type > > &rangeMap, const Teuchos::RCP< Teuchos::ParameterList > ¶ms) |
| Nonmember CrsMatrix constructor that fuses Export and fillComplete(). More... | |
Constructors and destructor | |
| template<class S2 , class LO2 , class GO2 , class N2 > | |
| class | CrsMatrix |
| CrsMatrix (const Teuchos::RCP< const map_type > &rowMap, size_t maxNumEntriesPerRow, ProfileType pftype=DynamicProfile, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) | |
| Constructor specifying fixed number of entries for each row. More... | |
| CrsMatrix (const Teuchos::RCP< const map_type > &rowMap, const ArrayRCP< const size_t > &NumEntriesPerRowToAlloc, ProfileType pftype=DynamicProfile, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) | |
| Constructor specifying (possibly different) number of entries in each row. More... | |
| CrsMatrix (const Teuchos::RCP< const map_type > &rowMap, const Teuchos::RCP< const map_type > &colMap, size_t maxNumEntriesPerRow, ProfileType pftype=DynamicProfile, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) | |
| Constructor specifying column Map and fixed number of entries for each row. More... | |
| CrsMatrix (const Teuchos::RCP< const map_type > &rowMap, const Teuchos::RCP< const map_type > &colMap, const ArrayRCP< const size_t > &NumEntriesPerRowToAlloc, ProfileType pftype=DynamicProfile, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) | |
| Constructor specifying column Map and number of entries in each row. More... | |
| CrsMatrix (const Teuchos::RCP< const crs_graph_type > &graph, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) | |
| Constructor specifying a previously constructed graph. More... | |
| CrsMatrix (const RCP< const map_type > &rowMap, const RCP< const map_type > &colMap, const t_RowPtrs &rowPointers, const t_LocalOrdinal_1D &columnIndices, const t_ValuesType &values, const RCP< ParameterList > ¶ms=null) | |
| Constructor specifying column Map and arrays containing the matrix in sorted local indices. More... | |
| CrsMatrix (const RCP< const map_type > &rowMap, const RCP< const map_type > &colMap, const ArrayRCP< size_t > &rowPointers, const ArrayRCP< LocalOrdinal > &columnIndices, const ArrayRCP< Scalar > &values, const RCP< ParameterList > ¶ms=null) | |
| Constructor specifying column Map and arrays containing the matrix in sorted, local ids. More... | |
| CrsMatrix (const RCP< const map_type > &rowMap, const RCP< const map_type > &colMap, const k_local_matrix_type &lclMatrix, const RCP< Teuchos::ParameterList > ¶ms=null) | |
| Constructor specifying column Map and a local matrix, which the resulting CrsMatrix views. More... | |
| template<class Node2 > | |
| Teuchos::RCP< CrsMatrix < Scalar, LocalOrdinal, GlobalOrdinal, Node2 > > | clone (const Teuchos::RCP< Node2 > &node2, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=null) const |
| Create a deep copy of this CrsMatrix, where the copy may have a different Node type. More... | |
| virtual | ~CrsMatrix () |
| Destructor. More... | |
Partial specialization of CrsMatrix for the new Kokkos wrapper Nodes.
This implements the "Kokkos refactor" version of CrsMatrix. For full documentation, see the "classic" version of CrsMatrix.
Definition at line 63 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef Scalar Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::scalar_type |
This class' first template parameter; the type of entries in the matrix.
Definition at line 81 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef LocalOrdinal Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::local_ordinal_type |
This class' second template parameter; the type of local indices.
Definition at line 83 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef GlobalOrdinal Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::global_ordinal_type |
This class' third template parameter; the type of global indices.
Definition at line 85 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef DeviceType Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::device_type |
This class' fourth template parameter; the Kokkos device type.
Definition at line 87 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef Kokkos::Compat::KokkosDeviceWrapperNode<DeviceType> Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::node_type |
The Kokkos Node type used by this class.
This type depends on the DeviceType template parameter. In this, the Kokkos refactor version of Tpetra, it exists only for backwards compatibility.
Definition at line 93 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef Map<LocalOrdinal, GlobalOrdinal, node_type> Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::map_type |
The Map specialization suitable for this CrsMatrix specialization.
Definition at line 96 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef Import<LocalOrdinal, GlobalOrdinal, node_type> Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::import_type |
The Import specialization suitable for this CrsMatrix specialization.
Definition at line 99 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef Export<LocalOrdinal, GlobalOrdinal, node_type> Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::export_type |
The Export specialization suitable for this CrsMatrix specialization.
Definition at line 102 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef CrsGraph<LocalOrdinal, GlobalOrdinal, node_type> Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::crs_graph_type |
The CrsGraph specialization suitable for this CrsMatrix specialization.
Definition at line 105 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
inherited |
The type of each datum being sent or received in an Import or Export.
Note that this type does not always correspond to the Scalar template parameter of subclasses.
Definition at line 183 of file Tpetra_DistObject_decl.hpp.
|
protectedinherited |
Whether the data transfer should be performed in forward or reverse mode.
"Reverse mode" means calling doExport() with an Import object, or calling doImport() with an Export object. "Forward mode" means calling doExport() with an Export object, or calling doImport() with an Import object.
Definition at line 417 of file Tpetra_DistObject_decl.hpp.
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::CrsMatrix | ( | const Teuchos::RCP< const map_type > & | rowMap, |
| size_t | maxNumEntriesPerRow, | ||
| ProfileType | pftype = DynamicProfile, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Constructor specifying fixed number of entries for each row.
| rowMap | [in] Distribution of rows of the matrix. |
| maxNumEntriesPerRow | [in] Maximum number of matrix entries per row. If pftype==DynamicProfile, this is only a hint, and you can set this to zero without affecting correctness. If pftype==StaticProfile, this sets the amount of storage allocated, and you cannot exceed this number of entries in any row. |
| pftype | [in] Whether to allocate storage dynamically (DynamicProfile) or statically (StaticProfile). |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 58 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::CrsMatrix | ( | const Teuchos::RCP< const map_type > & | rowMap, |
| const ArrayRCP< const size_t > & | NumEntriesPerRowToAlloc, | ||
| ProfileType | pftype = DynamicProfile, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Constructor specifying (possibly different) number of entries in each row.
| rowMap | [in] Distribution of rows of the matrix. |
| NumEntriesPerRowToAlloc | [in] Maximum number of matrix entries to allocate for each row. If pftype==DynamicProfile, this is only a hint. If pftype==StaticProfile, this sets the amount of storage allocated, and you cannot exceed the allocated number of entries for any row. |
| pftype | [in] Whether to allocate storage dynamically (DynamicProfile) or statically (StaticProfile). |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 87 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::CrsMatrix | ( | const Teuchos::RCP< const map_type > & | rowMap, |
| const Teuchos::RCP< const map_type > & | colMap, | ||
| size_t | maxNumEntriesPerRow, | ||
| ProfileType | pftype = DynamicProfile, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Constructor specifying column Map and fixed number of entries for each row.
The column Map will be used to filter any matrix entries inserted using insertLocalValues() or insertGlobalValues().
| rowMap | [in] Distribution of rows of the matrix. |
| colMap | [in] Distribution of columns of the matrix. |
| maxNumEntriesPerRow | [in] Maximum number of matrix entries per row. If pftype==DynamicProfile, this is only a hint, and you can set this to zero without affecting correctness. If pftype==StaticProfile, this sets the amount of storage allocated, and you cannot exceed this number of entries in any row. |
| pftype | [in] Whether to allocate storage dynamically (DynamicProfile) or statically (StaticProfile). |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 117 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::CrsMatrix | ( | const Teuchos::RCP< const map_type > & | rowMap, |
| const Teuchos::RCP< const map_type > & | colMap, | ||
| const ArrayRCP< const size_t > & | NumEntriesPerRowToAlloc, | ||
| ProfileType | pftype = DynamicProfile, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Constructor specifying column Map and number of entries in each row.
The column Map will be used to filter any matrix indices inserted using insertLocalValues() or insertGlobalValues().
| rowMap | [in] Distribution of rows of the matrix. |
| colMap | [in] Distribution of columns of the matrix. |
| NumEntriesPerRowToAlloc | [in] Maximum number of matrix entries to allocate for each row. If pftype==DynamicProfile, this is only a hint. If pftype==StaticProfile, this sets the amount of storage allocated, and you cannot exceed the allocated number of entries for any row. |
| pftype | [in] Whether to allocate storage dynamically (DynamicProfile) or statically (StaticProfile). |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 156 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
explicit |
Constructor specifying a previously constructed graph.
Calling this constructor fixes the graph structure of the sparse matrix. We say in this case that the matrix has a "static graph." If you create a CrsMatrix with this constructor, you are not allowed to insert new entries into the matrix, but you are allowed to change values in the matrix.
The given graph must be fill complete. Note that calling resumeFill() on the graph makes it not fill complete, even if you had previously called fillComplete() on the graph. In that case, you must call fillComplete() on the graph again before invoking this CrsMatrix constructor.
This constructor is marked explicit so that you can't create a CrsMatrix by accident when passing a CrsGraph into a function that takes a CrsMatrix.
| graph | [in] The graph structure of the sparse matrix. The graph must be fill complete. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::CrsMatrix | ( | const RCP< const map_type > & | rowMap, |
| const RCP< const map_type > & | colMap, | ||
| const t_RowPtrs & | rowPointers, | ||
| const t_LocalOrdinal_1D & | columnIndices, | ||
| const t_ValuesType & | values, | ||
| const RCP< ParameterList > & | params = null |
||
| ) |
Constructor specifying column Map and arrays containing the matrix in sorted local indices.
| rowMap | [in] Distribution of rows of the matrix. |
| colMap | [in] Distribution of columns of the matrix. |
| rowPointers | [in] The beginning of each row in the matrix, as in a CSR "rowptr" array. The length of this vector should be equal to the number of rows in the graph, plus one. This last entry should store the nunber of nonzeros in the matrix. |
| columnIndices | [in] The local indices of the columns, as in a CSR "colind" array. The length of this vector should be equal to the number of unknowns in the matrix. |
| values | [in] The local entries in the matrix, as in a CSR "vals" array. The length of this vector should be equal to the number of unknowns in the matrix. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 217 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::CrsMatrix | ( | const RCP< const map_type > & | rowMap, |
| const RCP< const map_type > & | colMap, | ||
| const ArrayRCP< size_t > & | rowPointers, | ||
| const ArrayRCP< LocalOrdinal > & | columnIndices, | ||
| const ArrayRCP< Scalar > & | values, | ||
| const RCP< ParameterList > & | params = null |
||
| ) |
Constructor specifying column Map and arrays containing the matrix in sorted, local ids.
| rowMap | [in] Distribution of rows of the matrix. |
| colMap | [in] Distribution of columns of the matrix. |
| rowPointers | [in] The beginning of each row in the matrix, as in a CSR "rowptr" array. The length of this vector should be equal to the number of rows in the graph, plus one. This last entry should store the nunber of nonzeros in the matrix. |
| columnIndices | [in] The local indices of the columns, as in a CSR "colind" array. The length of this vector should be equal to the number of unknowns in the matrix. |
| values | [in] The local entries in the matrix, as in a CSR "vals" array. The length of this vector should be equal to the number of unknowns in the matrix. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 247 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::CrsMatrix | ( | const RCP< const map_type > & | rowMap, |
| const RCP< const map_type > & | colMap, | ||
| const k_local_matrix_type & | lclMatrix, | ||
| const RCP< Teuchos::ParameterList > & | params = null |
||
| ) |
Constructor specifying column Map and a local matrix, which the resulting CrsMatrix views.
Unlike most other CrsMatrix constructors, successful completion of this constructor will result in a fill-complete matrix.
| rowMap | [in] Distribution of rows of the matrix. |
| colMap | [in] Distribution of columns of the matrix. |
| lclMatrix | [in] A local CrsMatrix containing all local matrix values as well as a local graph. The graph's local row indices must come from the specified row Map, and its local column indices must come from the specified column Map. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 280 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Destructor.
Definition at line 338 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
inline |
Create a deep copy of this CrsMatrix, where the copy may have a different Node type.
| node2 | [in] Kokkos Node instance for the returned copy. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Parameters to params:
true, create the copy with a static allocation profile. If false, use a dynamic allocation profile.true, fill clone using this matrix's column Map and local indices. This matrix must have a column Map in order for this to work. If false, fill clone using global indices. By default, this will use local indices only if this matrix is using local indices.true, call fillComplete() on the cloned CrsMatrix object, with parameters from the input parameters' "CrsMatrix" sublist The domain Map and range Map passed to fillComplete() are those of the map being cloned, if they exist. Otherwise, the row Map is used. Definition at line 358 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::insertGlobalValues | ( | const GlobalOrdinal | globalRow, |
| const ArrayView< const GlobalOrdinal > & | cols, | ||
| const ArrayView< const Scalar > & | vals | ||
| ) |
Insert one or more entries into the matrix, using global indices.
| globalRow | [in] Global index of the row into which to insert the entries. |
| cols | [in] Global indices of the columns into which to insert the entries. |
| values | [in] Values to insert into the above columns. |
For all k in 0, ..., col.size()-1, insert the value values[k] into entry (globalRow, cols[k]) of the matrix. If that entry already exists, add the new value to the old value.
This is a local operation. It does not communicate (using MPI). If row globalRow is owned by the calling process, the entries will be inserted immediately. Otherwise, if that row is not owned by the calling process, then the entries will be stored locally for now, and only communicated to the process that owns the row when either fillComplete() or globalAssemble() is called. If that process already has an entry, the incoming value will be added to the old value, just as if it were inserted on the owning process. If the matrix has a column Map (hasColMap() == true), and if globalRow is owned by process p, then it is forbidden to insert column indices that are not in the column Map on process p. Tpetra will test the input column indices to ensure this is the case, but if globalRow is not owned by the calling process, the test will be deferred until the next call to globalAssemble() or fillComplete().
It is legal to call this method whether the matrix's column indices are globally or locally indexed. If the matrix's column indices are locally indexed (isLocallyIndexed() == true), then this method will convert the input global column indices to local column indices.
For better performance when filling entries into a sparse matrix, consider the following tips:
Definition at line 1601 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::insertLocalValues | ( | const LocalOrdinal | localRow, |
| const ArrayView< const LocalOrdinal > & | cols, | ||
| const ArrayView< const Scalar > & | vals | ||
| ) |
Insert one or more entries into the matrix, using local indices.
| LocalRow | [in] Local index of the row into which to insert the entries. It must be owned by the row Map on the calling process. |
| cols | [in] Local indices of the columns into which to insert the entries. All of the column indices must be owned by the column Map on the calling process. |
| values | [in] Values to insert into the above columns. |
For all k in 0, ..., cols.size()-1, insert the value values[k] into entry (globalRow, cols[k]) of the matrix. If that entry already exists, add the new value to the old value.
In order to call this method, the matrix must be locally indexed, and it must have a column Map.
For better performance when filling entries into a sparse matrix, consider the following tips:
Definition at line 1385 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| LocalOrdinal Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::replaceGlobalValues | ( | GlobalOrdinal | globalRow, |
| const ArrayView< const GlobalOrdinal > & | cols, | ||
| const ArrayView< const Scalar > & | vals | ||
| ) |
Replace one or more entries' values, using global indices.
| globalRow | [in] Global index of the row in which to replace the entries. This row must be owned by the calling process. |
| cols | [in] Global indices of the columns in which to replace the entries. |
| vals | [in] Values to use for replacing the entries. |
For all k in 0, ..., cols.size()-1, replace the value at entry (globalRow, cols[k]) of the matrix with vals[k]. That entry must exist in the matrix already.
If (globalRow, cols[k]) corresponds to an entry that is duplicated in this matrix row (likely because it was inserted more than once and fillComplete() has not been called in the interim), the behavior of this method is not defined.
If the returned value N satisfies
0 <= N < cols.size(),
then cols.size() - N of the entries of cols are not valid global column indices. If the returned value is Teuchos::OrdinalTraits<LocalOrdinal>::invalid(), then at least one of the following is true:
! isFillActive () cols.size () != vals.size () Definition at line 2007 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| LocalOrdinal Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::replaceLocalValues | ( | const LocalOrdinal | localRow, |
| const ArrayView< const LocalOrdinal > & | cols, | ||
| const ArrayView< const Scalar > & | vals | ||
| ) |
Replace one or more entries' values, using local indices.
| localRow | [in] local index of the row in which to replace the entries. This row must be owned by the calling process. |
| cols | [in] Local indices of the columns in which to replace the entries. |
| vals | [in] Values to use for replacing the entries. |
For all k in 0, ..., cols.size()-1, replace the value at entry (localRow, cols[k]) of the matrix with vals[k]. That entry must exist in the matrix already.
If the returned value N satisfies
0 <= N < cols.size(),
then cols.size() - N of the entries of cols are not valid local column indices. If the returned value is Teuchos::OrdinalTraits<LocalOrdinal>::invalid(), then at least one of the following is true:
! isFillActive () ! hasColMap () cols.size () != vals.size () Definition at line 1911 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| LocalOrdinal Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::sumIntoGlobalValues | ( | const GlobalOrdinal | globalRow, |
| const ArrayView< const GlobalOrdinal > & | cols, | ||
| const ArrayView< const Scalar > & | vals | ||
| ) |
Sum into one or more sparse matrix entries, using global indices.
This is a local operation; it does not involve communication. However, if you sum into rows not owned by the calling process, it may result in future communication in globalAssemble() (which is called by fillComplete()).
If globalRow is owned by the calling process, then this method performs the sum-into operation right away. Otherwise, if the row is not owned by the calling process, this method defers the sum-into operation until globalAssemble(). That method communicates data for nonowned rows to the processes that own those rows. Then, globalAssemble() does one of the following:
| globalRow | [in] The global index of the row in which to sum into the matrix entries. |
| cols | [in] One or more column indices. |
| vals | [in] One or more values corresponding to those column indices. vals[k] corresponds to cols[k]. |
This method has the same preconditions and return value meaning as replaceGlobalValues() (which see).
Definition at line 2091 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| LocalOrdinal Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::sumIntoLocalValues | ( | const LocalOrdinal | localRow, |
| const ArrayView< const LocalOrdinal > & | cols, | ||
| const ArrayView< const Scalar > & | vals | ||
| ) |
Sum into one or more sparse matrix entries, using local indices.
| localRow | [in] Local index of a row. This row must be owned by the calling process. |
| cols | [in] Local indices of the columns whose entries we want to modify. |
| vals | [in] Values corresponding to the above column indices. vals[k] corresponds to cols[k]. |
This method has the same preconditions and return value meaning as replaceLocalValues() (which see).
Definition at line 2183 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::setAllToScalar | ( | const Scalar & | alpha | ) |
Set all matrix entries equal to alpha.
Definition at line 2584 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::scale | ( | const Scalar & | alpha | ) |
Scale the matrix's values: this := alpha*this.
Definition at line 2539 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::setAllValues | ( | const t_RowPtrs & | rowPointers, |
| const t_LocalOrdinal_1D & | columnIndices, | ||
| const t_ValuesType & | values | ||
| ) |
Sets the 1D pointer arrays of the graph.
hasColMap() == true getGraph() != Teuchos::null Definition at line 2620 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::setAllValues | ( | const ArrayRCP< size_t > & | rowPointers, |
| const ArrayRCP< LocalOrdinal > & | columnIndices, | ||
| const ArrayRCP< Scalar > & | values | ||
| ) |
Sets the 1D pointer arrays of the graph.
hasColMap() == true getGraph() != Teuchos::null FIXME (mfh 24 Feb 2014) Why is the third prerequisites above different than the third prerequisite from the original class? The original is that fillComplete() must have been called.
Definition at line 2650 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::globalAssemble | ( | ) |
Communicate nonlocal contributions to other processes.
Users do not normally need to call this method. fillComplete always calls this method, unless you specifically tell fillComplete to do otherwise by setting its "No Nonlocal
Changes" parameter to true. Thus, it suffices to call fillComplete.
Methods like insertGlobalValues and sumIntoGlobalValues let you add or modify entries in rows that are not owned by the calling process. These entries are called "nonlocal contributions." The methods that allow nonlocal contributions store the entries on the calling process, until globalAssemble is called. globalAssemble sends these nonlocal contributions to the process(es) that own them, where they then become part of the matrix.
This method only does global assembly if there are nonlocal entries on at least one process. It does an all-reduce to find that out. If not, it returns early, without doing any more communication or work.
If you previously inserted into a row which is not owned by any process in the row Map, the behavior of this method is undefined. It may detect the invalid row indices and throw an exception, or it may silently drop the entries inserted into invalid rows. Behavior may vary, depending on whether Tpetra was built with debug checking enabled.
Definition at line 3186 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::resumeFill | ( | const RCP< ParameterList > & | params = null | ) |
Resume operations that may change the values or structure of the matrix.
This method must be called as a collective operation.
Calling fillComplete "freezes" both the values and the structure of the matrix. If you want to modify the matrix again, you must first call resumeFill. You then may not call resumeFill again on that matrix until you first call fillComplete. You may make sequences of fillComplete, resumeFill calls as many times as you wish.
isFillActive() && ! isFillComplete() Definition at line 3495 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::fillComplete | ( | const RCP< const map_type > & | domainMap, |
| const RCP< const map_type > & | rangeMap, | ||
| const RCP< ParameterList > & | params = null |
||
| ) |
Signal that data entry is complete, specifying domain and range maps.
Off-node indices are distributed (via globalAssemble()), indices are sorted, redundant indices are eliminated, and global indices are transformed to local indices.
isFillActive() == true isFillComplete()() == false isFillActive() == false isFillComplete() == trueParameters:
bool): Default is false. If true, the caller promises that no modifications to nonowned rows have happened on any process since the last call to fillComplete. This saves a global all-reduce to check whether any process did a nonlocal insert. Nonlocal changes include any sumIntoGlobalValues or insertGlobalValues call with a row index that is not in the row Map of the calling process.bool): Default is true. makeColMap() (which fillComplete may call) always groups remote GIDs by process rank, so that all remote GIDs with the same owning rank occur contiguously. By default, it always sorts remote GIDs in increasing order within those groups. This behavior differs from Epetra, which does not sort remote GIDs with the same owning process. If you don't want to sort (for compatibility with Epetra), set this parameter to false. This parameter only takes effect if the matrix owns the graph. This is an expert mode parameter ONLY. We make no promises about backwards compatibility of this parameter. It may change or disappear at any time. Definition at line 3565 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::fillComplete | ( | const RCP< ParameterList > & | params = null | ) |
Signal that data entry is complete.
Off-node entries are distributed (via globalAssemble()), repeated entries are summed, and global indices are transformed to local indices.
isFillActive() == true isFillComplete()() == false isFillActive() == false isFillComplete() == true Definition at line 3544 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::expertStaticFillComplete | ( | const RCP< const map_type > & | domainMap, |
| const RCP< const map_type > & | rangeMap, | ||
| const RCP< const import_type > & | importer = Teuchos::null, |
||
| const RCP< const export_type > & | exporter = Teuchos::null, |
||
| const RCP< ParameterList > & | params = Teuchos::null |
||
| ) |
Perform a fillComplete on a matrix that already has data.
The matrix must already have filled local 1-D storage (k_lclInds1D_ and k_rowPtrs_ for the graph, and k_values1D_ in the matrix). If the matrix has been constructed in any other way, this method will throw an exception. This routine is needed to support other Trilinos packages and should not be called by ordinary users.
Definition at line 3723 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::replaceColMap | ( | const Teuchos::RCP< const map_type > & | newColMap | ) |
Replace the matrix's column Map with the given Map.
| newColMap | [in] New column Map. Must be nonnull. |
Definition at line 3085 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::reindexColumns | ( | crs_graph_type *const | graph, |
| const Teuchos::RCP< const map_type > & | newColMap, | ||
| const Teuchos::RCP< const import_type > & | newImport = Teuchos::null, |
||
| const bool | sortEachRow = true |
||
| ) |
Reindex the column indices in place, and replace the column Map. Optionally, replace the Import object as well.
! this->isFillComplete() . NULL, or it is not fill complete: graph == NULL || ! graph->isFillComplete(). | graph | [in] The matrix's graph. If you don't provide this (i.e., if graph == NULL), then the matrix must own its graph, which will be modified in place. (That is, you must not have created the matrix with a constant graph.) If you do provide this, then the method will assume that it is the same graph as the matrix's graph, and the provided graph will be modified in place. |
| newColMap | [in] New column Map. Must be nonnull. |
| newImport | [in] New Import object. Optional; computed if not provided or if null. Computing an Import is expensive, so it is worth providing this if you can. |
| sortEachRow | [in] If true, sort the indices (and their corresponding values) in each row after reindexing. |
Why would you want to use this method? Well, for example, you might need to use an Ifpack2 preconditioner that only accepts a matrix with a certain kind of column Map. Your matrix has the wrong kind of column Map, but you know how to compute the right kind of column Map. You might also know an efficient way to compute an Import object from the current domain Map to the new column Map. (For an instance of the latter, see the Details::makeOptimizedColMapAndImport function in Tpetra_Details_makeOptimizedColMap.hpp.)
Suppose that you created this CrsMatrix with a constant graph; that is, that you called the CrsMatrix constructor that takes a CrsGraph as input:
Now suppose that you want to give A to a preconditioner that can't handle a matrix with an arbitrary column Map (in the example above, origColMap). You first must create a new suitable column Map newColMap, and optionally a new Import object newImport from the matrix's current domain Map to the new column Map. Then, call this method, passing in G (which must not be fill complete) while the matrix is not fill complete. Be sure to save the graph's original Import object; you'll need that later.
Now you may give the matrix A to the preconditioner in question. After doing so, and after you solve the linear system using the preconditioner, you might want to put the matrix back like it originally was. You can do that, too!
Definition at line 3107 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::replaceDomainMapAndImporter | ( | const Teuchos::RCP< const map_type > & | newDomainMap, |
| Teuchos::RCP< const import_type > & | newImporter | ||
| ) |
Replace the current domain Map and Import with the given objects.
| newDomainMap | [in] New domain Map. Must be nonnull. |
| newImporter | [in] Optional Import object. If null, we will compute it. |
isFillComplete() == true. Definition at line 3140 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Remove processes owning zero rows from the Maps and their communicator.
| newMap | [in] This must be the result of calling the removeEmptyProcesses() method on the row Map. If it is not, this method's behavior is undefined. This pointer will be null on excluded processes. |
Definition at line 6258 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The communicator over which the matrix is distributed.
Definition at line 346 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The Kokkos Node instance.
Definition at line 356 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The Map that describes the row distribution in this matrix.
Definition at line 474 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The Map that describes the column distribution in this matrix.
Definition at line 481 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
This matrix's graph, as a RowGraph.
Definition at line 502 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| RCP< const CrsGraph< LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > > > Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::getCrsGraph | ( | ) | const |
This matrix's graph, as a CrsGraph.
Definition at line 510 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
inline |
Return the underlying local kokkos mtx.
Definition at line 1130 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
virtual |
Number of global elements in the row map of this matrix.
This is <it>not</it> the number of rows in the matrix as a mathematical object. This method returns the global sum of the number of local elements in the row map on each processor, which is the row map's getGlobalNumElements(). Since the row map is not one-to-one in general, that global sum could be different than the number of rows in the matrix. If you want the number of rows in the matrix, ask the range map for its global number of elements, using the following code: global_size_t globalNumRows = getRangeMap()->getGlobalNumElements(); This method retains the behavior of Epetra, which also asks the row map for the global number of rows, rather than asking the range map.
Definition at line 418 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The number of global columns in the matrix.
This equals the number of entries in the matrix's domain Map.
Definition at line 423 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The number of matrix rows owned by the calling process.
Note that the sum of all the return values over all processes in the row Map's communicator does not necessarily equal the global number of rows in the matrix, if the row Map is overlapping.
Definition at line 428 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The number of columns connected to the locally owned rows of this matrix.
Throws std::runtime_error if ! hasColMap ().
Definition at line 433 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The index base for global indices for this matrix.
Definition at line 468 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The global number of entries in this matrix.
Definition at line 408 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The local number of entries in this matrix.
Definition at line 413 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Returns the current number of entries on this node in the specified global row.
Returns OrdinalTraits<size_t>::invalid() if the specified global row does not belong to this matrix.
Definition at line 448 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Returns the current number of entries on this node in the specified local row.
Returns OrdinalTraits<size_t>::invalid() if the specified local row is not valid for this matrix.
Definition at line 453 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Returns the number of global diagonal entries, based on global row/column index comparisons.
Undefined if isFillActive().
Definition at line 438 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Returns the number of local diagonal entries, based on global row/column index comparisons.
Undefined if isFillActive().
Definition at line 443 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Returns the maximum number of entries across all rows/columns on all nodes.
Undefined if isFillActive().
Definition at line 458 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Returns the maximum number of entries across all rows/columns on this node.
Undefined if isFillActive().
Definition at line 463 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Indicates whether the matrix has a well-defined column map.
Definition at line 403 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Indicates whether the matrix is lower triangular.
Undefined if isFillActive().
Definition at line 517 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Indicates whether the matrix is upper triangular.
Undefined if isFillActive().
Definition at line 523 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Whether the matrix is locally indexed on the calling process.
The matrix is locally indexed on the calling process if and only if all of the following hold:
The following is always true:
That is, a matrix may be neither locally nor globally indexed, but it can never be both. Furthermore a matrix that is not fill complete, might have some processes that are neither locally nor globally indexed, and some processes that are globally indexed. The processes that are neither do not have any entries.
Definition at line 393 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Whether the matrix is globally indexed on the calling process.
The matrix is globally indexed on the calling process if and only if all of the following hold:
The following is always true:
That is, a matrix may be neither locally nor globally indexed, but it can never be both. Furthermore a matrix that is not fill complete, might have some processes that are neither locally nor globally indexed, and some processes that are globally indexed. The processes that are neither do not have any entries.
Definition at line 398 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Whether the matrix is fill complete.
A matrix is fill complete (or "in compute mode") when fillComplete() has been called without an intervening call to resumeFill(). A matrix must be fill complete in order to call computational kernels like sparse matrix-vector multiply and sparse triangular solve. A matrix must be not fill complete ("in edit mode") in order to call methods that insert, modify, or remove entries.
The following are always true:
A matrix starts out (after its constructor returns) as not fill complete. It becomes fill complete after fillComplete() returns, and becomes not fill complete again if resumeFill() is called. Some methods like clone() and some of the "nonmember constructors" (like importAndFillComplete() and exportAndFillComplete()) may return a fill-complete matrix.
Definition at line 374 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| bool Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::isFillActive | ( | ) | const |
Whether the matrix is not fill complete.
A matrix is fill complete (or "in compute mode") when fillComplete() has been called without an intervening call to resumeFill(). A matrix must be fill complete in order to call computational kernels like sparse matrix-vector multiply and sparse triangular solve. A matrix must be not fill complete ("in edit mode") in order to call methods that insert, modify, or remove entries.
The following are always true:
A matrix starts out (after its constructor returns) as not fill complete. It becomes fill complete after fillComplete() returns, and becomes not fill complete again if resumeFill() is called. Some methods like clone() and some of the "nonmember constructors" (like importAndFillComplete() and exportAndFillComplete()) may return a fill-complete matrix.
Definition at line 383 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| bool Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::isStorageOptimized | ( | ) | const |
Returns true if storage has been optimized.
Optimized storage means that the allocation of each row is equal to the number of entries. The effect is that a pass through the matrix, i.e., during a mat-vec, requires minimal memory traffic. One limitation of optimized storage is that no new indices can be added to the matrix.
Definition at line 388 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| ProfileType Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::getProfileType | ( | ) | const |
Returns true if the matrix was allocated with static data structures.
Definition at line 365 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| bool Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::isStaticGraph | ( | ) | const |
Indicates that the graph is static, so that new entries cannot be added to this matrix.
Definition at line 529 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Compute and return the Frobenius norm of the matrix.
The Frobenius norm of the matrix is defined as [ |A|_F = {{i,j} |{ij}|^2}. ].
If the matrix is fill complete, then the computed value is cached; the cache is cleared whenever resumeFill() is called. Otherwise, the value is computed every time the method is called.
Definition at line 3020 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Returns true if getLocalRowView() and getGlobalRowView() are valid for this class.
Definition at line 544 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Extract a list of entries in a specified global row of this matrix. Put into pre-allocated storage.
| LocalRow | - (In) Global row number for which indices are desired. |
| Indices | - (Out) Global column indices corresponding to values. |
| Values | - (Out) Matrix values. |
| NumEntries | - (Out) Number of indices. |
Note: A std::runtime_error exception is thrown if either Indices or Values is not large enough to hold the data associated with row GlobalRow. If GlobalRow does not belong to this node, then Indices and Values are unchanged and NumIndices is returned as OrdinalTraits<size_t>::invalid().
Definition at line 2410 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Extract a list of entries in a specified local row of the matrix. Put into storage allocated by calling routine.
| LocalRow | - (In) Local row number for which indices are desired. |
| Indices | - (Out) Local column indices corresponding to values. |
| Values | - (Out) Matrix values. |
| NumIndices | - (Out) Number of indices. |
Note: A std::runtime_error exception is thrown if either Indices or Values is not large enough to hold the data associated with row LocalRow. If LocalRow is not valid for this node, then Indices and Values are unchanged and NumIndices is returned as OrdinalTraits<size_t>::invalid().
isLocallyIndexed()==true or hasColMap() == true Definition at line 2343 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Get a constant, nonpersisting view of a row of this matrix, using global row and column indices.
| GlobalRow | [in] Global index of the row to view. |
| indices | [out] On output: view of the global column indices in the row. |
| values | [out] On output: view of the values in the row. |
isLocallyIndexed () == false indices.size () == this->getNumEntriesInGlobalRow (GlobalRow)If GlobalRow is not a valid global row index on the calling process, then indices is set to null.
Definition at line 2499 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Get a constant, nonpersisting view of a row of this matrix, using local row and column indices.
| LocalRow | [in] Local index of the row to view. |
| indices | [out] On output: view of the local column indices in the row. |
| values | [out] On output: view of the values in the row. |
isGloballyIndexed () == false indices.size () == this->getNumEntriesInLocalRow (LocalRow)If LocalRow is not a valid local row index on the calling process, then indices is set to null.
Definition at line 2463 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Get a copy of the diagonal entries of the matrix.
This method returns a Vector with the same Map as this matrix's row Map. On each process, it contains the diagonal entries owned by the calling process.
Definition at line 2774 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::getLocalDiagOffsets | ( | Teuchos::ArrayRCP< size_t > & | offsets | ) | const |
Get offsets of the diagonal entries in the matrix.
offsets.size() == getNodeNumRows()This method creates an array of offsets of the local diagonal entries in the matrix. This array is suitable for use in the two-argument version of getLocalDiagCopy(). However, its contents are not defined in any other context. For example, you should not rely on offsets[i] being the index of the diagonal entry in the views returned by getLocalRowView(). This may be the case, but it need not be. (For example, we may choose to optimize the lookups down to the optimized storage level, in which case the offsets will be computed with respect to the underlying storage format, rather than with respect to the views.)
Calling any of the following invalidates the output array:
If the matrix has a const ("static") graph, and if that graph is fill complete, then the offsets array remains valid through calls to fillComplete() and resumeFill(). "Invalidates" means that you must call this method again to recompute the offsets.
Definition at line 2680 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::getLocalDiagCopy | ( | Vector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | diag, |
| const Teuchos::ArrayView< const size_t > & | offsets | ||
| ) | const |
Variant of getLocalDiagCopy() that uses precomputed offsets.
This method uses the offsets of the diagonal entries, as precomputed by getLocalDiagOffsets(), to speed up copying the diagonal of the matrix. The offsets must be recomputed if any of the following methods are called:
If the matrix has a const ("static") graph, and if that graph is fill complete, then the offsets array remains valid through calls to fillComplete() and resumeFill().
Definition at line 2850 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Definition at line 2904 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Definition at line 2961 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::localMultiply | ( | const MultiVector< DomainScalar, LocalOrdinal, GlobalOrdinal, node_type > & | X, |
| MultiVector< RangeScalar, LocalOrdinal, GlobalOrdinal, node_type > & | Y, | ||
| Teuchos::ETransp | trans, | ||
| RangeScalar | alpha, | ||
| RangeScalar | beta | ||
| ) | const |
Compute a sparse matrix-MultiVector product local to each process.
This method computes the local part of Y := beta*Y
Op(A) is either 
, 
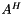(the transpose), or 
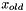(the conjugate transpose). "The local part" means that this method does no communication between processes, even if this is necessary for correctness of the matrix-vector multiply. Use the apply() method if you want to compute the mathematical sparse matrix-vector multiply.This method is mainly of use to Tpetra developers, though some users may find it helpful if they plan to reuse the result of doing an Import on the input MultiVector for several sparse matrix-vector multiplies with matrices that have the same column Map.
When Op(A) is (trans == Teuchos::NO_TRANS), then X's Map must be the same as the column Map of this matrix, and Y's Map must be the same as the row Map of this matrix. We say in this case that X is "post-Imported," and Y is "pre-Exported." When Op(A) is 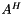or 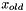(trans is Teuchos::TRANS or Teuchos::CONJ_TRANS, then X's Map must be the same as the row Map of this matrix, and Y's Map must be the same as the column Map of this matrix.
Both X and Y must have constant stride, and they may not alias one another (that is, occupy overlapping space in memory). We may not necessarily check for aliasing, and if we do, we will only do this in a debug build. Aliasing X and Y may cause nondeterministically incorrect results.
This method is templated on the type of entries in both the input MultiVector (DomainScalar) and the output MultiVector (RangeScalar). Thus, this method works for MultiVector objects of arbitrary type. However, this method only performs computation local to each MPI process. Use CrsMatrixMultiplyOp to handle global communication (the Import and Export operations for the input resp. output MultiVector), if you have a matrix with entries of a different type than the input and output MultiVector objects.
If beta == 0, this operation will enjoy overwrite semantics: Y will be overwritten with the result of the multiplication, even if it contains NaN (not-a-number) floating-point entries. Otherwise, the multiply result will be accumulated into Y.
Definition at line 4743 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::localGaussSeidel | ( | const MultiVector< DomainScalar, LocalOrdinal, GlobalOrdinal, node_type > & | B, |
| MultiVector< RangeScalar, LocalOrdinal, GlobalOrdinal, node_type > & | X, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | D, | ||
| const RangeScalar & | dampingFactor, | ||
| const KokkosClassic::ESweepDirection | direction | ||
| ) | const |
Gauss-Seidel or SOR on .
Apply a forward or backward sweep of Gauss-Seidel or Successive Over-Relaxation (SOR) to the linear system(s) . For Gauss-Seidel, set the damping factor omega to 1.
| DomainScalar | The type of entries in the input multivector X. This may differ from the type of entries in A or in B. |
| RangeScalar | The type of entries in the output multivector B. This may differ from the type of entries in A or in X. |
| B | [in] Right-hand side(s). |
| X | [in/out] On input: initial guess(es). On output: result multivector(s). |
| D | [in] Inverse of diagonal entries of the matrix A. |
| omega | [in] SOR damping factor. omega = 1 results in Gauss-Seidel. |
| direction | [in] Sweep direction: KokkosClassic::Forward or KokkosClassic::Backward. ("Symmetric" requires interprocess communication (before each sweep), which is not part of the local kernel.) |
Definition at line 4844 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::reorderedLocalGaussSeidel | ( | const MultiVector< DomainScalar, LocalOrdinal, GlobalOrdinal, node_type > & | B, |
| MultiVector< RangeScalar, LocalOrdinal, GlobalOrdinal, node_type > & | X, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | D, | ||
| const ArrayView< LocalOrdinal > & | rowIndices, | ||
| const RangeScalar & | dampingFactor, | ||
| const KokkosClassic::ESweepDirection | direction | ||
| ) | const |
Reordered Gauss-Seidel or SOR on .
Apply a forward or backward sweep of reordered Gauss-Seidel or Successive Over-Relaxation (SOR) to the linear system(s) . For Gauss-Seidel, set the damping factor omega to 1. The ordering can be a partial one, in which case the Gauss-Seidel is only executed on a local subset of unknowns.
| DomainScalar | The type of entries in the input multivector X. This may differ from the type of entries in A or in B. |
| RangeScalar | The type of entries in the output multivector B. This may differ from the type of entries in A or in X. |
| B | [in] Right-hand side(s). |
| X | [in/out] On input: initial guess(es). On output: result multivector(s). |
| D | [in] Inverse of diagonal entries of the matrix A. |
| rowIndices | [in] Ordered list of indices on which to execute GS. |
| omega | [in] SOR damping factor. omega = 1 results in Gauss-Seidel. |
| direction | [in] Sweep direction: KokkosClassic::Forward or KokkosClassic::Backward. ("Symmetric" requires interprocess communication (before each sweep), which is not part of the local kernel.) |
Definition at line 4912 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::localSolve | ( | const MultiVector< RangeScalar, LocalOrdinal, GlobalOrdinal, node_type > & | Y, |
| MultiVector< DomainScalar, LocalOrdinal, GlobalOrdinal, node_type > & | X, | ||
| Teuchos::ETransp | trans | ||
| ) | const |
Solves a linear system when the underlying matrix is triangular.
X is required to be post-imported, i.e., described by the column map of the matrix. Y is required to be pre-exported, i.e., described by the row map of the matrix.
This method is templated on the scalar type of MultiVector objects, allowing this method to be applied to MultiVector objects of arbitrary type. However, it is recommended that solve() not be called directly; instead, use the CrsMatrixSolveOp, as it will handle the Import/Export operations required to apply a matrix with non-trivial communication needs.
Both X and Y are required to have constant stride. However, unlike multiply(), it is permissible for &X == &Y. No run-time checking will be performed in a non-debug build.
Definition at line 4987 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| RCP<CrsMatrix<T,LocalOrdinal,GlobalOrdinal,node_type> > Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::convert | ( | ) | const |
Returns another CrsMatrix with the same entries, but represented as a different scalar type.
|
virtual |
Compute a sparse matrix-MultiVector multiply.
This method computes Y := beta*Y + alpha*Op(A)*X, where Op(A) is either , 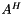(the transpose), or 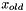(the conjugate transpose).
If beta == 0, this operation will enjoy overwrite semantics: Y's entries will be ignored, and Y will be overwritten with the result of the multiplication, even if it contains NaN (not-a-number) floating-point entries.
Definition at line 4096 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Whether apply() allows applying the transpose or conjugate transpose.
Reimplemented from Tpetra::Operator< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >.
Definition at line 535 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The domain Map of this operator.
This is null until fillComplete() has been called.
Definition at line 488 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The range Map of this operator.
This is null until fillComplete() has been called.
Definition at line 495 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::gaussSeidel | ( | const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | B, |
| MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | X, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | D, | ||
| const Scalar & | dampingFactor, | ||
| const ESweepDirection | direction, | ||
| const int | numSweeps | ||
| ) | const |
"Hybrid" Jacobi + (Gauss-Seidel or SOR) on .
"Hybrid" means Successive Over-Relaxation (SOR) or Gauss-Seidel within an (MPI) process, but Jacobi between processes. Gauss-Seidel is a special case of SOR, where the damping factor is one.
The Forward or Backward sweep directions have their usual SOR meaning within the process. Interprocess communication occurs once before the sweep, as it normally would in Jacobi.
The Symmetric sweep option means two sweeps: first Forward, then Backward. Interprocess communication occurs before each sweep, as in Jacobi. Thus, Symmetric results in two interprocess communication steps.
| B | [in] Right-hand side(s). |
| X | [in/out] On input: initial guess(es). On output: result multivector(s). |
| D | [in] Inverse of diagonal entries of the matrix A. |
| dampingFactor | [in] SOR damping factor. A damping factor of one results in Gauss-Seidel. |
| direction | [in] Sweep direction: Forward, Backward, or Symmetric. |
| numSweeps | [in] Number of sweeps. We count each Symmetric sweep (including both its Forward and its Backward sweep) as one. |
This method has the following requirements:
#1 is just the usual requirement for operators: the input multivector must always be in the domain Map. The Gauss-Seidel kernel imposes additional requirements, since it
#3 is reasonable if the matrix constructed the column Map, because the method that does this (CrsGraph::makeColMap) puts the local GIDs (those in the domain Map) in front and the remote GIDs (not in the domain Map) at the end of the column Map. However, if you constructed the column Map yourself, you are responsible for maintaining this invariant. #6 lets us do the Import from the domain Map to the column Map in place.
The Gauss-Seidel kernel also assumes that each process has the entire value (not a partial value to sum) of all the diagonal elements in the rows in its row Map. (We guarantee this anyway though the separate D vector.) This is because each element of the output multivector depends nonlinearly on the diagonal elements. Shared ownership of off-diagonal elements would produce different results.
Definition at line 4120 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::reorderedGaussSeidel | ( | const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | B, |
| MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | X, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | D, | ||
| const ArrayView< LocalOrdinal > & | rowIndices, | ||
| const Scalar & | dampingFactor, | ||
| const ESweepDirection | direction, | ||
| const int | numSweeps | ||
| ) | const |
Reordered "Hybrid" Jacobi + (Gauss-Seidel or SOR) on .
"Hybrid" means Successive Over-Relaxation (SOR) or Gauss-Seidel within an (MPI) process, but Jacobi between processes. Gauss-Seidel is a special case of SOR, where the damping factor is one. The ordering can be a partial one, in which case the Gauss-Seidel is only executed on a local subset of unknowns.
The Forward or Backward sweep directions have their usual SOR meaning within the process. Interprocess communication occurs once before the sweep, as it normally would in Jacobi.
The Symmetric sweep option means two sweeps: first Forward, then Backward. Interprocess communication occurs before each sweep, as in Jacobi. Thus, Symmetric results in two interprocess communication steps.
| B | [in] Right-hand side(s). |
| X | [in/out] On input: initial guess(es). On output: result multivector(s). |
| D | [in] Inverse of diagonal entries of the matrix A. |
| rowIndices | [in] Ordered list of indices on which to execute GS. |
| dampingFactor | [in] SOR damping factor. A damping factor of one results in Gauss-Seidel. |
| direction | [in] Sweep direction: Forward, Backward, or Symmetric. |
| numSweeps | [in] Number of sweeps. We count each Symmetric sweep (including both its Forward and its Backward sweep) as one. |
This method has the following requirements:
#1 is just the usual requirement for operators: the input multivector must always be in the domain Map. The Gauss-Seidel kernel imposes additional requirements, since it
#3 is reasonable if the matrix constructed the column Map, because the method that does this (CrsGraph::makeColMap) puts the local GIDs (those in the domain Map) in front and the remote GIDs (not in the domain Map) at the end of the column Map. However, if you constructed the column Map yourself, you are responsible for maintaining this invariant. #6 lets us do the Import from the domain Map to the column Map in place.
The Gauss-Seidel kernel also assumes that each process has the entire value (not a partial value to sum) of all the diagonal elements in the rows in its row Map. (We guarantee this anyway though the separate D vector.) This is because each element of the output multivector depends nonlinearly on the diagonal elements. Shared ownership of off-diagonal elements would produce different results.
Definition at line 4136 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::gaussSeidelCopy | ( | MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | X, |
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | B, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | D, | ||
| const Scalar & | dampingFactor, | ||
| const ESweepDirection | direction, | ||
| const int | numSweeps, | ||
| const bool | zeroInitialGuess | ||
| ) | const |
Version of gaussSeidel(), with fewer requirements on X.
This method is just like gaussSeidel(), except that X need only be in the domain Map. This method does not require that X be a domain Map view of a column Map multivector. As a result, this method must copy X into a domain Map multivector before operating on it.
| X | [in/out] On input: initial guess(es). On output: result multivector(s). |
| B | [in] Right-hand side(s), in the range Map. |
| D | [in] Inverse of diagonal entries of the matrix, in the row Map. |
| dampingFactor | [in] SOR damping factor. A damping factor of one results in Gauss-Seidel. |
| direction | [in] Sweep direction: Forward, Backward, or Symmetric. |
| numSweeps | [in] Number of sweeps. We count each Symmetric sweep (including both its Forward and its Backward sweep) as one. |
| zeroInitialGuess | [in] If true, this method will fill X with zeros initially. If false, this method will assume that X contains a possibly nonzero initial guess on input. Note that a nonzero initial guess may impose an additional nontrivial communication cost (an additional Import). |
Definition at line 4401 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::reorderedGaussSeidelCopy | ( | MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | X, |
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | B, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | D, | ||
| const ArrayView< LocalOrdinal > & | rowIndices, | ||
| const Scalar & | dampingFactor, | ||
| const ESweepDirection | direction, | ||
| const int | numSweeps, | ||
| const bool | zeroInitialGuess | ||
| ) | const |
Version of reorderedGaussSeidel(), with fewer requirements on X.
This method is just like reorderedGaussSeidel(), except that X need only be in the domain Map. This method does not require that X be a domain Map view of a column Map multivector. As a result, this method must copy X into a domain Map multivector before operating on it.
| X | [in/out] On input: initial guess(es). On output: result multivector(s). |
| B | [in] Right-hand side(s), in the range Map. |
| D | [in] Inverse of diagonal entries of the matrix, in the row Map. |
| rowIndices | [in] Ordered list of indices on which to execute GS. |
| dampingFactor | [in] SOR damping factor. A damping factor of one results in Gauss-Seidel. |
| direction | [in] Sweep direction: Forward, Backward, or Symmetric. |
| numSweeps | [in] Number of sweeps. We count each Symmetric sweep (including both its Forward and its Backward sweep) as one. |
| zeroInitialGuess | [in] If true, this method will fill X with zeros initially. If false, this method will assume that X contains a possibly nonzero initial guess on input. Note that a nonzero initial guess may impose an additional nontrivial communication cost (an additional Import). |
Definition at line 4418 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Implementation of RowMatrix::add: return alpha*A + beta*this.
This override of the default implementation ensures that, when called on a CrsMatrix, this method always returns a CrsMatrix of exactly the same type as *this. "Exactly the same
type" means that all the template parameters match, including the fifth template parameter. The input matrix A need not necessarily be a CrsMatrix or a CrsMatrix of the same type as *this, though this method may be able to optimize further in that case.
Reimplemented from Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >.
Definition at line 6288 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
A simple one-line description of this object.
Reimplemented from Tpetra::DistObject< char, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >.
Definition at line 5248 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Print the object with some verbosity level to an FancyOStream object.
Reimplemented from Tpetra::DistObject< char, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >.
Definition at line 5279 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Compare the source and target (this) objects for compatibility.
Definition at line 5513 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Perform copies and permutations that are local to this process.
| source | [in] On entry, the source object, from which we are distributing. We distribute to the destination object, which is *this object. |
| numSameIDs | [in] The umber of elements that are the same on the source and destination (this) objects. These elements are owned by the same process in both the source and destination objects. No permutation occurs. |
| numPermuteIDs | [in] The number of elements that are locally permuted between the source and destination objects. |
| permuteToLIDs | [in] List of the elements that are permuted. They are listed by their LID in the destination object. |
| permuteFromLIDs | [in] List of the elements that are permuted. They are listed by their LID in the source object. |
Definition at line 5537 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Perform any packing or preparation required for communication.
| source | [in] Source object for the redistribution. |
| exportLIDs | [in] List of the entries (as local IDs in the source object) we will be sending to other images. |
| exports | [out] On exit, the buffer for data to send. |
| numPacketsPerLID | [out] On exit, the implementation of this method must do one of two things: set numPacketsPerLID[i] to contain the number of packets to be exported for exportLIDs[i] and set constantNumPackets to zero, or set constantNumPackets to a nonzero value. If the latter, the implementation need not fill numPacketsPerLID. |
| constantNumPackets | [out] On exit, 0 if numPacketsPerLID has variable contents (different size for each LID). If nonzero, then it is expected that the number of packets per LID is constant, and that constantNumPackets is that value. |
| distor | [in] The Distributor object we are using. |
Definition at line 5695 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Unpack the imported column indices and values, and combine into matrix.
combineMode depends on whether the matrix's graph is static or dynamic. ADD, REPLACE, and ABSMAX are valid for a static graph, but INSERT is not. ADD and INSERT are valid for a dynamic graph; ABSMAX and REPLACE have not yet been implemented (and would require serious changes to matrix assembly in order to implement sensibly). Definition at line 6025 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Pack this object's data for an Import or Export.
Subclasses may override this method to speed up or otherwise improve the implementation by exploiting more specific details of the subclass.
Reimplemented from Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >.
Definition at line 5752 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
inline |
Get the Kokkos local values.
Definition at line 1995 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::importAndFillComplete | ( | Teuchos::RCP< CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, node_type > > & | destMatrix, |
| const import_type & | importer, | ||
| const Teuchos::RCP< const map_type > & | domainMap, | ||
| const Teuchos::RCP< const map_type > & | rangeMap, | ||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) | const |
Import from this to the given destination matrix, and make the result fill complete.
If destMatrix.is_null(), this creates a new matrix as the destination. (This is why destMatrix is passed in by nonconst reference to RCP.) Otherwise it checks for "pristine" status and throws if that is not the case. "Pristine" means that the matrix has no entries and is not fill complete.
Use of the "non-member constructor" version of this method, exportAndFillCompleteCrsMatrix, is preferred for user applications.
Definition at line 7047 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >::exportAndFillComplete | ( | Teuchos::RCP< CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, node_type > > & | destMatrix, |
| const export_type & | exporter, | ||
| const Teuchos::RCP< const map_type > & | domainMap = Teuchos::null, |
||
| const Teuchos::RCP< const map_type > & | rangeMap = Teuchos::null, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) | const |
Export from this to the given destination matrix, and make the result fill complete.
If destMatrix.is_null(), this creates a new matrix as the destination. (This is why destMatrix is passed in by nonconst reference to RCP.) Otherwise it checks for "pristine" status and throws if that is not the case. "Pristine" means that the matrix has no entries and is not fill complete.
Use of the "non-member constructor" version of this method, exportAndFillCompleteCrsMatrix, is preferred for user applications.
Definition at line 7065 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Allocate values (and optionally indices) using the Node.
| gas | [in] If GraphNotYetAllocated, allocate the indices of myGraph_ via allocateIndices(lg) before allocating values. |
| lg | [in] Argument passed into myGraph_->allocateIndices(), if applicable. |
Definition at line 567 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Sort the entries of each row by their column indices.
This only does anything if the graph isn't already sorted (i.e., ! myGraph_->isSorted ()). This method is called in fillComplete().
Definition at line 3764 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Merge entries in each row with the same column indices.
This only does anything if the graph isn't already merged (i.e., ! myGraph_->isMerged ()). This method is called in fillComplete().
Definition at line 3784 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Clear matrix properties that require collectives.
This clears whatever computeGlobalConstants() (which see) computed, in preparation for changes to the matrix. The current implementation of this method does nothing.
This method is called in resumeFill().
Definition at line 3526 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Compute matrix properties that require collectives.
The corresponding Epetra_CrsGraph method computes things like the global number of nonzero entries, that require collectives over the matrix's communicator. The current Tpetra implementation of this method does nothing.
This method is called in fillComplete().
Definition at line 3509 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Create a (or fetch a cached) column Map MultiVector.
| X_domainMap | [in] A domain Map Multivector. The returned MultiVector, if nonnull, will have the same number of columns as Y_domainMap. |
| force | [in] Force creating the MultiVector if it hasn't been created already. |
The force parameter is helpful when the domain Map and the column Map are the same (so that normally we wouldn't need the column Map MultiVector), but the following (for example) holds:
We don't test for the above in this method, because it depends on the specific kernel.
Definition at line 6140 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Create a (or fetch a cached) row Map MultiVector.
| Y_rangeMap | [in] A range Map Multivector. The returned MultiVector, if nonnull, will have the same number of columns as Y_rangeMap. |
| force | [in] Force creating the MultiVector if it hasn't been created already. |
The force parameter is helpful when the range Map and the row Map are the same (so that normally we wouldn't need the row Map MultiVector), but one of the following holds:
We don't test for the above in this method, because it depends on the specific kernel.
Definition at line 6204 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Special case of apply() for mode == Teuchos::NO_TRANS.
Definition at line 3806 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Special case of apply() for mode != Teuchos::NO_TRANS.
Definition at line 3970 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Constant view of all entries (including extra space) in the given row.
Definition at line 2279 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Nonconst view of all entries (including extra space) in the given row.
Definition at line 2311 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Fill data into the local matrix.
This method is only called in fillComplete(), and it is only called if the graph's structure is already fixed (that is, if the matrix does not own the graph).
Definition at line 1140 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Fill data into the local graph and matrix.
This method is only called in fillComplete(), and it is only called if the graph's structure is not already fixed (that is, if the matrix does own the graph).
Definition at line 677 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Check that this object's state is sane; throw if it's not.
Definition at line 5184 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
inherited |
Import data into this object using an Import object ("forward mode").
The input DistObject is always the source of the data redistribution operation, and the *this object is always the target.
If you don't know the difference between forward and reverse mode, then you probably want forward mode. Use this method with your precomputed Import object if you want to do an Import, else use doExport() with a precomputed Export object.
| source | [in] The "source" object for redistribution. |
| importer | [in] Precomputed data redistribution plan. Its source Map must be the same as the input DistObject's Map, and its target Map must be the same as this->getMap(). |
| CM | [in] How to combine incoming data with the same global index. |
|
inherited |
Import data into this object using an Export object ("reverse mode").
The input DistObject is always the source of the data redistribution operation, and the *this object is always the target.
If you don't know the difference between forward and reverse mode, then you probably want forward mode. Use the version of doImport() that takes a precomputed Import object in that case.
| source | [in] The "source" object for redistribution. |
| exporter | [in] Precomputed data redistribution plan. Its target Map must be the same as the input DistObject's Map, and its source Map must be the same as this->getMap(). (Note the difference from forward mode.) |
| CM | [in] How to combine incoming data with the same global index. |
|
inherited |
Export data into this object using an Export object ("forward mode").
The input DistObject is always the source of the data redistribution operation, and the *this object is always the target.
If you don't know the difference between forward and reverse mode, then you probably want forward mode. Use this method with your precomputed Export object if you want to do an Export, else use doImport() with a precomputed Import object.
| source | [in] The "source" object for redistribution. |
| exporter | [in] Precomputed data redistribution plan. Its source Map must be the same as the input DistObject's Map, and its target Map must be the same as this->getMap(). |
| CM | [in] How to combine incoming data with the same global index. |
|
inherited |
Export data into this object using an Import object ("reverse mode").
The input DistObject is always the source of the data redistribution operation, and the *this object is always the target.
If you don't know the difference between forward and reverse mode, then you probably want forward mode. Use the version of doExport() that takes a precomputed Export object in that case.
| source | [in] The "source" object for redistribution. |
| importer | [in] Precomputed data redistribution plan. Its target Map must be the same as the input DistObject's Map, and its source Map must be the same as this->getMap(). (Note the difference from forward mode.) |
| CM | [in] How to combine incoming data with the same global index. |
|
inherited |
Whether this is a globally distributed object.
For a definition of "globally distributed" (and its opposite, "locally replicated"), see the documentation of Map's isDistributed() method.
|
inlinevirtualinherited |
The Map describing the parallel distribution of this object.
Note that some Tpetra objects might be distributed using multiple Map objects. For example, CrsMatrix has both a row Map and a column Map. It is up to the subclass to decide which Map to use when invoking the DistObject constructor.
Definition at line 316 of file Tpetra_DistObject_decl.hpp.
|
inherited |
Print this object to the given output stream.
We generally assume that all MPI processes can print to the given stream.
|
virtualinherited |
Remove processes which contain no elements in this object's Map.
On input, this object is distributed over the Map returned by getMap() (the "original Map," with its communicator, the "original communicator"). The input newMap of this method must be the same as the result of calling getMap()->removeEmptyProcesses(). On processes in the original communicator which contain zero elements ("excluded processes," as opposed to "included processes"), the input newMap must be Teuchos::null (which is what getMap()->removeEmptyProcesses() returns anyway).
On included processes, reassign this object's Map (that would be returned by getMap()) to the input newMap, and do any work that needs to be done to restore correct semantics. On excluded processes, free any data that needs freeing, and do any other work that needs to be done to restore correct semantics.
This method has collective semantics over the original communicator. On exit, the only method of this object which is safe to call on excluded processes is the destructor. This implies that subclasses' destructors must not contain communication operations.
|
protectedvirtualinherited |
Whether the implementation's instance promises always to have a constant number of packets per LID, and if so, how many packets per LID there are.
If this method returns zero, the instance says that it might possibly have a different number of packets for each LID to send or receive. If it returns nonzero, the instance promises that the number of packets is the same for all LIDs, and that the return value is this number of packets per LID.
The default implementation of this method returns zero. This does not affect the behavior of doTransfer() in any way. If a nondefault implementation returns nonzero, doTransfer() will use this information to avoid unnecessary allocation and / or resizing of arrays.
|
protectedvirtualinherited |
Redistribute data across memory images.
| src | [in] The source object, to redistribute into the target object, which is *this object. |
| CM | [in] The combine mode that describes how to combine values that map to the same global ID on the same process. |
| permuteToLIDs | [in] See copyAndPermute(). |
| permuteFromLIDs | [in] See copyAndPermute(). |
| remoteLIDs | [in] List of entries (as local IDs) in the destination object to receive from other processes. |
| exportLIDs | [in] See packAndPrepare(). |
| distor | [in/out] The Distributor object that knows how to redistribute data. |
| revOp | [in] Whether to do a forward or reverse mode redistribution. |
|
protectedvirtualinherited |
Hook for creating a const view.
doTransfer() calls this on the source object. By default, it does nothing, but the source object can use this as a hint to fetch data from a compute buffer on an off-CPU device (such as a GPU) into host memory.
|
protectedvirtualinherited |
Hook for creating a nonconst view.
doTransfer() calls this on the destination (*this) object. By default, it does nothing, but the destination object can use this as a hint to fetch data from a compute buffer on an off-CPU device (such as a GPU) into host memory.
| rwo | [in] Whether to create a write-only or a read-and-write view. For Kokkos Node types where compute buffers live in a separate memory space (e.g., in the device memory of a discrete accelerator like a GPU), a write-only view only requires copying from host memory to the compute buffer, whereas a read-and-write view requires copying both ways (once to read, from the compute buffer to host memory, and once to write, back to the compute buffer). |
|
protectedvirtualinherited |
Hook for releasing views.
doTransfer() calls this on both the source and destination objects, once it no longer needs to access that object's data. By default, this method does nothing. Implementations may use this as a hint to free host memory which is a view of a compute buffer, once the host memory view is no longer needed. Some implementations may prefer to mirror compute buffers in host memory; for these implementations, releaseViews() may do nothing.
|
friend |
Nonmember CrsMatrix constructor that fuses Import and fillComplete().
| CrsMatrixType | A specialization of CrsMatrix. |
A common use case is to create an empty destination CrsMatrix, redistribute from a source CrsMatrix (by an Import or Export operation), then call fillComplete() on the destination CrsMatrix. This constructor fuses these three cases, for an Import redistribution.
Fusing redistribution and fillComplete() exposes potential optimizations. For example, it may make constructing the column Map faster, and it may avoid intermediate unoptimized storage in the destination CrsMatrix. These optimizations may improve performance for specialized kernels like sparse matrix-matrix multiply, as well as for redistributing data after doing load balancing.
The resulting matrix is fill complete (in the sense of isFillComplete()) and has optimized storage (in the sense of isStorageOptimized()). By default, its domain Map is the domain Map of the source matrix, and its range Map is the range Map of the source matrix.
| sourceMatrix | [in] The source matrix from which to import. The source of an Import must have a nonoverlapping distribution. |
| importer | [in] The Import instance containing a precomputed redistribution plan. The source Map of the Import must be the same as the rowMap of sourceMatrix unless the "Reverse Mode" option on the params list, in which case the targetMap of Import must match the rowMap of the sourceMatrix |
| domainMap | [in] Domain Map of the returned matrix. If null, we use the default, which is the domain Map of the source matrix. |
| rangeMap | [in] Range Map of the returned matrix. If null, we use the default, which is the range Map of the source matrix. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 2636 of file Tpetra_CrsMatrix_decl.hpp.
|
friend |
Nonmember CrsMatrix constructor that fuses Export and fillComplete().
| CrsMatrixType | A specialization of CrsMatrix. |
For justification, see the documentation of importAndFillCompleteCrsMatrix() (which is the Import analog of this function).
The resulting matrix is fill complete (in the sense of isFillComplete()) and has optimized storage (in the sense of isStorageOptimized()). By default, its domain Map is the domain Map of the source matrix, and its range Map is the range Map of the source matrix.
| sourceMatrix | [in] The source matrix from which to export. Its row Map may be overlapping, since the source of an Export may be overlapping. |
| exporter | [in] The Export instance containing a precomputed redistribution plan. The source Map of the Export must be the same as the row Map of sourceMatrix. |
| domainMap | [in] Domain Map of the returned matrix. If null, we use the default, which is the domain Map of the source matrix. |
| rangeMap | [in] Range Map of the returned matrix. If null, we use the default, which is the range Map of the source matrix. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 2688 of file Tpetra_CrsMatrix_decl.hpp.
|
mutableprotected |
Column Map MultiVector used in apply() and gaussSeidel().
This is a column Map MultiVector. It is used as the target of the forward mode Import operation (if necessary) in apply() and gaussSeidel(), and the source of the reverse mode Export operation (if necessary) in these methods. Both of these methods create this MultiVector on demand if needed, and reuse it (if possible) for subsequent calls.
This is declared mutable because the methods in question are const, yet want to cache the MultiVector for later use.
Definition at line 2330 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
mutableprotected |
Row Map MultiVector used in apply().
This is a row Map MultiVector. It is uses as the source of the forward mode Export operation (if necessary) in apply() and gaussSeidel(), and the target of the reverse mode Import operation (if necessary) in these methods. Both of these methods create this MultiVector on demand if needed, and reuse it (if possible) for subsequent calls.
This is declared mutable because the methods in question are const, yet want to cache the MultiVector for later use.
Definition at line 2344 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
protected |
The local sparse matrix.
Definition at line 2453 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
protected |
Status of the matrix's storage, when not in a fill-complete state.
The phrase "When not in a fill-complete state" is important. When the matrix is fill complete, it always uses 1-D "packed" storage. However, if the "Optimize Storage" parameter to fillComplete was false, the matrix may keep unpacked 1-D or 2-D storage around and resume it on the next resumeFill call.
Definition at line 2482 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
protected |
Whether the matrix is fill complete.
Definition at line 2485 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
protected |
Nonlocal data added using insertGlobalValues().
These data are cleared by globalAssemble(), once it finishes redistributing them to their owning processes.
For a given nonowned global row gRow which was given to insertGlobalValues() or sumIntoGlobalValues(), nonlocals_[gRow].first[k] is the column index of an inserted entry, and nonlocals_[gRow].second[k] is its value. Duplicate column indices for the same row index are allowed and will be summed during globalAssemble().
This used to be a map from GlobalOrdinal to (GlobalOrdinal, Scalar) pairs. This makes gcc issue a "note" about the ABI of structs containing std::complex members changing. CDash reports this as a warning, even though it's a "note," not a warning. However, I don't want it to show up, so I rearranged the map's value type to a pair of arrays, rather than an array of pairs.
Definition at line 2515 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
mutableprotected |
Cached Frobenius norm of the (global) matrix.
The value -1 (in general, -Teuchos::ScalarTraits<Magnitude>::one()) means that the norm has not yet been computed, or that the values in the matrix may have changed and the norm must be recomputed.
Definition at line 2523 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
protectedinherited |
The Map over which this object is distributed.
Definition at line 611 of file Tpetra_DistObject_decl.hpp.
|
protectedinherited |
Buffer into which packed data are imported (received from other processes).
Definition at line 615 of file Tpetra_DistObject_decl.hpp.
|
protectedinherited |
Number of packets to receive for each receive operation.
This array is used in Distributor::doPosts() (and doReversePosts()) when starting the ireceive operation.
This may be ignored in doTransfer() if constantNumPackets is nonzero, indicating a constant number of packets per LID. (For example, MultiVector sets the constantNumPackets output argument of packAndPrepare() to the number of columns in the multivector.)
Definition at line 627 of file Tpetra_DistObject_decl.hpp.
|
protectedinherited |
Buffer from which packed data are exported (sent to other processes).
Definition at line 630 of file Tpetra_DistObject_decl.hpp.
|
protectedinherited |
Number of packets to send for each send operation.
This array is used in Distributor::doPosts() (and doReversePosts()) for preparing for the send operation.
This may be ignored in doTransfer() if constantNumPackets is nonzero, indicating a constant number of packets per LID. (For example, MultiVector sets the constantNumPackets output argument of packAndPrepare() to the number of columns in the multivector.)
Definition at line 642 of file Tpetra_DistObject_decl.hpp.
1.8.6