Matrix subclass for variable reduction orthogonal matrix R = Gc(:,con_decomp)'*Y.
More...
|
| enum | EMatNormType { MAT_NORM_INF,
MAT_NORM_2,
MAT_NORM_1,
MAT_NORM_FORB
} |
| | Type of matrix norm. More...
|
| |
| MatrixOpNonsing & | operator= (const MatrixOpNonsing &M) |
| | Calls operator=(MatrixOp&) More...
|
| |
| virtual mat_mwons_mut_ptr_t | clone_mwons () |
| | Clone the non-const matrix object (if supported). More...
|
| |
| virtual mat_mwons_ptr_t | clone_mwons () const |
| | Clone the const matrix object (if supported). More...
|
| |
| const MatNorm | calc_cond_num (EMatNormType requested_norm_type=MAT_NORM_1, bool allow_replacement=false) const |
| | Compute an estimate of the condition number of this matrix. More...
|
| |
| mat_mut_ptr_t | clone () |
| | Returns this->clone_mwons(). More...
|
| |
| mat_ptr_t | clone () const |
| | Returns this->clone_mwons(). More...
|
| |
| mat_mns_mut_ptr_t | clone_mns () |
| | Returns this->clone_mwons(). More...
|
| |
| mat_mns_ptr_t | clone_mns () const |
| | Returns this->clone_mwons(). More...
|
| |
| virtual void | zero_out () |
| | M_lhs = 0 : Zero out the matrix. More...
|
| |
| virtual void | Mt_S (value_type alpha) |
| | M_lhs *= alpha : Multiply a matrix by a scalar. More...
|
| |
| virtual MatrixOp & | operator= (const MatrixOp &mwo_rhs) |
| | M_lhs = mwo_rhs : Virtual assignment operator. More...
|
| |
| const MatNorm | calc_norm (EMatNormType requested_norm_type=MAT_NORM_1, bool allow_replacement=false) const |
| | Compute a norm of this matrix. More...
|
| |
| virtual mat_ptr_t | sub_view (const Range1D &row_rng, const Range1D &col_rng) const |
| | Create a transient constant sub-matrix view of this matrix (if supported). More...
|
| |
| mat_ptr_t | sub_view (const index_type &rl, const index_type &ru, const index_type &cl, const index_type &cu) const |
| | Inlined implementation calls this->sub_view(Range1D(rl,ru),Range1D(cl,cu)). More...
|
| |
| virtual mat_ptr_t | perm_view (const Permutation *P_row, const index_type row_part[], int num_row_part, const Permutation *P_col, const index_type col_part[], int num_col_part) const |
| | Create a permuted view: M_perm = P_row' * M * P_col. More...
|
| |
| virtual mat_ptr_t | perm_view_update (const Permutation *P_row, const index_type row_part[], int num_row_part, const Permutation *P_col, const index_type col_part[], int num_col_part, const mat_ptr_t &perm_view) const |
| | Reinitialize a permuted view: M_perm = P_row' * M * P_col. More...
|
| |
| virtual | ~MatrixBase () |
| | Virtual destructor. More...
|
| |
| virtual size_type | nz () const |
| | Return the number of nonzero elements in the matrix. More...
|
| |
| virtual void | V_InvMtV (VectorMutable *v_lhs, BLAS_Cpp::Transp trans_rhs1, const Vector &v_rhs2) const =0 |
| | v_lhs = inv(op(M_rhs1)) * vs_rhs2 More...
|
| |
| virtual void | V_InvMtV (VectorMutable *v_lhs, BLAS_Cpp::Transp trans_rhs1, const SpVectorSlice &sv_rhs2) const |
| | v_lhs = inv(op(M_rhs1)) * sv_rhs2 More...
|
| |
| virtual value_type | transVtInvMtV (const Vector &v_rhs1, BLAS_Cpp::Transp trans_rhs2, const Vector &v_rhs3) const |
| | result = vs_rhs1' * inv(op(M_rhs2)) * vs_rhs3 More...
|
| |
| virtual value_type | transVtInvMtV (const SpVectorSlice &sv_rhs1, BLAS_Cpp::Transp trans_rhs2, const SpVectorSlice &sv_rhs3) const |
| | result = sv_rhs1' * inv(op(M_rhs2)) * sv_rhs3 More...
|
| |
| virtual void | M_StInvMtM (MatrixOp *m_lhs, value_type alpha, BLAS_Cpp::Transp trans_rhs1, const MatrixOp &mwo_rhs2, BLAS_Cpp::Transp trans_rhs2) const |
| | m_lhs = alpha * inv(op(M_rhs1)) * op(mwo_rhs2) (right). More...
|
| |
| virtual void | M_StMtInvM (MatrixOp *m_lhs, value_type alpha, const MatrixOp &mwo_rhs1, BLAS_Cpp::Transp trans_rhs1, BLAS_Cpp::Transp trans_rhs2) const |
| | m_lhs = alpha * op(mwo_rhs1) * inv(op(M_rhs2)) (left). More...
|
| |
| virtual bool | Mp_StM (MatrixOp *mwo_lhs, value_type alpha, BLAS_Cpp::Transp trans_rhs) const |
| | mwo_lhs += alpha * op(M_rhs) (BLAS xAXPY). More...
|
| |
| virtual bool | Mp_StM (value_type alpha, const MatrixOp &M_rhs, BLAS_Cpp::Transp trans_rhs) |
| | M_lhs += alpha * op(mwo_rhs) (BLAS xAXPY). More...
|
| |
| virtual bool | Mp_StMtP (MatrixOp *mwo_lhs, value_type alpha, BLAS_Cpp::Transp M_trans, const GenPermMatrixSlice &P_rhs, BLAS_Cpp::Transp P_rhs_trans) const |
| | mwo_lhs += alpha * op(M_rhs) * op(P_rhs). More...
|
| |
| virtual bool | Mp_StMtP (value_type alpha, const MatrixOp &mwo_rhs, BLAS_Cpp::Transp M_trans, const GenPermMatrixSlice &P_rhs, BLAS_Cpp::Transp P_rhs_trans) |
| | M_lhs += alpha * op(mwo_rhs) * op(P_rhs). More...
|
| |
| virtual bool | Mp_StPtM (MatrixOp *mwo_lhs, value_type alpha, const GenPermMatrixSlice &P_rhs, BLAS_Cpp::Transp P_rhs_trans, BLAS_Cpp::Transp M_trans) const |
| | mwo_lhs += alpha * op(P_rhs) * op(M_rhs). More...
|
| |
| virtual bool | Mp_StPtM (value_type alpha, const GenPermMatrixSlice &P_rhs, BLAS_Cpp::Transp P_rhs_trans, const MatrixOp &mwo_rhs, BLAS_Cpp::Transp M_trans) |
| | M_lhs += alpha * op(P_rhs) * op(mwo_rhs). More...
|
| |
| virtual bool | Mp_StPtMtP (MatrixOp *mwo_lhs, value_type alpha, const GenPermMatrixSlice &P_rhs1, BLAS_Cpp::Transp P_rhs1_trans, BLAS_Cpp::Transp M_trans, const GenPermMatrixSlice &P_rhs2, BLAS_Cpp::Transp P_rhs2_trans) const |
| | mwo_lhs += alpha * op(P_rhs1) * op(M_rhs) * op(P_rhs2). More...
|
| |
| virtual bool | Mp_StPtMtP (value_type alpha, const GenPermMatrixSlice &P_rhs1, BLAS_Cpp::Transp P_rhs1_trans, const MatrixOp &mwo_rhs, BLAS_Cpp::Transp M_trans, const GenPermMatrixSlice &P_rhs2, BLAS_Cpp::Transp P_rhs2_trans) |
| | M_lhs += alpha * op(P_rhs1) * op(mwo_rhs) * op(P_rhs2). More...
|
| |
| virtual void | Vp_StMtV (VectorMutable *v_lhs, value_type alpha, BLAS_Cpp::Transp trans_rhs1, const Vector &v_rhs2, value_type beta) const =0 |
| | v_lhs = alpha * op(M_rhs1) * v_rhs2 + beta * v_lhs (BLAS xGEMV) More...
|
| |
| virtual void | Vp_StMtV (VectorMutable *v_lhs, value_type alpha, BLAS_Cpp::Transp trans_rhs1, const SpVectorSlice &sv_rhs2, value_type beta) const |
| | v_lhs = alpha * op(M_rhs1) * sv_rhs2 + beta * v_lhs (BLAS xGEMV) More...
|
| |
| virtual void | Vp_StPtMtV (VectorMutable *v_lhs, value_type alpha, const GenPermMatrixSlice &P_rhs1, BLAS_Cpp::Transp P_rhs1_trans, BLAS_Cpp::Transp M_rhs2_trans, const Vector &v_rhs3, value_type beta) const |
| | v_lhs = alpha * op(P_rhs1) * op(M_rhs2) * v_rhs3 + beta * v_rhs More...
|
| |
| virtual void | Vp_StPtMtV (VectorMutable *v_lhs, value_type alpha, const GenPermMatrixSlice &P_rhs1, BLAS_Cpp::Transp P_rhs1_trans, BLAS_Cpp::Transp M_rhs2_trans, const SpVectorSlice &sv_rhs3, value_type beta) const |
| | v_lhs = alpha * op(P_rhs1) * op(M_rhs2) * sv_rhs3 + beta * v_rhs More...
|
| |
| virtual value_type | transVtMtV (const Vector &v_rhs1, BLAS_Cpp::Transp trans_rhs2, const Vector &v_rhs3) const |
| | result = v_rhs1' * op(M_rhs2) * v_rhs3 More...
|
| |
| virtual value_type | transVtMtV (const SpVectorSlice &sv_rhs1, BLAS_Cpp::Transp trans_rhs2, const SpVectorSlice &sv_rhs3) const |
| | result = sv_rhs1' * op(M_rhs2) * sv_rhs3 More...
|
| |
| virtual void | syr2k (BLAS_Cpp::Transp M_trans, value_type alpha, const GenPermMatrixSlice &P1, BLAS_Cpp::Transp P1_trans, const GenPermMatrixSlice &P2, BLAS_Cpp::Transp P2_trans, value_type beta, MatrixSymOp *symwo_lhs) const |
| | Perform a specialized rank-2k update of a dense symmetric matrix of the form: More...
|
| |
| virtual bool | Mp_StMtM (MatrixOp *mwo_lhs, value_type alpha, BLAS_Cpp::Transp trans_rhs1, const MatrixOp &mwo_rhs2, BLAS_Cpp::Transp trans_rhs2, value_type beta) const |
| | mwo_lhs = alpha * op(M_rhs1) * op(mwo_rhs2) + beta * mwo_lhs (left) (xGEMM). More...
|
| |
| virtual bool | Mp_StMtM (MatrixOp *mwo_lhs, value_type alpha, const MatrixOp &mwo_rhs1, BLAS_Cpp::Transp trans_rhs1, BLAS_Cpp::Transp trans_rhs2, value_type beta) const |
| | mwo_lhs = alpha * op(mwo_rhs1) * op(M_rhs2) + beta * mwo_lhs (right) (xGEMM) More...
|
| |
| virtual bool | Mp_StMtM (value_type alpha, const MatrixOp &mwo_rhs1, BLAS_Cpp::Transp trans_rhs1, const MatrixOp &mwo_rhs2, BLAS_Cpp::Transp trans_rhs2, value_type beta) |
| | M_lhs = alpha * op(mwo_rhs1) * op(mwo_rhs2) + beta * mwo_lhs (left) (xGEMM) More...
|
| |
| virtual bool | syrk (BLAS_Cpp::Transp M_trans, value_type alpha, value_type beta, MatrixSymOp *sym_lhs) const |
| | Perform a rank-k update of a symmetric matrix of the form: More...
|
| |
| virtual bool | syrk (const MatrixOp &mwo_rhs, BLAS_Cpp::Transp M_trans, value_type alpha, value_type beta) |
| | Perform a rank-k update of a symmetric matrix of the form: More...
|
| |
Matrix subclass for variable reduction orthogonal matrix R = Gc(:,con_decomp)'*Y.
This matrix class is used to represent the matrix:
R = C*(I + D*D')
inv(R) = inv(I + D*D') * inv(C)
= (I - D * inv(I + D'*D) * D') * inv(C)
\______/
S
Above, the expresion for inv(R) is derived using the Sherman-Morrison-Woodbury formula. The nonsingular matrix S = I + D'*D is setup by the client, along with the basis matrix C and the direct sensitivity matrix D.
Definition at line 67 of file ConstrainedOptPack_MatrixDecompRangeOrthog.hpp.
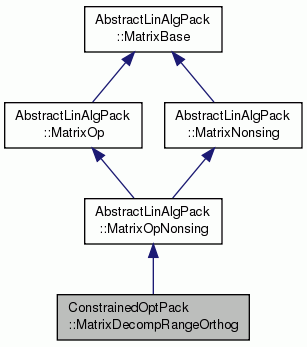
 Public Types inherited from AbstractLinAlgPack::MatrixOp
Public Types inherited from AbstractLinAlgPack::MatrixOp Public Member Functions inherited from AbstractLinAlgPack::MatrixOpNonsing
Public Member Functions inherited from AbstractLinAlgPack::MatrixOpNonsing Public Member Functions inherited from AbstractLinAlgPack::MatrixOp
Public Member Functions inherited from AbstractLinAlgPack::MatrixOp Public Member Functions inherited from AbstractLinAlgPack::MatrixBase
Public Member Functions inherited from AbstractLinAlgPack::MatrixBase Public Member Functions inherited from AbstractLinAlgPack::MatrixNonsing
Public Member Functions inherited from AbstractLinAlgPack::MatrixNonsing Protected Member Functions inherited from AbstractLinAlgPack::MatrixOp
Protected Member Functions inherited from AbstractLinAlgPack::MatrixOp 1.8.6
1.8.6