Defines expert-level interfaces for the evaluation of functions and operators in physical space (supported for FE, FV, and FD methods) and FE reference space; in addition, provides several function transformation utilities. More...
#include <Intrepid2_FunctionSpaceTools.hpp>
Static Public Member Functions | |
| template<class Scalar > | |
| static TransformedBasisValues < Scalar, DeviceType > | getHGRADtransformGRAD (const Data< Scalar, DeviceType > &jacobianInverse, const BasisValues< Scalar, DeviceType > &refBasisGradValues) |
| Transformation of a gradient field in the H-grad space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D). The returned object contains the transformed gradient field, defined on cells in physical space and indexed by (C,F,P,D). The transformations are computed on entry access; algorithms such as sum factorization rely on having access to the reference-space basis values as well as the transformation operator; both are stored in the returned TransformedBasisValues object. More... | |
| template<class Scalar > | |
| static TransformedBasisValues < Scalar, DeviceType > | getHGRADtransformVALUE (const ordinal_type &numCells, const BasisValues< Scalar, DeviceType > &refBasisValues) |
| Transformation of a (scalar) value field in the H-grad space, defined at points on a reference cell, stored in the user-provided container input and indexed by (F,P), into the output container output, defined on cells in physical space and indexed by (C,F,P). This transformation is trivial, and the returned container is logically indexed by (C,F,P), but only contains (F,P) distinct data entries. More... | |
| template<class Scalar > | |
| static TransformedBasisValues < Scalar, DeviceType > | getHCURLtransformVALUE (const Data< Scalar, DeviceType > &jacobianInverse, const BasisValues< Scalar, DeviceType > &refBasisValues) |
| Transformation of a (vector) value field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D). More... | |
| template<class Scalar > | |
| static TransformedBasisValues < Scalar, DeviceType > | getHCURLtransformCURL (const Data< Scalar, DeviceType > &jacobianDividedByJacobianDet, const BasisValues< Scalar, DeviceType > &refBasisValues) |
| Transformation of a 3D curl field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D). More... | |
| template<class Scalar > | |
| static TransformedBasisValues < Scalar, DeviceType > | getHCURLtransformCURL2D (const Data< Scalar, DeviceType > &jacobianDetInverse, const BasisValues< Scalar, DeviceType > &refBasisValues) |
| Transformation of a 2D curl field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P). More... | |
| template<class Scalar > | |
| static TransformedBasisValues < Scalar, DeviceType > | getHDIVtransformVALUE (const Data< Scalar, DeviceType > &jacobianDividedByJacobianDet, const BasisValues< Scalar, DeviceType > &refBasisValues) |
| Transformation of a (vector) value field in the H-div space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D). More... | |
| template<class Scalar > | |
| static TransformedBasisValues < Scalar, DeviceType > | getHDIVtransformDIV (const Data< Scalar, DeviceType > &jacobianDetInverse, const BasisValues< Scalar, DeviceType > &refBasisDivValues) |
| Transformation of a divergence field in the H-div space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P). More... | |
| template<class Scalar > | |
| static TransformedBasisValues < Scalar, DeviceType > | getHVOLtransformVALUE (const Data< Scalar, DeviceType > &jacobianDetInverse, const BasisValues< Scalar, DeviceType > &refBasisValues) |
| Transformation of a (scalar) value field in the H-vol space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P). More... | |
| template<typename outputValueType , class... outputProperties, typename inputValueType , class... inputProperties> | |
| static void | HGRADtransformVALUE (Kokkos::DynRankView< outputValueType, outputProperties...> output, const Kokkos::DynRankView< inputValueType, inputProperties...> input) |
| Transformation of a (scalar) value field in the H-grad space, defined at points on a reference cell, stored in the user-provided container input and indexed by (F,P), into the output container output, defined on cells in physical space and indexed by (C,F,P). More... | |
| template<typename outputValueType , class... outputProperties, typename inputValueType , class... inputProperties> | |
| static void | mapHGradDataFromPhysToRef (Kokkos::DynRankView< outputValueType, outputProperties...> output, const Kokkos::DynRankView< inputValueType, inputProperties...> input) |
Transformation of a (scalar) data in the H-grad space, defined in physical space, stored in the user-provided container input and indexed by (C,P), into the output container output, defined on reference cells and indexed by (C,P). It computes 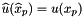 where where 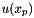 is the input H-grad data, is the input H-grad data, 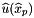 is the output H-grad data in the reference frame, and is the output H-grad data in the reference frame, and 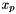 is the point in physical space corresponding to the the point is the point in physical space corresponding to the the point 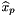 in the reference frame. Essentially this function copies the input into the output. More... in the reference frame. Essentially this function copies the input into the output. More... | |
| template<typename outputValueType , class... outputProperties, typename inputValueType , class... inputProperties> | |
| static void | mapHGradDataFromPhysSideToRefSide (Kokkos::DynRankView< outputValueType, outputProperties...> output, const Kokkos::DynRankView< inputValueType, inputProperties...> input) |
Transformation of a (scalar) data in the H-grad space, defined in physical space, stored in the user-provided container input and indexed by (C,P), into the output container output, defined on reference sides and indexed by (C,P). It computes 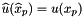 where where 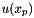 is the input H-grad data on physical sides, is the input H-grad data on physical sides, 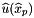 is the output H-grad data on the reference side, and is the output H-grad data on the reference side, and 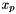 is the point on physical side corresponding to the the point is the point on physical side corresponding to the the point 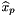 on the reference side. Essentially this function copies the input into the output. More... on the reference side. Essentially this function copies the input into the output. More... | |
| template<typename OutputValViewType , typename JacobianInverseViewType , typename InputValViewType > | |
| static void | HGRADtransformGRAD (OutputValViewType outputVals, const JacobianInverseViewType jacobianInverse, const InputValViewType inputVals) |
| Transformation of a gradient field in the H-grad space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D). More... | |
| template<typename outputValValueType , class... outputValProperties, typename jacobianInverseValueType , class... jacobianInverseProperties, typename inputValValueType , class... inputValProperties> | |
| static void | HCURLtransformVALUE (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< jacobianInverseValueType, jacobianInverseProperties...> jacobianInverse, const Kokkos::DynRankView< inputValValueType, inputValProperties...> inputVals) |
| Transformation of a (vector) value field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D). More... | |
| template<typename outputValValueType , class... outputValProperties, typename jacobianValueType , class... jacobianProperties, typename inputValValueType , class... inputValProperties> | |
| static void | mapHCurlDataFromPhysToRef (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< jacobianValueType, jacobianProperties...> jacobian, const Kokkos::DynRankView< inputValValueType, inputValProperties...> inputVals) |
| Transformation of a (vector) data in the H-curl space, defined in the physical space, stored in the user-provided container inputVals and indexed by (C,P,D), into the output container outputVals, defined on the reference cell and indexed by (C,P,D). More... | |
| template<typename outputValValueType , class... outputValProperties, typename tangentsValueType , class... tangentsProperties, typename metricTensorInvValueType , class... metricTensorInvProperties, typename metricTensorDetValueType , class... metricTensorDetProperties, typename inputValValueType , class... inputValProperties> | |
| static void | mapHCurlDataCrossNormalFromPhysSideToRefSide (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< tangentsValueType, tangentsProperties...> tangents, const Kokkos::DynRankView< metricTensorInvValueType, metricTensorInvProperties...> metricTensorInv, const Kokkos::DynRankView< metricTensorDetValueType, metricTensorDetProperties...> metricTensorDet, const Kokkos::DynRankView< inputValValueType, inputValProperties...> inputVals) |
Transformation of 3D HCURL data from physical side to reference side. It takes the input vector 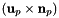 defined on physical sides and maps it into defined on physical sides and maps it into 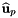 on the reference side. on the reference side. 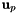 is a 3D HCURL function evaluated at points is a 3D HCURL function evaluated at points 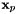 , , 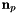 the outer unit normal to the sides at point the outer unit normal to the sides at point 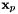 and and 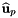 is a 2D HCURL function evaluated at reference points is a 2D HCURL function evaluated at reference points 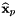 . More... . More... | |
| template<typename outputValValueType , class... outputValProperties, typename jacobianDetValueType , class... jacobianDetProperties, typename inputValValueType , class... inputValProperties> | |
| static void | mapHCurlDataCrossNormalFromPhysSideToRefSide (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< jacobianDetValueType, jacobianDetProperties...> metricTensorDet, const Kokkos::DynRankView< inputValValueType, inputValProperties...> inputVals) |
Transformation of 2D HCURL data from physical side to reference side. It takes the input scalar 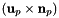 defined on physical sides and maps it into defined on physical sides and maps it into 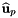 on the reference side. on the reference side. 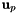 is a 2D HCURL function evaluated at points is a 2D HCURL function evaluated at points 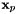 , , 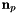 the unit outer normal to the sides at point the unit outer normal to the sides at point 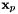 and and 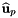 is a 2D HVOL function evaluated at reference points is a 2D HVOL function evaluated at reference points 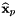 . Note, . Note, 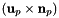 is computed by extending the 2D vectors (in xy plane) to the 3D space, and taking only the component of the cross product in the z-axis direction. More... is computed by extending the 2D vectors (in xy plane) to the 3D space, and taking only the component of the cross product in the z-axis direction. More... | |
| template<typename outputValValueType , class... outputValProperties, typename jacobianValueType , class... jacobianProperties, typename jacobianDetValueType , class... jacobianDetProperties, typename inputValValueType , class... inputValProperties> | |
| static void | HCURLtransformCURL (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< jacobianValueType, jacobianProperties...> jacobian, const Kokkos::DynRankView< jacobianDetValueType, jacobianDetProperties...> jacobianDet, const Kokkos::DynRankView< inputValValueType, inputValProperties...> inputVals) |
| Transformation of a 3D curl field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D). More... | |
| template<typename outputValValueType , class... outputValProperties, typename jacobianDetValueType , class... jacobianDetProperties, typename inputValValueType , class... inputValProperties> | |
| static void | HCURLtransformCURL (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< jacobianDetValueType, jacobianDetProperties...> jacobianDet, const Kokkos::DynRankView< inputValValueType, inputValProperties...> inputVals) |
| Transformation of a 2D curl field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P). More... | |
| template<typename outputValValueType , class... outputValProperties, typename jacobianValueType , class... jacobianProperties, typename jacobianDetValueType , class... jacobianDetProperties, typename inputValValueType , class... inputValProperties> | |
| static void | HGRADtransformCURL (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< jacobianValueType, jacobianProperties...> jacobian, const Kokkos::DynRankView< jacobianDetValueType, jacobianDetProperties...> jacobianDet, const Kokkos::DynRankView< inputValValueType, inputValProperties...> inputVals) |
| Transformation of a 2D curl field in the H-grad space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D). More... | |
| template<typename outputValValueType , class... outputValProperties, typename jacobianValueType , class... jacobianProperties, typename jacobianDetValueType , class... jacobianDetProperties, typename inputValValueType , class... inputValProperties> | |
| static void | HDIVtransformVALUE (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< jacobianValueType, jacobianProperties...> jacobian, const Kokkos::DynRankView< jacobianDetValueType, jacobianDetProperties...> jacobianDet, const Kokkos::DynRankView< inputValValueType, inputValProperties...> inputVals) |
| Transformation of a (vector) value field in the H-div space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D). More... | |
| template<typename outputValValueType , class... outputValProperties, typename jacobianInverseValueType , class... jacobianInverseProperties, typename jacobianDetValueType , class... jacobianDetProperties, typename inputValValueType , class... inputValProperties> | |
| static void | mapHDivDataFromPhysToRef (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< jacobianInverseValueType, jacobianInverseProperties...> jacobianInv, const Kokkos::DynRankView< jacobianDetValueType, jacobianDetProperties...> jacobianDet, const Kokkos::DynRankView< inputValValueType, inputValProperties...> inputVals) |
| Transformation of a (vector) data in the H-div space, defined in the physical space, stored in the user-provided container inputVals and indexed by (C,P,D), into the output container outputVals, defined on the reference cell and indexed by (C,P,D). More... | |
| template<typename outputValValueType , class... outputValProperties, typename jacobianDetValueType , class... jacobianDetProperties, typename inputValValueType , class... inputValProperties> | |
| static void | mapHDivDataDotNormalFromPhysSideToRefSide (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< jacobianDetValueType, jacobianDetProperties...> metricTensorDet, const Kokkos::DynRankView< inputValValueType, inputValProperties...> inputVals) |
Transformation of HDIV data from physical side to reference side. It takes the input 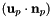 defined on physical sides and maps it into defined on physical sides and maps it into 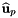 on the reference side. on the reference side. 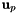 is a HDIV function evaluated at points is a HDIV function evaluated at points 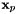 , , 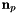 the outer unit normal to the sides at point the outer unit normal to the sides at point 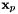 and and 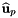 is a HVOL data evaluated at reference points is a HVOL data evaluated at reference points 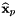 . More... . More... | |
| template<typename outputValValueType , class... outputValProperties, typename jacobianDetValueType , class... jacobianDetProperties, typename inputValValueType , class... inputValProperties> | |
| static void | HDIVtransformDIV (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< jacobianDetValueType, jacobianDetProperties...> jacobianDet, const Kokkos::DynRankView< inputValValueType, inputValProperties...> inputVals) |
| Transformation of a divergence field in the H-div space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P). More... | |
| template<typename outputValValueType , class... outputValProperties, typename jacobianDetValueType , class... jacobianDetProperties, typename inputValValueType , class... inputValProperties> | |
| static void | HVOLtransformVALUE (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< jacobianDetValueType, jacobianDetProperties...> jacobianDet, const Kokkos::DynRankView< inputValValueType, inputValProperties...> inputVals) |
| Transformation of a (scalar) value field in the H-vol space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P). More... | |
| template<typename outputValValueType , class... outputValProperties, typename jacobianDetValueType , class... jacobianDetProperties, typename inputValValueType , class... inputValProperties> | |
| static void | mapHVolDataFromPhysToRef (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< jacobianDetValueType, jacobianDetProperties...> jacobianDet, const Kokkos::DynRankView< inputValValueType, inputValProperties...> inputVals) |
| Transformation of a (scalar) data in the H-vol space, defined in the physical space, stored in the user-provided container inputVals and indexed by (C,P), into the output container outputVals, defined on the reference cell and indexed by (C,P). More... | |
| template<typename outputValueValueType , class... outputValueProperties, typename leftValueValueType , class... leftValueProperties, typename rightValueValueType , class... rightValueProperties> | |
| static void | integrate (Kokkos::DynRankView< outputValueValueType, outputValueProperties...> outputValues, const Kokkos::DynRankView< leftValueValueType, leftValueProperties...> leftValues, const Kokkos::DynRankView< rightValueValueType, rightValueProperties...> rightValues, const bool sumInto=false) |
| Contracts leftValues and rightValues arrays on the point and possibly space dimensions and stores the result in outputValues; this is a generic, high-level integration routine that calls either FunctionSpaceTools::operatorIntegral, or FunctionSpaceTools::functionalIntegral, or FunctionSpaceTools::dataIntegral methods, depending on the rank of the outputValues array. More... | |
| template<typename OutputValViewType , typename InputDetViewType , typename InputWeightViewType > | |
| static bool | computeCellMeasure (OutputValViewType outputVals, const InputDetViewType inputDet, const InputWeightViewType inputWeights) |
| Returns the weighted integration measures outputVals with dimensions (C,P) used for the computation of cell integrals, by multiplying absolute values of the user-provided cell Jacobian determinants inputDet with dimensions (C,P) with the user-provided integration weights inputWeights with dimensions (P). More... | |
| template<typename outputValValueType , class... outputValProperties, typename inputJacValueType , class... inputJacProperties, typename inputWeightValueType , class... inputWeightPropertes, typename scratchValueType , class... scratchProperties> | |
| static void | computeFaceMeasure (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< inputJacValueType, inputJacProperties...> inputJac, const Kokkos::DynRankView< inputWeightValueType, inputWeightPropertes...> inputWeights, const int whichFace, const shards::CellTopology parentCell, const Kokkos::DynRankView< scratchValueType, scratchProperties...> scratch) |
| Returns the weighted integration measures outputVals with dimensions (C,P) used for the computation of face integrals, based on the provided cell Jacobian array inputJac with dimensions (C,P,D,D) and the provided integration weights inputWeights with dimensions (P). More... | |
| template<typename outputValValueType , class... outputValProperties, typename inputJacValueType , class... inputJacProperties, typename inputWeightValueType , class... inputWeightProperties, typename scratchValueType , class... scratchProperties> | |
| static void | computeEdgeMeasure (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< inputJacValueType, inputJacProperties...> inputJac, const Kokkos::DynRankView< inputWeightValueType, inputWeightProperties...> inputWeights, const int whichEdge, const shards::CellTopology parentCell, const Kokkos::DynRankView< scratchValueType, scratchProperties...> scratch) |
| Returns the weighted integration measures outVals with dimensions (C,P) used for the computation of edge integrals, based on the provided cell Jacobian array inputJac with dimensions (C,P,D,D) and the provided integration weights inWeights with dimensions (P). More... | |
| template<typename outputValValueType , class... outputValProperties, typename inputMeasureValueType , class... inputMeasureProperties, typename inputValValueType , class... inputValProperteis> | |
| static void | multiplyMeasure (Kokkos::DynRankView< outputValValueType, outputValProperties...> outputVals, const Kokkos::DynRankView< inputMeasureValueType, inputMeasureProperties...> inputMeasure, const Kokkos::DynRankView< inputValValueType, inputValProperteis...> inputVals) |
| Multiplies fields inputVals by weighted measures inputMeasure and returns the field array outputVals; this is a simple redirection to the call FunctionSpaceTools::scalarMultiplyDataField. More... | |
| template<typename outputFieldValueType , class... outputFieldProperties, typename inputDataValueType , class... inputDataPropertes, typename inputFieldValueType , class... inputFieldProperties> | |
| static void | scalarMultiplyDataField (Kokkos::DynRankView< outputFieldValueType, outputFieldProperties...> outputFields, const Kokkos::DynRankView< inputDataValueType, inputDataPropertes...> inputData, const Kokkos::DynRankView< inputFieldValueType, inputFieldProperties...> inputFields, const bool reciprocal=false) |
| Scalar multiplication of data and fields; please read the description below. More... | |
| template<typename outputDataValuetype , class... outputDataProperties, typename inputDataLeftValueType , class... inputDataLeftProperties, typename inputDataRightValueType , class... inputDataRightProperties> | |
| static void | scalarMultiplyDataData (Kokkos::DynRankView< outputDataValuetype, outputDataProperties...> outputData, const Kokkos::DynRankView< inputDataLeftValueType, inputDataLeftProperties...> inputDataLeft, const Kokkos::DynRankView< inputDataRightValueType, inputDataRightProperties...> inputDataRight, const bool reciprocal=false) |
| Scalar multiplication of data and data; please read the description below. More... | |
| template<typename outputFieldValueType , class... outputFieldProperties, typename inputDataValueType , class... inputDataProperties, typename inputFieldValueType , class... inputFieldProperties> | |
| static void | dotMultiplyDataField (Kokkos::DynRankView< outputFieldValueType, outputFieldProperties...> outputFields, const Kokkos::DynRankView< inputDataValueType, inputDataProperties...> inputData, const Kokkos::DynRankView< inputFieldValueType, inputFieldProperties...> inputFields) |
| Dot product of data and fields; please read the description below. More... | |
| template<typename outputDataValueType , class... outputDataProperties, typename inputDataLeftValueType , class... inputDataLeftProperties, typename inputDataRightValueType , class... inputDataRightProperties> | |
| static void | dotMultiplyDataData (Kokkos::DynRankView< outputDataValueType, outputDataProperties...> outputData, const Kokkos::DynRankView< inputDataLeftValueType, inputDataLeftProperties...> inputDataLeft, const Kokkos::DynRankView< inputDataRightValueType, inputDataRightProperties...> inputDataRight) |
| Dot product of data and data; please read the description below. More... | |
| template<typename outputFieldValueType , class... outputFieldProperties, typename inputDataValueType , class... inputDataProperties, typename inputFieldValueType , class... inputFieldProperties> | |
| static void | vectorMultiplyDataField (Kokkos::DynRankView< outputFieldValueType, outputFieldProperties...> outputFields, const Kokkos::DynRankView< inputDataValueType, inputDataProperties...> inputData, const Kokkos::DynRankView< inputFieldValueType, inputFieldProperties...> inputFields) |
| Cross or outer product of data and fields; please read the description below. More... | |
| template<typename outputDataValueType , class... outputDataProperties, typename inputDataLeftValueType , class... inputDataLeftProperties, typename inputDataRightValueType , class... inputDataRightProperties> | |
| static void | vectorMultiplyDataData (Kokkos::DynRankView< outputDataValueType, outputDataProperties...> outputData, const Kokkos::DynRankView< inputDataLeftValueType, inputDataLeftProperties...> inputDataLeft, const Kokkos::DynRankView< inputDataRightValueType, inputDataRightProperties...> inputDataRight) |
| Cross or outer product of data and data; please read the description below. More... | |
| template<typename outputFieldValueType , class... outputFieldProperties, typename inputDataValueType , class... inputDataProperties, typename inputFieldValueType , class... inputFieldProperties> | |
| static void | tensorMultiplyDataField (Kokkos::DynRankView< outputFieldValueType, outputFieldProperties...> outputFields, const Kokkos::DynRankView< inputDataValueType, inputDataProperties...> inputData, const Kokkos::DynRankView< inputFieldValueType, inputFieldProperties...> inputFields, const char transpose= 'N') |
| Matrix-vector or matrix-matrix product of data and fields; please read the description below. More... | |
| template<typename outputDataValueType , class... outputDataProperties, typename inputDataLeftValueType , class... inputDataLeftProperties, typename inputDataRightValueType , class... inputDataRightProperties> | |
| static void | tensorMultiplyDataData (Kokkos::DynRankView< outputDataValueType, outputDataProperties...> outputData, const Kokkos::DynRankView< inputDataLeftValueType, inputDataLeftProperties...> inputDataLeft, const Kokkos::DynRankView< inputDataRightValueType, inputDataRightProperties...> inputDataRight, const char transpose= 'N') |
| Matrix-vector or matrix-matrix product of data and data; please read the description below. More... | |
| template<typename inoutOperatorValueType , class... inoutOperatorProperties, typename fieldSignValueType , class... fieldSignProperties> | |
| static void | applyLeftFieldSigns (Kokkos::DynRankView< inoutOperatorValueType, inoutOperatorProperties...> inoutOperator, const Kokkos::DynRankView< fieldSignValueType, fieldSignProperties...> fieldSigns) |
| Applies left (row) signs, stored in the user-provided container fieldSigns and indexed by (C,L), to the operator inoutOperator indexed by (C,L,R). More... | |
| template<typename inoutOperatorValueType , class... inoutOperatorProperties, typename fieldSignValueType , class... fieldSignProperties> | |
| static void | applyRightFieldSigns (Kokkos::DynRankView< inoutOperatorValueType, inoutOperatorProperties...> inoutOperator, const Kokkos::DynRankView< fieldSignValueType, fieldSignProperties...> fieldSigns) |
| Applies right (column) signs, stored in the user-provided container fieldSigns and indexed by (C,R), to the operator inoutOperator indexed by (C,L,R). More... | |
| template<typename inoutFunctionValueType , class... inoutFunctionProperties, typename fieldSignValueType , class... fieldSignProperties> | |
| static void | applyFieldSigns (Kokkos::DynRankView< inoutFunctionValueType, inoutFunctionProperties...> inoutFunction, const Kokkos::DynRankView< fieldSignValueType, fieldSignProperties...> fieldSigns) |
| Applies field signs, stored in the user-provided container fieldSigns and indexed by (C,F), to the function inoutFunction indexed by (C,F), (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2). More... | |
| template<typename outputPointValueType , class... outputPointProperties, typename inputCoeffValueType , class... inputCoeffProperties, typename inputFieldValueType , class... inputFieldProperties> | |
| static void | evaluate (Kokkos::DynRankView< outputPointValueType, outputPointProperties...> outputPointVals, const Kokkos::DynRankView< inputCoeffValueType, inputCoeffProperties...> inputCoeffs, const Kokkos::DynRankView< inputFieldValueType, inputFieldProperties...> inputFields) |
| Computes point values outPointVals of a discrete function specified by the basis inFields and coefficients inCoeffs. More... | |
Private Types | |
| using | ExecSpaceType = typename DeviceType::execution_space |
| using | MemSpaceType = typename DeviceType::memory_space |
Detailed Description
template<typename DeviceType>
class Intrepid2::FunctionSpaceTools< DeviceType >
Defines expert-level interfaces for the evaluation of functions and operators in physical space (supported for FE, FV, and FD methods) and FE reference space; in addition, provides several function transformation utilities.
Definition at line 49 of file Intrepid2_FunctionSpaceTools.hpp.
Member Function Documentation
|
static |
Applies field signs, stored in the user-provided container fieldSigns and indexed by (C,F), to the function inoutFunction indexed by (C,F), (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2).
Returns
![\[ \mbox{inoutFunction}(c,f,*) = \mbox{fieldSigns}(c,f)*\mbox{inoutFunction}(c,f,*) \]](form_228.png)
See Section Pullbacks for discussion of field signs.
- Parameters
-
inoutFunction [in/out] - Input / output function array. fieldSigns [in] - Right field signs.
Definition at line 1047 of file Intrepid2_FunctionSpaceToolsDef.hpp.
|
static |
Applies left (row) signs, stored in the user-provided container fieldSigns and indexed by (C,L), to the operator inoutOperator indexed by (C,L,R).
Mathematically, this method computes the matrix-matrix product
![\[ \mathbf{K}^{c} = \mbox{diag}(\sigma^c_0,\ldots,\sigma^c_{L-1}) \mathbf{K}^c \]](form_223.png)
where 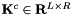 is array of matrices indexed by cell number c and stored in the rank-3 array inoutOperator, and
is array of matrices indexed by cell number c and stored in the rank-3 array inoutOperator, and 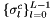 is array of left field signs indexed by cell number c and stored in the rank-2 container fieldSigns; see Section Pullbacks for discussion of field signs. This operation is required for operators generated by HCURL and HDIV-conforming vector-valued finite element basis functions; see Sections Pullbacks and Section Evaluation of finite element operators and functionals for applications of this method.
is array of left field signs indexed by cell number c and stored in the rank-2 container fieldSigns; see Section Pullbacks for discussion of field signs. This operation is required for operators generated by HCURL and HDIV-conforming vector-valued finite element basis functions; see Sections Pullbacks and Section Evaluation of finite element operators and functionals for applications of this method.
- Parameters
-
inoutOperator [in/out] - Input / output operator array. fieldSigns [in] - Left field signs.
Definition at line 917 of file Intrepid2_FunctionSpaceToolsDef.hpp.
|
static |
Applies right (column) signs, stored in the user-provided container fieldSigns and indexed by (C,R), to the operator inoutOperator indexed by (C,L,R).
Mathematically, this method computes the matrix-matrix product
![\[ \mathbf{K}^{c} = \mathbf{K}^c \mbox{diag}(\sigma^c_0,\ldots,\sigma^c_{R-1}) \]](form_226.png)
where 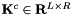 is array of matrices indexed by cell number c and stored in the rank-3 container inoutOperator, and
is array of matrices indexed by cell number c and stored in the rank-3 container inoutOperator, and 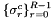 is array of right field signs indexed by cell number c and stored in the rank-2 container fieldSigns; see Section Pullbacks for discussion of field signs. This operation is required for operators generated by HCURL and HDIV-conforming vector-valued finite element basis functions; see Sections Pullbacks and Section Evaluation of finite element operators and functionals for applications of this method.
is array of right field signs indexed by cell number c and stored in the rank-2 container fieldSigns; see Section Pullbacks for discussion of field signs. This operation is required for operators generated by HCURL and HDIV-conforming vector-valued finite element basis functions; see Sections Pullbacks and Section Evaluation of finite element operators and functionals for applications of this method.
- Parameters
-
inoutOperator [in/out] - Input / output operator array. fieldSigns [in] - Right field signs.
Definition at line 980 of file Intrepid2_FunctionSpaceToolsDef.hpp.
|
static |
Returns the weighted integration measures outputVals with dimensions (C,P) used for the computation of cell integrals, by multiplying absolute values of the user-provided cell Jacobian determinants inputDet with dimensions (C,P) with the user-provided integration weights inputWeights with dimensions (P).
Returns a rank-2 array (C, P) array such that
![\[ \mbox{outputVals}(c,p) = |\mbox{det}(DF_{c}(\widehat{x}_p))|\omega_{p} \,, \]](form_212.png)
where 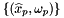 is a cubature rule defined on a reference cell (a set of integration points and their associated weights; see Intrepid2::Cubature::getCubature for getting cubature rules on reference cells).
is a cubature rule defined on a reference cell (a set of integration points and their associated weights; see Intrepid2::Cubature::getCubature for getting cubature rules on reference cells).
- Warning
- The user is responsible for providing input arrays with consistent data: the determinants in inputDet should be evaluated at integration points on the reference cell corresponding to the weights in inputWeights.
- Remarks
- See Intrepid2::CellTools::setJacobian for computation of DF and Intrepid2::CellTools::setJacobianDet for computation of its determinant.
- Parameters
-
outputVals [out] - Output array with weighted cell measures. inputDet [in] - Input array containing determinants of cell Jacobians. inputWeights [in] - Input integration weights.
Definition at line 537 of file Intrepid2_FunctionSpaceToolsDef.hpp.
|
static |
Returns the weighted integration measures outVals with dimensions (C,P) used for the computation of edge integrals, based on the provided cell Jacobian array inputJac with dimensions (C,P,D,D) and the provided integration weights inWeights with dimensions (P).
Returns a rank-2 array (C, P) array such that
![\[ \mbox{outVals}(c,p) = \left\|\frac{d \Phi_c(\widehat{x}_p)}{d s}\right\|\omega_{p} \,, \]](form_217.png)
where:
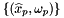 is a cubature rule defined on reference edge
is a cubature rule defined on reference edge 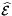 , with ordinal whichEdge relative to the specified parent reference cell;
, with ordinal whichEdge relative to the specified parent reference cell; 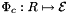 is parameterization of the physical edge corresponding to
is parameterization of the physical edge corresponding to 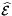 ; see Section Parametrization of physical 1- and 2-subcells.
; see Section Parametrization of physical 1- and 2-subcells.
- Warning
- The user is responsible for providing input arrays with consistent data: the Jacobians in inputJac should be evaluated at integration points on the reference edge corresponding to the weights in inputWeights. Additionally, the user is responsible for providing a scratch array of the same dimension as the inputJac array.
- Remarks
- Cubature rules on reference edges are defined by a two-step process:
- A cubature rule is defined on the parametrization domain R = [-1,1] of the edge.
- The points are mapped to a reference edge using Intrepid2::CellTools::mapToReferenceSubcell
- See Intrepid2::CellTools::setJacobian for computation of DF and Intrepid2::CellTools::setJacobianDet for computation of its determinant.
- Parameters
-
outputVals [out] - Output array with weighted edge measures. inputJac [in] - Input array containing cell Jacobians. inputWeights [in] - Input integration weights. whichEdge [in] - Index of the edge subcell relative to the parent cell; defines the domain of integration. parentCell [in] - Parent cell topology. scratch [in] - Scratch space, sized like inputJac
Definition at line 630 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::CellTools< DeviceType >::getPhysicalEdgeTangents(), Intrepid2::ArrayTools< DeviceType >::scalarMultiplyDataData(), and Intrepid2::RealSpaceTools< DeviceType >::vectorNorm().
Referenced by Intrepid2::CubatureControlVolumeBoundary< DeviceType, pointValueType, weightValueType >::getCubature().
|
static |
Returns the weighted integration measures outputVals with dimensions (C,P) used for the computation of face integrals, based on the provided cell Jacobian array inputJac with dimensions (C,P,D,D) and the provided integration weights inputWeights with dimensions (P).
Returns a rank-2 array (C, P) array such that
![\[ \mbox{outputVals}(c,p) = \left\|\frac{\partial\Phi_c(\widehat{x}_p)}{\partial u}\times \frac{\partial\Phi_c(\widehat{x}_p)}{\partial v}\right\|\omega_{p} \,, \]](form_214.png)
where:
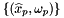 is a cubature rule defined on reference face
is a cubature rule defined on reference face 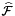 , with ordinal whichFace relative to the specified parent reference cell;
, with ordinal whichFace relative to the specified parent reference cell; 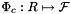 is parameterization of the physical face corresponding to
is parameterization of the physical face corresponding to 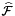 ; see Section Parametrization of physical 1- and 2-subcells.
; see Section Parametrization of physical 1- and 2-subcells.
- Warning
- The user is responsible for providing input arrays with consistent data: the Jacobians in inputJac should be evaluated at integration points on the reference face corresponding to the weights in inputWeights. Additionally, the user is responsible for providing a scratch array of the same dimension as the inputJac array.
- Remarks
- Cubature rules on reference faces are defined by a two-step process:
- A cubature rule is defined on the parametrization domain R of the face (R is the standard 2-simplex {(0,0),(1,0),(0,1)} or the standard 2-cube [-1,1] X [-1,1]).
- The points are mapped to a reference face using Intrepid2::CellTools::mapToReferenceSubcell
- See Intrepid2::CellTools::setJacobian for computation of DF and Intrepid2::CellTools::setJacobianDet for computation of its determinant.
- Parameters
-
outputVals [out] - Output array with weighted face measures. inputJac [in] - Input array containing cell Jacobians. inputWeights [in] - Input integration weights. whichFace [in] - Index of the face subcell relative to the parent cell; defines the domain of integration. parentCell [in] - Parent cell topology. scratch [in] - Scratch space, sized like inputJac
Definition at line 583 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::CellTools< DeviceType >::getPhysicalFaceNormals(), Intrepid2::ArrayTools< DeviceType >::scalarMultiplyDataData(), and Intrepid2::RealSpaceTools< DeviceType >::vectorNorm().
Referenced by Intrepid2::CubatureControlVolumeBoundary< DeviceType, pointValueType, weightValueType >::getCubature().
|
static |
Dot product of data and data; please read the description below.
There are two use cases:
- dot product of a rank-2, 3 or 4 container inputDataRight with dimensions (C,P) (C,P,D1) or (C,P,D1,D2), representing the values of a scalar, vector or a tensor set of data, by the values in a rank-2, 3 or 4 container inputDataLeft indexed by (C,P), (C,P,D1), or (C,P,D1,D2) representing the values of scalar, vector or tensor data, OR
- dot product of a rank-2, 3 or 4 container inputDataRight with dimensions (P), (P,D1) or (P,D1,D2), representing the values of scalar, vector or tensor data, by the values in a rank-2 container inputDataLeft indexed by (C,P), (C,P,D1) or (C,P,D1,D2), representing the values of scalar, vector, or tensor data; the output value container outputData is indexed by (C,P), regardless of which of the two use cases is considered.
For input fields containers without a dimension index, this operation reduces to scalar multiplication.
- Parameters
-
outputData [out] - Output (dot product) data array. inputDataLeft [in] - Left input data array. inputDataRight [in] - Right input data array.
Definition at line 745 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::dotMultiplyDataData().
|
static |
Dot product of data and fields; please read the description below.
There are two use cases:
- dot product of a rank-3, 4 or 5 container inputFields with dimensions (C,F,P) (C,F,P,D1) or (C,F,P,D1,D2), representing the values of a set of scalar, vector or tensor fields, by the values in a rank-2, 3 or 4 container inputData indexed by (C,P), (C,P,D1), or (C,P,D1,D2) representing the values of scalar, vector or tensor data, OR
- dot product of a rank-2, 3 or 4 container inputFields with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or tensor field, by the values in a rank-2 container inputData indexed by (C,P), (C,P,D1) or (C,P,D1,D2), representing the values of scalar, vector or tensor data; the output value container outputFields is indexed by (C,F,P), regardless of which of the two use cases is considered.
For input fields containers without a dimension index, this operation reduces to scalar multiplication.
- Parameters
-
outputFields [out] - Output (dot product) fields array. inputData [in] - Data array. inputFields [in] - Input fields array.
Definition at line 729 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::dotMultiplyDataField().
|
static |
Computes point values outPointVals of a discrete function specified by the basis inFields and coefficients inCoeffs.
The array inFields with dimensions (C,F,P), (C,F,P,D1), or (C,F,P,D1,D2) represents the signed, transformed field (basis) values at points in REFERENCE frame; the outPointVals array with dimensions (C,P), (C,P,D1), or (C,P,D1,D2), respectively, represents values of a discrete function at points in PHYSICAL frame. The array inCoeffs dimensioned (C,F) supplies the coefficients for the field (basis) array.
Returns rank-2,3 or 4 array such that
![\[ outPointValues(c,p,*) = \sum_{f=0}^{F-1} \sigma_{c,f} u_{c,f}(x_p) \]](form_229.png)
where 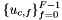 is scalar, vector or tensor valued finite element basis defined on physical cell
is scalar, vector or tensor valued finite element basis defined on physical cell 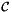 and
and 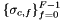 are the field signs of the basis functions; see Section Pullbacks. This method implements the last step in a four step process; please see Section Evaluation of finite element fields for details about the first three steps that prepare the necessary data for this method.
are the field signs of the basis functions; see Section Pullbacks. This method implements the last step in a four step process; please see Section Evaluation of finite element fields for details about the first three steps that prepare the necessary data for this method.
- Parameters
-
outputPointVals [out] - Output point values of a discrete function. inputCoeffs [in] - Coefficients associated with the fields (basis) array. inputFields [in] - Field (basis) values.
Definition at line 1166 of file Intrepid2_FunctionSpaceToolsDef.hpp.
|
inlinestatic |
Transformation of a 3D curl field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D).
Computes pullback of curls of HCURL functions 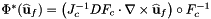 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 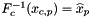 and the user-provided container should contain the curls of the vector function set
and the user-provided container should contain the curls of the vector function set 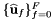 at the reference points:
at the reference points:
![\[ inputVals(f,p,*) = \nabla\times\widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_202.png)
The method returns
![\[ outputVals(c,f,p,*) = \left(J^{-1}_{c} DF_{c}\cdot\nabla\times\widehat{\bf u}_f\right)\circ F^{-1}_{c}(x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) DF_{c}(\widehat{x}_p)\cdot\nabla\times\widehat{\bf u}_f(\widehat{x}_p) \qquad 0\le c < C \,. \]](form_203.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
jacobianDividedByJacobianDet [in] - Input cell Jacobians, divided by their determinant. inputVals [in] - Input container of reference HDIV values.
- Returns
- lazily-evaluated transformed basis values.
Definition at line 238 of file Intrepid2_FunctionSpaceTools.hpp.
|
inlinestatic |
Transformation of a 2D curl field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P).
Computes pullback of curls of HCURL functions 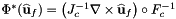 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 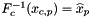 and the user-provided container should contain the 2d curls of the vector function set
and the user-provided container should contain the 2d curls of the vector function set 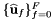 at the reference points:
at the reference points:
![\[ inputVals(f,p) = \nabla\times\widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_280.png)
The method returns
![\[ outputVals(c,f,p,*) = \left(J^{-1}_{c}\nabla\times\widehat{\bf u}_{f}\right) \circ F^{-1}_{c} (x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) \nabla\times\widehat{\bf u}_{f} (\widehat{x}_p) \qquad 0\le c < C \,. \]](form_281.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
outputVals [out] - Output array with transformed values jacobianDetInverse [in] - Reciprocals of input cell Jacobian determinants. inputVals [in] - Input array of reference HCURL curls.
Definition at line 288 of file Intrepid2_FunctionSpaceTools.hpp.
|
inlinestatic |
Transformation of a (vector) value field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D).
Computes pullback of HCURL functions 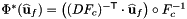 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 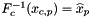 and the user-provided container should contain the values of the vector function set
and the user-provided container should contain the values of the vector function set 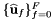 at the reference points:
at the reference points:
![\[ inputVals(f,p,*) = \widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_199.png)
The method returns
![\[ outputVals(c,f,p,*) = \left((DF_c)^{-{\sf T}}\cdot\widehat{\bf u}_f\right)\circ F^{-1}_{c}(x_{c,p}) = (DF_c)^{-{\sf T}}(\widehat{x}_p)\cdot\widehat{\bf u}_f(\widehat{x}_p) \qquad 0\le c < C \,. \]](form_200.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
jacobianInverse [in] - Input array containing cell Jacobian inverses. inputVals [in] - Input array of reference HCURL values.
- Returns
- lazily-evaluated transformed basis values.
Definition at line 189 of file Intrepid2_FunctionSpaceTools.hpp.
|
inlinestatic |
Transformation of a divergence field in the H-div space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P).
Computes pullback of the divergence of \e HDIV functions
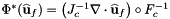 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 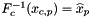 and the user-provided container should contain the divergencies of the vector function set
and the user-provided container should contain the divergencies of the vector function set 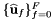 at the reference points:
at the reference points:
![\[ inputVals(f,p) = \nabla\cdot\widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_207.png)
The method returns
![\[ outputVals(c,f,p,*) = \left(J^{-1}_{c}\nabla\cdot\widehat{\bf u}_{f}\right) \circ F^{-1}_{c} (x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) \nabla\cdot\widehat{\bf u}_{f} (\widehat{x}_p) \qquad 0\le c < C \,. \]](form_208.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
jacobianDetInverse [in] - Reciprocals of input cell Jacobian determinants. refBasisDivValues [in] - Input container of reference HDIV divergences.
- Returns
- TransformedBasisValues object of logical shape (C,F,P).
Definition at line 386 of file Intrepid2_FunctionSpaceTools.hpp.
|
inlinestatic |
Transformation of a (vector) value field in the H-div space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D).
Computes pullback of HDIV functions 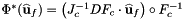 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 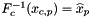 and the user-provided container should contain the values of the vector function set
and the user-provided container should contain the values of the vector function set 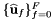 at the reference points:
at the reference points:
![\[ inputVals(f,p,*) = \widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_199.png)
The method returns
![\[ outputVals(c,f,p,*) = \left(J^{-1}_{c} DF_{c}\cdot \widehat{\bf u}_f\right)\circ F^{-1}_{c}(x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) DF_{c}(\widehat{x}_p)\cdot\widehat{\bf u}_f(\widehat{x}_p) \qquad 0\le c < C \,. \]](form_205.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
jacobianDividedByJacobianDet [in] - Input cell Jacobians, divided by their determinant. inputVals [in] - Input container of reference HDIV values.
- Returns
- TransformedBasisValues object of logical shape (C,F,P,D).
Definition at line 338 of file Intrepid2_FunctionSpaceTools.hpp.
|
inlinestatic |
Transformation of a gradient field in the H-grad space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D). The returned object contains the transformed gradient field, defined on cells in physical space and indexed by (C,F,P,D). The transformations are computed on entry access; algorithms such as sum factorization rely on having access to the reference-space basis values as well as the transformation operator; both are stored in the returned TransformedBasisValues object.
Computes pullback of gradients of \e HGRAD functions
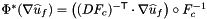 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 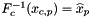 and the user-provided container should contain the gradients of the function set
and the user-provided container should contain the gradients of the function set 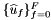 at the reference points:
at the reference points:
![\[ inputVals(f,p,*) = \nabla\widehat{u}_f(\widehat{x}_p) \,. \]](form_195.png)
The method returns
![\[ outputVals(c,f,p,*) = \left((DF_c)^{-{\sf T}}\cdot\nabla\widehat{u}_f\right)\circ F^{-1}_{c}(x_{c,p}) = (DF_c)^{-{\sf T}}(\widehat{x}_p)\cdot\nabla\widehat{u}_f(\widehat{x}_p) \qquad 0\le c < C \,. \]](form_196.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
jacobianInverse [in] - Input array containing cell Jacobian inverses. refBasisGradValues [in] - Input array of reference HGRAD gradients.
- Returns
- TransformedBasisValues object defined on (C,F,P,D) indices; transformation is computed on access.
Definition at line 97 of file Intrepid2_FunctionSpaceTools.hpp.
|
inlinestatic |
Transformation of a (scalar) value field in the H-grad space, defined at points on a reference cell, stored in the user-provided container input and indexed by (F,P), into the output container output, defined on cells in physical space and indexed by (C,F,P). This transformation is trivial, and the returned container is logically indexed by (C,F,P), but only contains (F,P) distinct data entries.
Computes pullback of HGRAD functions 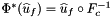 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 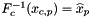 and the user-provided container should contain the values of the function set
and the user-provided container should contain the values of the function set 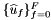 at the reference points:
at the reference points:
![\[ input(f,p) = \widehat{u}_f(\widehat{x}_p) \,. \]](form_192.png)
The method returns
![\[ output(c,f,p) = \widehat{u}_f\circ F^{-1}_{c}(x_{c,p}) = \widehat{u}_f(\widehat{x}_p) = input(f,p) \qquad 0\le c < C \,, \]](form_193.png)
i.e., it simply replicates the values in the user-provided container to every cell. See Section Pullbacks for more details about pullbacks.
- Parameters
-
input [in] - Input container of reference HGRAD values.
- Returns
- TransformedBasisValues object of logical shape (C,F,P).
Definition at line 143 of file Intrepid2_FunctionSpaceTools.hpp.
|
inlinestatic |
Transformation of a (scalar) value field in the H-vol space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P).
Computes pullback of HVOL functions 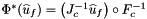 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 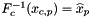 and the user-provided container should contain the values of the functions in the set
and the user-provided container should contain the values of the functions in the set 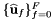 at the reference points:
at the reference points:
![\[ inputVals(f,p) = \widehat{u}_f(\widehat{x}_p) \,. \]](form_210.png)
The method returns
![\[ outputVals(c,f,p,*) = \left(J^{-1}_{c}\widehat{u}_{f}\right) \circ F^{-1}_{c} (x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) \widehat{u}_{f} (\widehat{x}_p) \qquad 0\le c < C \,. \]](form_211.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
jacobianDetInverse [in] - Reciprocals of input cell Jacobian determinants. refBasisValues [in] - Input container of reference HVOL values.
- Returns
- TransformedBasisValues object of logical shape (C,F,P).
Definition at line 434 of file Intrepid2_FunctionSpaceTools.hpp.
|
static |
Transformation of a 3D curl field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D).
Computes pullback of curls of HCURL functions 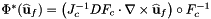 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 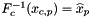 and the user-provided container should contain the curls of the vector function set
and the user-provided container should contain the curls of the vector function set 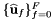 at the reference points:
at the reference points:
![\[ inputVals(f,p,*) = \nabla\times\widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_202.png)
The method returns
![\[ outputVals(c,f,p,*) = \left(J^{-1}_{c} DF_{c}\cdot\nabla\times\widehat{\bf u}_f\right)\circ F^{-1}_{c}(x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) DF_{c}(\widehat{x}_p)\cdot\nabla\times\widehat{\bf u}_f(\widehat{x}_p) \qquad 0\le c < C \,. \]](form_203.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
outputVals [out] - Output array with transformed values jacobian [in] - Input array containing cell Jacobians. jacobianDet [in] - Input array containing cell Jacobian determinants. inputVals [in] - Input array of reference HCURL curls.
Definition at line 242 of file Intrepid2_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a 2D curl field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P).
Computes pullback of curls of HCURL functions 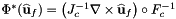 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 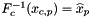 and the user-provided container should contain the 2d curls of the vector function set
and the user-provided container should contain the 2d curls of the vector function set 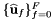 at the reference points:
at the reference points:
![\[ inputVals(f,p) = \nabla\times\widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_280.png)
The method returns
![\[ outputVals(c,f,p,*) = \left(J^{-1}_{c}\nabla\times\widehat{\bf u}_{f}\right) \circ F^{-1}_{c} (x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) \nabla\times\widehat{\bf u}_{f} (\widehat{x}_p) \qquad 0\le c < C \,. \]](form_281.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
outputVals [out] - Output array with transformed values jacobianDet [in] - Input array containing cell Jacobian determinants. inputVals [in] - Input array of reference HCURL curls.
Definition at line 260 of file Intrepid2_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a (vector) value field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D).
Computes pullback of HCURL functions 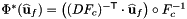 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 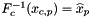 and the user-provided container should contain the values of the vector function set
and the user-provided container should contain the values of the vector function set 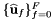 at the reference points:
at the reference points:
![\[ inputVals(f,p,*) = \widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_199.png)
The method returns
![\[ outputVals(c,f,p,*) = \left((DF_c)^{-{\sf T}}\cdot\widehat{\bf u}_f\right)\circ F^{-1}_{c}(x_{c,p}) = (DF_c)^{-{\sf T}}(\widehat{x}_p)\cdot\widehat{\bf u}_f(\widehat{x}_p) \qquad 0\le c < C \,. \]](form_200.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
outputVals [out] - Output array with transformed values jacobianInverse [in] - Input array containing cell Jacobian inverses. inputVals [in] - Input array of reference HCURL values.
Definition at line 120 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::matvecProductDataField().
|
static |
Transformation of a divergence field in the H-div space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P).
Computes pullback of the divergence of HDIV functions 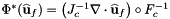 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 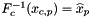 and the user-provided container should contain the divergencies of the vector function set
and the user-provided container should contain the divergencies of the vector function set 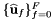 at the reference points:
at the reference points:
![\[ inputVals(f,p) = \nabla\cdot\widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_207.png)
The method returns
![\[ outputVals(c,f,p,*) = \left(J^{-1}_{c}\nabla\cdot\widehat{\bf u}_{f}\right) \circ F^{-1}_{c} (x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) \nabla\cdot\widehat{\bf u}_{f} (\widehat{x}_p) \qquad 0\le c < C \,. \]](form_208.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
outputVals [out] - Output array with transformed values jacobianDet [in] - Input array containing cell Jacobian determinants. inputVals [in] - Input array of reference HDIV divergences.
Definition at line 351 of file Intrepid2_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a (vector) value field in the H-div space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D).
Computes pullback of HDIV functions 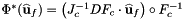 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 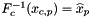 and the user-provided container should contain the values of the vector function set
and the user-provided container should contain the values of the vector function set 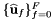 at the reference points:
at the reference points:
![\[ inputVals(f,p,*) = \widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_199.png)
The method returns
![\[ outputVals(c,f,p,*) = \left(J^{-1}_{c} DF_{c}\cdot \widehat{\bf u}_f\right)\circ F^{-1}_{c}(x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) DF_{c}(\widehat{x}_p)\cdot\widehat{\bf u}_f(\widehat{x}_p) \qquad 0\le c < C \,. \]](form_205.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
outputVals [out] - Output array with transformed values jacobian [in] - Input array containing cell Jacobians. jacobianDet [in] - Input array containing cell Jacobian determinants. inputVals [in] - Input array of reference HDIV values.
Definition at line 303 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::matvecProductDataField(), and Intrepid2::ArrayTools< DeviceType >::scalarMultiplyDataField().
|
static |
Transformation of a 2D curl field in the H-grad space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D).
Computes pullback of curls of 2D HGRAD functions 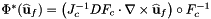 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 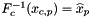 and the user-provided container should contain the curls of the vector function set
and the user-provided container should contain the curls of the vector function set 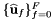 at the reference points:
at the reference points:
![\[ inputVals(f,p,*) = \nabla\times\widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_202.png)
The method returns
![\[ outputVals(c,f,p,*) = \left(J^{-1}_{c} DF_{c}\cdot\nabla\times\widehat{\bf u}_f\right)\circ F^{-1}_{c}(x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) DF_{c}(\widehat{x}_p)\cdot\nabla\times\widehat{\bf u}_f(\widehat{x}_p) \qquad 0\le c < C \,. \]](form_203.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
outputVals [out] - Output array with transformed values jacobian [in] - Input array containing cell Jacobians. jacobianDet [in] - Input array containing cell Jacobian determinants. inputVals [in] - Input array of reference HDIV values.
Definition at line 281 of file Intrepid2_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a gradient field in the H-grad space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P,D), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P,D).
Computes pullback of gradients of HGRAD functions 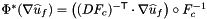 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 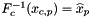 and the user-provided container should contain the gradients of the function set
and the user-provided container should contain the gradients of the function set 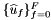 at the reference points:
at the reference points:
![\[ inputVals(f,p,*) = \nabla\widehat{u}_f(\widehat{x}_p) \,. \]](form_195.png)
The method returns
![\[ outputVals(c,f,p,*) = \left((DF_c)^{-{\sf T}}\cdot\nabla\widehat{u}_f\right)\circ F^{-1}_{c}(x_{c,p}) = (DF_c)^{-{\sf T}}(\widehat{x}_p)\cdot\nabla\widehat{u}_f(\widehat{x}_p) \qquad 0\le c < C \,. \]](form_196.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
outputVals [out] - Output array with transformed values jacobianInverse [in] - Input array containing cell Jacobian inverses. inputVals [in] - Input array of reference HGRAD gradients.
Definition at line 106 of file Intrepid2_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a (scalar) value field in the H-grad space, defined at points on a reference cell, stored in the user-provided container input and indexed by (F,P), into the output container output, defined on cells in physical space and indexed by (C,F,P).
Computes pullback of HGRAD functions 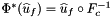 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 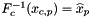 and the user-provided container should contain the values of the function set
and the user-provided container should contain the values of the function set 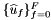 at the reference points:
at the reference points:
![\[ input(f,p) = \widehat{u}_f(\widehat{x}_p) \,. \]](form_192.png)
The method returns
![\[ output(c,f,p) = \widehat{u}_f\circ F^{-1}_{c}(x_{c,p}) = \widehat{u}_f(\widehat{x}_p) = input(f,p) \qquad 0\le c < C \,, \]](form_193.png)
i.e., it simply replicates the values in the user-provided container to every cell. See Section Pullbacks for more details about pullbacks.
- Parameters
-
output [out] - Output array with transformed values input [in] - Input array of reference HGRAD values.
Definition at line 31 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::RealSpaceTools< DeviceType >::clone(), and Intrepid2::ArrayTools< DeviceType >::cloneFields().
|
static |
Transformation of a (scalar) value field in the H-vol space, defined at points on a reference cell, stored in the user-provided container inputVals and indexed by (F,P), into the output container outputVals, defined on cells in physical space and indexed by (C,F,P).
Computes pullback of HVOL functions 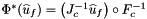 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_189.png)
In this case 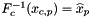 and the user-provided container should contain the values of the functions in the set
and the user-provided container should contain the values of the functions in the set 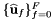 at the reference points:
at the reference points:
![\[ inputVals(f,p) = \widehat{u}_f(\widehat{x}_p) \,. \]](form_210.png)
The method returns
![\[ outputVals(c,f,p,*) = \left(J^{-1}_{c}\widehat{u}_{f}\right) \circ F^{-1}_{c} (x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) \widehat{u}_{f} (\widehat{x}_p) \qquad 0\le c < C \,. \]](form_211.png)
See Section Pullbacks for more details about pullbacks.
- Parameters
-
outputVals [out] - Output array with transformed values jacobianDet [in] - Input array containing cell Jacobian determinants. inputVals [in] - Input array of reference HVOL values.
Definition at line 365 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::scalarMultiplyDataField().
|
static |
Contracts leftValues and rightValues arrays on the point and possibly space dimensions and stores the result in outputValues; this is a generic, high-level integration routine that calls either FunctionSpaceTools::operatorIntegral, or FunctionSpaceTools::functionalIntegral, or FunctionSpaceTools::dataIntegral methods, depending on the rank of the outputValues array.
- Parameters
-
outputValues [out] - Output array. leftValues [in] - Left input array. rightValues [in] - Right input array. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE.
Definition at line 393 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::contractDataDataScalar(), Intrepid2::ArrayTools< DeviceType >::contractDataDataTensor(), Intrepid2::ArrayTools< DeviceType >::contractDataDataVector(), Intrepid2::ArrayTools< DeviceType >::contractDataFieldScalar(), Intrepid2::ArrayTools< DeviceType >::contractDataFieldTensor(), Intrepid2::ArrayTools< DeviceType >::contractDataFieldVector(), Intrepid2::ArrayTools< DeviceType >::contractFieldFieldScalar(), Intrepid2::ArrayTools< DeviceType >::contractFieldFieldTensor(), and Intrepid2::ArrayTools< DeviceType >::contractFieldFieldVector().
Referenced by Intrepid2::ProjectionTools< DeviceType >::getHCurlBasisCoeffs(), Intrepid2::ProjectionTools< DeviceType >::getHDivBasisCoeffs(), Intrepid2::ProjectionTools< DeviceType >::getHGradBasisCoeffs(), Intrepid2::ProjectionTools< DeviceType >::getL2BasisCoeffs(), and Intrepid2::ProjectionTools< DeviceType >::getL2DGBasisCoeffs().
|
static |
Transformation of 3D HCURL data from physical side to reference side. It takes the input vector 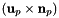 defined on physical sides and maps it into
defined on physical sides and maps it into 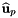 on the reference side.
on the reference side. 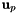 is a 3D HCURL function evaluated at points
is a 3D HCURL function evaluated at points 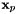 ,
, 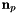 the outer unit normal to the sides at point
the outer unit normal to the sides at point 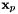 and
and 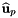 is a 2D HCURL function evaluated at reference points
is a 2D HCURL function evaluated at reference points 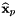 .
.
![\[ \widehat{\bf u}_p = \left[ \begin{array}{cc} 0 & -1\\ 1 & 0 \end{array} \right] \sqrt{\text{det}(T^T T)}\; (T^T T)^{-1}\; T^T\; ({\bf u}_p \times {\bf n}_p ) \]](form_320.png)
here 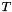 is a 3x2 matrix, whose columns are the two physical side tangents, computed differentiating the parameterization of the physical side (see CellTools::getPhysicalFaceTangents).
is a 3x2 matrix, whose columns are the two physical side tangents, computed differentiating the parameterization of the physical side (see CellTools::getPhysicalFaceTangents).
- Parameters
-
outputVals [out] - 2D HCURL function in reference space, indexed by (C,P,2). tangents [in] - physical tangents (T) computed differentiating the parameterization of the physical sides, indexed by (C,P,3,2) metricTensorInv [in] - Inverse of the metric tensor 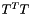 , indexed by (C,P,2,2).
, indexed by (C,P,2,2). metricTensorDet [in] - determinant of the metric tensor 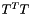 , indexed by (C,P).
, indexed by (C,P). inputVals [in] - cross product of a HCURL function with the unit outer normals to the sides, indexed by (C,P,3)
Definition at line 175 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::matvecProductDataData().
|
static |
Transformation of 2D HCURL data from physical side to reference side. It takes the input scalar 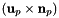 defined on physical sides and maps it into
defined on physical sides and maps it into 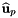 on the reference side.
on the reference side. 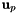 is a 2D HCURL function evaluated at points
is a 2D HCURL function evaluated at points 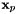 ,
, 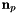 the unit outer normal to the sides at point
the unit outer normal to the sides at point 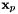 and
and 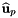 is a 2D HVOL function evaluated at reference points
is a 2D HVOL function evaluated at reference points 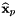 . Note,
. Note, 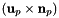 is computed by extending the 2D vectors (in xy plane) to the 3D space, and taking only the component of the cross product in the z-axis direction.
is computed by extending the 2D vectors (in xy plane) to the 3D space, and taking only the component of the cross product in the z-axis direction.
![\[ \widehat{\bf u}_p = - \sqrt{\text{det}(T^T T)} \; ({\bf u}_p \times {\bf n}_p ) \]](form_323.png)
here 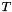 is the side physical tangent, computed differentiating the parameterization of the physical side (see CellTools::getPhysicalEdgeTangents).
is the side physical tangent, computed differentiating the parameterization of the physical side (see CellTools::getPhysicalEdgeTangents).
- Parameters
-
outputVals [out] - HVOL function in reference space, indexed by (C,P). metricTensorDet [in] - determinant of the metric tensor 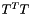 , indexed by (C,P). Note, this is also the norm squared of the edge tangents
, indexed by (C,P). Note, this is also the norm squared of the edge tangents inputVals [in] - scalar cross product of a (2D) HCURL function with the unit outer normals to the edges, indexed by (C,P)
Definition at line 225 of file Intrepid2_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a (vector) data in the H-curl space, defined in the physical space, stored in the user-provided container inputVals and indexed by (C,P,D), into the output container outputVals, defined on the reference cell and indexed by (C,P,D).
Computes the map 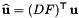
where 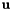 is the input HCURL data in the physical space, evaluated at points
is the input HCURL data in the physical space, evaluated at points 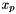 ,
, 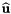 is the output HCURL data on the reference cell evaluated at the reference points
is the output HCURL data on the reference cell evaluated at the reference points 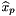 and
and 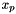 is the point on physical side corresponding to the the point
is the point on physical side corresponding to the the point 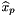 on the reference cell, through the map
on the reference cell, through the map 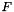 .
. 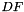 is the Jacobian of the map
is the Jacobian of the map 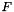 .
.
- Parameters
-
outputVals [out] - Output array with reference HCURL data, indexed by (C,P,D) jacobian [in] - Input array containing the Jacobian, indexed by (C,P,D,D) inputVals [in] - Input array of HCURL data in physical space, indexed by (C,P,D).
Definition at line 132 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::matvecProductDataData().
|
static |
Transformation of HDIV data from physical side to reference side. It takes the input 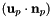 defined on physical sides and maps it into
defined on physical sides and maps it into 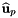 on the reference side.
on the reference side. 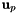 is a HDIV function evaluated at points
is a HDIV function evaluated at points 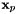 ,
, 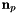 the outer unit normal to the sides at point
the outer unit normal to the sides at point 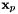 and
and 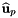 is a HVOL data evaluated at reference points
is a HVOL data evaluated at reference points 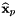 .
.
It computes
![\[ \widehat{\bf u}_p = \sqrt{\text{det}(T^T T)}\; ({\bf u}_p \cdot {\bf n}_p ) \]](form_327.png)
here 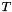 is a 3x2 matrix, whose columns are the two physical side tangents, computed differentiating the parameterization of the physical side (see CellTools::getPhysicalFaceTangents and var>CellTools::getPhysicalEdgeTangents). Note {det}(T^T T)} is equivalent to the square of the norm of the physical normal computed with CellTools::getPhysicalSideNormal.
is a 3x2 matrix, whose columns are the two physical side tangents, computed differentiating the parameterization of the physical side (see CellTools::getPhysicalFaceTangents and var>CellTools::getPhysicalEdgeTangents). Note {det}(T^T T)} is equivalent to the square of the norm of the physical normal computed with CellTools::getPhysicalSideNormal.
- Parameters
-
outputVals [out] - HVOL data in reference space, indexed by (C,P). metricTensorDet [in] - determinant of the metric tensor 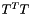 , indexed by (C,P).
, indexed by (C,P). inputVals [in] - HDIV function dotted with the unit outer normals to the sides, indexed by (C,P)
Definition at line 335 of file Intrepid2_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a (vector) data in the H-div space, defined in the physical space, stored in the user-provided container inputVals and indexed by (C,P,D), into the output container outputVals, defined on the reference cell and indexed by (C,P,D).
Computes the map 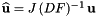
where 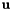 is the input HDIV data in the physical space, evaluated at points
is the input HDIV data in the physical space, evaluated at points 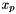 ,
, 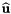 is the output HDIV data on the reference cell evaluated at the reference points
is the output HDIV data on the reference cell evaluated at the reference points 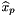 and
and 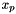 is the point on physical side corresponding to the the point
is the point on physical side corresponding to the the point 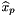 on the reference cell, through the map
on the reference cell, through the map 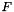 .
. 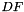 is the Jacobian of the map
is the Jacobian of the map 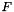 , and
, and 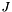 its determinant
its determinant
- Parameters
-
outputVals [out] - Output array with reference HDIV data, indexed by (C,P,D) jacobianInverse [in] - Input array containing the Jacobian inverse, indexed by (C,P,D,D) jacobianDet [in] - Input array containing the Jacobian determinant, indexed by (C,P) inputVals [in] - Input array of HDIV data in physical space, indexed by (C,P,D).
Definition at line 318 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::matvecProductDataData(), and Intrepid2::ArrayTools< DeviceType >::scalarMultiplyDataData().
|
static |
Transformation of a (scalar) data in the H-grad space, defined in physical space, stored in the user-provided container input and indexed by (C,P), into the output container output, defined on reference sides and indexed by (C,P). It computes 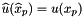 where
where 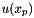 is the input H-grad data on physical sides,
is the input H-grad data on physical sides, 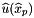 is the output H-grad data on the reference side, and
is the output H-grad data on the reference side, and 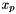 is the point on physical side corresponding to the the point
is the point on physical side corresponding to the the point 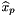 on the reference side. Essentially this function copies the input into the output.
on the reference side. Essentially this function copies the input into the output.
- Parameters
-
output [out] - Output array of HGRAD data on reference side, indexed by (C,P) input [in] - Input array of HGRAD data on physical side (C,P)
Definition at line 75 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::RealSpaceTools< DeviceType >::clone(), and Intrepid2::ArrayTools< DeviceType >::cloneFields().
|
static |
Transformation of a (scalar) data in the H-grad space, defined in physical space, stored in the user-provided container input and indexed by (C,P), into the output container output, defined on reference cells and indexed by (C,P). It computes 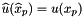 where
where 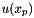 is the input H-grad data,
is the input H-grad data, 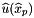 is the output H-grad data in the reference frame, and
is the output H-grad data in the reference frame, and 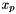 is the point in physical space corresponding to the the point
is the point in physical space corresponding to the the point 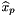 in the reference frame. Essentially this function copies the input into the output.
in the reference frame. Essentially this function copies the input into the output.
- Parameters
-
output [out] - Output array of HGRAD data in the reference cell, indexed by (C,P) input [in] - Input array of HGRAD data in physical space (C,P)
Definition at line 53 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::RealSpaceTools< DeviceType >::clone(), and Intrepid2::ArrayTools< DeviceType >::cloneFields().
|
static |
Transformation of a (scalar) data in the H-vol space, defined in the physical space, stored in the user-provided container inputVals and indexed by (C,P), into the output container outputVals, defined on the reference cell and indexed by (C,P).
Computes the map 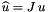
where 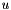 is the input HVOL data in the physical space, evaluated at points
is the input HVOL data in the physical space, evaluated at points 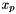 ,
, 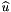 is the output HVOL data on the reference cell evaluated at the reference points
is the output HVOL data on the reference cell evaluated at the reference points 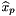 and
and 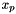 is the point on physical side corresponding to the the point
is the point on physical side corresponding to the the point 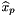 on the reference cell, through the map
on the reference cell, through the map 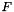 .
. 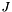 is the determinant of the Jacobian of the map
is the determinant of the Jacobian of the map 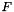 .
.
- Parameters
-
outputVals [out] - Output array with reference HVOL data, indexed by (C,P) jacobianDet [in] - Input array containing the Jacobian determinant, indexed by (C,P) inputVals [in] - Input array of HVOL data in physical space, indexed by (C,P).
Definition at line 377 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::scalarMultiplyDataData().
|
static |
Multiplies fields inputVals by weighted measures inputMeasure and returns the field array outputVals; this is a simple redirection to the call FunctionSpaceTools::scalarMultiplyDataField.
- Parameters
-
outputVals [out] - Output array with scaled field values. inputMeasure [in] - Input array containing weighted measures. inputVals [in] - Input fields.
Definition at line 676 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::scalarMultiplyDataField().
|
static |
Scalar multiplication of data and data; please read the description below.
There are two use cases:
- multiplies a rank-2, 3, or 4 container inputDataRight with dimensions (C,P), (C,P,D1) or (C,P,D1,D2), representing the values of a set of scalar, vector or tensor data, by the values in a rank-2 container inputDataLeft indexed by (C,P), representing the values of scalar data, OR
- multiplies a rank-1, 2, or 3 container inputDataRight with dimensions (P), (P,D1) or (P,D1,D2), representing the values of scalar, vector or tensor data, by the values in a rank-2 container inputDataLeft indexed by (C,P), representing the values of scalar data; the output value container outputData is indexed by (C,P), (C,P,D1) or (C,P,D1,D2), regardless of which of the two use cases is considered.
- Note
- The arguments inputDataLeft, inputDataRight can be changed! This enables in-place multiplication.
- Parameters
-
outputData [out] - Output data array. inputDataLeft [in] - Left (multiplying) data array. inputDataRight [in] - Right (being multiplied) data array. reciprocal [in] - If TRUE, divides input fields by the data (instead of multiplying). Default: FALSE.
Definition at line 711 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::scalarMultiplyDataData().
|
static |
Scalar multiplication of data and fields; please read the description below.
There are two use cases:
- multiplies a rank-3, 4, or 5 container inputFields with dimensions (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2), representing the values of a set of scalar, vector or tensor fields, by the values in a rank-2 container inputData indexed by (C,P), representing the values of scalar data, OR
- multiplies a rank-2, 3, or 4 container inputFields with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or a tensor field, by the values in a rank-2 container inputData indexed by (C,P), representing the values of scalar data; the output value container outputFields is indexed by (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2), regardless of which of the two use cases is considered.
- Note
- The argument inputFields can be changed! This enables in-place multiplication.
- Parameters
-
outputFields [out] - Output (product) fields array. inputData [in] - Data (multiplying) array. inputFields [in] - Input (being multiplied) fields array. reciprocal [in] - If TRUE, divides input fields by the data (instead of multiplying). Default: FALSE.
Definition at line 693 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::scalarMultiplyDataField().
|
static |
Matrix-vector or matrix-matrix product of data and data; please read the description below.
There are four use cases:
- matrix-vector product of a rank-3 container inputDataRight with dimensions (C,P,D), representing the values of a set of vector data, on the left by the values in a rank-2, 3, or 4 container inputDataLeft indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data, OR
- matrix-vector product of a rank-2 container inputDataRight with dimensions (P,D), representing the values of vector data, on the left by the values in a rank-2, 3, or 4 container inputDataLeft indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data, OR
- matrix-matrix product of a rank-4 container inputDataRight with dimensions (C,P,D,D), representing the values of a set of tensor data, on the left by the values in a rank-2, 3, or 4 container inputDataLeft indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data, OR
- matrix-matrix product of a rank-3 container inputDataRight with dimensions (P,D,D), representing the values of tensor data, on the left by the values in a rank-2, 3, or 4 container inputDataLeft indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data; for matrix-vector products, the output value container outputData is indexed by (C,P,D); for matrix-matrix products, the output value container outputData is indexed by (C,P,D1,D2).
- Remarks
- The rank of inputDataLeft implicitly defines the type of tensor data:
- rank = 2 corresponds to a constant diagonal tensor
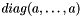
- rank = 3 corresponds to a nonconstant diagonal tensor
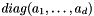
- rank = 4 corresponds to a full tensor
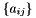
- rank = 2 corresponds to a constant diagonal tensor
- Note
- It is assumed that all tensors are square!
- The method is defined for spatial dimensions D = 1, 2, 3
- Parameters
-
outputData [out] - Output (matrix-vector product) data array. inputDataLeft [in] - Left input data array. inputDataRight [in] - Right input data array. transpose [in] - If 'T', use transposed tensor; if 'N', no transpose. Default: 'N'.
Definition at line 857 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::matmatProductDataData(), and Intrepid2::ArrayTools< DeviceType >::matvecProductDataData().
|
static |
Matrix-vector or matrix-matrix product of data and fields; please read the description below.
There are four use cases:
- matrix-vector product of a rank-4 container inputFields with dimensions (C,F,P,D), representing the values of a set of vector fields, on the left by the values in a rank-2, 3, or 4 container inputData indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data, OR
- matrix-vector product of a rank-3 container inputFields with dimensions (F,P,D), representing the values of a vector field, on the left by the values in a rank-2, 3, or 4 container inputData indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data, OR
- matrix-matrix product of a rank-5 container inputFields with dimensions (C,F,P,D,D), representing the values of a set of tensor fields, on the left by the values in a rank-2, 3, or 4 container inputData indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data, OR
- matrix-matrix product of a rank-4 container inputFields with dimensions (F,P,D,D), representing the values of a tensor field, on the left by the values in a rank-2, 3, or 4 container inputData indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data; for matrix-vector products, the output value container outputFields is indexed by (C,F,P,D); for matrix-matrix products the output value container outputFields is indexed by (C,F,P,D,D).
- Remarks
- The rank of inputData implicitly defines the type of tensor data:
- rank = 2 corresponds to a constant diagonal tensor
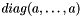
- rank = 3 corresponds to a nonconstant diagonal tensor
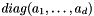
- rank = 4 corresponds to a full tensor
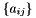
- rank = 2 corresponds to a constant diagonal tensor
- Note
- It is assumed that all tensors are square!
- The method is defined for spatial dimensions D = 1, 2, 3
- Parameters
-
outputFields [out] - Output (matrix-vector or matrix-matrix product) fields array. inputData [in] - Data array. inputFields [in] - Input fields array. transpose [in] - If 'T', use transposed left data tensor; if 'N', no transpose. Default: 'N'.
Definition at line 823 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::matmatProductDataField(), and Intrepid2::ArrayTools< DeviceType >::matvecProductDataField().
|
static |
Cross or outer product of data and data; please read the description below.
There are four use cases:
- cross product of a rank-3 container inputDataRight with dimensions (C,P,D), representing the values of a set of vector data, on the left by the values in a rank-3 container inputDataLeft indexed by (C,P,D) representing the values of vector data, OR
- cross product of a rank-2 container inputDataRight with dimensions (P,D), representing the values of vector data, on the left by the values in a rank-3 container inputDataLeft indexed by (C,P,D), representing the values of vector data, OR
- outer product of a rank-3 container inputDataRight with dimensions (C,P,D), representing the values of a set of vector data, on the left by the values in a rank-3 container inputDataLeft indexed by (C,P,D) representing the values of vector data, OR
- outer product of a rank-2 container inputDataRight with dimensions (P,D), representing the values of vector data, on the left by the values in a rank-3 container inputDataLeft indexed by (C,P,D), representing the values of vector data; for cross products, the output value container outputData is indexed by (C,P,D) in 3D (vector output) and by (C,P) in 2D (scalar output); for outer products, the output value container outputData is indexed by (C,P,D,D).
- Parameters
-
outputData [out] - Output (cross or outer product) data array. inputDataLeft [in] - Left input data array. inputDataRight [in] - Right input data array.
Definition at line 792 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::crossProductDataData(), and Intrepid2::ArrayTools< DeviceType >::outerProductDataData().
|
static |
Cross or outer product of data and fields; please read the description below.
There are four use cases:
- cross product of a rank-4 container inputFields with dimensions (C,F,P,D), representing the values of a set of vector fields, on the left by the values in a rank-3 container inputData indexed by (C,P,D), representing the values of vector data, OR
- cross product of a rank-3 container inputFields with dimensions (F,P,D), representing the values of a vector field, on the left by the values in a rank-3 container inputData indexed by (C,P,D), representing the values of vector data, OR
- outer product of a rank-4 container inputFields with dimensions (C,F,P,D), representing the values of a set of vector fields, on the left by the values in a rank-3 container inputData indexed by (C,P,D), representing the values of vector data, OR
- outer product of a rank-3 container inputFields with dimensions (F,P,D), representing the values of a vector field, on the left by the values in a rank-3 container inputData indexed by (C,P,D), representing the values of vector data; for cross products, the output value container outputFields is indexed by (C,F,P,D) in 3D (vector output) and by (C,F,P) in 2D (scalar output); for outer products, the output value container outputFields is indexed by (C,F,P,D,D).
- Parameters
-
outputFields [out] - Output (cross or outer product) fields array. inputData [in] - Data array. inputFields [in] - Input fields array.
Definition at line 761 of file Intrepid2_FunctionSpaceToolsDef.hpp.
References Intrepid2::ArrayTools< DeviceType >::crossProductDataField(), and Intrepid2::ArrayTools< DeviceType >::outerProductDataField().
The documentation for this class was generated from the following files:
- http://docs.trilinos.org/dev/packages/intrepid2/src/Discretization/FunctionSpaceTools/Intrepid2_FunctionSpaceTools.hpp
- http://docs.trilinos.org/dev/packages/intrepid2/src/Discretization/FunctionSpaceTools/Intrepid2_FunctionSpaceToolsDef.hpp
 1.8.5
1.8.5