Defines expert-level interfaces for the evaluation of functions and operators in physical space (supported for FE, FV, and FD methods) and FE reference space; in addition, provides several function transformation utilities. More...
#include <Intrepid_FunctionSpaceTools.hpp>
Static Public Member Functions | |
| template<class Scalar , class ArrayTypeOut , class ArrayTypeIn > | |
| static void | HGRADtransformVALUE (ArrayTypeOut &outVals, const ArrayTypeIn &inVals) |
| Transformation of a (scalar) value field in the H-grad space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P), into the output container outVals, defined on cells in physical space and indexed by (C,F,P). More... | |
| template<class Scalar , class ArrayTypeOut , class ArrayTypeJac , class ArrayTypeIn > | |
| static void | HGRADtransformGRAD (ArrayTypeOut &outVals, const ArrayTypeJac &jacobianInverse, const ArrayTypeIn &inVals, const char transpose= 'T') |
| Transformation of a gradient field in the H-grad space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P,D), into the output container outVals, defined on cells in physical space and indexed by (C,F,P,D). More... | |
| template<class Scalar , class ArrayTypeOut , class ArrayTypeJac , class ArrayTypeIn > | |
| static void | HCURLtransformVALUE (ArrayTypeOut &outVals, const ArrayTypeJac &jacobianInverse, const ArrayTypeIn &inVals, const char transpose= 'T') |
| Transformation of a (vector) value field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P,D), into the output container outVals, defined on cells in physical space and indexed by (C,F,P,D). More... | |
| template<class Scalar , class ArrayTypeOut , class ArrayTypeJac , class ArrayTypeDet , class ArrayTypeIn > | |
| static void | HCURLtransformCURL (ArrayTypeOut &outVals, const ArrayTypeJac &jacobian, const ArrayTypeDet &jacobianDet, const ArrayTypeIn &inVals, const char transpose= 'N') |
| Transformation of a curl field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P,D), into the output container outVals, defined on cells in physical space and indexed by (C,F,P,D). More... | |
| template<class Scalar , class ArrayTypeOut , class ArrayTypeJac , class ArrayTypeDet , class ArrayTypeIn > | |
| static void | HDIVtransformVALUE (ArrayTypeOut &outVals, const ArrayTypeJac &jacobian, const ArrayTypeDet &jacobianDet, const ArrayTypeIn &inVals, const char transpose= 'N') |
| Transformation of a (vector) value field in the H-div space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P,D), into the output container outVals, defined on cells in physical space and indexed by (C,F,P,D). More... | |
| template<class Scalar , class ArrayTypeOut , class ArrayTypeDet , class ArrayTypeIn > | |
| static void | HDIVtransformDIV (ArrayTypeOut &outVals, const ArrayTypeDet &jacobianDet, const ArrayTypeIn &inVals) |
| Transformation of a divergence field in the H-div space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P), into the output container outVals, defined on cells in physical space and indexed by (C,F,P). More... | |
| template<class Scalar , class ArrayTypeOut , class ArrayTypeDet , class ArrayTypeIn > | |
| static void | HVOLtransformVALUE (ArrayTypeOut &outVals, const ArrayTypeDet &jacobianDet, const ArrayTypeIn &inVals) |
| Transformation of a (scalar) value field in the H-vol space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P), into the output container outVals, defined on cells in physical space and indexed by (C,F,P). More... | |
| template<class Scalar > | |
| static void | integrate (Intrepid::FieldContainer< Scalar > &outputValues, const Intrepid::FieldContainer< Scalar > &leftValues, const Intrepid::FieldContainer< Scalar > &rightValues, const ECompEngine compEngine, const bool sumInto=false) |
| Contracts leftValues and rightValues arrays on the point and possibly space dimensions and stores the result in outputValues; this is a generic, high-level integration routine that calls either FunctionSpaceTools::operatorIntegral, or FunctionSpaceTools::functionalIntegral, or FunctionSpaceTools::dataIntegral methods, depending on the rank of the outputValues array. More... | |
| template<class Scalar , class ArrayOut , class ArrayInLeft , class ArrayInRight > | |
| static void | integrate (ArrayOut &outputValues, const ArrayInLeft &leftValues, const ArrayInRight &rightValues, const ECompEngine compEngine, const bool sumInto=false) |
| template<class Scalar , class ArrayOutFields , class ArrayInFieldsLeft , class ArrayInFieldsRight > | |
| static void | operatorIntegral (ArrayOutFields &outputFields, const ArrayInFieldsLeft &leftFields, const ArrayInFieldsRight &rightFields, const ECompEngine compEngine, const bool sumInto=false) |
| Contracts the point (and space) dimensions P (and D1 and D2) of two rank-3, 4, or 5 containers with dimensions (C,L,P) and (C,R,P), or (C,L,P,D1) and (C,R,P,D1), or (C,L,P,D1,D2) and (C,R,P,D1,D2), and returns the result in a rank-3 container with dimensions (C,L,R). More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | functionalIntegral (ArrayOutFields &outputFields, const ArrayInData &inputData, const ArrayInFields &inputFields, const ECompEngine compEngine, const bool sumInto=false) |
| Contracts the point (and space) dimensions P (and D1 and D2) of a rank-3, 4, or 5 container and a rank-2, 3, or 4 container, respectively, with dimensions (C,F,P) and (C,P), or (C,F,P,D1) and (C,P,D1), or (C,F,P,D1,D2) and (C,P,D1,D2), respectively, and returns the result in a rank-2 container with dimensions (C,F). More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | dataIntegral (ArrayOutData &outputData, const ArrayInDataLeft &inputDataLeft, const ArrayInDataRight &inputDataRight, const ECompEngine compEngine, const bool sumInto=false) |
| Contracts the point (and space) dimensions P (and D1 and D2) of two rank-2, 3, or 4 containers with dimensions (C,P), or (C,P,D1), or (C,P,D1,D2), respectively, and returns the result in a rank-1 container with dimensions (C). More... | |
| template<class Scalar , class ArrayOut , class ArrayDet , class ArrayWeights > | |
| static void | computeCellMeasure (ArrayOut &outVals, const ArrayDet &inDet, const ArrayWeights &inWeights) |
| Returns the weighted integration measures outVals with dimensions (C,P) used for the computation of cell integrals, by multiplying absolute values of the user-provided cell Jacobian determinants inDet with dimensions (C,P) with the user-provided integration weights inWeights with dimensions (P). More... | |
| template<class Scalar , class ArrayOut , class ArrayJac , class ArrayWeights > | |
| static void | computeFaceMeasure (ArrayOut &outVals, const ArrayJac &inJac, const ArrayWeights &inWeights, const int whichFace, const shards::CellTopology &parentCell) |
| Returns the weighted integration measures outVals with dimensions (C,P) used for the computation of face integrals, based on the provided cell Jacobian array inJac with dimensions (C,P,D,D) and the provided integration weights inWeights with dimensions (P). More... | |
| template<class Scalar , class ArrayOut , class ArrayJac , class ArrayWeights > | |
| static void | computeEdgeMeasure (ArrayOut &outVals, const ArrayJac &inJac, const ArrayWeights &inWeights, const int whichEdge, const shards::CellTopology &parentCell) |
| Returns the weighted integration measures outVals with dimensions (C,P) used for the computation of edge integrals, based on the provided cell Jacobian array inJac with dimensions (C,P,D,D) and the provided integration weights inWeights with dimensions (P). More... | |
| template<class Scalar , class ArrayTypeOut , class ArrayTypeMeasure , class ArrayTypeIn > | |
| static void | multiplyMeasure (ArrayTypeOut &outVals, const ArrayTypeMeasure &inMeasure, const ArrayTypeIn &inVals) |
| Multiplies fields inVals by weighted measures inMeasure and returns the field array outVals; this is a simple redirection to the call FunctionSpaceTools::scalarMultiplyDataField. More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | scalarMultiplyDataField (ArrayOutFields &outputFields, ArrayInData &inputData, ArrayInFields &inputFields, const bool reciprocal=false) |
| Scalar multiplication of data and fields; please read the description below. More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | scalarMultiplyDataData (ArrayOutData &outputData, ArrayInDataLeft &inputDataLeft, ArrayInDataRight &inputDataRight, const bool reciprocal=false) |
| Scalar multiplication of data and data; please read the description below. More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | dotMultiplyDataField (ArrayOutFields &outputFields, const ArrayInData &inputData, const ArrayInFields &inputFields) |
| Dot product of data and fields; please read the description below. More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | dotMultiplyDataData (ArrayOutData &outputData, const ArrayInDataLeft &inputDataLeft, const ArrayInDataRight &inputDataRight) |
| Dot product of data and data; please read the description below. More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | vectorMultiplyDataField (ArrayOutFields &outputFields, const ArrayInData &inputData, const ArrayInFields &inputFields) |
| Cross or outer product of data and fields; please read the description below. More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | vectorMultiplyDataData (ArrayOutData &outputData, const ArrayInDataLeft &inputDataLeft, const ArrayInDataRight &inputDataRight) |
| Cross or outer product of data and data; please read the description below. More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | tensorMultiplyDataField (ArrayOutFields &outputFields, const ArrayInData &inputData, const ArrayInFields &inputFields, const char transpose= 'N') |
| Matrix-vector or matrix-matrix product of data and fields; please read the description below. More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | tensorMultiplyDataData (ArrayOutData &outputData, const ArrayInDataLeft &inputDataLeft, const ArrayInDataRight &inputDataRight, const char transpose= 'N') |
| Matrix-vector or matrix-matrix product of data and data; please read the description below. More... | |
| template<class Scalar , class ArrayTypeInOut , class ArrayTypeSign > | |
| static void | applyLeftFieldSigns (ArrayTypeInOut &inoutOperator, const ArrayTypeSign &fieldSigns) |
| Applies left (row) signs, stored in the user-provided container fieldSigns and indexed by (C,L), to the operator inoutOperator indexed by (C,L,R). More... | |
| template<class Scalar , class ArrayTypeInOut , class ArrayTypeSign > | |
| static void | applyRightFieldSigns (ArrayTypeInOut &inoutOperator, const ArrayTypeSign &fieldSigns) |
| Applies right (column) signs, stored in the user-provided container fieldSigns and indexed by (C,R), to the operator inoutOperator indexed by (C,L,R). More... | |
| template<class Scalar , class ArrayTypeInOut , class ArrayTypeSign > | |
| static void | applyFieldSigns (ArrayTypeInOut &inoutFunction, const ArrayTypeSign &fieldSigns) |
| Applies field signs, stored in the user-provided container fieldSigns and indexed by (C,F), to the function inoutFunction indexed by (C,F), (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2). More... | |
| template<class Scalar , class ArrayOutPointVals , class ArrayInCoeffs , class ArrayInFields > | |
| static void | evaluate (ArrayOutPointVals &outPointVals, const ArrayInCoeffs &inCoeffs, const ArrayInFields &inFields) |
| Computes point values outPointVals of a discrete function specified by the basis inFields and coefficients inCoeffs. More... | |
Detailed Description
Defines expert-level interfaces for the evaluation of functions and operators in physical space (supported for FE, FV, and FD methods) and FE reference space; in addition, provides several function transformation utilities.
Definition at line 69 of file Intrepid_FunctionSpaceTools.hpp.
Member Function Documentation
|
static |
Applies field signs, stored in the user-provided container fieldSigns and indexed by (C,F), to the function inoutFunction indexed by (C,F), (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2).
Returns
![\[ \mbox{inoutFunction}(c,f,*) = \mbox{fieldSigns}(c,f)*\mbox{inoutFunction}(c,f,*) \]](form_278.png)
See Section Pullbacks for discussion of field signs.
- Parameters
-
inoutFunction [in/out] - Input / output function array. fieldSigns [in] - Right field signs.
Definition at line 1636 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Applies left (row) signs, stored in the user-provided container fieldSigns and indexed by (C,L), to the operator inoutOperator indexed by (C,L,R).
Mathematically, this method computes the matrix-matrix product
![\[ \mathbf{K}^{c} = \mbox{diag}(\sigma^c_0,\ldots,\sigma^c_{L-1}) \mathbf{K}^c \]](form_273.png)
where 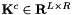 is array of matrices indexed by cell number c and stored in the rank-3 array inoutOperator, and
is array of matrices indexed by cell number c and stored in the rank-3 array inoutOperator, and 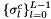 is array of left field signs indexed by cell number c and stored in the rank-2 container fieldSigns; see Section Pullbacks for discussion of field signs. This operation is required for operators generated by HCURL and HDIV-conforming vector-valued finite element basis functions; see Sections Pullbacks and Section Evaluation of finite element operators and functionals for applications of this method.
is array of left field signs indexed by cell number c and stored in the rank-2 container fieldSigns; see Section Pullbacks for discussion of field signs. This operation is required for operators generated by HCURL and HDIV-conforming vector-valued finite element basis functions; see Sections Pullbacks and Section Evaluation of finite element operators and functionals for applications of this method.
- Parameters
-
inoutOperator [in/out] - Input / output operator array. fieldSigns [in] - Left field signs.
Definition at line 1585 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Applies right (column) signs, stored in the user-provided container fieldSigns and indexed by (C,R), to the operator inoutOperator indexed by (C,L,R).
Mathematically, this method computes the matrix-matrix product
![\[ \mathbf{K}^{c} = \mathbf{K}^c \mbox{diag}(\sigma^c_0,\ldots,\sigma^c_{R-1}) \]](form_276.png)
where 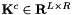 is array of matrices indexed by cell number c and stored in the rank-3 container inoutOperator, and
is array of matrices indexed by cell number c and stored in the rank-3 container inoutOperator, and 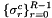 is array of right field signs indexed by cell number c and stored in the rank-2 container fieldSigns; see Section Pullbacks for discussion of field signs. This operation is required for operators generated by HCURL and HDIV-conforming vector-valued finite element basis functions; see Sections Pullbacks and Section Evaluation of finite element operators and functionals for applications of this method.
is array of right field signs indexed by cell number c and stored in the rank-2 container fieldSigns; see Section Pullbacks for discussion of field signs. This operation is required for operators generated by HCURL and HDIV-conforming vector-valued finite element basis functions; see Sections Pullbacks and Section Evaluation of finite element operators and functionals for applications of this method.
- Parameters
-
inoutOperator [in/out] - Input / output operator array. fieldSigns [in] - Right field signs.
Definition at line 1610 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
inlinestatic |
Returns the weighted integration measures outVals with dimensions (C,P) used for the computation of cell integrals, by multiplying absolute values of the user-provided cell Jacobian determinants inDet with dimensions (C,P) with the user-provided integration weights inWeights with dimensions (P).
Returns a rank-2 array (C, P) array such that
![\[ \mbox{outVals}(c,p) = |\mbox{det}(DF_{c}(\widehat{x}_p))|\omega_{p} \,, \]](form_265.png)
where 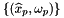 is a cubature rule defined on a reference cell (a set of integration points and their associated weights; see Intrepid::Cubature::getCubature for getting cubature rules on reference cells).
is a cubature rule defined on a reference cell (a set of integration points and their associated weights; see Intrepid::Cubature::getCubature for getting cubature rules on reference cells).
- Warning
- The user is responsible for providing input arrays with consistent data: the determinants in inDet should be evaluated at integration points on the reference cell corresponding to the weights in inWeights.
- Remarks
- See Intrepid::CellTools::setJacobian for computation of DF and Intrepid::CellTools::setJacobianDet for computation of its determinant.
- Parameters
-
outVals [out] - Output array with weighted cell measures. inDet [in] - Input array containing determinants of cell Jacobians. inWeights [in] - Input integration weights.
Definition at line 1337 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Returns the weighted integration measures outVals with dimensions (C,P) used for the computation of edge integrals, based on the provided cell Jacobian array inJac with dimensions (C,P,D,D) and the provided integration weights inWeights with dimensions (P).
Returns a rank-2 array (C, P) array such that
![\[ \mbox{outVals}(c,p) = \left\|\frac{d \Phi_c(\widehat{x}_p)}{d s}\right\|\omega_{p} \,, \]](form_270.png)
where:
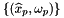 is a cubature rule defined on reference edge
is a cubature rule defined on reference edge 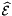 , with ordinal whichEdge relative to the specified parent reference cell;
, with ordinal whichEdge relative to the specified parent reference cell; 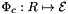 is parameterization of the physical edge corresponding to
is parameterization of the physical edge corresponding to 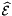 ; see Section Parametrization of physical 1- and 2-subcells.
; see Section Parametrization of physical 1- and 2-subcells.
- Warning
- The user is responsible for providing input arrays with consistent data: the Jacobians in inJac should be evaluated at integration points on the reference edge corresponding to the weights in inWeights.
- Remarks
- Cubature rules on reference edges are defined by a two-step process:
- A cubature rule is defined on the parametrization domain R = [-1,1] of the edge.
- The points are mapped to a reference edge using Intrepid::CellTools::mapToReferenceSubcell
- See Intrepid::CellTools::setJacobian for computation of DF and Intrepid::CellTools::setJacobianDet for computation of its determinant.
- Parameters
-
outVals [out] - Output array with weighted edge measures. inJac [in] - Input array containing cell Jacobians. inWeights [in] - Input integration weights. whichEdge [in] - Index of the edge subcell relative to the parent cell; defines the domain of integration. parentCell [in] - Parent cell topology.
Definition at line 1389 of file Intrepid_FunctionSpaceToolsDef.hpp.
References Intrepid::CellTools< Scalar >::getPhysicalEdgeTangents(), and Intrepid::RealSpaceTools< Scalar >::vectorNorm().
|
static |
Returns the weighted integration measures outVals with dimensions (C,P) used for the computation of face integrals, based on the provided cell Jacobian array inJac with dimensions (C,P,D,D) and the provided integration weights inWeights with dimensions (P).
Returns a rank-2 array (C, P) array such that
![\[ \mbox{outVals}(c,p) = \left\|\frac{\partial\Phi_c(\widehat{x}_p)}{\partial u}\times \frac{\partial\Phi_c(\widehat{x}_p)}{\partial v}\right\|\omega_{p} \,, \]](form_267.png)
where:
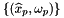 is a cubature rule defined on reference face
is a cubature rule defined on reference face 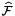 , with ordinal whichFace relative to the specified parent reference cell;
, with ordinal whichFace relative to the specified parent reference cell; 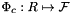 is parameterization of the physical face corresponding to
is parameterization of the physical face corresponding to 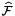 ; see Section Parametrization of physical 1- and 2-subcells.
; see Section Parametrization of physical 1- and 2-subcells.
- Warning
- The user is responsible for providing input arrays with consistent data: the Jacobians in inJac should be evaluated at integration points on the reference face corresponding to the weights in inWeights.
- Remarks
- Cubature rules on reference faces are defined by a two-step process:
- A cubature rule is defined on the parametrization domain R of the face (R is the standard 2-simplex {(0,0),(1,0),(0,1)} or the standard 2-cube [-1,1] X [-1,1]).
- The points are mapped to a reference face using Intrepid::CellTools::mapToReferenceSubcell
- See Intrepid::CellTools::setJacobian for computation of DF and Intrepid::CellTools::setJacobianDet for computation of its determinant.
- Parameters
-
outVals [out] - Output array with weighted face measures. inJac [in] - Input array containing cell Jacobians. inWeights [in] - Input integration weights. whichFace [in] - Index of the face subcell relative to the parent cell; defines the domain of integration. parentCell [in] - Parent cell topology.
Definition at line 1360 of file Intrepid_FunctionSpaceToolsDef.hpp.
References Intrepid::CellTools< Scalar >::getPhysicalFaceNormals(), and Intrepid::RealSpaceTools< Scalar >::vectorNorm().
|
static |
Contracts the point (and space) dimensions P (and D1 and D2) of two rank-2, 3, or 4 containers with dimensions (C,P), or (C,P,D1), or (C,P,D1,D2), respectively, and returns the result in a rank-1 container with dimensions (C).
- Parameters
-
outputData [out] - Output data array. inputDataLeft [in] - Left data input array. inputDataRight [in] - Right data input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE.
Definition at line 1307 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Dot product of data and data; please read the description below.
There are two use cases: \li dot product of a rank-2, 3 or 4 container \a <b>inputDataRight</b> with dimensions (C,P) (C,P,D1) or (C,P,D1,D2), representing the values of a scalar, vector or a tensor set of data, by the values in a rank-2, 3 or 4 container \a <b>inputDataLeft</b> indexed by (C,P), (C,P,D1), or (C,P,D1,D2) representing the values of scalar, vector or tensor data, OR \li dot product of a rank-2, 3 or 4 container \a <b>inputDataRight</b> with dimensions (P), (P,D1) or (P,D1,D2), representing the values of scalar, vector or tensor data, by the values in a rank-2 container \a <b>inputDataLeft</b> indexed by (C,P), (C,P,D1) or (C,P,D1,D2), representing the values of scalar, vector, or tensor data; the output value container \a <b>outputData</b> is indexed by (C,P), regardless of which of the two use cases is considered. For input fields containers without a dimension index, this operation reduces to scalar multiplication.
- Parameters
-
outputData [out] - Output (dot product) data array. inputDataLeft [in] - Left input data array. inputDataRight [in] - Right input data array.
Definition at line 1461 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Dot product of data and fields; please read the description below.
There are two use cases: \li dot product of a rank-3, 4 or 5 container \a <b>inputFields</b> with dimensions (C,F,P) (C,F,P,D1) or (C,F,P,D1,D2), representing the values of a set of scalar, vector or tensor fields, by the values in a rank-2, 3 or 4 container \a <b>inputData</b> indexed by (C,P), (C,P,D1), or (C,P,D1,D2) representing the values of scalar, vector or tensor data, OR \li dot product of a rank-2, 3 or 4 container \a <b>inputFields</b> with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or tensor field, by the values in a rank-2 container \a <b>inputData</b> indexed by (C,P), (C,P,D1) or (C,P,D1,D2), representing the values of scalar, vector or tensor data; the output value container \a <b>outputFields</b> is indexed by (C,F,P), regardless of which of the two use cases is considered. For input fields containers without a dimension index, this operation reduces to scalar multiplication.
- Parameters
-
outputFields [out] - Output (dot product) fields array. inputData [in] - Data array. inputFields [in] - Input fields array.
Definition at line 1451 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Computes point values outPointVals of a discrete function specified by the basis inFields and coefficients inCoeffs.
The array \a <b>inFields</b> with dimensions (C,F,P), (C,F,P,D1), or (C,F,P,D1,D2) represents the signed, transformed field (basis) values at points in REFERENCE frame; the \a <b>outPointVals</b> array with dimensions (C,P), (C,P,D1), or (C,P,D1,D2), respectively, represents values of a discrete function at points in PHYSICAL frame. The array \a <b>inCoeffs</b> dimensioned (C,F) supplies the coefficients for the field (basis) array. Returns rank-2,3 or 4 array such that
![\[ outPointValues(c,p,*) = \sum_{f=0}^{F-1} \sigma_{c,f} u_{c,f}(x_p) \]](form_279.png)
where 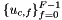 is scalar, vector or tensor valued finite element basis defined on physical cell
is scalar, vector or tensor valued finite element basis defined on physical cell 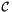 and
and 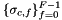 are the field signs of the basis functions; see Section Pullbacks. This method implements the last step in a four step process; please see Section Evaluation of finite element fields for details about the first three steps that prepare the necessary data for this method.
are the field signs of the basis functions; see Section Pullbacks. This method implements the last step in a four step process; please see Section Evaluation of finite element fields for details about the first three steps that prepare the necessary data for this method.
- Parameters
-
outPointVals [out] - Output point values of a discrete function. inCoeffs [in] - Coefficients associated with the fields (basis) array. inFields [in] - Field (basis) values.
Definition at line 1729 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Contracts the point (and space) dimensions P (and D1 and D2) of a rank-3, 4, or 5 container and a rank-2, 3, or 4 container, respectively, with dimensions (C,F,P) and (C,P), or (C,F,P,D1) and (C,P,D1), or (C,F,P,D1,D2) and (C,P,D1,D2), respectively, and returns the result in a rank-2 container with dimensions (C,F).
For a fixed index "C", (C,F) represents a (column) vector of length F.
- Parameters
-
outputFields [out] - Output fields array. inputData [in] - Data array. inputFields [in] - Input fields array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE.
Definition at line 1277 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a curl field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P,D), into the output container outVals, defined on cells in physical space and indexed by (C,F,P,D).
Computes pullback of curls of \e HCURL functions
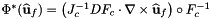 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_243.png)
In this case 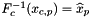 and the user-provided container should contain the curls of the vector function set
and the user-provided container should contain the curls of the vector function set 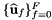 at the reference points:
at the reference points:
![\[ inVals(f,p,*) = \nabla\times\widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_256.png)
The method returns
![\[ outVals(c,f,p,*) = \left(J^{-1}_{c} DF_{c}\cdot\nabla\times\widehat{\bf u}_f\right)\circ F^{-1}_{c}(x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) DF_{c}(\widehat{x}_p)\cdot\nabla\times\widehat{\bf u}_f(\widehat{x}_p) \qquad 0\le c < C \,. \]](form_257.png)
See Section Pullbacks for more details about pullbacks.
Definition at line 81 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a (vector) value field in the H-curl space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P,D), into the output container outVals, defined on cells in physical space and indexed by (C,F,P,D).
Computes pullback of \e HCURL functions
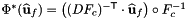 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_243.png)
In this case 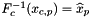 and the user-provided container should contain the values of the vector function set
and the user-provided container should contain the values of the vector function set 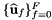 at the reference points:
at the reference points:
![\[ inVals(f,p,*) = \widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_253.png)
The method returns
![\[ outVals(c,f,p,*) = \left((DF_c)^{-{\sf T}}\cdot\widehat{\bf u}_f\right)\circ F^{-1}_{c}(x_{c,p}) = (DF_c)^{-{\sf T}}(\widehat{x}_p)\cdot\widehat{\bf u}_f(\widehat{x}_p) \qquad 0\le c < C \,. \]](form_254.png)
See Section Pullbacks for more details about pullbacks.
Definition at line 71 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a divergence field in the H-div space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P), into the output container outVals, defined on cells in physical space and indexed by (C,F,P).
Computes pullback of the divergence of \e HDIV functions
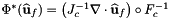 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_243.png)
In this case 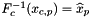 and the user-provided container should contain the divergencies of the vector function set
and the user-provided container should contain the divergencies of the vector function set 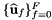 at the reference points:
at the reference points:
![\[ inVals(f,p) = \nabla\cdot\widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_261.png)
The method returns
![\[ outVals(c,f,p,*) = \left(J^{-1}_{c}\nabla\cdot\widehat{\bf u}_{f}\right) \circ F^{-1}_{c} (x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) \nabla\cdot\widehat{\bf u}_{f} (\widehat{x}_p) \qquad 0\le c < C \,. \]](form_262.png)
See Section Pullbacks for more details about pullbacks.
Definition at line 105 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a (vector) value field in the H-div space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P,D), into the output container outVals, defined on cells in physical space and indexed by (C,F,P,D).
Computes pullback of \e HDIV functions
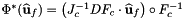 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_243.png)
In this case 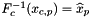 and the user-provided container should contain the values of the vector function set
and the user-provided container should contain the values of the vector function set 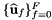 at the reference points:
at the reference points:
![\[ inVals(f,p,*) = \widehat{\bf u}_f(\widehat{x}_p) \,. \]](form_253.png)
The method returns
![\[ outVals(c,f,p,*) = \left(J^{-1}_{c} DF_{c}\cdot \widehat{\bf u}_f\right)\circ F^{-1}_{c}(x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) DF_{c}(\widehat{x}_p)\cdot\widehat{\bf u}_f(\widehat{x}_p) \qquad 0\le c < C \,. \]](form_259.png)
See Section Pullbacks for more details about pullbacks.
Definition at line 93 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a gradient field in the H-grad space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P,D), into the output container outVals, defined on cells in physical space and indexed by (C,F,P,D).
Computes pullback of gradients of \e HGRAD functions
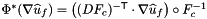 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_243.png)
In this case 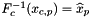 and the user-provided container should contain the gradients of the function set
and the user-provided container should contain the gradients of the function set 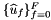 at the reference points:
at the reference points:
![\[ inVals(f,p,*) = \nabla\widehat{u}_f(\widehat{x}_p) \,. \]](form_249.png)
The method returns
![\[ outVals(c,f,p,*) = \left((DF_c)^{-{\sf T}}\cdot\nabla\widehat{u}_f\right)\circ F^{-1}_{c}(x_{c,p}) = (DF_c)^{-{\sf T}}(\widehat{x}_p)\cdot\nabla\widehat{u}_f(\widehat{x}_p) \qquad 0\le c < C \,. \]](form_250.png)
See Section Pullbacks for more details about pullbacks.
Definition at line 61 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a (scalar) value field in the H-grad space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P), into the output container outVals, defined on cells in physical space and indexed by (C,F,P).
Computes pullback of \e HGRAD functions \form#242
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_243.png)
In this case 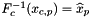 and the user-provided container should contain the values of the function set
and the user-provided container should contain the values of the function set 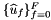 at the reference points:
at the reference points:
![\[ inVals(f,p) = \widehat{u}_f(\widehat{x}_p) \,. \]](form_246.png)
The method returns
![\[ outVals(c,f,p) = \widehat{u}_f\circ F^{-1}_{c}(x_{c,p}) = \widehat{u}_f(\widehat{x}_p) = inVals(f,p) \qquad 0\le c < C \,, \]](form_247.png)
i.e., it simply replicates the values in the user-provided container to every cell. See Section Pullbacks for more details about pullbacks.
Definition at line 53 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Transformation of a (scalar) value field in the H-vol space, defined at points on a reference cell, stored in the user-provided container inVals and indexed by (F,P), into the output container outVals, defined on cells in physical space and indexed by (C,F,P).
Computes pullback of \e HVOL functions
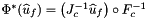 for points in one or more physical cells that are images of a given set of points in the reference cell:
for points in one or more physical cells that are images of a given set of points in the reference cell:
![\[ \{ x_{c,p} \}_{p=0}^P = \{ F_{c} (\widehat{x}_p) \}_{p=0}^{P}\qquad 0\le c < C \,. \]](form_243.png)
In this case 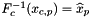 and the user-provided container should contain the values of the functions in the set
and the user-provided container should contain the values of the functions in the set 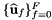 at the reference points:
at the reference points:
![\[ inVals(f,p) = \widehat{u}_f(\widehat{x}_p) \,. \]](form_246.png)
The method returns
![\[ outVals(c,f,p,*) = \left(J^{-1}_{c}\widehat{u}_{f}\right) \circ F^{-1}_{c} (x_{c,p}) = J^{-1}_{c}(\widehat{x}_p) \widehat{u}_{f} (\widehat{x}_p) \qquad 0\le c < C \,. \]](form_264.png)
See Section Pullbacks for more details about pullbacks.
Definition at line 114 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Contracts leftValues and rightValues arrays on the point and possibly space dimensions and stores the result in outputValues; this is a generic, high-level integration routine that calls either FunctionSpaceTools::operatorIntegral, or FunctionSpaceTools::functionalIntegral, or FunctionSpaceTools::dataIntegral methods, depending on the rank of the outputValues array.
- Parameters
-
outputValues [out] - Output array. leftValues [in] - Left input array. rightValues [in] - Right input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE.
Definition at line 122 of file Intrepid_FunctionSpaceToolsDef.hpp.
References Intrepid::FieldContainer< Scalar, ArrayTypeId >::dimension(), and Intrepid::FieldContainer< Scalar, ArrayTypeId >::rank().
|
static |
Multiplies fields inVals by weighted measures inMeasure and returns the field array outVals; this is a simple redirection to the call FunctionSpaceTools::scalarMultiplyDataField.
- Parameters
-
outVals [out] - Output array with scaled field values. inMeasure [in] - Input array containing weighted measures. inVals [in] - Input fields.
Definition at line 1419 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Contracts the point (and space) dimensions P (and D1 and D2) of two rank-3, 4, or 5 containers with dimensions (C,L,P) and (C,R,P), or (C,L,P,D1) and (C,R,P,D1), or (C,L,P,D1,D2) and (C,R,P,D1,D2), and returns the result in a rank-3 container with dimensions (C,L,R).
For a fixed index "C", (C,L,R) represents a rectangular L X R matrix
where L and R may be different.
- Parameters
-
outputFields [out] - Output array. leftFields [in] - Left input array. rightFields [in] - Right input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE.
Definition at line 1246 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Scalar multiplication of data and data; please read the description below.
There are two use cases: \li multiplies a rank-2, 3, or 4 container \a <b>inputDataRight</b> with dimensions (C,P), (C,P,D1) or (C,P,D1,D2), representing the values of a set of scalar, vector or tensor data, by the values in a rank-2 container \a <b>inputDataLeft</b> indexed by (C,P), representing the values of scalar data, OR \li multiplies a rank-1, 2, or 3 container \a <b>inputDataRight</b> with dimensions (P), (P,D1) or (P,D1,D2), representing the values of scalar, vector or tensor data, by the values in a rank-2 container \a <b>inputDataLeft</b> indexed by (C,P), representing the values of scalar data; the output value container \a <b>outputData</b> is indexed by (C,P), (C,P,D1) or (C,P,D1,D2), regardless of which of the two use cases is considered.
- Note
- The arguments inputDataLeft, inputDataRight can be changed! This enables in-place multiplication.
- Parameters
-
outputData [out] - Output data array. inputDataLeft [in] - Left (multiplying) data array. inputDataRight [in] - Right (being multiplied) data array. reciprocal [in] - If TRUE, divides input fields by the data (instead of multiplying). Default: FALSE.
Definition at line 1440 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Scalar multiplication of data and fields; please read the description below.
There are two use cases: \li multiplies a rank-3, 4, or 5 container \a <b>inputFields</b> with dimensions (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2), representing the values of a set of scalar, vector or tensor fields, by the values in a rank-2 container \a <b>inputData</b> indexed by (C,P), representing the values of scalar data, OR \li multiplies a rank-2, 3, or 4 container \a <b>inputFields</b> with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or a tensor field, by the values in a rank-2 container \a <b>inputData</b> indexed by (C,P), representing the values of scalar data; the output value container \a <b>outputFields</b> is indexed by (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2), regardless of which of the two use cases is considered.
- Note
- The argument inputFields can be changed! This enables in-place multiplication.
- Parameters
-
outputFields [out] - Output (product) fields array. inputData [in] - Data (multiplying) array. inputFields [in] - Input (being multiplied) fields array. reciprocal [in] - If TRUE, divides input fields by the data (instead of multiplying). Default: FALSE.
Definition at line 1429 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Matrix-vector or matrix-matrix product of data and data; please read the description below.
There are four use cases: \li matrix-vector product of a rank-3 container \a <b>inputDataRight</b> with dimensions (C,P,D), representing the values of a set of vector data, on the left by the values in a rank-2, 3, or 4 container \a <b>inputDataLeft</b> indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data, OR \li matrix-vector product of a rank-2 container \a <b>inputDataRight</b> with dimensions (P,D), representing the values of vector data, on the left by the values in a rank-2, 3, or 4 container \a <b>inputDataLeft</b> indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data, OR \li matrix-matrix product of a rank-4 container \a <b>inputDataRight</b> with dimensions (C,P,D,D), representing the values of a set of tensor data, on the left by the values in a rank-2, 3, or 4 container \a <b>inputDataLeft</b> indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data, OR \li matrix-matrix product of a rank-3 container \a <b>inputDataRight</b> with dimensions (P,D,D), representing the values of tensor data, on the left by the values in a rank-2, 3, or 4 container \a <b>inputDataLeft</b> indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data; for matrix-vector products, the output value container \a <b>outputData</b> is indexed by (C,P,D); for matrix-matrix products, the output value container \a <b>outputData</b> is indexed by (C,P,D1,D2).
- Remarks
- The rank of inputDataLeft implicitly defines the type of tensor data:
- rank = 2 corresponds to a constant diagonal tensor
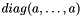
- rank = 3 corresponds to a nonconstant diagonal tensor
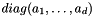
- rank = 4 corresponds to a full tensor
- rank = 2 corresponds to a constant diagonal tensor
- Note
- It is assumed that all tensors are square!
- The method is defined for spatial dimensions D = 1, 2, 3
- Parameters
-
outputData [out] - Output (matrix-vector product) data array. inputDataLeft [in] - Left input data array. inputDataRight [in] - Right input data array. transpose [in] - If 'T', use transposed tensor; if 'N', no transpose. Default: 'N'.
Definition at line 1577 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Matrix-vector or matrix-matrix product of data and fields; please read the description below.
There are four use cases: \li matrix-vector product of a rank-4 container \a <b>inputFields</b> with dimensions (C,F,P,D), representing the values of a set of vector fields, on the left by the values in a rank-2, 3, or 4 container \a <b>inputData</b> indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data, OR \li matrix-vector product of a rank-3 container \a <b>inputFields</b> with dimensions (F,P,D), representing the values of a vector field, on the left by the values in a rank-2, 3, or 4 container \a <b>inputData</b> indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data, OR \li matrix-matrix product of a rank-5 container \a <b>inputFields</b> with dimensions (C,F,P,D,D), representing the values of a set of tensor fields, on the left by the values in a rank-2, 3, or 4 container \a <b>inputData</b> indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data, OR \li matrix-matrix product of a rank-4 container \a <b>inputFields</b> with dimensions (F,P,D,D), representing the values of a tensor field, on the left by the values in a rank-2, 3, or 4 container \a <b>inputData</b> indexed by (C,P), (C,P,D) or (C,P,D,D), respectively, representing the values of tensor data; for matrix-vector products, the output value container \a <b>outputFields</b> is indexed by (C,F,P,D); for matrix-matrix products the output value container \a <b>outputFields</b> is indexed by (C,F,P,D,D).
- Remarks
- The rank of inputData implicitly defines the type of tensor data:
- rank = 2 corresponds to a constant diagonal tensor
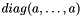
- rank = 3 corresponds to a nonconstant diagonal tensor
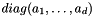
- rank = 4 corresponds to a full tensor
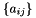
- rank = 2 corresponds to a constant diagonal tensor
- Note
- It is assumed that all tensors are square!
- The method is defined for spatial dimensions D = 1, 2, 3
- Parameters
-
outputFields [out] - Output (matrix-vector or matrix-matrix product) fields array. inputData [in] - Data array. inputFields [in] - Input fields array. transpose [in] - If 'T', use transposed left data tensor; if 'N', no transpose. Default: 'N'.
Definition at line 1517 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Cross or outer product of data and data; please read the description below.
There are four use cases: \li cross product of a rank-3 container \a <b>inputDataRight</b> with dimensions (C,P,D), representing the values of a set of vector data, on the left by the values in a rank-3 container \a <b>inputDataLeft</b> indexed by (C,P,D) representing the values of vector data, OR \li cross product of a rank-2 container \a <b>inputDataRight</b> with dimensions (P,D), representing the values of vector data, on the left by the values in a rank-3 container \a <b>inputDataLeft</b> indexed by (C,P,D), representing the values of vector data, OR \li outer product of a rank-3 container \a <b>inputDataRight</b> with dimensions (C,P,D), representing the values of a set of vector data, on the left by the values in a rank-3 container \a <b>inputDataLeft</b> indexed by (C,P,D) representing the values of vector data, OR \li outer product of a rank-2 container \a <b>inputDataRight</b> with dimensions (P,D), representing the values of vector data, on the left by the values in a rank-3 container \a <b>inputDataLeft</b> indexed by (C,P,D), representing the values of vector data; for cross products, the output value container \a <b>outputData</b> is indexed by (C,P,D) in 3D (vector output) and by (C,P) in 2D (scalar output); for outer products, the output value container \a <b>outputData</b> is indexed by (C,P,D,D).
- Parameters
-
outputData [out] - Output (cross or outer product) data array. inputDataLeft [in] - Left input data array. inputDataRight [in] - Right input data array.
Definition at line 1494 of file Intrepid_FunctionSpaceToolsDef.hpp.
|
static |
Cross or outer product of data and fields; please read the description below.
There are four use cases: \li cross product of a rank-4 container \a <b>inputFields</b> with dimensions (C,F,P,D), representing the values of a set of vector fields, on the left by the values in a rank-3 container \a <b>inputData</b> indexed by (C,P,D), representing the values of vector data, OR \li cross product of a rank-3 container \a <b>inputFields</b> with dimensions (F,P,D), representing the values of a vector field, on the left by the values in a rank-3 container \a <b>inputData</b> indexed by (C,P,D), representing the values of vector data, OR \li outer product of a rank-4 container \a <b>inputFields</b> with dimensions (C,F,P,D), representing the values of a set of vector fields, on the left by the values in a rank-3 container \a <b>inputData</b> indexed by (C,P,D), representing the values of vector data, OR \li outer product of a rank-3 container \a <b>inputFields</b> with dimensions (F,P,D), representing the values of a vector field, on the left by the values in a rank-3 container \a <b>inputData</b> indexed by (C,P,D), representing the values of vector data; for cross products, the output value container \a <b>outputFields</b> is indexed by (C,F,P,D) in 3D (vector output) and by (C,F,P) in 2D (scalar output); for outer products, the output value container \a <b>outputFields</b> is indexed by (C,F,P,D,D).
- Parameters
-
outputFields [out] - Output (cross or outer product) fields array. inputData [in] - Data array. inputFields [in] - Input fields array.
Definition at line 1471 of file Intrepid_FunctionSpaceToolsDef.hpp.
The documentation for this class was generated from the following files:
- http://docs.trilinos.org/r13.0/packages/intrepid/src/Discretization/FunctionSpaceTools/Intrepid_FunctionSpaceTools.hpp
- http://docs.trilinos.org/r13.0/packages/intrepid/src/Discretization/FunctionSpaceTools/Intrepid_FunctionSpaceToolsDef.hpp
 1.8.5
1.8.5