A stateless class for operations on cell data. Provides methods for: More...
#include <Intrepid_CellTools.hpp>
Classes | |
| struct | mapToPhysicalFrameTempSpec |
| Computes F, the reference-to-physical frame map. More... | |
| struct | setJacobianTempSpec |
| Computes the Jacobian matrix DF of the reference-to-physical frame map F. More... | |
Public Member Functions | |
| CellTools () | |
| Default constructor. | |
| ~CellTools () | |
| Destructor. | |
Static Public Member Functions | |
| template<class ArrayJac , class ArrayPoint , class ArrayCell > | |
| static void | setJacobian (ArrayJac &jacobian, const ArrayPoint &points, const ArrayCell &cellWorkset, const shards::CellTopology &cellTopo, const int &whichCell=-1) |
| template<class ArrayJac , class ArrayPoint , class ArrayCell > | |
| static void | setJacobian (ArrayJac &jacobian, const ArrayPoint &points, const ArrayCell &cellWorkset, const Teuchos::RCP< Basis< Scalar, FieldContainer< Scalar > > > HGRAD_Basis, const int &whichCell=-1) |
| template<class ArrayJacInv , class ArrayJac > | |
| static void | setJacobianInv (ArrayJacInv &jacobianInv, const ArrayJac &jacobian) |
| Computes the inverse of the Jacobian matrix DF of the reference-to-physical frame map F. More... | |
| template<class ArrayJacDet , class ArrayJac > | |
| static void | setJacobianDet (ArrayJacDet &jacobianDet, const ArrayJac &jacobian) |
| Computes the determinant of the Jacobian matrix DF of the reference-to-physical frame map F. More... | |
| template<class ArrayPhysPoint , class ArrayRefPoint , class ArrayCell > | |
| static void | mapToPhysicalFrame (ArrayPhysPoint &physPoints, const ArrayRefPoint &refPoints, const ArrayCell &cellWorkset, const shards::CellTopology &cellTopo, const int &whichCell=-1) |
| Computes F, the reference-to-physical frame map. More... | |
| template<class ArrayPhysPoint , class ArrayRefPoint , class ArrayCell > | |
| static void | mapToPhysicalFrame (ArrayPhysPoint &physPoints, const ArrayRefPoint &refPoints, const ArrayCell &cellWorkset, const Teuchos::RCP< Basis< Scalar, FieldContainer< Scalar > > > HGRAD_Basis, const int &whichCell=-1) |
| template<class ArrayRefPoint , class ArrayPhysPoint , class ArrayCell > | |
| static void | mapToReferenceFrame (ArrayRefPoint &refPoints, const ArrayPhysPoint &physPoints, const ArrayCell &cellWorkset, const shards::CellTopology &cellTopo, const int &whichCell=-1) |
Computes 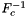 , the inverse of the reference-to-physical frame map using a default initial guess. More... , the inverse of the reference-to-physical frame map using a default initial guess. More... | |
| template<class ArrayRefPoint , class ArrayPhysPoint , class ArrayCell > | |
| static void | mapToReferenceFrame (ArrayRefPoint &refPoints, const ArrayPhysPoint &physPoints, const ArrayCell &cellWorkset, const Teuchos::RCP< Basis< Scalar, FieldContainer< Scalar > > > HGRAD_Basis, const int &whichCell=-1) |
| template<class ArrayRefPoint , class ArrayInitGuess , class ArrayPhysPoint , class ArrayCell > | |
| static void | mapToReferenceFrameInitGuess (ArrayRefPoint &refPoints, const ArrayInitGuess &initGuess, const ArrayPhysPoint &physPoints, const ArrayCell &cellWorkset, const shards::CellTopology &cellTopo, const int &whichCell=-1) |
Computation of 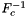 , the inverse of the reference-to-physical frame map using user-supplied initial guess. More... , the inverse of the reference-to-physical frame map using user-supplied initial guess. More... | |
| template<class ArrayRefPoint , class ArrayInitGuess , class ArrayPhysPoint , class ArrayCell > | |
| static void | mapToReferenceFrameInitGuess (ArrayRefPoint &refPoints, const ArrayInitGuess &initGuess, const ArrayPhysPoint &physPoints, const ArrayCell &cellWorkset, const Teuchos::RCP< Basis< Scalar, FieldContainer< Scalar > > > HGRAD_Basis, const int &whichCell=-1) |
| template<class ArraySubcellPoint , class ArrayParamPoint > | |
| static void | mapToReferenceSubcell (ArraySubcellPoint &refSubcellPoints, const ArrayParamPoint ¶mPoints, const int subcellDim, const int subcellOrd, const shards::CellTopology &parentCell) |
| Computes parameterization maps of 1- and 2-subcells of reference cells. More... | |
| template<class ArrayEdgeTangent > | |
| static void | getReferenceEdgeTangent (ArrayEdgeTangent &refEdgeTangent, const int &edgeOrd, const shards::CellTopology &parentCell) |
| Computes constant tangent vectors to edges of 2D or 3D reference cells. More... | |
| template<class ArrayFaceTangentU , class ArrayFaceTangentV > | |
| static void | getReferenceFaceTangents (ArrayFaceTangentU &refFaceTanU, ArrayFaceTangentV &refFaceTanV, const int &faceOrd, const shards::CellTopology &parentCell) |
| Computes pairs of constant tangent vectors to faces of a 3D reference cells. More... | |
| template<class ArraySideNormal > | |
| static void | getReferenceSideNormal (ArraySideNormal &refSideNormal, const int &sideOrd, const shards::CellTopology &parentCell) |
| Computes constant normal vectors to sides of 2D or 3D reference cells. More... | |
| template<class ArrayFaceNormal > | |
| static void | getReferenceFaceNormal (ArrayFaceNormal &refFaceNormal, const int &faceOrd, const shards::CellTopology &parentCell) |
| Computes constant normal vectors to faces of 3D reference cell. More... | |
| template<class ArrayEdgeTangent , class ArrayJac > | |
| static void | getPhysicalEdgeTangents (ArrayEdgeTangent &edgeTangents, const ArrayJac &worksetJacobians, const int &worksetEdgeOrd, const shards::CellTopology &parentCell) |
Computes non-normalized tangent vectors to physical edges in an edge workset 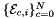 ; (see Subcell worksets for definition of edge worksets). More... ; (see Subcell worksets for definition of edge worksets). More... | |
| template<class ArrayFaceTangentU , class ArrayFaceTangentV , class ArrayJac > | |
| static void | getPhysicalFaceTangents (ArrayFaceTangentU &faceTanU, ArrayFaceTangentV &faceTanV, const ArrayJac &worksetJacobians, const int &worksetFaceOrd, const shards::CellTopology &parentCell) |
Computes non-normalized tangent vector pairs to physical faces in a face workset 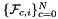 ; (see Subcell worksets for definition of face worksets). More... ; (see Subcell worksets for definition of face worksets). More... | |
| template<class ArraySideNormal , class ArrayJac > | |
| static void | getPhysicalSideNormals (ArraySideNormal &sideNormals, const ArrayJac &worksetJacobians, const int &worksetSideOrd, const shards::CellTopology &parentCell) |
Computes non-normalized normal vectors to physical sides in a side workset 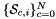 . More... . More... | |
| template<class ArrayFaceNormal , class ArrayJac > | |
| static void | getPhysicalFaceNormals (ArrayFaceNormal &faceNormals, const ArrayJac &worksetJacobians, const int &worksetFaceOrd, const shards::CellTopology &parentCell) |
Computes non-normalized normal vectors to physical faces in a face workset 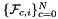 ; (see Subcell worksets for definition of face worksets). More... ; (see Subcell worksets for definition of face worksets). More... | |
| static int | checkPointInclusion (const Scalar *point, const int pointDim, const shards::CellTopology &cellTopo, const double &threshold=INTREPID_THRESHOLD) |
| Checks if a point belongs to a reference cell. More... | |
| template<class ArrayPoint > | |
| static int | checkPointsetInclusion (const ArrayPoint &points, const shards::CellTopology &cellTopo, const double &threshold=INTREPID_THRESHOLD) |
| Checks if a set of points belongs to a reference cell. More... | |
| template<class ArrayIncl , class ArrayPoint > | |
| static void | checkPointwiseInclusion (ArrayIncl &inRefCell, const ArrayPoint &points, const shards::CellTopology &cellTopo, const double &threshold=INTREPID_THRESHOLD) |
| Checks every point in a set for inclusion in a reference cell. More... | |
| template<class ArrayIncl , class ArrayPoint , class ArrayCell > | |
| static void | checkPointwiseInclusion (ArrayIncl &inCell, const ArrayPoint &points, const ArrayCell &cellWorkset, const shards::CellTopology &cell, const int &whichCell=-1, const double &threshold=INTREPID_THRESHOLD) |
| Checks every point in a set or multiple sets for inclusion in physical cells from a cell workset. More... | |
| static const double * | getReferenceVertex (const shards::CellTopology &cell, const int vertexOrd) |
| Retrieves the Cartesian coordinates of a reference cell vertex. More... | |
| template<class ArraySubcellVert > | |
| static void | getReferenceSubcellVertices (ArraySubcellVert &subcellVertices, const int subcellDim, const int subcellOrd, const shards::CellTopology &parentCell) |
| Retrieves the Cartesian coordinates of all vertices of a reference subcell. More... | |
| static const double * | getReferenceNode (const shards::CellTopology &cell, const int nodeOrd) |
| Retrieves the Cartesian coordinates of a reference cell node. More... | |
| template<class ArraySubcellNode > | |
| static void | getReferenceSubcellNodes (ArraySubcellNode &subcellNodes, const int subcellDim, const int subcellOrd, const shards::CellTopology &parentCell) |
| Retrieves the Cartesian coordinates of all nodes of a reference subcell. More... | |
| static int | hasReferenceCell (const shards::CellTopology &cellTopo) |
| Checks if a cell topology has reference cell. More... | |
| static void | printSubcellVertices (const int subcellDim, const int subcellOrd, const shards::CellTopology &parentCell) |
| Prints the reference space coordinates of the vertices of the specified subcell. More... | |
| template<class ArrayCell > | |
| static void | printWorksetSubcell (const ArrayCell &cellWorkset, const shards::CellTopology &parentCell, const int &pCellOrd, const int &subcellDim, const int &subcellOrd, const int &fieldWidth=3) |
| Prints the nodes of a subcell from a cell workset. More... | |
| template<class ArrayCVCoord , class ArrayCellCoord > | |
| static void | getSubCVCoords (ArrayCVCoord &subCVcoords, const ArrayCellCoord &cellCoords, const shards::CellTopology &primaryCell) |
| Computes coordinates of sub-control volumes in each primary cell. More... | |
| template<class ArrayCent , class ArrayCellCoord > | |
| static void | getBarycenter (ArrayCent &barycenter, const ArrayCellCoord &cellCoords) |
| Compute cell barycenters. More... | |
Static Private Member Functions | |
| static const FieldContainer < double > & | getSubcellParametrization (const int subcellDim, const shards::CellTopology &parentCell) |
| Returns array with the coefficients of the parametrization maps for the edges or faces of a reference cell topology. More... | |
| static void | setSubcellParametrization (FieldContainer< double > &subcellParametrization, const int subcellDim, const shards::CellTopology &parentCell) |
| Defines orientation-preserving parametrizations of reference edges and faces of cell topologies with reference cells. More... | |
| template<class ArrayJac , class ArrayPoint , class ArrayCell > | |
| static void | validateArguments_setJacobian (const ArrayJac &jacobian, const ArrayPoint &points, const ArrayCell &cellWorkset, const int &whichCell, const shards::CellTopology &cellTopo) |
| Validates arguments to Intrepid::CellTools::setJacobian. More... | |
| template<class ArrayJacInv , class ArrayJac > | |
| static void | validateArguments_setJacobianInv (const ArrayJacInv &jacobianInv, const ArrayJac &jacobian) |
| Validates arguments to Intrepid::CellTools::setJacobianInv. More... | |
| template<class ArrayJacDet , class ArrayJac > | |
| static void | validateArguments_setJacobianDetArgs (const ArrayJacDet &jacobianDet, const ArrayJac &jacobian) |
| Validates arguments to Intrepid::CellTools::setJacobianDet. More... | |
| template<class ArrayPhysPoint , class ArrayRefPoint , class ArrayCell > | |
| static void | validateArguments_mapToPhysicalFrame (const ArrayPhysPoint &physPoints, const ArrayRefPoint &refPoints, const ArrayCell &cellWorkset, const shards::CellTopology &cellTopo, const int &whichCell) |
| Validates arguments to Intrepid::CellTools::mapToPhysicalFrame. More... | |
| template<class ArrayRefPoint , class ArrayPhysPoint , class ArrayCell > | |
| static void | validateArguments_mapToReferenceFrame (const ArrayRefPoint &refPoints, const ArrayPhysPoint &physPoints, const ArrayCell &cellWorkset, const shards::CellTopology &cellTopo, const int &whichCell) |
| Validates arguments to Intrepid::CellTools::mapToReferenceFrame with default initial guess. More... | |
| template<class ArrayRefPoint , class ArrayInitGuess , class ArrayPhysPoint , class ArrayCell > | |
| static void | validateArguments_mapToReferenceFrame (const ArrayRefPoint &refPoints, const ArrayInitGuess &initGuess, const ArrayPhysPoint &physPoints, const ArrayCell &cellWorkset, const shards::CellTopology &cellTopo, const int &whichCell) |
| Validates arguments to Intrepid::CellTools::mapToReferenceFrame with user-defined initial guess. More... | |
| template<class ArrayIncl , class ArrayPoint , class ArrayCell > | |
| static void | validateArguments_checkPointwiseInclusion (ArrayIncl &inCell, const ArrayPoint &physPoints, const ArrayCell &cellWorkset, const int &whichCell, const shards::CellTopology &cell) |
| Validates arguments to Intrepid::CellTools::checkPointwiseInclusion. More... | |
Detailed Description
template<class Scalar>
class Intrepid::CellTools< Scalar >
A stateless class for operations on cell data. Provides methods for:
- computing Jacobians of reference-to-physical frame mappings, their inverses and determinants
- application of the reference-to-physical frame mapping and its inverse
- parametrizations of edges and faces of reference cells needed for edge and face integrals,
- computation of edge and face tangents and face normals on both reference and physical frames
- inclusion tests for point sets in reference and physical cells.
Definition at line 109 of file Intrepid_CellTools.hpp.
Member Function Documentation
|
static |
Checks if a point belongs to a reference cell.
Requires cell topology with a reference cell.
- Parameters
-
point [in] - spatial coordinates of the point tested for inclusion pointDim [in] - spatial dimension of that point cellTopo [in] - cell topology of the cells stored in cellWorksetthreshold [in] - "tightness" of the inclusion test
- Returns
- 1 if the point is in the closure of the specified reference cell and 0 otherwise.
Definition at line 2432 of file Intrepid_CellToolsDef.hpp.
|
static |
Checks if a set of points belongs to a reference cell.
Requires cell topology with a reference cell. See Intrepid::CellTools::checkPointwiseInclusion
for admissible ranks and dimensions of the input point array.
- Parameters
-
points [in] - rank-1, 2 or 3 array (point, vector of points, matrix of points) cellTopo [in] - cell topology of the cells stored in cellWorksetthreshold [in] - "tightness" of the inclusion test
- Returns
- 1 if all points are in the closure of the specified reference cell 0 if at least one point is outside the closure of the reference cell
Definition at line 2523 of file Intrepid_CellToolsDef.hpp.
References Intrepid::FieldContainer< Scalar, ArrayTypeId >::resize(), and Intrepid::FieldContainer< Scalar, ArrayTypeId >::size().
|
static |
Checks every point in a set for inclusion in a reference cell.
Requires cell topology with a reference cell. Admissible ranks and dimensions of the
input point array and the corresponding rank and dimension of the output array are as follows:
|-------------------|-------------|-------------|-------------|
| rank: (in)/(out) | 1/1 | 2/1 | 3/2 |
|-------------------|-------------|-------------|-------------|
| points (in) | (D) | (I, D) | (I, J, D) |
|-------------------|-------------|-------------|-------------|
| inRefCell (out) | (1) | (I) | (I, J) |
|------------------ |-------------|-------------|-------------| Example: if points is rank-3 array with dimensions (I, J, D), then
![\[ \mbox{inRefCell}(i,j) = \left\{\begin{array}{rl} 1 & \mbox{if $points(i,j,*)\in\hat{\mathcal{C}}$} \\[2ex] 0 & \mbox{if $points(i,j,*)\notin\hat{\mathcal{C}}$} \end{array}\right. \]](form_114.png)
- Parameters
-
inRefCell [out] - rank-1 or 2 array with results from the pointwise inclusion test refPoints [in] - rank-1,2 or 3 array (point, vector of points, matrix of points) cellTopo [in] - cell topology of the cells stored in cellWorksetthreshold [in] - "tightness" of the inclusion test
Definition at line 2564 of file Intrepid_CellToolsDef.hpp.
|
static |
Checks every point in a set or multiple sets for inclusion in physical cells from a cell workset.
There are two use cases:
- Checks every point from a single point set, stored in a rank-2 array (P,D) for inclusion in a specified physical cell
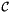 from a cell workset.
from a cell workset. - Checks every point from multiple point sets indexed by a cell ordinal, and stored in a rank-3 (C,P,D) array, for inclusion in the physical cell having the same cell ordinal, for all cells in a cell workset.
For a single point set in a rank-2 array (P,D) and whichCell set to a valid cell ordinal relative to cellWorkset returns a rank-1 (P) array such that
![\[ \mbox{inCell}(p) = \left\{\begin{array}{rl} 1 & \mbox{if $points(p,*)\in {\mathcal{C}}$} \\ [2ex] 0 & \mbox{if $points(p,*)\notin {\mathcal{C}}$} \end{array}\right. \]](form_115.png)
For multiple point sets in a rank-3 array (C,P,D) and whichCell=-1 (default value) returns a rank-2 (C,P) array such that
![\[ \mbox{inCell}(c,p) = \left\{\begin{array}{rl} 1 & \mbox{if $points(c,p,*)\in {\mathcal{C}}$} \\ [2ex] 0 & \mbox{if $points(c,p,*)\notin {\mathcal{C}}$} \end{array}\right. \]](form_116.png)
- Parameters
-
inCell [out] - rank-1 array with results from the pointwise inclusion test points [in] - rank-2 array with dimensions (P,D) with the physical points cellWorkset [in] - rank-3 array with dimensions (C,N,D) with the nodes of the cell workset cellTopo [in] - cell topology of the cells stored in cellWorksetwhichCell [in] - ordinal of the cell used in the inclusion test threshold [in] - tolerance for inclusion tests on the input points
Definition at line 2662 of file Intrepid_CellToolsDef.hpp.
References Intrepid::FieldContainer< Scalar, ArrayTypeId >::resize().
|
static |
Compute cell barycenters.
- Parameters
-
barycenter [out] - array containing cell baycenters cellCoords [in] - array containing cell coordinates
Definition at line 3443 of file Intrepid_CellToolsDef.hpp.
|
static |
Computes non-normalized tangent vectors to physical edges in an edge workset 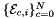 ; (see Subcell worksets for definition of edge worksets).
; (see Subcell worksets for definition of edge worksets).
For every edge in the workset the tangents are computed at the points
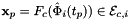 that are images of points from R=[-1,1] on edge
that are images of points from R=[-1,1] on edge 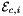 . Returns rank-3 array with dimensions (C,P,D1), D1=2 or D1=3 such that
. Returns rank-3 array with dimensions (C,P,D1), D1=2 or D1=3 such that
![\[ {edgeTangents}(c,p,d) = DF_c(\hat{\Phi}_i(t_p))\cdot {\partial{\hat{\Phi}}_{i}(t_p)\over\partial t}\,; \qquad t_p \in R \]](form_84.png)
In this formula:
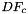 is Jacobian of parent cell
is Jacobian of parent cell 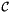 that owns physical edge
that owns physical edge 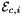 ;
; 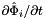 is the (constant) tangent to reference edge
is the (constant) tangent to reference edge 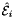 ; see CellTools<Scalar>::getReferenceEdgeTangent that has the same local ordinal as the edges in the workset;
; see CellTools<Scalar>::getReferenceEdgeTangent that has the same local ordinal as the edges in the workset; 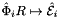 is parametrization of reference edge
is parametrization of reference edge 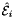 ;
;
- Warning
worksetJacobiansmust contain the values of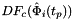 , where
, where ![$ t_p \in R=[-1,1] $](form_90.png) , i.e., Jacobians of the parent cells evaluated at points that are located on reference edge
, i.e., Jacobians of the parent cells evaluated at points that are located on reference edge 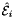 having the same local ordinal as the edges in the workset.
having the same local ordinal as the edges in the workset.
- Parameters
-
edgeTangents [out] - rank-3 array (C,P,D1) with tangents on workset edges worksetJacobians [in] - rank-4 array (C,P,D1,D1) with Jacobians evaluated at ref. edge points worksetEdgeOrd [in] - edge ordinal, relative to ref. cell, of the edge workset parentCell [in] - cell topology of the parent reference cell
Definition at line 2239 of file Intrepid_CellToolsDef.hpp.
Referenced by Intrepid::FunctionSpaceTools::computeEdgeMeasure().
|
static |
Computes non-normalized normal vectors to physical faces in a face workset 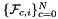 ; (see Subcell worksets for definition of face worksets).
; (see Subcell worksets for definition of face worksets).
For every face in the workset the normals are computed at the points
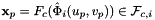 that are images of points from the parametrization domain R on face
that are images of points from the parametrization domain R on face 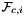 . Returns rank-3 array with dimensions (C,P,D), D=3, such that
. Returns rank-3 array with dimensions (C,P,D), D=3, such that
![\[ {faceNormals}(c,p,d) = \left( DF_c(\hat{\Phi}_i(u_p, v_p))\cdot {\partial\hat{\Phi}_i\over\partial u}\right) \times \left( DF_c(\hat{\Phi}_i(u_p, v_p))\cdot {\partial\hat{\Phi}_i\over\partial v}\right) \,; \qquad (u_p, v_p) \in R \,. \]](form_113.png)
In this formula:
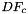 is Jacobian of parent cell
is Jacobian of parent cell 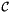 that owns physical face
that owns physical face 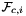 ;
; 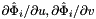 are the (constant) tangents on reference face
are the (constant) tangents on reference face 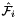 ; see CellTools<Scalar>::getReferenceFaceTangents; that has the same local ordinal as the faces in the workset;
; see CellTools<Scalar>::getReferenceFaceTangents; that has the same local ordinal as the faces in the workset; 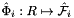 is parametrization of reference face
is parametrization of reference face 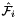 ;
; - R is the parametrization domain for reference face
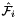 :
: ![\[ R = \left\{\begin{array}{rl} \{(0,0),(1,0),(0,1)\} & \mbox{if $\hat{\mathcal F}_i$ is Triangle} \\[1ex] [-1,1]\times [-1,1] & \mbox{if $\hat{\mathcal F}_i$ is Quadrilateral} \end{array}\right. \]](form_98.png)
- Warning
worksetJacobiansmust contain the values of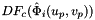 , where
, where 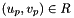 , i.e., Jacobians of the parent cells evaluated at points that are located on reference face
, i.e., Jacobians of the parent cells evaluated at points that are located on reference face 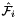 having the same local ordinal as the faces in the workset.
having the same local ordinal as the faces in the workset.
- Parameters
-
faceNormals [out] - rank-3 array (C,P,D), normals at workset faces worksetJacobians [in] - rank-4 array (C,P,D,D) with Jacobians at ref. face points worksetFaceOrd [in] - face ordinal, relative to ref. cell, of the face workset parentCell [in] - cell topology of the parent reference cell
Definition at line 2388 of file Intrepid_CellToolsDef.hpp.
References Intrepid::RealSpaceTools< Scalar >::vecprod().
Referenced by Intrepid::FunctionSpaceTools::computeFaceMeasure().
|
static |
Computes non-normalized tangent vector pairs to physical faces in a face workset 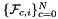 ; (see Subcell worksets for definition of face worksets).
; (see Subcell worksets for definition of face worksets).
For every face in the workset the tangents are computed at the points
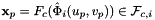 that are images of points from the parametrization domain R on face
that are images of points from the parametrization domain R on face 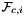 . Returns 2 rank-3 arrays with dimensions (C,P,D), D=3 such that
. Returns 2 rank-3 arrays with dimensions (C,P,D), D=3 such that
![\[ {faceTanU}(c,p,d) = DF_c(\hat{\Phi}_i(u_p, v_p))\cdot {\partial\hat{\Phi}_i\over\partial u};\qquad {faceTanV}(c,p,d) = DF_c(\hat{\Phi}_i(u_p, v_p))\cdot {\partial\hat{\Phi}_{i}\over\partial v}\,; \qquad (u_p, v_p) \in R \,. \]](form_94.png)
In this formula:
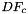 is Jacobian of parent cell
is Jacobian of parent cell 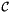 that owns physical face
that owns physical face 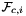 ;
; 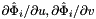 are the (constant) tangents on reference face
are the (constant) tangents on reference face 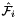 ; see CellTools<Scalar>::getReferenceFaceTangents; that has the same local ordinal as the faces in the workset;
; see CellTools<Scalar>::getReferenceFaceTangents; that has the same local ordinal as the faces in the workset; 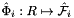 is parametrization of reference face
is parametrization of reference face 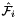 ;
; - R is the parametrization domain for reference face
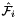 :
: ![\[ R = \left\{\begin{array}{rl} \{(0,0),(1,0),(0,1)\} & \mbox{if $\hat{\mathcal F}_i$ is Triangle} \\[1ex] [-1,1]\times [-1,1] & \mbox{if $\hat{\mathcal F}_i$ is Quadrilateral} \end{array}\right. \]](form_98.png)
- Warning
worksetJacobiansmust contain the values of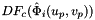 , where
, where 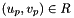 , i.e., Jacobians of the parent cells evaluated at points that are located on reference face
, i.e., Jacobians of the parent cells evaluated at points that are located on reference face 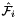 having the same local ordinal as the faces in the workset.
having the same local ordinal as the faces in the workset.
- Parameters
-
faceTanU [out] - rank-3 array (C,P,D), image of ref. face u-tangent at workset faces faceTanV [out] - rank-3 array (C,P,D), image of ref. face u-tangent at workset faces worksetJacobians [in] - rank-4 array (C,P,D,D) with Jacobians at ref. face points worksetFaceOrd [in] - face ordinal, relative to ref. cell, of the face workset parentCell [in] - cell topology of the parent reference cell
Definition at line 2286 of file Intrepid_CellToolsDef.hpp.
|
static |
Computes non-normalized normal vectors to physical sides in a side workset 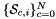 .
.
For every side in the workset the normals are computed at the points
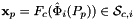 that are images of points from the parametrization domain R on side
that are images of points from the parametrization domain R on side 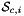 . A side is defined as a subcell of dimension one less than that of its parent cell. Therefore, sides of 2D cells are 1-subcells (edges) and sides of 3D cells are 2-subcells (faces).
. A side is defined as a subcell of dimension one less than that of its parent cell. Therefore, sides of 2D cells are 1-subcells (edges) and sides of 3D cells are 2-subcells (faces).
Returns rank-3 array with dimensions (C,P,D), D = 2 or 3, such that
![\[ {sideNormals}(c,p,d) = \left\{\begin{array}{crl} \displaystyle \left(DF_c(\hat{\Phi}_i(t_p))\cdot {\partial{\hat{\Phi}}_{i}(t_p)\over\partial t}\right)^{\perp} & t_p\in R & \mbox{for 2D parent cells} \\[2ex] \displaystyle \left( DF_c(\hat{\Phi}_i(u_p, v_p))\cdot {\partial\hat{\Phi}_i\over\partial u}\right) \times \left( DF_c(\hat{\Phi}_i(u_p, v_p))\cdot {\partial\hat{\Phi}_i\over\partial v}\right) \,; & (u_p, v_p) \in R & \mbox{for 3D parent cells} \end{array}\right. \]](form_104.png)
In this formula:
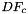 is Jacobian of parent cell
is Jacobian of parent cell 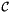 that owns physical side
that owns physical side 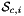 ;
; - For 2D cells:
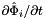 is the (constant) tangent to reference side (edge)
is the (constant) tangent to reference side (edge) 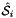 ; see CellTools<Scalar>::getReferenceEdgeTangent, that has the same local ordinal as the sides in the workset;
; see CellTools<Scalar>::getReferenceEdgeTangent, that has the same local ordinal as the sides in the workset; - For 3D cells:
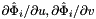 are the (constant) tangents on reference side (face)
are the (constant) tangents on reference side (face) 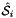 ; see CellTools<Scalar>::getReferenceFaceTangents, that has the same local ordinal as the sides in the workset;
; see CellTools<Scalar>::getReferenceFaceTangents, that has the same local ordinal as the sides in the workset; 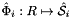 is parametrization of reference side
is parametrization of reference side 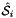 ;
; - R is the parametrization domain for reference side
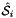 . For 2D parent cells R=[-1,1] and for 3D parent cells
. For 2D parent cells R=[-1,1] and for 3D parent cells ![\[ R = \left\{\begin{array}{rl} \{(0,0),(1,0),(0,1)\} & \mbox{if $\hat{\mathcal S}_i$ is Triangle} \\[1ex] [-1,1]\times [-1,1] & \mbox{if $\hat{\mathcal S}_i$ is Quadrilateral} \end{array}\right. \]](form_107.png)
- Remarks
- For 3D cells the physical side normals coincides with the face normals computed by CellTools<Scalar>::getPhysicalFaceNormals and these two methods are completely equivalent.
- For 2D cells the physical side normals are defined by
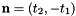 where
where 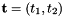 are the physical edge tangents computed by CellTools<Scalar>::getPhysicalEdgeTangents. Therefore, the pairs
are the physical edge tangents computed by CellTools<Scalar>::getPhysicalEdgeTangents. Therefore, the pairs 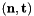 are positively oriented.
are positively oriented.
- Warning
worksetJacobiansmust contain the values of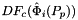 , where
, where 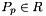 , i.e., Jacobians of the parent cells evaluated at points that are located on reference side
, i.e., Jacobians of the parent cells evaluated at points that are located on reference side 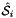 having the same local ordinal as the sides in the workset.
having the same local ordinal as the sides in the workset.
- Parameters
-
sideNormals [out] - rank-3 array (C,P,D), normals at workset sides worksetJacobians [in] - rank-4 array (C,P,D,D) with Jacobians at ref. side points worksetSideOrd [in] - side ordinal, relative to ref. cell, of the side workset parentCell [in] - cell topology of the parent reference cell
Definition at line 2349 of file Intrepid_CellToolsDef.hpp.
Referenced by Intrepid::CubatureControlVolumeSide< Scalar, ArrayPoint, ArrayWeight >::getCubature().
|
static |
Computes constant tangent vectors to edges of 2D or 3D reference cells.
Returns rank-1 array with dimension (D), D=2 or D=3; such that
![\[ {refEdgeTangent}(*) = \hat{\bf t}_i = {\partial\hat{\Phi}_i(t)\over\partial t}\,, \]](form_54.png)
where ![$\hat{\Phi}_i : R =[-1,1]\mapsto \hat{\mathcal E}_i$](form_55.png) is the parametrization map of the specified reference edge
is the parametrization map of the specified reference edge 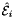 , given by
, given by
![\[ \hat{\Phi}_i(t) = \left\{\begin{array}{ll} (\hat{x}(t),\hat{y}(t),\hat{z}(t)) & \mbox{for 3D parent cells} \\[1ex] (\hat{x}(t),\hat{y}(t)) & \mbox{for 2D parent cells} \\[1ex] \end{array}\right. \]](form_57.png)
The length of computed edge tangents is one-half the length of their associated edges:
![\[ |\hat{\bf t}_i | = {1\over 2} |\hat{\mathcal E}_i |\,. \]](form_58.png)
Because the edges of all reference cells are always affine images of [-1,1], the edge tangent is constant vector field.
- Parameters
-
refEdgeTangent [out] - rank-1 array (D) with the edge tangent; D = cell dimension edgeOrd [in] - ordinal of the edge whose tangent is computed parentCell [in] - cell topology of the parent reference cell
Definition at line 2094 of file Intrepid_CellToolsDef.hpp.
Referenced by Intrepid::Basis_HCURL_TET_In_FEM< Scalar, ArrayScalar >::Basis_HCURL_TET_In_FEM(), and Intrepid::Basis_HCURL_TRI_In_FEM< Scalar, ArrayScalar >::Basis_HCURL_TRI_In_FEM().
|
static |
Computes constant normal vectors to faces of 3D reference cell.
Returns rank-1 array with dimension (D), D=3 such that
![\[ {refFaceNormal}(*) = \hat{\bf n}_i = {\partial\hat{\Phi}_{i}\over\partial u} \times {\partial\hat{\Phi}_{i}\over\partial v} \]](form_77.png)
where 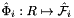 is the parametrization map of the specified reference face
is the parametrization map of the specified reference face 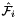 given by
given by
![\[ \hat{\Phi}_i(u,v) =(\hat{x}(u,v),\hat{y}(u,v),\hat{z}(u,v)) \]](form_63.png)
and
![\[ R = \left\{\begin{array}{rl} \{(0,0),(1,0),(0,1)\} & \mbox{if ${\mathcal F}$ is Triangle} \\[1ex] [-1,1]\times [-1,1] & \mbox{if ${\mathcal F}$ is Quadrilateral} \,. \end{array}\right. \]](form_78.png)
The length of computed face normals is proportional to face area:
![\[ |\hat{\bf n}_i | = \left\{\begin{array}{rl} 2 \mbox{Area}(\hat{\mathcal F}_i) & \mbox{if $\hat{\mathcal F}_i$ is Triangle} \\[1ex] \mbox{Area}(\hat{\mathcal F}_i) & \mbox{if $\hat{\mathcal F}_i$ is Quadrilateral} \,. \end{array}\right. \]](form_72.png)
Because the faces of all reference cells are always affine images of R , the coordinate functions 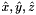 of the parametrization map are linear and the face normal is a constant vector.
of the parametrization map are linear and the face normal is a constant vector.
- Remarks
- The method CellTools::getReferenceFaceTangents computes the reference face tangents
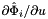 and
and 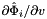 .
.
- Parameters
-
refFaceNormal [out] - rank-1 array (D) with (constant) face normal faceOrd [in] - ordinal of the face whose normal is computed parentCell [in] - cell topology of the parent reference cell
Definition at line 2209 of file Intrepid_CellToolsDef.hpp.
References Intrepid::RealSpaceTools< Scalar >::vecprod().
|
static |
Computes pairs of constant tangent vectors to faces of a 3D reference cells.
Returns 2 rank-1 arrays with dimension (D), D=3, such that
![\[ {refFaceTanU}(*) = \hat{\bf t}_{i,u} = {\partial\hat{\Phi}_i(u,v)\over\partial u} = \left({\partial\hat{x}(u,v)\over\partial u}, {\partial\hat{y}(u,v)\over\partial u}, {\partial\hat{z}(u,v)\over\partial u} \right) ; \]](form_59.png)
![\[ {refFaceTanV}(*) = \hat{\bf t}_{i,v} = {\partial\hat{\Phi}_i(u,v)\over \partial v} = \left({\partial\hat{x}(u,v)\over\partial v}, {\partial\hat{y}(u,v)\over\partial v}, {\partial\hat{z}(u,v)\over\partial v} \right)\,; \]](form_60.png)
where 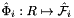 is the parametrization map of the specified reference face
is the parametrization map of the specified reference face 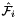 given by
given by
![\[ \hat{\Phi}_i(u,v) =(\hat{x}(u,v),\hat{y}(u,v),\hat{z}(u,v)) \]](form_63.png)
and
![\[ R = \left\{\begin{array}{rl} \{(0,0),(1,0),(0,1)\} & \mbox{if $\hat{\mathcal F}_i$ is Triangle} \\[1ex] [-1,1]\times [-1,1] & \mbox{if $\hat{\mathcal F}_i$ is Quadrilateral} \,. \end{array}\right. \]](form_64.png)
Because the faces of all reference cells are always affine images of R , the coordinate functions 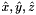 of the parametrization map are linear and the face tangents are constant vectors.
of the parametrization map are linear and the face tangents are constant vectors.
- Parameters
-
refFaceTanU [out] - rank-1 array (D) with (constant) tangent in u-direction refFaceTanV [out] - rank-1 array (D) with (constant) tangent in v-direction faceOrd [in] - ordinal of the face whose tangents are computed parentCell [in] - cell topology of the parent 3D reference cell
Definition at line 2130 of file Intrepid_CellToolsDef.hpp.
Referenced by Intrepid::Basis_HCURL_TET_In_FEM< Scalar, ArrayScalar >::Basis_HCURL_TET_In_FEM().
|
static |
Retrieves the Cartesian coordinates of a reference cell node.
Returns Cartesian coordinates of a reference cell node. Requires cell topology
with a reference cell. Node coordinates are always returned as an (x,y,z)-triple
regardlesss of the actual topological cell dimension. The unused coordinates are
set to zero, e.g., node 0 of Line<2> is returned as {-1,0,0}.
- Remarks
- Because the nodes of a cell with a base topology coincide with its vertices, for cells with base topology this method is equivalent to CellTools<Scalar>::getReferenceVertex.
- Parameters
-
cell [in] - cell topology of the cell vertexOrd [in] - node ordinal
- Returns
- pointer to array with the (x,y,z) coordinates of the specified reference vertex
Definition at line 529 of file Intrepid_CellToolsDef.hpp.
Referenced by Intrepid::CellTools< Scalar >::getReferenceSubcellNodes().
|
static |
Computes constant normal vectors to sides of 2D or 3D reference cells.
A side is defined as a subcell of dimension one less than that of its parent cell.
Therefore, sides of 2D cells are 1-subcells (edges) and sides of 3D cells
are 2-subcells (faces).
Returns rank-1 array with dimension (D), D = 2 or 3 such that
![\[ {refSideNormal}(*) = \hat{\bf n}_i = \left\{\begin{array}{rl} \displaystyle \left({\partial\hat{\Phi}_i(t)\over\partial t}\right)^{\perp} & \mbox{for 2D parent cells} \\[2ex] \displaystyle {\partial\hat{\Phi}_{i}\over\partial u} \times {\partial\hat{\Phi}_{i}\over\partial v} & \mbox{for 3D parent cells} \end{array}\right. \]](form_66.png)
where 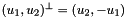 , and
, and 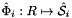 is the parametrization map of the specified reference side
is the parametrization map of the specified reference side 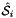 given by
given by
![\[ \hat{\Phi}_i(u,v) = \left\{\begin{array}{rl} (\hat{x}(t),\hat{y}(t)) & \mbox{for 2D parent cells} \\[1ex] (\hat{x}(u,v),\hat{y}(u,v),\hat{z}(u,v)) & \mbox{for 3D parent cells} \end{array}\right. \]](form_70.png)
For sides of 2D cells R=[-1,1] and for sides of 3D cells
![\[ R = \left\{\begin{array}{rl} \{(0,0),(1,0),(0,1)\} & \mbox{if $\hat{\mathcal S}_i$ is Triangle} \\[1ex] [-1,1]\times [-1,1] & \mbox{if $\hat{\mathcal S}_i$ is Quadrilateral} \,. \end{array}\right. \]](form_71.png)
For 3D cells the length of computed side normals is proportional to side area:
![\[ |\hat{\bf n}_i | = \left\{\begin{array}{rl} 2 \mbox{Area}(\hat{\mathcal F}_i) & \mbox{if $\hat{\mathcal F}_i$ is Triangle} \\[1ex] \mbox{Area}(\hat{\mathcal F}_i) & \mbox{if $\hat{\mathcal F}_i$ is Quadrilateral} \,. \end{array}\right. \]](form_72.png)
For 2D cells the length of computed side normals is proportional to side length:
![\[ |\hat{\bf n}_i | = {1\over 2} |\hat{\mathcal F}_i |\,. \]](form_73.png)
Because the sides of all reference cells are always affine images of R , the coordinate functions 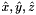 of the parametrization maps are linear and the side normal is a constant vector.
of the parametrization maps are linear and the side normal is a constant vector.
- Remarks
- For 3D cells the reference side normal coincides with the face normal computed by CellTools<Scalar>::getReferenceFaceNormal and these two methods are completely equivalent.
- For 2D cells the reference side normal is defined by
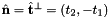 where
where 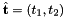 is the tangent vector computed by CellTools<Scalar>::getReferenceEdgeTangent. Therefore, the pair
is the tangent vector computed by CellTools<Scalar>::getReferenceEdgeTangent. Therefore, the pair 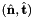 is positively oriented.
is positively oriented.
- Parameters
-
refSideNormal [out] - rank-1 array (D) with (constant) side normal sideOrd [in] - ordinal of the side whose normal is computed parentCell [in] - cell topology of the parent reference cell
Definition at line 2175 of file Intrepid_CellToolsDef.hpp.
|
static |
Retrieves the Cartesian coordinates of all nodes of a reference subcell.
Returns rank-2 array with the Cartesian coordinates of the nodes of the
specified reference cell subcell. Requires cell topology with a reference cell.
- Parameters
-
subcellNodes [out] - rank-2 (N,D) array with the Cartesian coordinates of the reference subcell nodes subcellDim [in] - dimension of the subcell; 0 <= subcellDim <= parentCell dimension subcellOrd [in] - ordinal of the subcell parentCell [in] - topology of the cell that owns the subcell
- Remarks
- When
subcellDim= dimension of theparentCellthis method returns the Cartesian coordinates of the nodes of the reference cell itself. Note that this requiressubcellOrd=0.
Definition at line 788 of file Intrepid_CellToolsDef.hpp.
References Intrepid::CellTools< Scalar >::getReferenceNode().
|
static |
Retrieves the Cartesian coordinates of all vertices of a reference subcell.
Returns rank-2 array with the Cartesian coordinates of the vertices of the
specified reference cell subcell. Requires cell topology with a reference cell.
- Parameters
-
subcellVertices [out] - rank-2 (V,D) array with the Cartesian coordinates of the reference subcell vertices subcellDim [in] - dimension of the subcell; 0 <= subcellDim <= parentCell dimension subcellOrd [in] - ordinal of the subcell parentCell [in] - topology of the cell that owns the subcell
- Remarks
- When
subcellDim= dimension of theparentCellthis method returns the Cartesian coordinates of the vertices of the reference cell itself. Note that this requires subcellOrd=0.
Definition at line 490 of file Intrepid_CellToolsDef.hpp.
|
static |
Retrieves the Cartesian coordinates of a reference cell vertex.
Requires cell topology with a reference cell. Vertex coordinates are always returned
as an (x,y,z)-triple regardlesss of the actual topological cell dimension. The unused
coordinates are set to zero, e.g., vertex 0 of Line<2> is returned as {-1,0,0}.
- Parameters
-
cell [in] - cell topology of the cell vertexOrd [in] - vertex ordinal
- Returns
- pointer to array with the (x,y,z) coordinates of the specified reference vertex
Definition at line 471 of file Intrepid_CellToolsDef.hpp.
|
staticprivate |
Returns array with the coefficients of the parametrization maps for the edges or faces of a reference cell topology.
See CellTools<Scalar>::setSubcellParametrization and Section \ref sec_cell_topology_subcell_map
more information about parametrization maps.
- Parameters
-
subcellDim [in] - dimension of subcells whose parametrization map is returned parentCell [in] - topology of the reference cell owning the subcells
- Returns
- FieldContainer<double> with the coefficients of the parametrization map for all subcells of the specified dimension.
Definition at line 60 of file Intrepid_CellToolsDef.hpp.
|
static |
Computes coordinates of sub-control volumes in each primary cell.
To build the system of equations for the control volume finite element method we need to compute geometric data for integration over control volumes. A control volume is polygon or polyhedron that surrounds a primary cell node and has vertices that include the surrounding primary cells' barycenter, edge midpoints, and face midpoints if in 3-d.
When using element-based assembly of the discrete equations over the primary mesh, a single element will contain a piece of each control volume surrounding each of the primary cell nodes. This piece of control volume (sub-control volume) is always a quadrilateral in 2-d and a hexahedron in 3-d.
In 2-d the sub-control volumes are defined in the following way:
Quadrilateral primary element:
O________M________O
| | |
| 3 | 2 | B = cell barycenter
| | | O = primary cell nodes
M________B________M M = cell edge midpoints
| | |
| 0 | 1 | sub-control volumes 0, 1, 2, 3
| | |
O________M________O
Triangle primary element:
O
/ \
/ \ B = cell barycenter
/ \ O = primary cell nodes
M 2 M M = cell edge midpoints
/ \ / \
/ \ B / \ sub-control volumes 0, 1, 2
/ | \
/ 0 | 1 \
O________M________OIn 3-d the sub-control volumes are defined by the primary cell face centers and edge midpoints. The eight sub-control volumes for a hexahedron are shown below:
O__________E__________O
/| /| /|
E_|________F_|________E |
/| | /| | /| |
O_|_|______E_|_|______O | | O = primary cell nodes
| | E------|-|-F------|-|-E B = cell barycenter
| |/| | |/| | |/| F = cell face centers
| F-|------|-B-|------|-F | E = cell edge midpoints
|/| | |/| | |/| |
E_|_|______F_|_|______E | |
| | O------|-|-E------|-|-O
| |/ | |/ | |/
| E--------|-F--------|-E
|/ |/ |/
O__________E__________O- Parameters
-
subCVCoords [out] - array containing sub-control volume coordinates cellCoords [in] - array containing coordinates of primary cells primaryCell [in] - primary cell topology
Definition at line 3223 of file Intrepid_CellToolsDef.hpp.
Referenced by Intrepid::CubatureControlVolumeSide< Scalar, ArrayPoint, ArrayWeight >::getCubature(), Intrepid::CubatureControlVolume< Scalar, ArrayPoint, ArrayWeight >::getCubature(), and Intrepid::CubatureControlVolumeBoundary< Scalar, ArrayPoint, ArrayWeight >::getCubature().
|
static |
Checks if a cell topology has reference cell.
- Parameters
-
cell [in] - cell topology
- Returns
- 1 if the cell topology has reference cell, 0 oterwise
Definition at line 839 of file Intrepid_CellToolsDef.hpp.
|
static |
Computes F, the reference-to-physical frame map.
There are 3 use cases:
- Applies
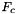 for a specified physical cell
for a specified physical cell 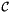 from a cell workset to a single point set stored in a rank-2 (P,D) array;
from a cell workset to a single point set stored in a rank-2 (P,D) array; - Applies
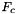 for all cells in a cell workset to a single point set stored in a rank-2 (P,D) array;
for all cells in a cell workset to a single point set stored in a rank-2 (P,D) array; - Applies
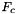 for all cells in a cell workset to multiple point sets having the same number of points, indexed by cell ordinal, and stored in a rank-3 (C,P,D) array;
for all cells in a cell workset to multiple point sets having the same number of points, indexed by cell ordinal, and stored in a rank-3 (C,P,D) array;
For a single point set in a rank-2 array (P,D) and whichCell set to a valid cell ordinal relative to cellWorkset returns a rank-2 (P,D) array such that
![\[ \mbox{physPoints}(p,d) = \Big(F_c(\mbox{refPoint}(p,*)) \Big)_d \quad \mbox{for $0\le c < C$ - fixed} \]](form_43.png)
For a single point set in a rank-2 array (P,D) and whichCell=-1 (default value) returns a rank-3 (C,P,D) array such that
![\[ \mbox{physPoints}(c,p,d) = \Big(F_c(\mbox{refPoint}(p,*)) \Big)_d \quad c=0,\ldots, C \]](form_44.png)
For multiple point sets in a rank-3 (C,P,D) array returns a rank-3 (C,P,D) array such that
![\[ \mbox{physPoints}(c,p,d) = \Big(F_c(\mbox{refPoint}(c,p,*)) \Big)_d \quad c=0,\ldots, C \]](form_45.png)
This corresponds to mapping multiple sets of reference points to a matching number of physical cells and requires the default value whichCell=-1.
Requires cell topology with a reference cell. See Section Reference-to-physical cell mapping for definition of the mapping function. Presently supported cell topologies are
- 1D:
Line<2> - 2D:
Triangle<3>,Triangle<6>,Quadrilateral<4>,Quadrilateral<9> - 3D:
Tetrahedron<4>,Tetrahedron<10>,Hexahedron<8>,Hexahedron<27>The default \c whichCell = -1 requires rank-3 output array and forces application of all reference-to-physical frame mappings corresponding to the cells stored in \c cellWorkset. Application of a single mapping is forced by selecting a valid cell ordinal \c whichCell and requires rank-2 input/output point arrays.
- Warning
- The array
refPointsrepresents an arbitrary set of points in the reference frame that are not required to be in the reference cell corresponding to the specified cell topology. As a result, the images of these points under a given reference-to-physical map are not necessarily contained in the physical cell that is the image of the reference cell under that map. CellTools provides several inclusion tests methods to check whether or not the points are inside a reference cell.
- Parameters
-
physPoints [out] - rank-3/2 array with dimensions (C,P,D)/(P,D) with the images of the ref. points refPoints [in] - rank-3/2 array with dimensions (C,P,D)/(P,D) with points in reference frame cellWorkset [in] - rank-3 array with dimensions (C,N,D) with the nodes of the cell workset cellTopo [in] - cell topology of the cells stored in cellWorksetwhichCell [in] - ordinal of the cell that defines the reference-to-physical map; default is -1
- Todo:
- Implement method for non-standard (shell, beam, etc) topologies.
Definition at line 1447 of file Intrepid_CellToolsDef.hpp.
Referenced by Intrepid::CubaturePolygon< Scalar, ArrayPoint, ArrayWeight >::CubaturePolygon().
|
static |
Computes 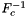 , the inverse of the reference-to-physical frame map using a default initial guess.
, the inverse of the reference-to-physical frame map using a default initial guess.
There are two use cases:
- Applies
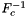 for a specified physical cell
for a specified physical cell 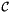 from a cell workset to a single set of points stored in a rank-2 (P,D) array;
from a cell workset to a single set of points stored in a rank-2 (P,D) array; - Applies
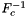 for all cells in a cell workset to multiple point sets having the same number of points, indexed by cell ordinal, and stored in a rank-3 (C,P,D) array (default mode).
for all cells in a cell workset to multiple point sets having the same number of points, indexed by cell ordinal, and stored in a rank-3 (C,P,D) array (default mode).
For a single point set in a rank-2 array (P,D) returns a rank-2 (P,D) array such that
![\[ \mbox{refPoints}(p,d) = \Big(F^{-1}_c(physPoint(p,*)) \Big)_d \]](form_47.png)
The whichCell argument selects the physical cell and is required to be a valid cell ordinal for cellWorkset array.
For multiple point sets in a rank-3 (C,P,D) array returns a rank-3 (C,P,D) array such that
![\[ \mbox{refPoints}(c,p,d) = \Big(F^{-1}_c(physPoint(c,p,*)) \Big)_d \]](form_48.png)
The default value whichCell=-1 selects this mode.
Requires cell topology with a reference cell. See Section Reference-to-physical cell mapping for definition of the mapping function. Presently supported cell topologies are
- 1D:
Line<2> - 2D:
Triangle<3>,Triangle<6>,Quadrilateral<4>,Quadrilateral<9> - 3D:
Tetrahedron<4>,Tetrahedron<10>,Hexahedron<8>,Hexahedron<27>
- Warning
- Computation of the inverse map in this method uses default selection of the initial guess based on cell topology:
Linetopologies: line center (0)Triangletopologies: the point (1/3, 1/3)Quadrilateraltopologies: the point (0, 0)Tetrahedrontopologies: the point (1/6, 1/6, 1/6)Hexahedrontopologies: the point (0, 0, 0)Wedgetopologies: the point (1/2, 1/2, 0) For some cells with extended topologies, these initial guesses may not be good enough for Newton's method to converge in the allotted number of iterations. A version of this method with user-supplied initial guesses is also available.
-
The array
physPointsrepresents an arbitrary set (or sets) of points in the physical frame that are not required to belong in the physical cell (cells) that define(s) the reference to physical mapping. As a result, the images of these points in the reference frame are not necessarily contained in the reference cell corresponding to the specified cell topology.
- Parameters
-
refPoints [out] - rank-3/2 array with dimensions (C,P,D)/(P,D) with the images of the physical points physPoints [in] - rank-3/2 array with dimensions (C,P,D)/(P,D) with points in physical frame cellWorkset [in] - rank-3 array with dimensions (C,N,D) with the nodes of the cell workset whichCell [in] - ordinal of the cell that defines the reference-to-physical map; default is -1 cellTopo [in] - cell topology of the cells stored in cellWorkset
- Todo:
- Implement method for non-standard (shell, beam, etc) topologies.
Definition at line 1662 of file Intrepid_CellToolsDef.hpp.
References Intrepid::FieldContainer< Scalar, ArrayTypeId >::resize().
Referenced by Intrepid::PointTools::getWarpBlendLatticeTetrahedron(), and Intrepid::PointTools::getWarpBlendLatticeTriangle().
|
static |
Computation of 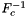 , the inverse of the reference-to-physical frame map using user-supplied initial guess.
, the inverse of the reference-to-physical frame map using user-supplied initial guess.
There are two use cases:
- Applies
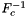 for a specified physical cell
for a specified physical cell 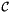 from a cell workset to a single set of points stored in a rank-2 (P,D) array;
from a cell workset to a single set of points stored in a rank-2 (P,D) array; - Applies
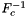 for all cells in a cell workset to multiple point sets having the same number of points, indexed by cell ordinal, and stored in a rank-3 (C,P,D) array (default mode).
for all cells in a cell workset to multiple point sets having the same number of points, indexed by cell ordinal, and stored in a rank-3 (C,P,D) array (default mode).
For a single point set in a rank-2 array (P,D) returns a rank-2 (P,D) array such that
![\[ \mbox{refPoints}(p,d) = \Big(F^{-1}_c(physPoint(p,*)) \Big)_d \]](form_47.png)
The whichCell argument selects the physical cell and is required to be a valid cell ordinal for cellWorkset array.
For multiple point sets in a rank-3 (C,P,D) array returns a rank-3 (C,P,D) array such that
![\[ \mbox{refPoints}(c,p,d) = \Big(F^{-1}_c(physPoint(c,p,*)) \Big)_d \]](form_48.png)
The default value whichCell=-1 selects this mode.
Requires cell topology with a reference cell. See Section Reference-to-physical cell mapping for definition of the mapping function. Presently supported cell topologies are
- 1D:
Line<2> - 2D:
Triangle<3>,Triangle<6>,Quadrilateral<4>,Quadrilateral<9> - 3D:
Tetrahedron<4>,Tetrahedron<10>,Hexahedron<8>,Hexahedron<27>
- Warning
- The array
physPointsrepresents an arbitrary set (or sets) of points in the physical frame that are not required to belong in the physical cell (cells) that define(s) the reference to physical mapping. As a result, the images of these points in the reference frame are not necessarily contained in the reference cell corresponding to the specified cell topology.
- Parameters
-
refPoints [out] - rank-3/2 array with dimensions (C,P,D)/(P,D) with the images of the physical points initGuess [in] - rank-3/2 array with dimensions (C,P,D)/(P,D) with the initial guesses for each point physPoints [in] - rank-3/2 array with dimensions (C,P,D)/(P,D) with points in physical frame cellWorkset [in] - rank-3 array with dimensions (C,N,D) with the nodes of the cell workset whichCell [in] - ordinal of the cell that defines the reference-to-physical map; default is -1 cellTopo [in] - cell topology of the cells stored in cellWorkset
Definition at line 1899 of file Intrepid_CellToolsDef.hpp.
References Intrepid::RealSpaceTools< Scalar >::add(), INTREPID_MAX_NEWTON, Intrepid::RealSpaceTools< Scalar >::matvec(), Intrepid::FieldContainer< Scalar, ArrayTypeId >::resize(), Intrepid::RealSpaceTools< Scalar >::subtract(), and Intrepid::RealSpaceTools< Scalar >::vectorNorm().
|
static |
Computes parameterization maps of 1- and 2-subcells of reference cells.
Applies \form#49, the parametrization map of a subcell \form#27
from a given reference cell, to a set of points in the parametrization domain
\e R of \form#27. Returns a rank-2 array with dimensions
(P,D) where for 1-subcells:
![\[ {subcellPoints}(p,*) = \hat{\Phi}_i(t_p) \quad\mbox{and}\quad \hat{\Phi}_i(t_p) = \left\{ \begin{array}{ll} (\hat{x}(t_p),\hat{y}(t_p),\hat{z}(t_p)) & \mbox{for 3D parent cells}\\[1.5ex] (\hat{x}(t_p),\hat{y}(t_p)) & \mbox{for 2D parent cells} \end{array} \right. \quad t_p \in R = [-1,1] \,; \]](form_50.png)
for 2-subcells:
![\[ {subcellPoints}(p,*) = \hat{\Phi}_i(u_p,v_p)\quad\mbox{and}\quad \hat{\Phi}_i(u_p,v_p) = (\hat{x}(u_p,v_p), \hat{y}(u_p,v_p), \hat{z}(u_p, v_p)) \quad (u_p,v_p)\in R \]](form_51.png)
and
![\[ R = \left\{\begin{array}{rl} \{(0,0),(1,0),(0,1)\} & \mbox{if face is Triangle} \\[1ex] [-1,1]\times [-1,1] & \mbox{if face is Quadrilateral} \end{array}\right. \]](form_52.png)
- Remarks
- Parametrization of 1-subcells is defined for all 2D and 3D cell topologies with reference cells, including special 2D and 3D topologies such as shell and beams.
- Parametrization of 2-subcells is defined for all 3D cell topologies with reference cells, including special 3D topologies such as shells.
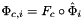 of each subcell in the workset to
of each subcell in the workset to paramPoints. Here c is ordinal of a parent cell, relative to subcell workset, and i is subcell ordinal, relative to a reference cell, of the subcell workset. See Section Subcell worksets for definition of subcell workset and Section Parametrization of physical 1- and 2-subcells for definition of parametrization maps.
- Parameters
-
refSubcellPoints [out] - rank-2 (P,D1) array with images of parameter space points paramPoints [in] - rank-2 (P,D2) array with points in 1D or 2D parameter domain subcellDim [in] - dimension of the subcell where points are mapped to subcellOrd [in] - subcell ordinal parentCell [in] - cell topology of the parent cell.
Definition at line 2027 of file Intrepid_CellToolsDef.hpp.
Referenced by Intrepid::Basis_HCURL_TET_In_FEM< Scalar, ArrayScalar >::Basis_HCURL_TET_In_FEM(), Intrepid::Basis_HCURL_TRI_In_FEM< Scalar, ArrayScalar >::Basis_HCURL_TRI_In_FEM(), Intrepid::Basis_HDIV_TET_In_FEM< Scalar, ArrayScalar >::Basis_HDIV_TET_In_FEM(), Intrepid::Basis_HDIV_TRI_In_FEM< Scalar, ArrayScalar >::Basis_HDIV_TRI_In_FEM(), Intrepid::CubatureControlVolumeSide< Scalar, ArrayPoint, ArrayWeight >::getCubature(), and Intrepid::CubatureControlVolumeBoundary< Scalar, ArrayPoint, ArrayWeight >::getCubature().
|
static |
Prints the reference space coordinates of the vertices of the specified subcell.
- Parameters
-
subcellDim [in] - dimension of the subcell where points are mapped to subcellOrd [in] - subcell ordinal parentCell [in] - cell topology of the parent cell.
Definition at line 3140 of file Intrepid_CellToolsDef.hpp.
|
static |
Prints the nodes of a subcell from a cell workset.
Definition at line 3180 of file Intrepid_CellToolsDef.hpp.
|
static |
Computes the determinant of the Jacobian matrix DF of the reference-to-physical frame map F.
Returns rank-2 or rank-1 array with dimensions (C,P)/(P) such that
![\[ \mbox{jacobianDet}(c,p) = \mbox{det}(\mbox{jacobian}(c,p,*,*)) \quad c=0,\ldots, C \quad\mbox{or}\quad \mbox{jacobianDet}(p) = \mbox{det}(\mbox{jacobian}(p,*,*)) \]](form_41.png)
- Parameters
-
jacobianDet [out] - rank-2/1 array with dimensions (C,P)/(P) with Jacobian determinants jacobian [in] - rank-4/3 array with dimensions (C,P,D,D)/(P,D,D) with the Jacobians
Definition at line 1314 of file Intrepid_CellToolsDef.hpp.
Referenced by Intrepid::CubaturePolygon< Scalar, ArrayPoint, ArrayWeight >::CubaturePolygon(), Intrepid::CubatureControlVolume< Scalar, ArrayPoint, ArrayWeight >::getCubature(), and Intrepid::CubatureControlVolumeBoundary< Scalar, ArrayPoint, ArrayWeight >::getCubature().
|
static |
Computes the inverse of the Jacobian matrix DF of the reference-to-physical frame map F.
Returns rank-4 or rank-3 array with dimensions (C,P,D,D) or (P,D,D) such that
![\[ \mbox{jacobianInv}(c,p,*,*) = \mbox{jacobian}^{-1}(c,p,*,*) \quad c = 0,\ldots, C \quad\mbox{or}\quad \mbox{jacobianInv}(p,*,*) = \mbox{jacobian}^{-1}(p,*,*) \]](form_40.png)
- Parameters
-
jacobianInv [out] - rank-4/3 array with dimensions (C,P,D,D)/(P,D,D) with the inverse Jacobians jacobian [in] - rank-4/3 array with dimensions (C,P,D,D)/(P,D,D) with the Jacobians
Definition at line 1283 of file Intrepid_CellToolsDef.hpp.
References Intrepid::RealSpaceTools< Scalar >::inverse().
|
staticprivate |
Defines orientation-preserving parametrizations of reference edges and faces of cell topologies with reference cells.
Given an edge {V0, V1} of some reference cell, its parametrization is a mapping from
[-1,1] onto the edge. Parametrization of a triangular face {V0,V1,V2} is mapping from
the standard 2-simplex {(0,0,0), (1,0,0), (0,1,0)}, embedded in 3D onto that face.
Parametrization of a quadrilateral face {V0,V1,V2,V3} is mapping from the standard
2-cube {(-1,-1,0),(1,-1,0),(1,1,0),(-1,1,0)}, embedded in 3D, onto that face.
This method computes the coefficients of edge and face parametrization maps and stores
them in static arrays owned by CellTools<Scalar>::getSubcellParametrization method.
All mappings are affine and orientation-preserving, i.e., they preserve the tangent
and normal directions implied by the vertex order of the edge or the face relative to
the reference cell:
- the tangent on [-1,1] from -1 in the direction of 1 is mapped to a tangent on edge {V0,V1} from V0 in the direction of V1 (the forward direction of the edge determined by its start and end vertices)
- the normal in the direction of (0,0,1) to the standard 2-simplex {(0,0,0),(1,0,0),(0,1,0)} and the standard 2-cube {(-1,-1,0),(1,-1,0),(1,1,0),(-1,1,0)} is mapped to a normal on {V0,V1,V2} and {V0,V1,V2,V3}, determined according to the right-hand rule (see http://mathworld.wolfram.com/Right-HandRule.html for definition of right-hand rule and Section Section sec_cell_topology_subcell_map for further details).
Because faces of all reference cells supported in Intrepid are affine images of either the standard 2-simplex or the standard 2-cube, the coordinate functions of the respective parmetrization maps are linear polynomials in the parameter variables (u,v), i.e., they are of the form F_i(u,v)=C_0(i)+C_1(i)u+C_2(i)v; 0<=i<3 (face parametrizations are supported only for 3D cells, thus parametrization maps have 3 coordinate functions). As a result, application of these maps is independent of the face type which is convenient for cells such as Wedge or Pyramid that have both types of faces. Also, coefficients of coordinate functions for all faces can be stored together in the same array.
- Parameters
-
subcellParametrization [out] - array with the coefficients of the parametrization map subcellDim [in] - dimension of the subcells being parametrized (1 or 2) parentCell [in] - topology of the parent cell owning the subcells.
Definition at line 327 of file Intrepid_CellToolsDef.hpp.
References Intrepid::FieldContainer< Scalar, ArrayTypeId >::resize().
|
staticprivate |
Validates arguments to Intrepid::CellTools::checkPointwiseInclusion.
- Parameters
-
inCell [out] - rank-1 (P) array required physPoints [in] - rank-2 (P,D) array required cellWorkset [in] - rank-3 (C,N,D) array required whichCell [in] - 0 <= whichCell < C required cellTopo [in] - cell topology with a reference cell required
Definition at line 3055 of file Intrepid_CellToolsDef.hpp.
|
staticprivate |
Validates arguments to Intrepid::CellTools::mapToPhysicalFrame.
- Parameters
-
physPoints [in] - rank-3 (C,P,D) array or rank-2 (P,D) array required refPoints [in] - rank-3 (C,P,D) array or rank-2 (P,D) array required cellWorkset [in] - rank-3 (C,N,D) array required whichCell [in] - default = -1 or 0 <= whichCell < C required cellTopo [in] - cell topology with a reference cell required
Definition at line 2900 of file Intrepid_CellToolsDef.hpp.
|
staticprivate |
Validates arguments to Intrepid::CellTools::mapToReferenceFrame with default initial guess.
- Parameters
-
physPoints [in] - rank-3 (C,P,D) array or rank-2 (P,D) array required refPoints [in] - rank-3 (C,P,D) array or rank-2 (P,D) array required cellWorkset [in] - rank-3 (C,N,D) array required whichCell [in] - default = -1 or 0 <= whichCell < C required cellTopo [in] - cell topology with a reference cell required
Definition at line 2991 of file Intrepid_CellToolsDef.hpp.
|
staticprivate |
Validates arguments to Intrepid::CellTools::mapToReferenceFrame with user-defined initial guess.
- Parameters
-
physPoints [in] - rank-3 (C,P,D) array or rank-2 (P,D) array required initGuess [in] - rank and dimensions must match those of physPoints refPoints [in] - rank-3 (C,P,D) array or rank-2 (P,D) array required cellWorkset [in] - rank-3 (C,N,D) array required whichCell [in] - default = -1 or 0 <= whichCell < C required cellTopo [in] - cell topology with a reference cell required
Definition at line 3037 of file Intrepid_CellToolsDef.hpp.
|
staticprivate |
Validates arguments to Intrepid::CellTools::setJacobian.
- Parameters
-
jacobian [in] - rank-4 (C,P,D,D) array or rank-3 (P,D,D) array required points [in] - rank-2 (P,D) or rank-3 (C,P,D) array required cellWorkset [in] - rank-3 (C,N,D) array required whichCell [in] - default = -1 or 0 <= whichCell < C required cellTopo [in] - cell topology with a reference cell required
Definition at line 2715 of file Intrepid_CellToolsDef.hpp.
|
staticprivate |
Validates arguments to Intrepid::CellTools::setJacobianDet.
- Parameters
-
jacobianDet [in] - rank = (jacobian rank - 2) required jacobian [in] - rank-4 (C,P,D,D) array or rank-3 (P,D,D) array required
Definition at line 2857 of file Intrepid_CellToolsDef.hpp.
|
staticprivate |
Validates arguments to Intrepid::CellTools::setJacobianInv.
- Parameters
-
jacobianInv [in] - rank and dimensions must match jacobian array jacobian [in] - rank-4 (C,P,D,D) array or rank-3 (P,D,D) array required
Definition at line 2829 of file Intrepid_CellToolsDef.hpp.
The documentation for this class was generated from the following files:
- http://docs.trilinos.org/r13.0/packages/intrepid/src/Cell/Intrepid_CellTools.hpp
- http://docs.trilinos.org/r13.0/packages/intrepid/src/Cell/Intrepid_CellToolsDef.hpp
 1.8.5
1.8.5