|
Tempus
Version of the Day
Time Integration
|
|
Tempus
Version of the Day
Time Integration
|
Partitioned Implicit-Explicit Runge-Kutta (IMEX-RK) time stepper. More...
#include <Tempus_StepperIMEX_RK_Partition_decl.hpp>
Public Member Functions | |
| StepperIMEX_RK_Partition () | |
| Default constructor. More... | |
| StepperIMEX_RK_Partition (const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > &appModel, Teuchos::RCP< Teuchos::ParameterList > pList) | |
| Constructor to specialize Stepper parameters. More... | |
| StepperIMEX_RK_Partition (const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > &appModel, std::string stepperType="Partitioned IMEX RK SSP2") | |
| Constructor to use default Stepper parameters. More... | |
| StepperIMEX_RK_Partition (const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > &models, std::string stepperType, Teuchos::RCP< Teuchos::ParameterList > pList) | |
| Constructor for StepperFactory. More... | |
| virtual Scalar | getAlpha (const Scalar dt) const |
| Return alpha = d(xDot)/dx. More... | |
| virtual Scalar | getBeta (const Scalar) const |
| Return beta = d(x)/dx. More... | |
| void | evalImplicitModelExplicitly (const Teuchos::RCP< const Thyra::VectorBase< Scalar > > &X, const Teuchos::RCP< const Thyra::VectorBase< Scalar > > &Y, Scalar time, Scalar stepSize, Scalar stageNumber, const Teuchos::RCP< Thyra::VectorBase< Scalar > > &G) const |
| void | evalExplicitModel (const Teuchos::RCP< const Thyra::VectorBase< Scalar > > &X, Scalar time, Scalar stepSize, Scalar stageNumber, const Teuchos::RCP< Thyra::VectorBase< Scalar > > &F) const |
Basic stepper methods | |
| virtual void | setTableaus (Teuchos::RCP< Teuchos::ParameterList > pList, std::string stepperType="") |
| Set both the explicit and implicit tableau from ParameterList. More... | |
| virtual void | setExplicitTableau (std::string stepperType, Teuchos::RCP< Teuchos::ParameterList > pList) |
| Set the explicit tableau from ParameterList. More... | |
| virtual void | setExplicitTableau (Teuchos::RCP< const RKButcherTableau< Scalar > > explicitTableau) |
| Set the explicit tableau from tableau. More... | |
| virtual void | setImplicitTableau (std::string stepperType, Teuchos::RCP< Teuchos::ParameterList > pList) |
| Set the implicit tableau from ParameterList. More... | |
| virtual void | setImplicitTableau (Teuchos::RCP< const RKButcherTableau< Scalar > > implicitTableau) |
| Set the implicit tableau from tableau. More... | |
| virtual void | setModel (const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > &appModel) |
| virtual Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > | getModel () |
| virtual void | setModelPair (const Teuchos::RCP< WrapperModelEvaluatorPairPartIMEX_Basic< Scalar > > &modelPair) |
| Create WrapperModelPairIMEX from user-supplied ModelEvaluator pair. More... | |
| virtual void | setModelPair (const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > &explicitModel, const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > &implicitModel) |
| Create WrapperModelPairIMEX from explicit/implicit ModelEvaluators. More... | |
| virtual void | setObserver (Teuchos::RCP< StepperObserver< Scalar > > obs=Teuchos::null) |
| Set Observer. More... | |
| virtual void | initialize () |
| Initialize during construction and after changing input parameters. More... | |
| virtual void | setInitialConditions (const Teuchos::RCP< SolutionHistory< Scalar > > &solutionHistory) |
| Set the initial conditions and make them consistent. More... | |
| virtual void | takeStep (const Teuchos::RCP< SolutionHistory< Scalar > > &solutionHistory) |
| Take the specified timestep, dt, and return true if successful. More... | |
| virtual Teuchos::RCP < Tempus::StepperState< Scalar > > | getDefaultStepperState () |
| Provide a StepperState to the SolutionState. This Stepper does not have any special state data, so just provide the base class StepperState with the Stepper description. This can be checked to ensure that the input StepperState can be used by this Stepper. More... | |
| virtual Scalar | getOrder () const |
| virtual Scalar | getOrderMin () const |
| virtual Scalar | getOrderMax () const |
| virtual bool | isExplicit () const |
| virtual bool | isImplicit () const |
| virtual bool | isExplicitImplicit () const |
| virtual bool | isOneStepMethod () const |
| virtual bool | isMultiStepMethod () const |
| virtual OrderODE | getOrderODE () const |
ParameterList methods | |
| void | setParameterList (const Teuchos::RCP< Teuchos::ParameterList > &pl) |
| Teuchos::RCP < Teuchos::ParameterList > | getNonconstParameterList () |
| Teuchos::RCP < Teuchos::ParameterList > | unsetParameterList () |
| Teuchos::RCP< const Teuchos::ParameterList > | getValidParameters () const |
| Teuchos::RCP < Teuchos::ParameterList > | getDefaultParameters () const |
Overridden from Teuchos::Describable | |
| virtual std::string | description () const |
| virtual void | describe (Teuchos::FancyOStream &out, const Teuchos::EVerbosityLevel verbLevel) const |
 Public Member Functions inherited from Tempus::StepperImplicit< Scalar > Public Member Functions inherited from Tempus::StepperImplicit< Scalar > | |
| virtual void | setNonConstModel (const Teuchos::RCP< Thyra::ModelEvaluator< Scalar > > &appModel) |
| virtual Teuchos::RCP< const WrapperModelEvaluator< Scalar > > | getWrapperModel () |
| virtual void | setSolver (std::string solverName) |
| Set solver via ParameterList solver name. More... | |
| virtual void | setSolver (Teuchos::RCP< Teuchos::ParameterList > solverPL=Teuchos::null) |
| Set solver via solver ParameterList. More... | |
| virtual void | setSolver (Teuchos::RCP< Thyra::NonlinearSolverBase< Scalar > > solver) |
| Set solver. More... | |
| virtual Teuchos::RCP < Thyra::NonlinearSolverBase < Scalar > > | getSolver () const |
| Get solver. More... | |
| virtual std::string | getStepperType () const |
| const Thyra::SolveStatus< Scalar > | solveImplicitODE (const Teuchos::RCP< Thyra::VectorBase< Scalar > > &x) |
| Solve problem using x in-place. (Needs to be deprecated!) More... | |
| const Thyra::SolveStatus< Scalar > | solveImplicitODE (const Teuchos::RCP< Thyra::VectorBase< Scalar > > &x, const Teuchos::RCP< Thyra::VectorBase< Scalar > > &xDot, const Scalar time, const Teuchos::RCP< ImplicitODEParameters< Scalar > > &p) |
| Solve implicit ODE, f(x, xDot, t, p) = 0. More... | |
| void | evaluateImplicitODE (Teuchos::RCP< Thyra::VectorBase< Scalar > > &f, const Teuchos::RCP< Thyra::VectorBase< Scalar > > &x, const Teuchos::RCP< Thyra::VectorBase< Scalar > > &xDot, const Scalar time, const Teuchos::RCP< ImplicitODEParameters< Scalar > > &p) |
| Evaluate implicit ODE, f(x, xDot, t, p), residual. More... | |
| virtual void | setInitialGuess (Teuchos::RCP< const Thyra::VectorBase< Scalar > > initial_guess) |
| Pass initial guess to Newton solver (only relevant for implicit solvers) More... | |
| virtual void | setZeroInitialGuess (bool zIG) |
| Set parameter so that the initial guess is set to zero (=True) or use last timestep (=False). More... | |
| virtual bool | getZeroInitialGuess () const |
| virtual Scalar | getInitTimeStep (const Teuchos::RCP< SolutionHistory< Scalar > > &) const |
| virtual bool | getEmbedded () const |
| virtual void | setUseFSAL (bool a) |
| virtual bool | getUseFSAL () const |
| virtual void | setICConsistency (std::string s) |
| virtual std::string | getICConsistency () const |
| virtual void | setICConsistencyCheck (bool c) |
| virtual bool | getICConsistencyCheck () const |
| virtual void | setStepperXDot (Teuchos::RCP< Thyra::VectorBase< Scalar > > xDot) |
| Set xDot for Stepper storage. More... | |
| virtual Teuchos::RCP < Thyra::VectorBase< Scalar > > | getStepperXDot (Teuchos::RCP< SolutionState< Scalar > > state) |
| Get xDot from SolutionState or Stepper storage. More... | |
| virtual Teuchos::RCP < Thyra::VectorBase< Scalar > > | getStepperXDotDot (Teuchos::RCP< SolutionState< Scalar > > state) |
| Get xDotDot from SolutionState or Stepper storage. More... | |
 Public Member Functions inherited from Tempus::Stepper< Scalar > Public Member Functions inherited from Tempus::Stepper< Scalar > | |
| virtual void | modelWarning () const |
| void | getValidParametersBasic (Teuchos::RCP< Teuchos::ParameterList > pl) const |
| virtual void | createSubSteppers (std::vector< Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > >) |
| void | validExplicitODE (const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > &model) const |
| Validate that the model supports explicit ODE evaluation, f(x,t) [=xdot]. More... | |
| void | validSecondOrderExplicitODE (const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > &model) const |
| Validate that the model supports explicit second order ODE evaluation, f(x,xdot,t) [=xdotdot]. More... | |
| void | validImplicitODE_DAE (const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > &model) const |
| Validate ME supports implicit ODE/DAE evaluation, f(xdot,x,t) [= 0]. More... | |
| void | validSecondOrderODE_DAE (const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > &model) const |
| Validate ME supports 2nd order implicit ODE/DAE evaluation, f(xdotdot,xdot,x,t) [= 0]. More... | |
| Teuchos::RCP < Teuchos::ParameterList > | defaultSolverParameters () const |
Protected Attributes | |
| std::string | description_ |
| Teuchos::RCP< const RKButcherTableau< Scalar > > | explicitTableau_ |
| Teuchos::RCP< const RKButcherTableau< Scalar > > | implicitTableau_ |
| Scalar | order_ |
| Teuchos::RCP < Thyra::VectorBase< Scalar > > | stageZ_ |
| std::vector< Teuchos::RCP < Thyra::VectorBase< Scalar > > > | stageF_ |
| std::vector< Teuchos::RCP < Thyra::VectorBase< Scalar > > > | stageGx_ |
| Teuchos::RCP < Thyra::VectorBase< Scalar > > | xTilde_ |
| Teuchos::RCP < StepperIMEX_RKPartObserver < Scalar > > | stepperIMEX_RKPartObserver_ |
 Protected Attributes inherited from Tempus::StepperImplicit< Scalar > Protected Attributes inherited from Tempus::StepperImplicit< Scalar > | |
| Teuchos::RCP < Teuchos::ParameterList > | stepperPL_ |
| Teuchos::RCP < WrapperModelEvaluator < Scalar > > | wrapperModel_ |
| Teuchos::RCP < Thyra::NonlinearSolverBase < Scalar > > | solver_ |
| Teuchos::RCP< const Thyra::VectorBase< Scalar > > | initial_guess_ |
| Teuchos::RCP< StepperObserver < Scalar > > | stepperObserver_ |
| Teuchos::RCP < Thyra::VectorBase< Scalar > > | stepperXDot_ |
| Teuchos::RCP < Thyra::VectorBase< Scalar > > | stepperXDotDot_ |
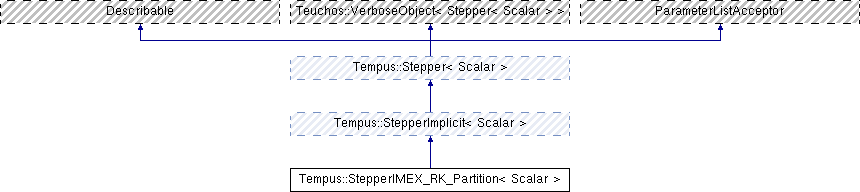
Partitioned Implicit-Explicit Runge-Kutta (IMEX-RK) time stepper.
Partitioned IMEX-RK is similar to the IMEX-RK (StepperIMEX_RK), except a portion of the solution only requires explicit integration, and should not be part of the implicit solution to reduce computational costs. Again our ODE can be written as
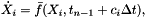
but now
![\[ z =\left\{\begin{array}{c} y\\ x \end{array}\right\},\; F(z,t)=\left\{\begin{array}{c} F^y(x,y,t)\\ F^x(x,y,t)\end{array}\right\}, \mbox{ and } G(z,t)=\left\{\begin{array}{c} 0\\ G^x(x,y,t) \end{array}\right\} \]](form_153.png)
where 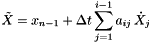 is the product vector of
is the product vector of 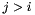 and
and 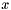 ,
, 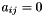 is still the "slow" physics (and evolved explicitly), and
is still the "slow" physics (and evolved explicitly), and 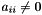 is still the "fast" physics (and evolved implicitly), but a portion of the solution vector,
is still the "fast" physics (and evolved implicitly), but a portion of the solution vector, 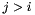 , is "explicit-only" and is only evolved by
, is "explicit-only" and is only evolved by 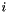 , while
, while 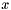 is the Implicit/Explicit (IMEX) solution vector, and is evolved explicitly by
is the Implicit/Explicit (IMEX) solution vector, and is evolved explicitly by 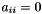 evolved implicitly by
evolved implicitly by 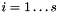 . Note we can expand this to explicitly show all the terms as
. Note we can expand this to explicitly show all the terms as
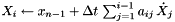
or
![\[ \left\{ \begin{array}{c} \dot{y} \\ \dot{x} \end{array}\right\} + \left\{ \begin{array}{c} f^y \\ f^x \end{array}\right\} + \left\{ \begin{array}{c} 0 \\ g^x \end{array}\right\} = 0 \]](form_162.png)
where 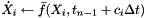 ,
, 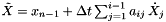 , and
, and 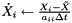 , or
, or
![\[ \dot{z} + f(x,y,t) + g(x,y,t) = 0, \]](form_166.png)
where 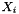 , and
, and 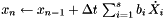 . Using Butcher tableaus for the explicit terms
. Using Butcher tableaus for the explicit terms
![\[ \begin{array}{c|c} \hat{c} & \hat{A} \\ \hline & \hat{b}^T \end{array} \;\;\;\; \mbox{ and for implicit terms } \;\;\;\; \begin{array}{c|c} c & A \\ \hline & b^T \end{array}, \]](form_112.png)
the basic scheme for this partitioned, 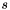 -stage, IMEX-RK is
-stage, IMEX-RK is
![\[ \begin{array}{rcll} Z_i & = & Z_{n-1} - \Delta t \sum_{j=1}^{i-1} \hat{a}_{ij}\; f(Z_j,\hat{t}_j) - \Delta t \sum_{j=1}^i a_{ij}\; g(Z_j, t_j) & \mbox{for } i=1\ldots s, \\ z_n & = & z_{n-1} - \Delta t \sum_{i=1}^s \left[ \hat{b}_i\; f(Z_i,\hat{t}_i) + b_i\; g(Z_i, t_i) \right] & \end{array} \]](form_169.png)
or expanded
![\[ \begin{array}{rcll} Y_i & = & y_{n-1} - \Delta t \sum_{j=1}^{i-1} \hat{a}_{ij}\; f^y(Z_j,\hat{t}_j) & \mbox{for } i=1\ldots s,\\ X_i & = & x_{n-1} - \Delta t \sum_{j=1}^{i-1} \hat{a}_{ij}\; f^x(Z_j,\hat{t}_j) - \Delta t \sum_{j=1}^i a_{ij}\; g^x(Z_j, t_j) & \mbox{for } i=1\ldots s, \\ y_n & = & y_{n-1} - \Delta t \sum_{i=1}^s \hat{b}_{i}\; f^y(X_i,Y_i,\hat{t}_i) & \\ x_n & = & x_{n-1} - \Delta t \sum_{i=1}^s \left[ \hat{b}_i\; f^x(Z_i,\hat{t}_i) + b_i\; g^x(Z_i, t_i) \right] & \end{array} \]](form_170.png)
where 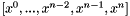 and
and 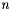 .
.
For iterative solvers, it is useful to write the stage solutions as
![\[ Z_i = \tilde{Z} - a_{ii} \Delta t\, g(Z_i,t_i) \]](form_171.png)
or expanded as
![\[ \left\{ \begin{array}{c} Y_i \\ X_i \end{array}\right\} = \left\{ \begin{array}{c} \tilde{Y} \\ \tilde{X}_i \end{array}\right\} - a_{ii} \Delta t \left\{ \begin{array}{c} 0 \\ g^x(Z_i,t_i) \end{array}\right\} \]](form_172.png)
where
![\begin{eqnarray*} \tilde{Z} & = & z_{n-1} - \Delta t \sum_{j=1}^{i-1} \left[\hat{a}_{ij}\, f(Z_j,\hat{t}_j) + a_{ij}\, g(Z_j, t_j)\right] \\ \tilde{Y} & = & y_{n-1} - \Delta t \sum_{j=1}^{i-1} \left[\hat{a}_{ij}\, f^y(Z_j,\hat{t}_j)\right] \\ \tilde{X} & = & x_{n-1} - \Delta t \sum_{j=1}^{i-1} \left[\hat{a}_{ij}\, f^x(Z_j,\hat{t}_j) +a_{ij}\, g^x(Z_j,t_j)\right] \\ \end{eqnarray*}](form_173.png)
and note that 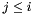 . Rearranging to solve for the implicit term
. Rearranging to solve for the implicit term
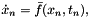
We additionally need the time derivative at each stage for the implicit solve. Let us define the following time derivative for 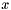 portion of the solution
portion of the solution
![\[ \dot{X}_i(X_i,Y_i,t_i) + f^x(X_i,Y_i,t_i) + g^x(X_i,Y_i,t_i) = 0 \]](form_176.png)
where we split 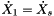 arguments into
arguments into 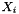 and
and 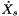 to emphasize that
to emphasize that 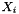 is the solution for the implicit solve and
is the solution for the implicit solve and 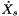 are parameters in this set of equations. The above time derivative,
are parameters in this set of equations. The above time derivative,  , is NOT likely the same as the real time derivative,
, is NOT likely the same as the real time derivative,  , unless
, unless 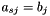 (Reasoning:
(Reasoning: 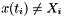 and
and 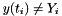 unless
unless 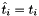 ). Also note that the explicit term,
). Also note that the explicit term, 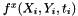 , is evaluated at the implicit stage time,
, is evaluated at the implicit stage time, 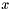 .
.
We can form the time derivative
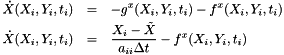
Returning to the governing equation for the IMEX solution vector, 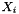
![\begin{eqnarray*} M^x(X_i,Y_i,t_i)\, \dot{X}(X_i,Y_i,t_i) + F^x(X_i,Y_i,t_i) + G^x(X_i,Y_i,t_i) & = & 0 \\ M^x(X_i,Y_i,t_i)\, \left[ \frac{X_i - \tilde{X}}{a_{ii} \Delta t} - f^x(X_i,Y_i,t_i) \right] + F^x(X_i,Y_i,t_i) + G^x(X_i,Y_i,t_i) & = & 0 \\ M^x(X_i,Y_i,t_i)\, \left[ \frac{X_i - \tilde{X}}{a_{ii} \Delta t} \right] + G(X_i,Y_i,t_i) & = & 0 \\ \end{eqnarray*}](form_187.png)
Recall 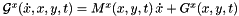 and if we define a pseudo time derivative, which is equivalent to the time derivative for the implicit solve,
and if we define a pseudo time derivative, which is equivalent to the time derivative for the implicit solve,
![\[ \tilde{\dot{X}} = \frac{X_i - \tilde{X}}{a_{ii} \Delta t}, \]](form_189.png)
we can write
![\[ \mathcal{G}^x(\tilde{\dot{X}},X_i,Y_i,t_i) = M^x(X_i,Y_i,t_i)\, \tilde{\dot{X}} + G^x(X_i,Y_i,t_i) = 0 \]](form_190.png)
For general DIRK methods, we need to also handle the case when 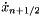 . The IMEX stage values can be simply evaluated similiar to the "explicit-only" stage values, e.g.,
. The IMEX stage values can be simply evaluated similiar to the "explicit-only" stage values, e.g.,
![\[ X_i = \tilde{X} = x_{n-1} - \Delta t\,\sum_{j=1}^{i-1} \left( \hat{a}_{ij}\, f^x_j + a_{ij}\, g^x_j \right) \]](form_191.png)
and then we can simply evaluate
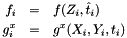
We can then form the time derivative as
![\[ \dot{X}_i = - g^x(X_i,Y_i,t_i) - f^x(X_i,Y_i,t_i) \]](form_193.png)
but again note that the explicit term, 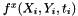 , is evaluated at the implicit stage time,
, is evaluated at the implicit stage time, 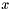 .
.
Partitioned IMEX-RK Algorithm The single-timestep algorithm for the partitioned IMEX-RK is
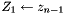 (Recall
(Recall 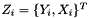 )
)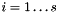 do
do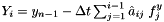
![$\tilde{X} \leftarrow x_{n-1} - \Delta t\,\sum_{j=1}^{i-1} \left[ \hat{a}_{ij}\, f^x_j + a_{ij}\, g^x_j \right] $](form_197.png)
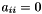
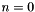
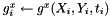
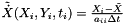
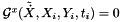 for
for 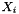 where
where 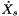 are known parameters
are known parameters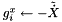
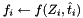
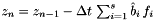
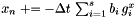
The First-Step-As-Last (FSAL) principle is not valid for IMEX RK Partition. The default is to set useFSAL=false, and useFSAL=true will result in an error.
Definition at line 227 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
| Tempus::StepperIMEX_RK_Partition< Scalar >::StepperIMEX_RK_Partition | ( | ) |
Default constructor.
Definition at line 28 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
| Tempus::StepperIMEX_RK_Partition< Scalar >::StepperIMEX_RK_Partition | ( | const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > & | appModel, |
| Teuchos::RCP< Teuchos::ParameterList > | pList | ||
| ) |
Constructor to specialize Stepper parameters.
Definition at line 37 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
| Tempus::StepperIMEX_RK_Partition< Scalar >::StepperIMEX_RK_Partition | ( | const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > & | appModel, |
| std::string | stepperType = "Partitioned IMEX RK SSP2" |
||
| ) |
Constructor to use default Stepper parameters.
Definition at line 55 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
| Tempus::StepperIMEX_RK_Partition< Scalar >::StepperIMEX_RK_Partition | ( | const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > & | models, |
| std::string | stepperType, | ||
| Teuchos::RCP< Teuchos::ParameterList > | pList | ||
| ) |
Constructor for StepperFactory.
Definition at line 72 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Definition at line 717 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Definition at line 710 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
| void Tempus::StepperIMEX_RK_Partition< Scalar >::evalExplicitModel | ( | const Teuchos::RCP< const Thyra::VectorBase< Scalar > > & | X, |
| Scalar | time, | ||
| Scalar | stepSize, | ||
| Scalar | stageNumber, | ||
| const Teuchos::RCP< Thyra::VectorBase< Scalar > > & | F | ||
| ) | const |
Definition at line 499 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
| void Tempus::StepperIMEX_RK_Partition< Scalar >::evalImplicitModelExplicitly | ( | const Teuchos::RCP< const Thyra::VectorBase< Scalar > > & | X, |
| const Teuchos::RCP< const Thyra::VectorBase< Scalar > > & | Y, | ||
| Scalar | time, | ||
| Scalar | stepSize, | ||
| Scalar | stageNumber, | ||
| const Teuchos::RCP< Thyra::VectorBase< Scalar > > & | G | ||
| ) | const |
Definition at line 464 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
inlinevirtual |
Return alpha = d(xDot)/dx.
Implements Tempus::StepperImplicit< Scalar >.
Definition at line 321 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
inlinevirtual |
Return beta = d(x)/dx.
Implements Tempus::StepperImplicit< Scalar >.
Definition at line 327 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
virtual |
Implements Tempus::Stepper< Scalar >.
Definition at line 760 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Provide a StepperState to the SolutionState. This Stepper does not have any special state data, so just provide the base class StepperState with the Stepper description. This can be checked to ensure that the input StepperState can be used by this Stepper.
Implements Tempus::Stepper< Scalar >.
Definition at line 701 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
inlinevirtual |
Reimplemented from Tempus::StepperImplicit< Scalar >.
Definition at line 280 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
| Teuchos::RCP< Teuchos::ParameterList > Tempus::StepperIMEX_RK_Partition< Scalar >::getNonconstParameterList | ( | ) |
Definition at line 778 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
inlinevirtual |
Implements Tempus::Stepper< Scalar >.
Definition at line 306 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
inlinevirtual |
Implements Tempus::Stepper< Scalar >.
Definition at line 308 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
inlinevirtual |
Implements Tempus::Stepper< Scalar >.
Definition at line 307 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
inlinevirtual |
Implements Tempus::Stepper< Scalar >.
Definition at line 317 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
| Teuchos::RCP< const Teuchos::ParameterList > Tempus::StepperIMEX_RK_Partition< Scalar >::getValidParameters | ( | ) | const |
Definition at line 744 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Initialize during construction and after changing input parameters.
Implements Tempus::Stepper< Scalar >.
Definition at line 374 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
inlinevirtual |
Implements Tempus::Stepper< Scalar >.
Definition at line 310 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
inlinevirtual |
Implements Tempus::Stepper< Scalar >.
Definition at line 312 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
inlinevirtual |
Implements Tempus::Stepper< Scalar >.
Definition at line 311 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
inlinevirtual |
Implements Tempus::Stepper< Scalar >.
Definition at line 315 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
inlinevirtual |
Implements Tempus::Stepper< Scalar >.
Definition at line 314 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
virtual |
Set the explicit tableau from ParameterList.
Definition at line 246 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Set the explicit tableau from tableau.
Definition at line 257 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Set the implicit tableau from ParameterList.
Definition at line 269 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Set the implicit tableau from tableau.
Definition at line 280 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Set the initial conditions and make them consistent.
Reimplemented from Tempus::StepperImplicit< Scalar >.
Definition at line 416 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Reimplemented from Tempus::StepperImplicit< Scalar >.
Definition at line 291 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Create WrapperModelPairIMEX from user-supplied ModelEvaluator pair.
The user-supplied ME pair can contain any user-specific IMEX interactions between explicit and implicit MEs.
Definition at line 317 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Create WrapperModelPairIMEX from explicit/implicit ModelEvaluators.
Use the supplied explicit/implicit MEs to create a WrapperModelPairIMEX with basic IMEX interactions between explicit and implicit MEs.
Definition at line 339 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Set Observer.
Implements Tempus::Stepper< Scalar >.
Definition at line 352 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
| void Tempus::StepperIMEX_RK_Partition< Scalar >::setParameterList | ( | const Teuchos::RCP< Teuchos::ParameterList > & | pl | ) |
Definition at line 728 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Set both the explicit and implicit tableau from ParameterList.
Definition at line 91 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
virtual |
Take the specified timestep, dt, and return true if successful.
Implements Tempus::Stepper< Scalar >.
Definition at line 535 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
| Teuchos::RCP< Teuchos::ParameterList > Tempus::StepperIMEX_RK_Partition< Scalar >::unsetParameterList | ( | ) |
Definition at line 786 of file Tempus_StepperIMEX_RK_Partition_impl.hpp.
|
protected |
Definition at line 358 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
protected |
Definition at line 359 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
protected |
Definition at line 360 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
protected |
Definition at line 362 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
protected |
Definition at line 365 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
protected |
Definition at line 366 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
protected |
Definition at line 364 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
protected |
Definition at line 370 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.
|
protected |
Definition at line 368 of file Tempus_StepperIMEX_RK_Partition_decl.hpp.