Implementation of the default H(curl)-compatible FEM basis of degree 1 on Hexahedron cell. More...
#include <Intrepid_HCURL_HEX_I1_FEM.hpp>
Inheritance diagram for Intrepid::Basis_HCURL_HEX_I1_FEM< Scalar, ArrayScalar >:

Public Member Functions | |
| Basis_HCURL_HEX_I1_FEM () | |
| Constructor. | |
| void | getValues (ArrayScalar &outputValues, const ArrayScalar &inputPoints, const EOperator operatorType) const |
| Evaluation of a FEM basis on a reference Hexahedron cell. More... | |
| void | getValues (ArrayScalar &outputValues, const ArrayScalar &inputPoints, const ArrayScalar &cellVertices, const EOperator operatorType=OPERATOR_VALUE) const |
| FVD basis evaluation: invocation of this method throws an exception. | |
| void | getDofCoords (ArrayScalar &DofCoords) const |
| Returns spatial locations (coordinates) of degrees of freedom on a reference Quadrilateral. More... | |
 Public Member Functions inherited from Intrepid::Basis< Scalar, ArrayScalar > Public Member Functions inherited from Intrepid::Basis< Scalar, ArrayScalar > | |
| virtual | ~Basis () |
| Destructor. | |
| virtual int | getCardinality () const |
| Returns cardinality of the basis. More... | |
| virtual int | getDegree () const |
| Returns the degree of the basis. More... | |
| virtual const shards::CellTopology | getBaseCellTopology () const |
| Returns the base cell topology for which the basis is defined. See Shards documentation http://trilinos.sandia.gov/packages/shards for definition of base cell topology. More... | |
| virtual EBasis | getBasisType () const |
| Returns the basis type. More... | |
| virtual ECoordinates | getCoordinateSystem () const |
| Returns the type of coordinate system for which the basis is defined. More... | |
| virtual int | getDofOrdinal (const int subcDim, const int subcOrd, const int subcDofOrd) |
| DoF tag to ordinal lookup. More... | |
|
virtual const std::vector < std::vector< std::vector < int > > > & | getDofOrdinalData () |
| DoF tag to ordinal data structure. | |
| virtual const std::vector< int > & | getDofTag (const int dofOrd) |
| DoF ordinal to DoF tag lookup. More... | |
| virtual const std::vector < std::vector< int > > & | getAllDofTags () |
| Retrieves all DoF tags. More... | |
 Public Member Functions inherited from Intrepid::DofCoordsInterface< ArrayScalar > Public Member Functions inherited from Intrepid::DofCoordsInterface< ArrayScalar > | |
| virtual | ~DofCoordsInterface ()=0 |
| Pure virtual destructor (gives warnings if not included). Following "Effective C++: 3rd Ed." item 7 the implementation is included in the definition file. | |
Private Member Functions | |
| void | initializeTags () |
| Initializes tagToOrdinal_ and ordinalToTag_ lookup arrays. | |
Additional Inherited Members | |
 Protected Attributes inherited from Intrepid::Basis< Scalar, ArrayScalar > Protected Attributes inherited from Intrepid::Basis< Scalar, ArrayScalar > | |
| int | basisCardinality_ |
| Cardinality of the basis, i.e., the number of basis functions/degrees-of-freedom. | |
| int | basisDegree_ |
| Degree of the largest complete polynomial space that can be represented by the basis. | |
| shards::CellTopology | basisCellTopology_ |
| Base topology of the cells for which the basis is defined. See the Shards package http://trilinos.sandia.gov/packages/shards for definition of base cell topology. | |
| EBasis | basisType_ |
| Type of the basis. | |
| ECoordinates | basisCoordinates_ |
| The coordinate system for which the basis is defined. | |
| bool | basisTagsAreSet_ |
| "true" if tagToOrdinal_ and ordinalToTag_ have been initialized | |
| std::vector< std::vector< int > > | ordinalToTag_ |
| DoF ordinal to tag lookup table. More... | |
| std::vector< std::vector < std::vector< int > > > | tagToOrdinal_ |
| DoF tag to ordinal lookup table. More... | |
Detailed Description
template<class Scalar, class ArrayScalar>
class Intrepid::Basis_HCURL_HEX_I1_FEM< Scalar, ArrayScalar >
Implementation of the default H(curl)-compatible FEM basis of degree 1 on Hexahedron cell.
Implements Nedelec basis of degree 1 on the reference Hexahedron cell. The basis has
cardinality 12 and spans an INCOMPLETE tri-linear polynomial space. Basis functions are dual
to a unisolvent set of degrees-of-freedom (DoF) defined and enumerated as follows:
=================================================================================================== | | degree-of-freedom-tag table | | | DoF |----------------------------------------------------------| DoF definition | | ordinal | subc dim | subc ordinal | subc DoF ord |subc num DoF | | |=========|==============|==============|==============|=============|============================| | 0 | 1 | 0 | 0 | 1 | L_0(u) = (u.t)(0,-1,-1) | |---------|--------------|--------------|--------------|-------------|----------------------------| | 1 | 1 | 1 | 0 | 1 | L_1(u) = (u.t)(1,0,-1) | |---------|--------------|--------------|--------------|-------------|----------------------------| | 2 | 1 | 2 | 0 | 1 | L_2(u) = (u.t)(0,1,-1) | |---------|--------------|--------------|--------------|-------------|----------------------------| | 3 | 1 | 3 | 0 | 1 | L_3(u) = (u.t)(-1,0,-1) | |---------|--------------|--------------|--------------|-------------|----------------------------| | 4 | 1 | 4 | 0 | 1 | L_4(u) = (u.t)(0,-1,1) | |---------|--------------|--------------|--------------|-------------|----------------------------| | 5 | 1 | 5 | 0 | 1 | L_5(u) = (u.t)(1,0,1) | |---------|--------------|--------------|--------------|-------------|----------------------------| | 6 | 1 | 6 | 0 | 1 | L_6(u) = (u.t)(0,1,1) | |---------|--------------|--------------|--------------|-------------|----------------------------| | 7 | 1 | 7 | 0 | 1 | L_7(u) = (u.t)(-1,0,1) | |---------|--------------|--------------|--------------|-------------|----------------------------| | 8 | 1 | 8 | 0 | 1 | L_8(u) = (u.t)(-1,-1,0) | |---------|--------------|--------------|--------------|-------------|----------------------------| | 9 | 1 | 9 | 0 | 1 | L_9(u) = (u.t)(1,-1,0) | |---------|--------------|--------------|--------------|-------------|----------------------------| | 10 | 1 | 10 | 0 | 1 | L_10(u) = (u.t)(1,1,0) | |---------|--------------|--------------|--------------|-------------|----------------------------| | 11 | 1 | 11 | 0 | 1 | L_11(u) = (u.t)(-1,1,0) | |=========|==============|==============|==============|=============|============================| | MAX | maxScDim=1 | maxScOrd=11 | maxDfOrd=0 | - | | |=========|==============|==============|==============|=============|============================|
- Remarks
- In the DoF functional
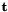 is an edge tangent. Direction of edge tangents follows the vertex order of the edges in the cell topology and runs from edge vertex 0 to edge vertex 1, whereas their length is set equal to edge length. For example, edge 8 of all Hexahedron reference cells has vertex order {0,4}, i.e., its tangent runs from vertex 0 of the reference Hexahedron to vertex 4 of that cell. On the reference Hexahedron the coordinates of these vertices are (-1,-1,-1) and (-1,-1,1), respectively. Therefore, the tangent to edge 8 is (-1,-1, 1) - (-1,-1,-1) = (0, 0, 2). Because its length already equals edge length, no further rescaling of the edge tangent is needed.
is an edge tangent. Direction of edge tangents follows the vertex order of the edges in the cell topology and runs from edge vertex 0 to edge vertex 1, whereas their length is set equal to edge length. For example, edge 8 of all Hexahedron reference cells has vertex order {0,4}, i.e., its tangent runs from vertex 0 of the reference Hexahedron to vertex 4 of that cell. On the reference Hexahedron the coordinates of these vertices are (-1,-1,-1) and (-1,-1,1), respectively. Therefore, the tangent to edge 8 is (-1,-1, 1) - (-1,-1,-1) = (0, 0, 2). Because its length already equals edge length, no further rescaling of the edge tangent is needed.
- The length of the edge tangent equals the edge length. As a result, the DoF functional is the value of the tangent component of a vector field at the edge midpoint times the edge length. The resulting basis is equivalent to a basis defined by using the edge circulation as a DoF functional. Note that all edges of reference Hexahedron<> cells have length 2.
- In the DoF functional
Definition at line 115 of file Intrepid_HCURL_HEX_I1_FEM.hpp.
Member Function Documentation
template<class Scalar , class ArrayScalar >
|
virtual |
Returns spatial locations (coordinates) of degrees of freedom on a reference Quadrilateral.
- Parameters
-
DofCoords [out] - array with the coordinates of degrees of freedom, dimensioned (F,D)
Implements Intrepid::DofCoordsInterface< ArrayScalar >.
Definition at line 302 of file Intrepid_HCURL_HEX_I1_FEMDef.hpp.
template<class Scalar , class ArrayScalar >
|
virtual |
Evaluation of a FEM basis on a reference Hexahedron cell.
Returns values of <var>operatorType</var> acting on FEM basis functions for a set of
points in the <strong>reference Hexahedron</strong> cell. For rank and dimensions of
I/O array arguments see Section \ref basis_md_array_sec.
- Parameters
-
outputValues [out] - rank-3 array with the computed basis values inputPoints [in] - rank-2 array with dimensions (P,D) containing reference points operatorType [in] - operator applied to basis functions
Implements Intrepid::Basis< Scalar, ArrayScalar >.
Definition at line 100 of file Intrepid_HCURL_HEX_I1_FEMDef.hpp.
The documentation for this class was generated from the following files:
- http://docs.trilinos.org/r13.0/packages/intrepid/src/Discretization/Basis/Intrepid_HCURL_HEX_I1_FEM.hpp
- http://docs.trilinos.org/r13.0/packages/intrepid/src/Discretization/Basis/Intrepid_HCURL_HEX_I1_FEMDef.hpp
 1.8.5
1.8.5