Utility class that provides methods for higher-order algebraic manipulation of user-defined arrays, such as tensor contractions. For low-order operations, see Intrepid::RealSpaceTools. More...
#include <Intrepid_ArrayTools.hpp>
Classes | |
| struct | cloneFields2 |
| struct | matmatProductDataDataTempSpecLeft |
| struct | matmatProductDataDataTempSpecRight |
| struct | scalarMultiplyDataData2 |
| There are two use cases: (1) dot product of a rank-3, 4 or 5 container inputFields with dimensions (C,F,P) (C,F,P,D1) or (C,F,P,D1,D2), representing the values of a set of scalar, vector or tensor fields, by the values in a rank-2, 3 or 4 container inputData indexed by (C,P), (C,P,D1), or (C,P,D1,D2) representing the values of scalar, vector or tensor data, OR (2) dot product of a rank-2, 3 or 4 container inputFields with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or tensor field, by the values in a rank-2 container inputData indexed by (C,P), (C,P,D1) or (C,P,D1,D2), representing the values of scalar, vector or tensor data; the output value container outputFields is indexed by (C,F,P), regardless of which of the two use cases is considered. More... | |
| struct | scalarMultiplyDataField2 |
Static Public Member Functions | |
| template<class Scalar , class ArrayOutFields , class ArrayInFieldsLeft , class ArrayInFieldsRight > | |
| static void | contractFieldFieldScalar (ArrayOutFields &outputFields, const ArrayInFieldsLeft &leftFields, const ArrayInFieldsRight &rightFields, const ECompEngine compEngine, const bool sumInto=false) |
| Contracts the "point" dimension P of two rank-3 containers with dimensions (C,L,P) and (C,R,P), and returns the result in a rank-3 container with dimensions (C,L,R). More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInFieldsLeft , class ArrayInFieldsRight > | |
| static void | contractFieldFieldVector (ArrayOutFields &outputFields, const ArrayInFieldsLeft &leftFields, const ArrayInFieldsRight &rightFields, const ECompEngine compEngine, const bool sumInto=false) |
| Contracts the "point" and "space" dimensions P and D1 of two rank-4 containers with dimensions (C,L,P,D1) and (C,R,P,D1), and returns the result in a rank-3 container with dimensions (C,L,R). More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInFieldsLeft , class ArrayInFieldsRight > | |
| static void | contractFieldFieldTensor (ArrayOutFields &outputFields, const ArrayInFieldsLeft &leftFields, const ArrayInFieldsRight &rightFields, const ECompEngine compEngine, const bool sumInto=false) |
| Contracts the "point" and "space" dimensions P, D1, and D2 of two rank-5 containers with dimensions (C,L,P,D1,D2) and (C,R,P,D1,D2), and returns the result in a rank-3 container with dimensions (C,L,R). More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | contractDataFieldScalar (ArrayOutFields &outputFields, const ArrayInData &inputData, const ArrayInFields &inputFields, const ECompEngine compEngine, const bool sumInto=false) |
| Contracts the "point" dimensions P of a rank-3 containers and a rank-2 container with dimensions (C,F,P) and (C,P), respectively, and returns the result in a rank-2 container with dimensions (C,F). More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | contractDataFieldVector (ArrayOutFields &outputFields, const ArrayInData &inputData, const ArrayInFields &inputFields, const ECompEngine compEngine, const bool sumInto=false) |
| Contracts the "point" and "space" dimensions P and D of a rank-4 container and a rank-3 container with dimensions (C,F,P,D) and (C,P,D), respectively, and returns the result in a rank-2 container with dimensions (C,F). More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | contractDataFieldTensor (ArrayOutFields &outputFields, const ArrayInData &inputData, const ArrayInFields &inputFields, const ECompEngine compEngine, const bool sumInto=false) |
| Contracts the "point" and "space" dimensions P, D1 and D2 of a rank-5 container and a rank-4 container with dimensions (C,F,P,D1,D2) and (C,P,D1,D2), respectively, and returns the result in a rank-2 container with dimensions (C,F). More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | contractDataDataScalar (ArrayOutData &outputData, const ArrayInDataLeft &inputDataLeft, const ArrayInDataRight &inputDataRight, const ECompEngine compEngine, const bool sumInto=false) |
| Contracts the "point" dimensions P of rank-2 containers with dimensions (C,P), and returns the result in a rank-1 container with dimensions (C). More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | contractDataDataVector (ArrayOutData &outputData, const ArrayInDataLeft &inputDataLeft, const ArrayInDataRight &inputDataRight, const ECompEngine compEngine, const bool sumInto=false) |
| Contracts the "point" and "space" dimensions P and D of rank-3 containers with dimensions (C,P,D) and returns the result in a rank-1 container with dimensions (C). More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | contractDataDataTensor (ArrayOutData &outputData, const ArrayInDataLeft &inputDataLeft, const ArrayInDataRight &inputDataRight, const ECompEngine compEngine, const bool sumInto=false) |
| Contracts the "point" and "space" dimensions P, D1 and D2 of rank-4 containers with dimensions (C,P,D1,D2) and returns the result in a rank-1 container with dimensions (C). More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | scalarMultiplyDataField (ArrayOutFields &outputFields, const ArrayInData &inputData, const ArrayInFields &inputFields, const bool reciprocal=false) |
| There are two use cases: (1) multiplies a rank-3, 4, or 5 container inputFields with dimensions (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2), representing the values of a set of scalar, vector or tensor fields, by the values in a rank-2 container inputData indexed by (C,P), representing the values of scalar data, OR (2) multiplies a rank-2, 3, or 4 container inputFields with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or a tensor field, by the values in a rank-2 container inputData indexed by (C,P), representing the values of scalar data; the output value container outputFields is indexed by (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2), regardless of which of the two use cases is considered. More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | scalarMultiplyDataData (ArrayOutData &outputData, const ArrayInDataLeft &inputDataLeft, const ArrayInDataRight &inputDataRight, const bool reciprocal=false) |
| There are two use cases: (1) multiplies a rank-2, 3, or 4 container inputDataRight with dimensions (C,P), (C,P,D1) or (C,P,D1,D2), representing the values of a set of scalar, vector or tensor data, by the values in a rank-2 container inputDataLeft indexed by (C,P), representing the values of scalar data, OR (2) multiplies a rank-1, 2, or 3 container inputDataRight with dimensions (P), (P,D1) or (P,D1,D2), representing the values of scalar, vector or tensor data, by the values in a rank-2 container inputDataLeft indexed by (C,P), representing the values of scalar data; the output value container outputData is indexed by (C,P), (C,P,D1) or (C,P,D1,D2), regardless of which of the two use cases is considered. More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | dotMultiplyDataField (ArrayOutFields &outputFields, const ArrayInData &inputDataLeft, const ArrayInFields &inputFields) |
| There are two use cases: (1) dot product of a rank-3, 4 or 5 container inputFields with dimensions (C,F,P) (C,F,P,D1) or (C,F,P,D1,D2), representing the values of a set of scalar, vector or tensor fields, by the values in a rank-2, 3 or 4 container inputData indexed by (C,P), (C,P,D1), or (C,P,D1,D2) representing the values of scalar, vector or tensor data, OR (2) dot product of a rank-2, 3 or 4 container inputFields with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or tensor field, by the values in a rank-2 container inputData indexed by (C,P), (C,P,D1) or (C,P,D1,D2), representing the values of scalar, vector or tensor data; the output value container outputFields is indexed by (C,F,P), regardless of which of the two use cases is considered. More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | dotMultiplyDataData (ArrayOutData &outputData, const ArrayInDataLeft &inputDataLeft, const ArrayInDataRight &inputDataRight) |
| There are two use cases: (1) dot product of a rank-2, 3 or 4 container inputDataRight with dimensions (C,P) (C,P,D1) or (C,P,D1,D2), representing the values of a scalar, vector or a tensor set of data, by the values in a rank-2, 3 or 4 container inputDataLeft indexed by (C,P), (C,P,D1), or (C,P,D1,D2) representing the values of scalar, vector or tensor data, OR (2) dot product of a rank-2, 3 or 4 container inputDataRight with dimensions (P), (P,D1) or (P,D1,D2), representing the values of scalar, vector or tensor data, by the values in a rank-2 container inputDataLeft indexed by (C,P), (C,P,D1) or (C,P,D1,D2), representing the values of scalar, vector, or tensor data; the output value container outputData is indexed by (C,P), regardless of which of the two use cases is considered. More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | crossProductDataField (ArrayOutFields &outputFields, const ArrayInData &inputData, const ArrayInFields &inputFields) |
| There are two use cases: (1) cross product of a rank-4 container inputFields with dimensions (C,F,P,D), representing the values of a set of vector fields, on the left by the values in a rank-3 container inputData indexed by (C,P,D), representing the values of vector data, OR (2) cross product of a rank-3 container inputFields with dimensions (F,P,D), representing the values of a vector field, on the left by the values in a rank-3 container inputData indexed by (C,P,D), representing the values of vector data; the output value container outputFields is indexed by (C,F,P,D) in 3D (vector output) and by (C,F,P) in 2D (scalar output), regardless of which of the two use cases is considered. More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | crossProductDataData (ArrayOutData &outputData, const ArrayInDataLeft &inputDataLeft, const ArrayInDataRight &inputDataRight) |
| There are two use cases: (1) cross product of a rank-3 container inputDataRight with dimensions (C,P,D), representing the values of a set of vector data, on the left by the values in a rank-3 container inputDataLeft indexed by (C,P,D) representing the values of vector data, OR (2) cross product of a rank-2 container inputDataRight with dimensions (P,D), representing the values of vector data, on the left by the values in a rank-3 container inputDataLeft indexed by (C,P,D), representing the values of vector data; the output value container outputData is indexed by (C,P,D) in 3D (vector output) and by (C,P) in 2D (scalar output), regardless of which of the two use cases is considered. More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | outerProductDataField (ArrayOutFields &outputFields, const ArrayInData &inputData, const ArrayInFields &inputFields) |
| There are two use cases: (1) outer product of a rank-4 container inputFields with dimensions (C,F,P,D), representing the values of a set of vector fields, on the left by the values in a rank-3 container inputData indexed by (C,P,D), representing the values of vector data, OR (2) outer product of a rank-3 container inputFields with dimensions (F,P,D), representing the values of a vector field, on the left by the values in a rank-3 container inputData indexed by (C,P,D), representing the values of vector data; the output value container outputFields is indexed by (C,F,P,D,D), regardless of which of the two use cases is considered. More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | outerProductDataData (ArrayOutData &outputData, const ArrayInDataLeft &inputDataLeft, const ArrayInDataRight &inputDataRight) |
| There are two use cases: (1) outer product of a rank-3 container inputDataRight with dimensions (C,P,D), representing the values of a set of vector data, on the left by the values in a rank-3 container inputDataLeft indexed by (C,P,D) representing the values of vector data, OR (2) outer product of a rank-2 container inputDataRight with dimensions (P,D), representing the values of vector data, on the left by the values in a rank-3 container inputDataLeft indexed by (C,P,D), representing the values of vector data; the output value container outputData is indexed by (C,P,D,D), regardless of which of the two use cases is considered. More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | matvecProductDataField (ArrayOutFields &outputFields, const ArrayInData &inputData, const ArrayInFields &inputFields, const char transpose= 'N') |
| There are two use cases: (1) matrix-vector product of a rank-4 container inputFields with dimensions (C,F,P,D), representing the values of a set of vector fields, on the left by the values in a rank-2, 3, or 4 container inputData indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data, OR (2) matrix-vector product of a rank-3 container inputFields with dimensions (F,P,D), representing the values of a vector field, on the left by the values in a rank-2, 3, or 4 container inputData indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data; the output value container outputFields is indexed by (C,F,P,D), regardless of which of the two use cases is considered. More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | matvecProductDataData (ArrayOutData &outputData, const ArrayInDataLeft &inputDataLeft, const ArrayInDataRight &inputDataRight, const char transpose= 'N') |
| There are two use cases: (1) matrix-vector product of a rank-3 container inputDataRight with dimensions (C,P,D), representing the values of a set of vector data, on the left by the values in a rank-2, 3, or 4 container inputDataLeft indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data, OR (2) matrix-vector product of a rank-2 container inputDataRight with dimensions (P,D), representing the values of vector data, on the left by the values in a rank-2, 3, or 4 container inputDataLeft indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data; the output value container outputData is indexed by (C,P,D), regardless of which of the two use cases is considered. More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInData , class ArrayInFields > | |
| static void | matmatProductDataField (ArrayOutFields &outputFields, const ArrayInData &inputData, const ArrayInFields &inputFields, const char transpose= 'N') |
| There are two use cases: (1) matrix-matrix product of a rank-5 container inputFields with dimensions (C,F,P,D1,D2), representing the values of a set of tensor fields, on the left by the values in a rank-2, 3, or 4 container inputData indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data, OR (2) matrix-matrix product of a rank-4 container inputFields with dimensions (F,P,D1,D2), representing the values of a tensor field, on the left by the values in a rank-2, 3, or 4 container inputData indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data; the output value container outputFields is indexed by (C,F,P,D1,D2), regardless of which of the two use cases is considered. More... | |
| template<class Scalar , class ArrayOutData , class ArrayInDataLeft , class ArrayInDataRight > | |
| static void | matmatProductDataData (ArrayOutData &outputData, const ArrayInDataLeft &inputDataLeft, const ArrayInDataRight &inputDataRight, const char transpose= 'N') |
| There are two use cases: (1) matrix-matrix product of a rank-4 container inputDataRight with dimensions (C,P,D1,D2), representing the values of a set of tensor data, on the left by the values in a rank-2, 3, or 4 container inputDataLeft indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data, OR (2) matrix-matrix product of a rank-3 container inputDataRight with dimensions (P,D1,D2), representing the values of tensor data, on the left by the values in a rank-2, 3, or 4 container inputDataLeft indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data; the output value container outputData is indexed by (C,P,D1,D2), regardless of which of the two use cases is considered. More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInFields > | |
| static void | cloneFields (ArrayOutFields &outputFields, const ArrayInFields &inputFields) |
| Replicates a rank-2, 3, or 4 container with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or a tensor field, into an output value container of size (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2). More... | |
| template<class Scalar , class ArrayOutFields , class ArrayInFactors , class ArrayInFields > | |
| static void | cloneScaleFields (ArrayOutFields &outputFields, const ArrayInFactors &inputFactors, const ArrayInFields &inputFields) |
| Multiplies a rank-2, 3, or 4 container with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or a tensor field, F-componentwise with a scalar container indexed by (C,F), and stores the result in an output value container of size (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2). More... | |
| template<class Scalar , class ArrayInOutFields , class ArrayInFactors > | |
| static void | scaleFields (ArrayInOutFields &inoutFields, const ArrayInFactors &inputFactors) |
| Multiplies, in place, a rank-2, 3, or 4 container with dimensions (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2), representing the values of a scalar, vector or a tensor field, F-componentwise with a scalar container indexed by (C,F). More... | |
Detailed Description
Utility class that provides methods for higher-order algebraic manipulation of user-defined arrays, such as tensor contractions. For low-order operations, see Intrepid::RealSpaceTools.
Definition at line 67 of file Intrepid_ArrayTools.hpp.
Member Function Documentation
|
static |
Replicates a rank-2, 3, or 4 container with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or a tensor field, into an output value container of size (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2).
- Parameters
-
outputFields [out] - Output fields array. inputFields [in] - Input fields array.
Definition at line 51 of file Intrepid_ArrayToolsDefCloneScale.hpp.
|
static |
Multiplies a rank-2, 3, or 4 container with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or a tensor field, F-componentwise with a scalar container indexed by (C,F), and stores the result in an output value container of size (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2).
- Parameters
-
outputFields [out] - Output fields array. inputFactors [in] - Input field factors array. inputFields [in] - Input fields array.
Definition at line 136 of file Intrepid_ArrayToolsDefCloneScale.hpp.
|
static |
Contracts the "point" dimensions P of rank-2 containers with dimensions (C,P), and returns the result in a rank-1 container with dimensions (C).
- Parameters
-
outputData [out] - Output data array. inputDataLeft [in] - Left data input array. inputDataRight [in] - Right data input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE.
Definition at line 557 of file Intrepid_ArrayToolsDefContractions.hpp.
|
static |
Contracts the "point" and "space" dimensions P, D1 and D2 of rank-4 containers with dimensions (C,P,D1,D2) and returns the result in a rank-1 container with dimensions (C).
- Parameters
-
outputData [out] - Output data array. inputDataLeft [in] - Left data input array. inputDataRight [in] - Right data input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE.
Definition at line 665 of file Intrepid_ArrayToolsDefContractions.hpp.
|
static |
Contracts the "point" and "space" dimensions P and D of rank-3 containers with dimensions (C,P,D) and returns the result in a rank-1 container with dimensions (C).
- Parameters
-
outputData [out] - Output data array. inputDataLeft [in] - Left data input array. inputDataRight [in] - Right data input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE.
Definition at line 607 of file Intrepid_ArrayToolsDefContractions.hpp.
|
static |
Contracts the "point" dimensions P of a rank-3 containers and a rank-2 container with dimensions (C,F,P) and (C,P), respectively, and returns the result in a rank-2 container with dimensions (C,F).
For a fixed index "C", (C,F) represents a (column) vector of length F.
- Parameters
-
outputFields [out] - Output fields array. inputData [in] - Data array. inputFields [in] - Input fields array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE.
Definition at line 267 of file Intrepid_ArrayToolsDefContractions.hpp.
|
static |
Contracts the "point" and "space" dimensions P, D1 and D2 of a rank-5 container and a rank-4 container with dimensions (C,F,P,D1,D2) and (C,P,D1,D2), respectively, and returns the result in a rank-2 container with dimensions (C,F).
For a fixed index "C", (C,F) represents a (column) vector of length F.
- Parameters
-
outputFields [out] - Output fields array. inputData [in] - Data array. inputFields [in] - Input fields array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE.
Definition at line 450 of file Intrepid_ArrayToolsDefContractions.hpp.
|
static |
Contracts the "point" and "space" dimensions P and D of a rank-4 container and a rank-3 container with dimensions (C,F,P,D) and (C,P,D), respectively, and returns the result in a rank-2 container with dimensions (C,F).
For a fixed index "C", (C,F) represents a (column) vector of length F.
- Parameters
-
outputFields [out] - Output fields array. inputData [in] - Data array. inputFields [in] - Input fields array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE.
Definition at line 354 of file Intrepid_ArrayToolsDefContractions.hpp.
|
static |
Contracts the "point" dimension P of two rank-3 containers with dimensions (C,L,P) and (C,R,P), and returns the result in a rank-3 container with dimensions (C,L,R).
For a fixed index "C", (C,L,R) represents a rectangular L X R matrix where L and R may be different.
- Parameters
-
outputFields [out] - Output array. leftFields [in] - Left input array. rightFields [in] - Right input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE. Contracts the "point" and "space" dimensions P and D1 of two rank-4 containers with dimensions (C,L,P,D1) and (C,R,P,D1), and returns the result in a rank-3 container with dimensions (C,L,R).
For a fixed index "C", (C,L,R) represents a rectangular L X R matrix where L and R may be different.
- Parameters
-
outputFields [out] - Output array. leftFields [in] - Left input array. rightFields [in] - Right input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE. Contracts the "point" and "space" dimensions P, D1, and D2 of two rank-5 containers with dimensions (C,L,P,D1,D2) and (C,R,P,D1,D2), and returns the result in a rank-3 container with dimensions (C,L,R).
For a fixed index "C", (C,L,R) represents a rectangular L X R matrix where L and R may be different.
- Parameters
-
outputFields [out] - Output array. leftFields [in] - Left input array. rightFields [in] - Right input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE. Contracts the "point" dimensions P of a rank-3 containers and a rank-2 container with dimensions (C,F,P) and (C,P), respectively, and returns the result in a rank-2 container with dimensions (C,F).
For a fixed index "C", (C,F) represents a (column) vector of length F.
- Parameters
-
outputFields [out] - Output fields array. inputData [in] - Data array. inputFields [in] - Input fields array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE. Contracts the "point" and "space" dimensions P and D of a rank-4 container and a rank-3 container with dimensions (C,F,P,D) and (C,P,D), respectively, and returns the result in a rank-2 container with dimensions (C,F).
For a fixed index "C", (C,F) represents a (column) vector of length F.
- Parameters
-
outputFields [out] - Output fields array. inputData [in] - Data array. inputFields [in] - Input fields array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE. Contracts the "point" and "space" dimensions P, D1 and D2 of a rank-5 container and a rank-4 container with dimensions (C,F,P,D1,D2) and (C,P,D1,D2), respectively, and returns the result in a rank-2 container with dimensions (C,F).
For a fixed index "C", (C,F) represents a (column) vector of length F.
- Parameters
-
outputFields [out] - Output fields array. inputData [in] - Data array. inputFields [in] - Input fields array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE. Contracts the "point" dimensions P of rank-2 containers with dimensions (C,P), and returns the result in a rank-1 container with dimensions (C).
- Parameters
-
outputData [out] - Output data array. inputDataLeft [in] - Left data input array. inputDataRight [in] - Right data input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE. Contracts the "point" and "space" dimensions P and D of rank-3 containers with dimensions (C,P,D) and returns the result in a rank-1 container with dimensions (C).
- Parameters
-
outputData [out] - Output data array. inputDataLeft [in] - Left data input array. inputDataRight [in] - Right data input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE. Contracts the "point" and "space" dimensions P, D1 and D2 of rank-4 containers with dimensions (C,P,D1,D2) and returns the result in a rank-1 container with dimensions (C).
- Parameters
-
outputData [out] - Output data array. inputDataLeft [in] - Left data input array. inputDataRight [in] - Right data input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE. There are two use cases: (1) multiplies a rank-3, 4, or 5 container inputFields with dimensions (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2), representing the values of a set of scalar, vector or tensor fields, by the values in a rank-2 container inputData indexed by (C,P), representing the values of scalar data, OR (2) multiplies a rank-2, 3, or 4 container inputFields with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or a tensor field, by the values in a rank-2 container inputData indexed by (C,P), representing the values of scalar data; the output value container outputFields is indexed by (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2), regardless of which of the two use cases is considered.
- Note
- The argument inputFields can be changed! This enables in-place multiplication.
- Parameters
-
outputFields [out] - Output (product) fields array. inputData [in] - Data (multiplying) array. inputFields [in] - Input (being multiplied) fields array. reciprocal [in] - If TRUE, divides input fields by the data (instead of multiplying). Default: FALSE.
Definition at line 51 of file Intrepid_ArrayToolsDefContractions.hpp.
|
static |
Contracts the "point" and "space" dimensions P, D1, and D2 of two rank-5 containers with dimensions (C,L,P,D1,D2) and (C,R,P,D1,D2), and returns the result in a rank-3 container with dimensions (C,L,R).
For a fixed index "C", (C,L,R) represents a rectangular L X R matrix where L and R may be different.
- Parameters
-
outputFields [out] - Output array. leftFields [in] - Left input array. rightFields [in] - Right input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE.
Definition at line 189 of file Intrepid_ArrayToolsDefContractions.hpp.
|
static |
Contracts the "point" and "space" dimensions P and D1 of two rank-4 containers with dimensions (C,L,P,D1) and (C,R,P,D1), and returns the result in a rank-3 container with dimensions (C,L,R).
For a fixed index "C", (C,L,R) represents a rectangular L X R matrix where L and R may be different.
- Parameters
-
outputFields [out] - Output array. leftFields [in] - Left input array. rightFields [in] - Right input array. compEngine [in] - Computational engine. sumInto [in] - If TRUE, sum into given output array, otherwise overwrite it. Default: FALSE.
Definition at line 117 of file Intrepid_ArrayToolsDefContractions.hpp.
|
static |
There are two use cases: (1) cross product of a rank-3 container inputDataRight with dimensions (C,P,D), representing the values of a set of vector data, on the left by the values in a rank-3 container inputDataLeft indexed by (C,P,D) representing the values of vector data, OR (2) cross product of a rank-2 container inputDataRight with dimensions (P,D), representing the values of vector data, on the left by the values in a rank-3 container inputDataLeft indexed by (C,P,D), representing the values of vector data; the output value container outputData is indexed by (C,P,D) in 3D (vector output) and by (C,P) in 2D (scalar output), regardless of which of the two use cases is considered.
- Parameters
-
outputData [out] - Output (cross product) data array. inputDataLeft [in] - Left input data array. inputDataRight [in] - Right input data array.
Definition at line 238 of file Intrepid_ArrayToolsDefTensor.hpp.
|
static |
There are two use cases: (1) cross product of a rank-4 container inputFields with dimensions (C,F,P,D), representing the values of a set of vector fields, on the left by the values in a rank-3 container inputData indexed by (C,P,D), representing the values of vector data, OR (2) cross product of a rank-3 container inputFields with dimensions (F,P,D), representing the values of a vector field, on the left by the values in a rank-3 container inputData indexed by (C,P,D), representing the values of vector data; the output value container outputFields is indexed by (C,F,P,D) in 3D (vector output) and by (C,F,P) in 2D (scalar output), regardless of which of the two use cases is considered.
- Parameters
-
outputFields [out] - Output (cross product) fields array. inputData [in] - Data array. inputFields [in] - Input fields array.
Definition at line 55 of file Intrepid_ArrayToolsDefTensor.hpp.
|
static |
There are two use cases: (1) dot product of a rank-2, 3 or 4 container inputDataRight with dimensions (C,P) (C,P,D1) or (C,P,D1,D2), representing the values of a scalar, vector or a tensor set of data, by the values in a rank-2, 3 or 4 container inputDataLeft indexed by (C,P), (C,P,D1), or (C,P,D1,D2) representing the values of scalar, vector or tensor data, OR (2) dot product of a rank-2, 3 or 4 container inputDataRight with dimensions (P), (P,D1) or (P,D1,D2), representing the values of scalar, vector or tensor data, by the values in a rank-2 container inputDataLeft indexed by (C,P), (C,P,D1) or (C,P,D1,D2), representing the values of scalar, vector, or tensor data; the output value container outputData is indexed by (C,P), regardless of which of the two use cases is considered.
For input fields containers without a dimension index, this operation reduces to scalar multiplication.
- Parameters
-
outputData [out] - Output (dot product) data array. inputDataLeft [in] - Left input data array. inputDataRight [in] - Right input data array.
Definition at line 351 of file Intrepid_ArrayToolsDefDot.hpp.
|
static |
There are two use cases: (1) dot product of a rank-3, 4 or 5 container inputFields with dimensions (C,F,P) (C,F,P,D1) or (C,F,P,D1,D2), representing the values of a set of scalar, vector or tensor fields, by the values in a rank-2, 3 or 4 container inputData indexed by (C,P), (C,P,D1), or (C,P,D1,D2) representing the values of scalar, vector or tensor data, OR (2) dot product of a rank-2, 3 or 4 container inputFields with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or tensor field, by the values in a rank-2 container inputData indexed by (C,P), (C,P,D1) or (C,P,D1,D2), representing the values of scalar, vector or tensor data; the output value container outputFields is indexed by (C,F,P), regardless of which of the two use cases is considered.
For input fields containers without a dimension index, this operation reduces to scalar multiplication.
- Parameters
-
outputData [out] - Output (dot product) data array. inputDataRight [in] - Data array Right. inputDataLeft [in] - Data Array Left. invalRank [in] - rank inputDataRight outvalRank [in] - rank output
Definition at line 52 of file Intrepid_ArrayToolsDefDot.hpp.
|
static |
There are two use cases: (1) matrix-matrix product of a rank-4 container inputDataRight with dimensions (C,P,D1,D2), representing the values of a set of tensor data, on the left by the values in a rank-2, 3, or 4 container inputDataLeft indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data, OR (2) matrix-matrix product of a rank-3 container inputDataRight with dimensions (P,D1,D2), representing the values of tensor data, on the left by the values in a rank-2, 3, or 4 container inputDataLeft indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data; the output value container outputData is indexed by (C,P,D1,D2), regardless of which of the two use cases is considered.
- Remarks
- The rank of inputData implicitly defines the type of tensor data:
- rank = 2 corresponds to a constant diagonal tensor
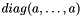
- rank = 3 corresponds to a nonconstant diagonal tensor
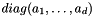
- rank = 4 corresponds to a full tensor
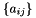
- rank = 2 corresponds to a constant diagonal tensor
- Note
- It is assumed that all tensors are square!
- The method is defined for spatial dimensions D = 1, 2, 3
- Parameters
-
outputData [out] - Output (matrix-vector product) data array. inputDataLeft [in] - Left input data array. inputDataRight [in] - Right input data array. transpose [in] - If 'T', use transposed tensor; if 'N', no transpose. Default: 'N'.
Definition at line 1976 of file Intrepid_ArrayToolsDefTensor.hpp.
|
static |
There are two use cases: (1) matrix-matrix product of a rank-5 container inputFields with dimensions (C,F,P,D1,D2), representing the values of a set of tensor fields, on the left by the values in a rank-2, 3, or 4 container inputData indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data, OR (2) matrix-matrix product of a rank-4 container inputFields with dimensions (F,P,D1,D2), representing the values of a tensor field, on the left by the values in a rank-2, 3, or 4 container inputData indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data; the output value container outputFields is indexed by (C,F,P,D1,D2), regardless of which of the two use cases is considered.
- Remarks
- The rank of inputData implicitly defines the type of tensor data:
- rank = 2 corresponds to a constant diagonal tensor
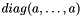
- rank = 3 corresponds to a nonconstant diagonal tensor
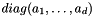
- rank = 4 corresponds to a full tensor
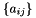
- rank = 2 corresponds to a constant diagonal tensor
- Note
- It is assumed that all tensors are square!
- The method is defined for spatial dimensions D = 1, 2, 3
- Parameters
-
outputFields [out] - Output (matrix-matrix product) fields array. inputData [in] - Data array. inputFields [in] - Input fields array. transpose [in] - If 'T', use transposed tensor; if 'N', no transpose. Default: 'N'.
Definition at line 1497 of file Intrepid_ArrayToolsDefTensor.hpp.
|
static |
There are two use cases: (1) matrix-vector product of a rank-3 container inputDataRight with dimensions (C,P,D), representing the values of a set of vector data, on the left by the values in a rank-2, 3, or 4 container inputDataLeft indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data, OR (2) matrix-vector product of a rank-2 container inputDataRight with dimensions (P,D), representing the values of vector data, on the left by the values in a rank-2, 3, or 4 container inputDataLeft indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data; the output value container outputData is indexed by (C,P,D), regardless of which of the two use cases is considered.
- Remarks
- The rank of inputDataLeft implicitly defines the type of tensor data:
- rank = 2 corresponds to a constant diagonal tensor
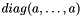
- rank = 3 corresponds to a nonconstant diagonal tensor
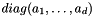
- rank = 4 corresponds to a full tensor
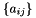
- rank = 2 corresponds to a constant diagonal tensor
- Note
- It is assumed that all tensors are square!
- Parameters
-
outputData [out] - Output (matrix-vector product) data array. inputDataLeft [in] - Left input data array. inputDataRight [in] - Right input data array. transpose [in] - If 'T', use transposed tensor; if 'N', no transpose. Default: 'N'.
Definition at line 1085 of file Intrepid_ArrayToolsDefTensor.hpp.
|
static |
There are two use cases: (1) matrix-vector product of a rank-4 container inputFields with dimensions (C,F,P,D), representing the values of a set of vector fields, on the left by the values in a rank-2, 3, or 4 container inputData indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data, OR (2) matrix-vector product of a rank-3 container inputFields with dimensions (F,P,D), representing the values of a vector field, on the left by the values in a rank-2, 3, or 4 container inputData indexed by (C,P), (C,P,D1) or (C,P,D1,D2), respectively, representing the values of tensor data; the output value container outputFields is indexed by (C,F,P,D), regardless of which of the two use cases is considered.
- Remarks
- The rank of inputData implicitly defines the type of tensor data:
- rank = 2 corresponds to a constant diagonal tensor
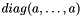
- rank = 3 corresponds to a nonconstant diagonal tensor
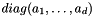
- rank = 4 corresponds to a full tensor
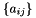
- rank = 2 corresponds to a constant diagonal tensor
- Note
- It is assumed that all tensors are square!
- The method is defined for spatial dimensions D = 1, 2, 3
- Parameters
-
outputFields [out] - Output (matrix-vector product) fields array. inputData [in] - Data array. inputFields [in] - Input fields array. transpose [in] - If 'T', use transposed tensor; if 'N', no transpose. Default: 'N'.
Definition at line 642 of file Intrepid_ArrayToolsDefTensor.hpp.
|
static |
There are two use cases: (1) outer product of a rank-3 container inputDataRight with dimensions (C,P,D), representing the values of a set of vector data, on the left by the values in a rank-3 container inputDataLeft indexed by (C,P,D) representing the values of vector data, OR (2) outer product of a rank-2 container inputDataRight with dimensions (P,D), representing the values of vector data, on the left by the values in a rank-3 container inputDataLeft indexed by (C,P,D), representing the values of vector data; the output value container outputData is indexed by (C,P,D,D), regardless of which of the two use cases is considered.
- Parameters
-
outputData [out] - Output (outer product) data array. inputDataLeft [in] - Left input data array. inputDataRight [in] - Right input data array.
Definition at line 532 of file Intrepid_ArrayToolsDefTensor.hpp.
|
static |
There are two use cases: (1) outer product of a rank-4 container inputFields with dimensions (C,F,P,D), representing the values of a set of vector fields, on the left by the values in a rank-3 container inputData indexed by (C,P,D), representing the values of vector data, OR (2) outer product of a rank-3 container inputFields with dimensions (F,P,D), representing the values of a vector field, on the left by the values in a rank-3 container inputData indexed by (C,P,D), representing the values of vector data; the output value container outputFields is indexed by (C,F,P,D,D), regardless of which of the two use cases is considered.
- Parameters
-
outputFields [out] - Output (outer product) fields array. inputData [in] - Data array. inputFields [in] - Input fields array.
Definition at line 417 of file Intrepid_ArrayToolsDefTensor.hpp.
|
static |
There are two use cases: (1) multiplies a rank-2, 3, or 4 container inputDataRight with dimensions (C,P), (C,P,D1) or (C,P,D1,D2), representing the values of a set of scalar, vector or tensor data, by the values in a rank-2 container inputDataLeft indexed by (C,P), representing the values of scalar data, OR (2) multiplies a rank-1, 2, or 3 container inputDataRight with dimensions (P), (P,D1) or (P,D1,D2), representing the values of scalar, vector or tensor data, by the values in a rank-2 container inputDataLeft indexed by (C,P), representing the values of scalar data; the output value container outputData is indexed by (C,P), (C,P,D1) or (C,P,D1,D2), regardless of which of the two use cases is considered.
- Note
- The arguments inputDataLeft, inputDataRight can be changed! This enables in-place multiplication.
- Parameters
-
outputData [out] - Output data array. inputDataLeft [in] - Left (multiplying) data array. inputDataRight [in] - Right (being multiplied) data array. reciprocal [in] - If TRUE, divides input fields by the data (instead of multiplying). Default: FALSE.
Definition at line 479 of file Intrepid_ArrayToolsDefScalar.hpp.
|
static |
There are two use cases: (1) multiplies a rank-3, 4, or 5 container inputFields with dimensions (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2), representing the values of a set of scalar, vector or tensor fields, by the values in a rank-2 container inputData indexed by (C,P), representing the values of scalar data, OR (2) multiplies a rank-2, 3, or 4 container inputFields with dimensions (F,P), (F,P,D1) or (F,P,D1,D2), representing the values of a scalar, vector or a tensor field, by the values in a rank-2 container inputData indexed by (C,P), representing the values of scalar data; the output value container outputFields is indexed by (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2), regardless of which of the two use cases is considered.
- Note
- The argument inputFields can be changed! This enables in-place multiplication.
- Parameters
-
outputFields [out] - Output (product) fields array. inputData [in] - Data (multiplying) array. inputFields [in] - Input (being multiplied) fields array. reciprocal [in] - If TRUE, divides input fields by the data (instead of multiplying). Default: FALSE.
Definition at line 55 of file Intrepid_ArrayToolsDefScalar.hpp.
|
static |
Multiplies, in place, a rank-2, 3, or 4 container with dimensions (C,F,P), (C,F,P,D1) or (C,F,P,D1,D2), representing the values of a scalar, vector or a tensor field, F-componentwise with a scalar container indexed by (C,F).
- Parameters
-
inoutFields [in/out] - Input / output fields array. inputFactors [in] - Scaling field factors array.
Definition at line 228 of file Intrepid_ArrayToolsDefCloneScale.hpp.
The documentation for this class was generated from the following files:
- http://docs.trilinos.org/r13.0/packages/intrepid/src/Shared/Intrepid_ArrayTools.hpp
- http://docs.trilinos.org/r13.0/packages/intrepid/src/Shared/Intrepid_ArrayToolsDefCloneScale.hpp
- http://docs.trilinos.org/r13.0/packages/intrepid/src/Shared/Intrepid_ArrayToolsDefContractions.hpp
- http://docs.trilinos.org/r13.0/packages/intrepid/src/Shared/Intrepid_ArrayToolsDefDot.hpp
- http://docs.trilinos.org/r13.0/packages/intrepid/src/Shared/Intrepid_ArrayToolsDefScalar.hpp
- http://docs.trilinos.org/r13.0/packages/intrepid/src/Shared/Intrepid_ArrayToolsDefTensor.hpp
 1.8.5
1.8.5