Classes
struct	Cubature
	Gauss-Jacobi/Gauss-Radau-Jacobi/Gauss-Lobatto zeros and weights. More...

struct	Derivative
	Compute the Derivative Matrix and its transpose associated with the Gauss-Jacobi/Gauss-Radau-Jacobi/Gauss-Lobatto-Jacobi zeros. More...

struct	InterpolationOperator
	Interpolation Operator from Gauss-Jacobi points to an arbitrary distribution at points zm. More...

struct	LagrangianInterpolant
	Compute the value of the i th Lagrangian interpolant through the np Gauss-Jacobi/Gauss-Radau-Jacobi/Gauss-Lobatto points zgj at the arbitrary location z. More...

Static Public Member Functions
template<typename zViewType , typename wViewType >
static KOKKOS_INLINE_FUNCTION void	getCubature (zViewType z, wViewType w, const ordinal_type np, const double alpha, const double beta, const EPolyType poly)

template<typename DViewType , typename zViewType >
static KOKKOS_INLINE_FUNCTION void	getDerivative (DViewType D, const zViewType z, const ordinal_type np, const double alpha, const double beta, const EPolyType poly)

template<typename zViewType >
static KOKKOS_INLINE_FUNCTION zViewType::value_type	getLagrangianInterpolant (const ordinal_type i, const typename zViewType::value_type z, const zViewType zgj, const ordinal_type np, const double alpha, const double beta, const EPolyType poly)

template<typename imViewType , typename zgrjViewType , typename zmViewType >
static KOKKOS_INLINE_FUNCTION void	getInterpolationOperator (imViewType im, const zgrjViewType zgrj, const zmViewType zm, const ordinal_type nz, const ordinal_type mz, const double alpha, const double beta, const EPolyType poly)

template<typename zViewType , typename polyiViewType , typename polydViewType >
static KOKKOS_INLINE_FUNCTION void	JacobiPolynomial (const ordinal_type np, const zViewType z, polyiViewType poly_in, polydViewType polyd, const ordinal_type n, const double alpha, const double beta)
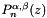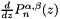	Routine to calculate Jacobi polynomials, $P^{\alpha,\beta}_n(z)$ , and their first derivative, $\frac{d}{dz} P^{\alpha,\beta}_n(z)$ . More...

template<typename zViewType , typename polydViewType >
static KOKKOS_INLINE_FUNCTION void	JacobiPolynomialDerivative (const ordinal_type np, const zViewType z, polydViewType polyd, const ordinal_type n, const double alpha, const double beta)
	Calculate the derivative of Jacobi polynomials. More...

template<typename zViewType , bool DeflationEnabled = false>
static KOKKOS_INLINE_FUNCTION void	JacobiZeros (zViewType z, const ordinal_type n, const double alpha, const double beta)
	Calculate the n zeros, z, of the Jacobi polynomial, i.e. 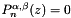$P_n^{\alpha,\beta}(z) = 0$ . More...

template<typename zViewType >
static KOKKOS_INLINE_FUNCTION void	JacobiZerosPolyDeflation (zViewType z, const ordinal_type n, const double alpha, const double beta)

template<typename aViewType >
static KOKKOS_INLINE_FUNCTION void	JacobiZerosTriDiagonal (aViewType a, const ordinal_type n, const double alpha, const double beta)

template<typename aViewType , typename bViewType >
static KOKKOS_INLINE_FUNCTION void	JacobiZeros (aViewType a, bViewType b, const ordinal_type n, const double alpha, const double beta)
	Zero determination through the eigenvalues of a tridiagonal matrix from the three term recursion relationship. More...

template<typename dViewType , typename eViewType >
static KOKKOS_INLINE_FUNCTION void	TriQL (dViewType d, eViewType e, const ordinal_type n)
	QL algorithm for symmetric tridiagonal matrix. More...

static KOKKOS_INLINE_FUNCTION double	GammaFunction (const double x)
	Calculate the Gamma function , 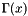$\Gamma(x)$ , for integer values x and halves. More...

Detailed Description

Definition at line 213 of file Intrepid2_Polylib.hpp.

Member Function Documentation

KOKKOS_INLINE_FUNCTION double Intrepid2::Polylib::Serial::GammaFunction ( const double x )

static

Calculate the Gamma function , 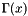$\Gamma(x)$ , for integer values x and halves.

Determine the value of 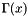$\Gamma(x)$ using:

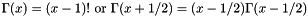
$\Gamma(x) = (x-1)! \mbox{ or } \Gamma(x+1/2) = (x-1/2)\Gamma(x-1/2)$

where 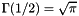$\Gamma(1/2) = \sqrt{\pi}$

Definition at line 877 of file Intrepid2_PolylibDef.hpp.

template<typename zViewType , typename polyiViewType , typename polydViewType >

KOKKOS_INLINE_FUNCTION void Intrepid2::Polylib::Serial::JacobiPolynomial	(	const ordinal_type	np,
		const zViewType	z,
		polyiViewType	poly_in,
		polydViewType	polyd,
		const ordinal_type	n,
		const double	alpha,
		const double	beta
	)

static

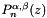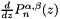Routine to calculate Jacobi polynomials, $P^{\alpha,\beta}_n(z)$ , and their first derivative, $\frac{d}{dz} P^{\alpha,\beta}_n(z)$ .

This function returns the vectors poly_in and poly_d containing the value of the n-th order Jacobi polynomial 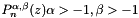$P^{\alpha,\beta}_n(z) \alpha > -1, \beta > -1$ and its derivative at the np points in z[i]

If poly_in = NULL then only calculate derivative
If polyd = NULL then only calculate polynomial
To calculate the polynomial this routine uses the recursion relationship (see appendix A ref [4]) : $\begin{array}{rcl} P^{\alpha,\beta}_0(z) &=& 1 \\ P^{\alpha,\beta}_1(z) &=& \frac{1}{2} [ \alpha-\beta+(\alpha+\beta+2)z] \\ a^1_n P^{\alpha,\beta}_{n+1}(z) &=& (a^2_n + a^3_n z) P^{\alpha,\beta}_n(z) - a^4_n P^{\alpha,\beta}_{n-1}(z) \\ a^1_n &=& 2(n+1)(n+\alpha + \beta + 1)(2n + \alpha + \beta) \\ a^2_n &=& (2n + \alpha + \beta + 1)(\alpha^2 - \beta^2) \\ a^3_n &=& (2n + \alpha + \beta)(2n + \alpha + \beta + 1) (2n + \alpha + \beta + 2) \\ a^4_n &=& 2(n+\alpha)(n+\beta)(2n + \alpha + \beta + 2) \end{array}$
To calculate the derivative of the polynomial this routine uses the relationship (see appendix A ref [4]) : $\begin{array}{rcl} b^1_n(z)\frac{d}{dz} P^{\alpha,\beta}_n(z)&=&b^2_n(z)P^{\alpha,\beta}_n(z) + b^3_n(z) P^{\alpha,\beta}_{n-1}(z) \hspace{2.2cm} \\ b^1_n(z) &=& (2n+\alpha + \beta)(1-z^2) \\ b^2_n(z) &=& n[\alpha - \beta - (2n+\alpha + \beta)z]\\ b^3_n(z) &=& 2(n+\alpha)(n+\beta) \end{array}$
Note the derivative from this routine is only valid for -1 < z < 1.

Definition at line 591 of file Intrepid2_PolylibDef.hpp.

template<typename zViewType , typename polydViewType >

KOKKOS_INLINE_FUNCTION void Intrepid2::Polylib::Serial::JacobiPolynomialDerivative	(	const ordinal_type	np,
		const zViewType	z,
		polydViewType	polyd,
		const ordinal_type	n,
		const double	alpha,
		const double	beta
	)

static

Calculate the derivative of Jacobi polynomials.

Generates a vector poly of values of the derivative of the n-th order Jacobi polynomial 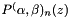$P^(\alpha,\beta)_n(z)$ at the np points z.

To do this we have used the relation
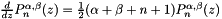
$\frac{d}{dz} P^{\alpha,\beta}_n(z) = \frac{1}{2} (\alpha + \beta + n + 1) P^{\alpha,\beta}_n(z)$

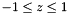
This formulation is valid for $-1 \leq z \leq 1$

Definition at line 678 of file Intrepid2_PolylibDef.hpp.

template<typename zViewType , bool DeflationEnabled>

KOKKOS_INLINE_FUNCTION void Intrepid2::Polylib::Serial::JacobiZeros	(	zViewType	z,
		const ordinal_type	n,
		const double	alpha,
		const double	beta
	)

static

Calculate the n zeros, z, of the Jacobi polynomial, i.e. 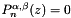$P_n^{\alpha,\beta}(z) = 0$ .

This routine is only valid for 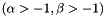$( \alpha > -1, \beta > -1)$ and uses polynomial deflation in a Newton iteration

Definition at line 703 of file Intrepid2_PolylibDef.hpp.

template<typename aViewType , typename bViewType >

static KOKKOS_INLINE_FUNCTION void Intrepid2::Polylib::Serial::JacobiZeros	(	aViewType	a,
		bViewType	b,
		const ordinal_type	n,
		const double	alpha,
		const double	beta
	)

static

Zero determination through the eigenvalues of a tridiagonal matrix from the three term recursion relationship.

Set up a symmetric tridiagonal matrix

$\left [ \begin{array}{ccccc} a[0] & b[0] & & & \\ b[0] & a[1] & b[1] & & \\ 0 & \ddots & \ddots & \ddots & \\ & & \ddots & \ddots & b[n-2] \\ & & & b[n-2] & a[n-1] \end{array} \right ]$

Where the coefficients a[n], b[n] come from the recurrence relation

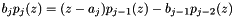
$b_j p_j(z) = (z - a_j ) p_{j-1}(z) - b_{j-1} p_{j-2}(z)$

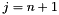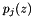where $ j=n+1$ and $p_j(z)$ are the Jacobi (normalized) orthogonal polynomials 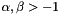$\alpha,\beta > -1$ ( integer values and halves). Since the polynomials are orthonormalized, the tridiagonal matrix is guaranteed to be symmetric. The eigenvalues of this matrix are the zeros of the Jacobi polynomial.

template<typename dViewType , typename eViewType >

KOKKOS_INLINE_FUNCTION void Intrepid2::Polylib::Serial::TriQL	(	dViewType	d,
		eViewType	e,
		const ordinal_type	n
	)

static

QL algorithm for symmetric tridiagonal matrix.

This subroutine is a translation of an algol procedure, num. math. 12, 377-383(1968) by martin and wilkinson, as modified in num. math. 15, 450(1970) by dubrulle. Handbook for auto. comp., vol.ii-linear algebra, 241-248(1971). This is a modified version from numerical recipes.

This subroutine finds the eigenvalues and first components of the eigenvectors of a symmetric tridiagonal matrix by the implicit QL method.

on input:

n is the order of the matrix;
d contains the diagonal elements of the input matrix;
e contains the subdiagonal elements of the input matrix in its first n-1 positions. e(n) is arbitrary;

on output:

d contains the eigenvalues in ascending order.
e has been destroyed;

Definition at line 807 of file Intrepid2_PolylibDef.hpp.

The documentation for this struct was generated from the following files:

http://docs.trilinos.org/r13.0/packages/intrepid2/src/Shared/Intrepid2_Polylib.hpp
http://docs.trilinos.org/r13.0/packages/intrepid2/src/Shared/Intrepid2_PolylibDef.hpp

Classes

Static Public Member Functions

Detailed Description

Member Function Documentation