|
Tpetra parallel linear algebra
Version of the Day
|
All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Pages
|
Tpetra parallel linear algebra
Version of the Day
|
Partial specialization of CrsMatrix for the new Kokkos wrapper Nodes. More...
#include <Tpetra_KokkosRefactor_CrsMatrix_decl.hpp>
Public Types | |
Typedefs | |
| typedef Scalar | scalar_type |
| This class' first template parameter; the type of each entry in the matrix. More... | |
| typedef Kokkos::Details::ArithTraits < Scalar >::val_type | impl_scalar_type |
The type used internally in place of Scalar. More... | |
| typedef LocalOrdinal | local_ordinal_type |
| This class' second template parameter; the type of local indices. More... | |
| typedef GlobalOrdinal | global_ordinal_type |
| This class' third template parameter; the type of global indices. More... | |
| typedef DeviceType | execution_space |
| This class' fourth template parameter; the Kokkos device type. More... | |
| typedef Kokkos::Details::ArithTraits < impl_scalar_type >::mag_type | mag_type |
| Type of a norm result. More... | |
| typedef Kokkos::Compat::KokkosDeviceWrapperNode < DeviceType > | node_type |
| The Kokkos Node type used by this class. More... | |
| typedef Map< LocalOrdinal, GlobalOrdinal, node_type > | map_type |
| The Map specialization suitable for this CrsMatrix specialization. More... | |
| typedef Import< LocalOrdinal, GlobalOrdinal, node_type > | import_type |
| The Import specialization suitable for this CrsMatrix specialization. More... | |
| typedef Export< LocalOrdinal, GlobalOrdinal, node_type > | export_type |
| The Export specialization suitable for this CrsMatrix specialization. More... | |
| typedef CrsGraph< LocalOrdinal, GlobalOrdinal, node_type > | crs_graph_type |
| The CrsGraph specialization suitable for this CrsMatrix specialization. More... | |
| typedef crs_graph_type::local_graph_type | local_graph_type |
| The part of the sparse matrix's graph on each MPI process. More... | |
| typedef Kokkos::CrsMatrix < impl_scalar_type, LocalOrdinal, execution_space, void, typename local_graph_type::size_type > | local_matrix_type |
| The specialization of Kokkos::CrsMatrix that represents the part of the sparse matrix on each MPI process. More... | |
| typedef local_matrix_type::row_map_type t_RowPtrs | TPETRA_DEPRECATED |
DEPRECATED; use local_matrix_type::row_map_type instead. More... | |
| typedef local_matrix_type::row_map_type::non_const_type t_RowPtrsNC | TPETRA_DEPRECATED |
DEPRECATED; use local_matrix_type::row_map_type::non_const_type instead. More... | |
| typedef local_graph_type::entries_type::non_const_type t_LocalOrdinal_1D | TPETRA_DEPRECATED |
DEPRECATED; use local_graph_type::entries_type::non_const_type instead. More... | |
| typedef local_matrix_type::values_type t_ValuesType | TPETRA_DEPRECATED |
DEPRECATED; use local_matrix_type::values_type instead. More... | |
| typedef local_matrix_type k_local_matrix_type | TPETRA_DEPRECATED |
| DEPRECATED; use local_matrix_type instead. More... | |
Public Member Functions | |
| local_matrix_type::values_type | getLocalValuesView () const |
| Get the Kokkos local values. More... | |
| void | importAndFillComplete (Teuchos::RCP< CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, node_type > > &destMatrix, const import_type &importer, const Teuchos::RCP< const map_type > &domainMap, const Teuchos::RCP< const map_type > &rangeMap, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) const |
Import from this to the given destination matrix, and make the result fill complete. More... | |
| void | exportAndFillComplete (Teuchos::RCP< CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, node_type > > &destMatrix, const export_type &exporter, const Teuchos::RCP< const map_type > &domainMap=Teuchos::null, const Teuchos::RCP< const map_type > &rangeMap=Teuchos::null, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) const |
Export from this to the given destination matrix, and make the result fill complete. More... | |
Methods for inserting, modifying, or removing entries | |
| void | insertGlobalValues (const GlobalOrdinal globalRow, const Teuchos::ArrayView< const GlobalOrdinal > &cols, const Teuchos::ArrayView< const Scalar > &vals) |
| Insert one or more entries into the matrix, using global indices. More... | |
| void | insertLocalValues (const LocalOrdinal localRow, const ArrayView< const LocalOrdinal > &cols, const ArrayView< const Scalar > &vals) |
| Insert one or more entries into the matrix, using local indices. More... | |
| LocalOrdinal | replaceGlobalValues (GlobalOrdinal globalRow, const ArrayView< const GlobalOrdinal > &cols, const ArrayView< const Scalar > &vals) |
| Replace one or more entries' values, using global indices. More... | |
| LocalOrdinal | replaceLocalValues (const LocalOrdinal localRow, const ArrayView< const LocalOrdinal > &cols, const ArrayView< const Scalar > &vals) |
| Replace one or more entries' values, using local indices. More... | |
| LocalOrdinal | sumIntoGlobalValues (const GlobalOrdinal globalRow, const ArrayView< const GlobalOrdinal > &cols, const ArrayView< const Scalar > &vals) |
| Sum into one or more sparse matrix entries, using global indices. More... | |
| LocalOrdinal | sumIntoLocalValues (const LocalOrdinal localRow, const ArrayView< const LocalOrdinal > &cols, const ArrayView< const Scalar > &vals) |
| Sum into one or more sparse matrix entries, using local indices. More... | |
| void | setAllToScalar (const Scalar &alpha) |
Set all matrix entries equal to alpha. More... | |
| void | scale (const Scalar &alpha) |
Scale the matrix's values: this := alpha*this. More... | |
| void | setAllValues (const typename local_matrix_type::row_map_type &rowPointers, const typename local_graph_type::entries_type::non_const_type &columnIndices, const typename local_matrix_type::values_type &values) |
| Sets the 1D pointer arrays of the graph. More... | |
| void | setAllValues (const Teuchos::ArrayRCP< size_t > &rowPointers, const Teuchos::ArrayRCP< LocalOrdinal > &columnIndices, const Teuchos::ArrayRCP< Scalar > &values) |
| Sets the 1D pointer arrays of the graph. More... | |
| void | getAllValues (Teuchos::ArrayRCP< const size_t > &rowPointers, Teuchos::ArrayRCP< const LocalOrdinal > &columnIndices, Teuchos::ArrayRCP< const Scalar > &values) const |
Transformational methods | |
| void | globalAssemble () |
| Communicate nonlocal contributions to other processes. More... | |
| void | resumeFill (const RCP< ParameterList > ¶ms=null) |
| Resume operations that may change the values or structure of the matrix. More... | |
| void | fillComplete (const RCP< const map_type > &domainMap, const RCP< const map_type > &rangeMap, const RCP< ParameterList > ¶ms=null) |
| Signal that data entry is complete, specifying domain and range maps. More... | |
| void | fillComplete (const RCP< ParameterList > ¶ms=null) |
| Signal that data entry is complete. More... | |
| void | expertStaticFillComplete (const RCP< const map_type > &domainMap, const RCP< const map_type > &rangeMap, const RCP< const import_type > &importer=Teuchos::null, const RCP< const export_type > &exporter=Teuchos::null, const RCP< ParameterList > ¶ms=Teuchos::null) |
| Perform a fillComplete on a matrix that already has data. More... | |
| void | replaceColMap (const Teuchos::RCP< const map_type > &newColMap) |
| Replace the matrix's column Map with the given Map. More... | |
| void | reindexColumns (crs_graph_type *const graph, const Teuchos::RCP< const map_type > &newColMap, const Teuchos::RCP< const import_type > &newImport=Teuchos::null, const bool sortEachRow=true) |
| Reindex the column indices in place, and replace the column Map. Optionally, replace the Import object as well. More... | |
| void | replaceDomainMapAndImporter (const Teuchos::RCP< const map_type > &newDomainMap, Teuchos::RCP< const import_type > &newImporter) |
| Replace the current domain Map and Import with the given objects. More... | |
| virtual void | removeEmptyProcessesInPlace (const Teuchos::RCP< const map_type > &newMap) |
| Remove processes owning zero rows from the Maps and their communicator. More... | |
Methods implementing RowMatrix | |
| Teuchos::RCP< const Teuchos::Comm< int > > | getComm () const |
| The communicator over which the matrix is distributed. More... | |
| Teuchos::RCP< node_type > | getNode () const |
| The Kokkos Node instance. More... | |
| Teuchos::RCP< const map_type > | getRowMap () const |
| The Map that describes the row distribution in this matrix. More... | |
| Teuchos::RCP< const map_type > | getColMap () const |
| The Map that describes the column distribution in this matrix. More... | |
| Teuchos::RCP< const RowGraph < LocalOrdinal, GlobalOrdinal, node_type > > | getGraph () const |
| This matrix's graph, as a RowGraph. More... | |
| Teuchos::RCP< const crs_graph_type > | getCrsGraph () const |
| This matrix's graph, as a CrsGraph. More... | |
| local_matrix_type | getLocalMatrix () const |
| The local sparse matrix. More... | |
| global_size_t | getGlobalNumRows () const |
| Number of global elements in the row map of this matrix. More... | |
| global_size_t | getGlobalNumCols () const |
| The number of global columns in the matrix. More... | |
| size_t | getNodeNumRows () const |
| The number of matrix rows owned by the calling process. More... | |
| size_t | getNodeNumCols () const |
| The number of columns connected to the locally owned rows of this matrix. More... | |
| GlobalOrdinal | getIndexBase () const |
| The index base for global indices for this matrix. More... | |
| global_size_t | getGlobalNumEntries () const |
| The global number of entries in this matrix. More... | |
| size_t | getNodeNumEntries () const |
| The local number of entries in this matrix. More... | |
| size_t | getNumEntriesInGlobalRow (GlobalOrdinal globalRow) const |
| Returns the current number of entries on this node in the specified global row. More... | |
| size_t | getNumEntriesInLocalRow (LocalOrdinal localRow) const |
| Returns the current number of entries on this node in the specified local row. More... | |
| global_size_t | getGlobalNumDiags () const |
| Returns the number of global diagonal entries, based on global row/column index comparisons. More... | |
| size_t | getNodeNumDiags () const |
| Returns the number of local diagonal entries, based on global row/column index comparisons. More... | |
| size_t | getGlobalMaxNumRowEntries () const |
| Returns the maximum number of entries across all rows/columns on all nodes. More... | |
| size_t | getNodeMaxNumRowEntries () const |
| Returns the maximum number of entries across all rows/columns on this node. More... | |
| bool | hasColMap () const |
| Indicates whether the matrix has a well-defined column map. More... | |
| bool | isLowerTriangular () const |
| Indicates whether the matrix is lower triangular. More... | |
| bool | isUpperTriangular () const |
| Indicates whether the matrix is upper triangular. More... | |
| bool | isLocallyIndexed () const |
| Whether the matrix is locally indexed on the calling process. More... | |
| bool | isGloballyIndexed () const |
| Whether the matrix is globally indexed on the calling process. More... | |
| bool | isFillComplete () const |
| Whether the matrix is fill complete. More... | |
| bool | isFillActive () const |
| Whether the matrix is not fill complete. More... | |
| bool | isStorageOptimized () const |
Returns true if storage has been optimized. More... | |
| ProfileType | getProfileType () const |
Returns true if the matrix was allocated with static data structures. More... | |
| bool | isStaticGraph () const |
| Indicates that the graph is static, so that new entries cannot be added to this matrix. More... | |
| mag_type | getFrobeniusNorm () const |
| Compute and return the Frobenius norm of the matrix. More... | |
| virtual bool | supportsRowViews () const |
Return true if getLocalRowView() and getGlobalRowView() are valid for this object. More... | |
| void | getGlobalRowCopy (GlobalOrdinal GlobalRow, const Teuchos::ArrayView< GlobalOrdinal > &Indices, const Teuchos::ArrayView< Scalar > &Values, size_t &NumEntries) const |
| Fill given arrays with a deep copy of the locally owned entries of the matrix in a given row, using global column indices. More... | |
| void | getLocalRowCopy (LocalOrdinal localRow, const Teuchos::ArrayView< LocalOrdinal > &colInds, const Teuchos::ArrayView< Scalar > &vals, size_t &numEntries) const |
| Fill given arrays with a deep copy of the locally owned entries of the matrix in a given row, using local column indices. More... | |
| void | getGlobalRowView (GlobalOrdinal GlobalRow, Teuchos::ArrayView< const GlobalOrdinal > &indices, Teuchos::ArrayView< const Scalar > &values) const |
| Get a constant, nonpersisting view of a row of this matrix, using global row and column indices. More... | |
| void | getLocalRowView (LocalOrdinal LocalRow, Teuchos::ArrayView< const LocalOrdinal > &indices, Teuchos::ArrayView< const Scalar > &values) const |
| Get a constant, nonpersisting view of a row of this matrix, using local row and column indices. More... | |
| void | getLocalDiagCopy (Vector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &diag) const |
| Get a copy of the diagonal entries of the matrix. More... | |
| void | getLocalDiagOffsets (Teuchos::ArrayRCP< size_t > &offsets) const |
| Get offsets of the diagonal entries in the matrix. More... | |
| void | getLocalDiagCopy (Vector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &diag, const Teuchos::ArrayView< const size_t > &offsets) const |
| Variant of getLocalDiagCopy() that uses precomputed offsets. More... | |
| void | leftScale (const Vector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &x) |
| void | rightScale (const Vector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &x) |
Advanced templated methods | |
| template<class DomainScalar , class RangeScalar > | |
| void | localMultiply (const MultiVector< DomainScalar, LocalOrdinal, GlobalOrdinal, node_type > &X, MultiVector< RangeScalar, LocalOrdinal, GlobalOrdinal, node_type > &Y, Teuchos::ETransp mode, RangeScalar alpha, RangeScalar beta) const |
| Compute a sparse matrix-MultiVector product local to each process. More... | |
| template<class DomainScalar , class RangeScalar > | |
| void | localGaussSeidel (const MultiVector< DomainScalar, LocalOrdinal, GlobalOrdinal, node_type > &B, MultiVector< RangeScalar, LocalOrdinal, GlobalOrdinal, node_type > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &D, const RangeScalar &dampingFactor, const KokkosClassic::ESweepDirection direction) const |
Gauss-Seidel or SOR on  . More... | |
| template<class DomainScalar , class RangeScalar > | |
| void | reorderedLocalGaussSeidel (const MultiVector< DomainScalar, LocalOrdinal, GlobalOrdinal, node_type > &B, MultiVector< RangeScalar, LocalOrdinal, GlobalOrdinal, node_type > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &D, const Teuchos::ArrayView< LocalOrdinal > &rowIndices, const RangeScalar &dampingFactor, const KokkosClassic::ESweepDirection direction) const |
| Reordered Gauss-Seidel or SOR on . More... | |
| template<class DomainScalar , class RangeScalar > | |
| void | localSolve (const MultiVector< RangeScalar, LocalOrdinal, GlobalOrdinal, node_type > &Y, MultiVector< DomainScalar, LocalOrdinal, GlobalOrdinal, node_type > &X, Teuchos::ETransp mode) const |
| Solves a linear system when the underlying matrix is locally triangular. More... | |
| template<class T > | |
| Teuchos::RCP< CrsMatrix< T, LocalOrdinal, GlobalOrdinal, node_type > > | convert () const |
Return another CrsMatrix with the same entries, but converted to a different Scalar type T. More... | |
Methods implementing Operator | |
| void | apply (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &X, MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &Y, Teuchos::ETransp mode=Teuchos::NO_TRANS, Scalar alpha=ScalarTraits< Scalar >::one(), Scalar beta=ScalarTraits< Scalar >::zero()) const |
| Compute a sparse matrix-MultiVector multiply. More... | |
| bool | hasTransposeApply () const |
| Whether apply() allows applying the transpose or conjugate transpose. More... | |
| Teuchos::RCP< const map_type > | getDomainMap () const |
| The domain Map of this matrix. More... | |
| Teuchos::RCP< const map_type > | getRangeMap () const |
| The range Map of this matrix. More... | |
Other "apply"-like methods | |
| void | gaussSeidel (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &B, MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &D, const Scalar &dampingFactor, const ESweepDirection direction, const int numSweeps) const |
| "Hybrid" Jacobi + (Gauss-Seidel or SOR) on . More... | |
| void | reorderedGaussSeidel (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &B, MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &D, const Teuchos::ArrayView< LocalOrdinal > &rowIndices, const Scalar &dampingFactor, const ESweepDirection direction, const int numSweeps) const |
| Reordered "Hybrid" Jacobi + (Gauss-Seidel or SOR) on . More... | |
| void | gaussSeidelCopy (MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &B, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &D, const Scalar &dampingFactor, const ESweepDirection direction, const int numSweeps, const bool zeroInitialGuess) const |
| Version of gaussSeidel(), with fewer requirements on X. More... | |
| void | reorderedGaussSeidelCopy (MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &B, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &D, const Teuchos::ArrayView< LocalOrdinal > &rowIndices, const Scalar &dampingFactor, const ESweepDirection direction, const int numSweeps, const bool zeroInitialGuess) const |
| Version of reorderedGaussSeidel(), with fewer requirements on X. More... | |
| virtual Teuchos::RCP < RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, node_type > > | add (const Scalar &alpha, const RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, node_type > &A, const Scalar &beta, const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, node_type > > &domainMap, const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, node_type > > &rangeMap, const Teuchos::RCP< Teuchos::ParameterList > ¶ms) const |
Implementation of RowMatrix::add: return alpha*A + beta*this. More... | |
Implementation of Teuchos::Describable interface | |
| std::string | description () const |
| A one-line description of this object. More... | |
| void | describe (Teuchos::FancyOStream &out, const Teuchos::EVerbosityLevel verbLevel=Teuchos::Describable::verbLevel_default) const |
| Print the object with some verbosity level to an FancyOStream object. More... | |
Extraction Methods | |
| virtual void | getGlobalRowView (GlobalOrdinal GlobalRow, ArrayView< const GlobalOrdinal > &indices, ArrayView< const Scalar > &values) const =0 |
| Get a constant, nonpersisting, globally indexed view of the given row of the matrix. More... | |
| virtual void | getLocalRowView (LocalOrdinal LocalRow, ArrayView< const LocalOrdinal > &indices, ArrayView< const Scalar > &values) const =0 |
| Get a constant, nonpersisting, locally indexed view of the given row of the matrix. More... | |
| virtual void | getLocalDiagCopy (Vector< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >::classic > &diag) const =0 |
| Get a copy of the diagonal entries, distributed by the row Map. More... | |
Mathematical methods | |
| virtual void | leftScale (const Vector< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >::classic > &x)=0 |
| Scale the RowMatrix on the left with the given Vector x. More... | |
| virtual void | rightScale (const Vector< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >::classic > &x)=0 |
| Scale the RowMatrix on the right with the given Vector x. More... | |
Protected Member Functions | |
| void | allocateValues (ELocalGlobal lg, GraphAllocationStatus gas) |
| Allocate values (and optionally indices) using the Node. More... | |
| void | sortEntries () |
| Sort the entries of each row by their column indices. More... | |
| void | mergeRedundantEntries () |
| Merge entries in each row with the same column indices. More... | |
| void | clearGlobalConstants () |
| Clear matrix properties that require collectives. More... | |
| void | computeGlobalConstants () |
| Compute matrix properties that require collectives. More... | |
| Teuchos::RCP< MV > | getColumnMapMultiVector (const MV &X_domainMap, const bool force=false) const |
| Create a (or fetch a cached) column Map MultiVector. More... | |
| Teuchos::RCP< MV > | getRowMapMultiVector (const MV &Y_rangeMap, const bool force=false) const |
| Create a (or fetch a cached) row Map MultiVector. More... | |
| void | applyNonTranspose (const MV &X_in, MV &Y_in, Scalar alpha, Scalar beta) const |
Special case of apply() for mode == Teuchos::NO_TRANS. More... | |
| void | applyTranspose (const MV &X_in, MV &Y_in, const Teuchos::ETransp mode, Scalar alpha, Scalar beta) const |
Special case of apply() for mode != Teuchos::NO_TRANS. More... | |
| Teuchos::ArrayView< const impl_scalar_type > | getView (RowInfo rowinfo) const |
| Constant view of all entries (including extra space) in the given row. More... | |
| Teuchos::ArrayView < impl_scalar_type > | getViewNonConst (RowInfo rowinfo) |
| Nonconst view of all entries (including extra space) in the given row. More... | |
| void | fillLocalMatrix (const Teuchos::RCP< Teuchos::ParameterList > ¶ms) |
| Fill data into the local matrix. More... | |
| void | fillLocalGraphAndMatrix (const Teuchos::RCP< Teuchos::ParameterList > ¶ms) |
| Fill data into the local graph and matrix. More... | |
| void | checkInternalState () const |
| Check that this object's state is sane; throw if it's not. More... | |
Protected Attributes | |
| Teuchos::RCP< MV > | importMV_ |
| Column Map MultiVector used in apply() and gaussSeidel(). More... | |
| Teuchos::RCP< MV > | exportMV_ |
| Row Map MultiVector used in apply(). More... | |
| local_matrix_type | lclMatrix_ |
| The local sparse matrix. More... | |
| Details::EStorageStatus | storageStatus_ |
| Status of the matrix's storage, when not in a fill-complete state. More... | |
| bool | fillComplete_ |
| Whether the matrix is fill complete. More... | |
| std::map< GlobalOrdinal, std::pair< Teuchos::Array < GlobalOrdinal > , Teuchos::Array< Scalar > > > | nonlocals_ |
| Nonlocal data added using insertGlobalValues(). More... | |
| mag_type | frobNorm_ |
| Cached Frobenius norm of the (global) matrix. More... | |
(Global) graph pointers | |
We keep two graph pointers in order to maintain const correctness. myGraph_ is a graph which we create internally. Operations that change the sparsity structure also modify myGraph_. If myGraph_ != null, then staticGraph_ == myGraph_ pointerwise (we set the pointers equal to each other when we create myGraph_). myGraph_ is only null if this CrsMatrix was created using the constructor with a const CrsGraph input argument. In this case, staticGraph_ is set to the input CrsGraph. | |
| Teuchos::RCP< const Graph > | staticGraph_ |
| Teuchos::RCP< Graph > | myGraph_ |
Sparse matrix values. | |
k_values1D_ represents the values assuming "1-D" compressed sparse row storage. values2D_ represents the values as an array of arrays, one (inner) array per row of the sparse matrix. Before allocation, both arrays are null. After allocation, one is null. If static allocation, then values2D_ is null. If dynamic allocation, then k_values1D_ is null. The allocation always matches that of graph_, as the graph does the allocation for the matrix. | |
| local_matrix_type::values_type | k_values1D_ |
|
Teuchos::ArrayRCP < Teuchos::Array < impl_scalar_type > > | values2D_ |
Constructors and destructor | |
| template<class S2 , class LO2 , class GO2 , class N2 , const bool isClassic> | |
| class | CrsMatrix |
| CrsMatrix (const Teuchos::RCP< const map_type > &rowMap, size_t maxNumEntriesPerRow, ProfileType pftype=DynamicProfile, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) | |
| Constructor specifying fixed number of entries for each row. More... | |
| CrsMatrix (const Teuchos::RCP< const map_type > &rowMap, const Teuchos::ArrayRCP< const size_t > &NumEntriesPerRowToAlloc, ProfileType pftype=DynamicProfile, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) | |
| Constructor specifying (possibly different) number of entries in each row. More... | |
| CrsMatrix (const Teuchos::RCP< const map_type > &rowMap, const Teuchos::RCP< const map_type > &colMap, size_t maxNumEntriesPerRow, ProfileType pftype=DynamicProfile, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) | |
| Constructor specifying column Map and fixed number of entries for each row. More... | |
| CrsMatrix (const Teuchos::RCP< const map_type > &rowMap, const Teuchos::RCP< const map_type > &colMap, const Teuchos::ArrayRCP< const size_t > &NumEntriesPerRowToAlloc, ProfileType pftype=DynamicProfile, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) | |
| Constructor specifying column Map and number of entries in each row. More... | |
| CrsMatrix (const Teuchos::RCP< const crs_graph_type > &graph, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=Teuchos::null) | |
| Constructor specifying a previously constructed graph. More... | |
| CrsMatrix (const Teuchos::RCP< const map_type > &rowMap, const Teuchos::RCP< const map_type > &colMap, const typename local_matrix_type::row_map_type &rowPointers, const typename local_graph_type::entries_type::non_const_type &columnIndices, const typename local_matrix_type::values_type &values, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=null) | |
| Constructor specifying column Map and arrays containing the matrix in sorted local indices. More... | |
| CrsMatrix (const Teuchos::RCP< const map_type > &rowMap, const Teuchos::RCP< const map_type > &colMap, const Teuchos::ArrayRCP< size_t > &rowPointers, const Teuchos::ArrayRCP< LocalOrdinal > &columnIndices, const Teuchos::ArrayRCP< Scalar > &values, const Teuchos::RCP< ParameterList > ¶ms=null) | |
| Constructor specifying column Map and arrays containing the matrix in sorted, local ids. More... | |
| CrsMatrix (const Teuchos::RCP< const map_type > &rowMap, const Teuchos::RCP< const map_type > &colMap, const local_matrix_type &lclMatrix, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=null) | |
| Constructor specifying column Map and a local matrix, which the resulting CrsMatrix views. More... | |
| template<class Node2 > | |
| Teuchos::RCP< CrsMatrix < Scalar, LocalOrdinal, GlobalOrdinal, Node2 > > | clone (const Teuchos::RCP< Node2 > &node2, const Teuchos::RCP< Teuchos::ParameterList > ¶ms=null) const |
| Create a deep copy of this CrsMatrix, where the copy may have a different Node type. More... | |
| virtual | ~CrsMatrix () |
| Destructor. More... | |
Implementation of DistObject interface | |
| virtual bool | checkSizes (const SrcDistObject &source) |
| virtual void | copyAndPermute (const SrcDistObject &source, size_t numSameIDs, const Teuchos::ArrayView< const LocalOrdinal > &permuteToLIDs, const Teuchos::ArrayView< const LocalOrdinal > &permuteFromLIDs) |
| virtual void | packAndPrepare (const SrcDistObject &source, const Teuchos::ArrayView< const LocalOrdinal > &exportLIDs, Teuchos::Array< char > &exports, const Teuchos::ArrayView< size_t > &numPacketsPerLID, size_t &constantNumPackets, Distributor &distor) |
| void | unpackAndCombine (const Teuchos::ArrayView< const LocalOrdinal > &importLIDs, const Teuchos::ArrayView< const char > &imports, const Teuchos::ArrayView< size_t > &numPacketsPerLID, size_t constantNumPackets, Distributor &distor, CombineMode combineMode) |
| Unpack the imported column indices and values, and combine into matrix. More... | |
Implementation of Packable interface | |
| virtual void | pack (const Teuchos::ArrayView< const LocalOrdinal > &exportLIDs, Teuchos::Array< char > &exports, const Teuchos::ArrayView< size_t > &numPacketsPerLID, size_t &constantNumPackets, Distributor &distor) const |
| Pack this object's data for an Import or Export. More... | |
Partial specialization of CrsMatrix for the new Kokkos wrapper Nodes.
This implements the "Kokkos refactor" version of CrsMatrix. For full documentation, see the "classic" version of CrsMatrix.
Definition at line 71 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef Scalar Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::scalar_type |
This class' first template parameter; the type of each entry in the matrix.
Definition at line 91 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef Kokkos::Details::ArithTraits<Scalar>::val_type Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::impl_scalar_type |
The type used internally in place of Scalar.
Some Scalar types might not work with Kokkos on all execution spaces, due to missing CUDA device macros or volatile overloads. The C++ standard type std::complex<T> has this problem. To fix this, we replace std::complex<T> values internally with the (usually) bitwise identical type Kokkos::complex<T>. The latter is the impl_scalar_type corresponding to Scalar = std::complex.
Definition at line 101 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef LocalOrdinal Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::local_ordinal_type |
This class' second template parameter; the type of local indices.
Definition at line 103 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef GlobalOrdinal Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::global_ordinal_type |
This class' third template parameter; the type of global indices.
Definition at line 105 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef DeviceType Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::execution_space |
This class' fourth template parameter; the Kokkos device type.
Definition at line 107 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef Kokkos::Details::ArithTraits<impl_scalar_type>::mag_type Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::mag_type |
Type of a norm result.
This is usually the same as the type of the magnitude (absolute value) of Scalar, but may differ for certain Scalar types.
Definition at line 114 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef Kokkos::Compat::KokkosDeviceWrapperNode<DeviceType> Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::node_type |
The Kokkos Node type used by this class.
This type depends on the DeviceType template parameter. In this, the Kokkos refactor version of Tpetra, it exists only for backwards compatibility.
Definition at line 121 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef Map<LocalOrdinal, GlobalOrdinal, node_type> Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::map_type |
The Map specialization suitable for this CrsMatrix specialization.
Definition at line 124 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef Import<LocalOrdinal, GlobalOrdinal, node_type> Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::import_type |
The Import specialization suitable for this CrsMatrix specialization.
Definition at line 127 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef Export<LocalOrdinal, GlobalOrdinal, node_type> Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::export_type |
The Export specialization suitable for this CrsMatrix specialization.
Definition at line 130 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef CrsGraph<LocalOrdinal, GlobalOrdinal, node_type> Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::crs_graph_type |
The CrsGraph specialization suitable for this CrsMatrix specialization.
Definition at line 133 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef crs_graph_type::local_graph_type Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::local_graph_type |
The part of the sparse matrix's graph on each MPI process.
Definition at line 136 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef Kokkos::CrsMatrix<impl_scalar_type, LocalOrdinal, execution_space,void, typename local_graph_type::size_type> Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::local_matrix_type |
The specialization of Kokkos::CrsMatrix that represents the part of the sparse matrix on each MPI process.
Definition at line 141 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef local_matrix_type::row_map_type t_RowPtrs Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::TPETRA_DEPRECATED |
DEPRECATED; use local_matrix_type::row_map_type instead.
Definition at line 144 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef local_matrix_type::row_map_type::non_const_type t_RowPtrsNC Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::TPETRA_DEPRECATED |
DEPRECATED; use local_matrix_type::row_map_type::non_const_type instead.
Definition at line 146 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef local_graph_type::entries_type::non_const_type t_LocalOrdinal_1D Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::TPETRA_DEPRECATED |
DEPRECATED; use local_graph_type::entries_type::non_const_type instead.
Definition at line 148 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef local_matrix_type::values_type t_ValuesType Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::TPETRA_DEPRECATED |
DEPRECATED; use local_matrix_type::values_type instead.
Definition at line 150 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| typedef local_matrix_type k_local_matrix_type Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::TPETRA_DEPRECATED |
DEPRECATED; use local_matrix_type instead.
Definition at line 153 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::CrsMatrix | ( | const Teuchos::RCP< const map_type > & | rowMap, |
| size_t | maxNumEntriesPerRow, | ||
| ProfileType | pftype = DynamicProfile, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Constructor specifying fixed number of entries for each row.
| rowMap | [in] Distribution of rows of the matrix. |
| maxNumEntriesPerRow | [in] Maximum number of matrix entries per row. If pftype==DynamicProfile, this is only a hint, and you can set this to zero without affecting correctness. If pftype==StaticProfile, this sets the amount of storage allocated, and you cannot exceed this number of entries in any row. |
| pftype | [in] Whether to allocate storage dynamically (DynamicProfile) or statically (StaticProfile). |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::CrsMatrix | ( | const Teuchos::RCP< const map_type > & | rowMap, |
| const Teuchos::ArrayRCP< const size_t > & | NumEntriesPerRowToAlloc, | ||
| ProfileType | pftype = DynamicProfile, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Constructor specifying (possibly different) number of entries in each row.
| rowMap | [in] Distribution of rows of the matrix. |
| NumEntriesPerRowToAlloc | [in] Maximum number of matrix entries to allocate for each row. If pftype==DynamicProfile, this is only a hint. If pftype==StaticProfile, this sets the amount of storage allocated, and you cannot exceed the allocated number of entries for any row. |
| pftype | [in] Whether to allocate storage dynamically (DynamicProfile) or statically (StaticProfile). |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 91 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::CrsMatrix | ( | const Teuchos::RCP< const map_type > & | rowMap, |
| const Teuchos::RCP< const map_type > & | colMap, | ||
| size_t | maxNumEntriesPerRow, | ||
| ProfileType | pftype = DynamicProfile, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Constructor specifying column Map and fixed number of entries for each row.
The column Map will be used to filter any matrix entries inserted using insertLocalValues() or insertGlobalValues().
| rowMap | [in] Distribution of rows of the matrix. |
| colMap | [in] Distribution of columns of the matrix. |
| maxNumEntriesPerRow | [in] Maximum number of matrix entries per row. If pftype==DynamicProfile, this is only a hint, and you can set this to zero without affecting correctness. If pftype==StaticProfile, this sets the amount of storage allocated, and you cannot exceed this number of entries in any row. |
| pftype | [in] Whether to allocate storage dynamically (DynamicProfile) or statically (StaticProfile). |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 123 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::CrsMatrix | ( | const Teuchos::RCP< const map_type > & | rowMap, |
| const Teuchos::RCP< const map_type > & | colMap, | ||
| const Teuchos::ArrayRCP< const size_t > & | NumEntriesPerRowToAlloc, | ||
| ProfileType | pftype = DynamicProfile, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) |
Constructor specifying column Map and number of entries in each row.
The column Map will be used to filter any matrix indices inserted using insertLocalValues() or insertGlobalValues().
| rowMap | [in] Distribution of rows of the matrix. |
| colMap | [in] Distribution of columns of the matrix. |
| NumEntriesPerRowToAlloc | [in] Maximum number of matrix entries to allocate for each row. If pftype==DynamicProfile, this is only a hint. If pftype==StaticProfile, this sets the amount of storage allocated, and you cannot exceed the allocated number of entries for any row. |
| pftype | [in] Whether to allocate storage dynamically (DynamicProfile) or statically (StaticProfile). |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 165 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
explicit |
Constructor specifying a previously constructed graph.
Calling this constructor fixes the graph structure of the sparse matrix. We say in this case that the matrix has a "static graph." If you create a CrsMatrix with this constructor, you are not allowed to insert new entries into the matrix, but you are allowed to change values in the matrix.
The given graph must be fill complete. Note that calling resumeFill() on the graph makes it not fill complete, even if you had previously called fillComplete() on the graph. In that case, you must call fillComplete() on the graph again before invoking this CrsMatrix constructor.
This constructor is marked explicit so that you can't create a CrsMatrix by accident when passing a CrsGraph into a function that takes a CrsMatrix.
| graph | [in] The graph structure of the sparse matrix. The graph must be fill complete. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 198 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::CrsMatrix | ( | const Teuchos::RCP< const map_type > & | rowMap, |
| const Teuchos::RCP< const map_type > & | colMap, | ||
| const typename local_matrix_type::row_map_type & | rowPointers, | ||
| const typename local_graph_type::entries_type::non_const_type & | columnIndices, | ||
| const typename local_matrix_type::values_type & | values, | ||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = null |
||
| ) |
Constructor specifying column Map and arrays containing the matrix in sorted local indices.
| rowMap | [in] Distribution of rows of the matrix. |
| colMap | [in] Distribution of columns of the matrix. |
| rowPointers | [in] The beginning of each row in the matrix, as in a CSR "rowptr" array. The length of this vector should be equal to the number of rows in the graph, plus one. This last entry should store the nunber of nonzeros in the matrix. |
| columnIndices | [in] The local indices of the columns, as in a CSR "colind" array. The length of this vector should be equal to the number of unknowns in the matrix. |
| values | [in] The local entries in the matrix, as in a CSR "vals" array. The length of this vector should be equal to the number of unknowns in the matrix. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 231 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::CrsMatrix | ( | const Teuchos::RCP< const map_type > & | rowMap, |
| const Teuchos::RCP< const map_type > & | colMap, | ||
| const Teuchos::ArrayRCP< size_t > & | rowPointers, | ||
| const Teuchos::ArrayRCP< LocalOrdinal > & | columnIndices, | ||
| const Teuchos::ArrayRCP< Scalar > & | values, | ||
| const Teuchos::RCP< ParameterList > & | params = null |
||
| ) |
Constructor specifying column Map and arrays containing the matrix in sorted, local ids.
| rowMap | [in] Distribution of rows of the matrix. |
| colMap | [in] Distribution of columns of the matrix. |
| rowPointers | [in] The beginning of each row in the matrix, as in a CSR "rowptr" array. The length of this vector should be equal to the number of rows in the graph, plus one. This last entry should store the nunber of nonzeros in the matrix. |
| columnIndices | [in] The local indices of the columns, as in a CSR "colind" array. The length of this vector should be equal to the number of unknowns in the matrix. |
| values | [in] The local entries in the matrix, as in a CSR "vals" array. The length of this vector should be equal to the number of unknowns in the matrix. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
| Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::CrsMatrix | ( | const Teuchos::RCP< const map_type > & | rowMap, |
| const Teuchos::RCP< const map_type > & | colMap, | ||
| const local_matrix_type & | lclMatrix, | ||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = null |
||
| ) |
Constructor specifying column Map and a local matrix, which the resulting CrsMatrix views.
Unlike most other CrsMatrix constructors, successful completion of this constructor will result in a fill-complete matrix.
| rowMap | [in] Distribution of rows of the matrix. |
| colMap | [in] Distribution of columns of the matrix. |
| lclMatrix | [in] A local CrsMatrix containing all local matrix values as well as a local graph. The graph's local row indices must come from the specified row Map, and its local column indices must come from the specified column Map. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Definition at line 304 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Destructor.
Definition at line 357 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
inline |
Create a deep copy of this CrsMatrix, where the copy may have a different Node type.
| node2 | [in] Kokkos Node instance for the returned copy. |
| params | [in/out] Optional list of parameters. If not null, any missing parameters will be filled in with their default values. |
Parameters to params:
true, create the copy with a static allocation profile. If false, use a dynamic allocation profile.true, fill clone using this matrix's column Map and local indices. This matrix must have a column Map in order for this to work. If false, fill clone using global indices. By default, this will use local indices only if this matrix is using local indices.true, call fillComplete() on the cloned CrsMatrix object, with parameters from the input parameters' "CrsMatrix" sublist The domain Map and range Map passed to fillComplete() are those of the map being cloned, if they exist. Otherwise, the row Map is used. Definition at line 401 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::insertGlobalValues | ( | const GlobalOrdinal | globalRow, |
| const Teuchos::ArrayView< const GlobalOrdinal > & | cols, | ||
| const Teuchos::ArrayView< const Scalar > & | vals | ||
| ) |
Insert one or more entries into the matrix, using global indices.
| globalRow | [in] Global index of the row into which to insert the entries. |
| cols | [in] Global indices of the columns into which to insert the entries. |
| values | [in] Values to insert into the above columns. |
For all k in 0, ..., col.size()-1, insert the value values[k] into entry (globalRow, cols[k]) of the matrix. If that entry already exists, add the new value to the old value.
This is a local operation. It does not communicate (using MPI). If row globalRow is owned by the calling process, the entries will be inserted immediately. Otherwise, if that row is not owned by the calling process, then the entries will be stored locally for now, and only communicated to the process that owns the row when either fillComplete() or globalAssemble() is called. If that process already has an entry, the incoming value will be added to the old value, just as if it were inserted on the owning process. If the matrix has a column Map (hasColMap() == true), and if globalRow is owned by process p, then it is forbidden to insert column indices that are not in the column Map on process p. Tpetra will test the input column indices to ensure this is the case, but if globalRow is not owned by the calling process, the test will be deferred until the next call to globalAssemble() or fillComplete().
It is legal to call this method whether the matrix's column indices are globally or locally indexed. If the matrix's column indices are locally indexed (isLocallyIndexed() == true), then this method will convert the input global column indices to local column indices.
For better performance when filling entries into a sparse matrix, consider the following tips:
Definition at line 1749 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::insertLocalValues | ( | const LocalOrdinal | localRow, |
| const ArrayView< const LocalOrdinal > & | cols, | ||
| const ArrayView< const Scalar > & | vals | ||
| ) |
Insert one or more entries into the matrix, using local indices.
| LocalRow | [in] Local index of the row into which to insert the entries. It must be owned by the row Map on the calling process. |
| cols | [in] Local indices of the columns into which to insert the entries. All of the column indices must be owned by the column Map on the calling process. |
| values | [in] Values to insert into the above columns. |
For all k in 0, ..., cols.size()-1, insert the value values[k] into entry (globalRow, cols[k]) of the matrix. If that entry already exists, add the new value to the old value.
In order to call this method, the matrix must be locally indexed, and it must have a column Map.
For better performance when filling entries into a sparse matrix, consider the following tips:
Definition at line 1515 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| LocalOrdinal Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::replaceGlobalValues | ( | GlobalOrdinal | globalRow, |
| const ArrayView< const GlobalOrdinal > & | cols, | ||
| const ArrayView< const Scalar > & | vals | ||
| ) |
Replace one or more entries' values, using global indices.
| globalRow | [in] Global index of the row in which to replace the entries. This row must be owned by the calling process. |
| cols | [in] Global indices of the columns in which to replace the entries. |
| vals | [in] Values to use for replacing the entries. |
For all k in 0, ..., cols.size()-1, replace the value at entry (globalRow, cols[k]) of the matrix with vals[k]. That entry must exist in the matrix already.
If (globalRow, cols[k]) corresponds to an entry that is duplicated in this matrix row (likely because it was inserted more than once and fillComplete() has not been called in the interim), the behavior of this method is not defined.
If the returned value N satisfies
0 <= N < cols.size(),
then cols.size() - N of the entries of cols are not valid global column indices. If the returned value is Teuchos::OrdinalTraits<LocalOrdinal>::invalid(), then at least one of the following is true:
! isFillActive () cols.size () != vals.size () Definition at line 2174 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| LocalOrdinal Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::replaceLocalValues | ( | const LocalOrdinal | localRow, |
| const ArrayView< const LocalOrdinal > & | cols, | ||
| const ArrayView< const Scalar > & | vals | ||
| ) |
Replace one or more entries' values, using local indices.
| localRow | [in] local index of the row in which to replace the entries. This row must be owned by the calling process. |
| cols | [in] Local indices of the columns in which to replace the entries. |
| vals | [in] Values to use for replacing the entries. |
For all k in 0, ..., cols.size()-1, replace the value at entry (localRow, cols[k]) of the matrix with vals[k]. That entry must exist in the matrix already.
If the returned value N satisfies
0 <= N < cols.size(),
then cols.size() - N of the entries of cols are not valid local column indices. If the returned value is Teuchos::OrdinalTraits<LocalOrdinal>::invalid(), then at least one of the following is true:
! isFillActive () ! hasColMap () cols.size () != vals.size () Definition at line 2068 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| LocalOrdinal Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::sumIntoGlobalValues | ( | const GlobalOrdinal | globalRow, |
| const ArrayView< const GlobalOrdinal > & | cols, | ||
| const ArrayView< const Scalar > & | vals | ||
| ) |
Sum into one or more sparse matrix entries, using global indices.
This is a local operation; it does not involve communication. However, if you sum into rows not owned by the calling process, it may result in future communication in globalAssemble() (which is called by fillComplete()).
If globalRow is owned by the calling process, then this method performs the sum-into operation right away. Otherwise, if the row is not owned by the calling process, this method defers the sum-into operation until globalAssemble(). That method communicates data for nonowned rows to the processes that own those rows. Then, globalAssemble() does one of the following:
| globalRow | [in] The global index of the row in which to sum into the matrix entries. |
| cols | [in] One or more column indices. |
| vals | [in] One or more values corresponding to those column indices. vals[k] corresponds to cols[k]. |
This method has the same preconditions and return value meaning as replaceGlobalValues() (which see).
Definition at line 2267 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| LocalOrdinal Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::sumIntoLocalValues | ( | const LocalOrdinal | localRow, |
| const ArrayView< const LocalOrdinal > & | cols, | ||
| const ArrayView< const Scalar > & | vals | ||
| ) |
Sum into one or more sparse matrix entries, using local indices.
| localRow | [in] Local index of a row. This row must be owned by the calling process. |
| cols | [in] Local indices of the columns whose entries we want to modify. |
| vals | [in] Values corresponding to the above column indices. vals[k] corresponds to cols[k]. |
This method has the same preconditions and return value meaning as replaceLocalValues() (which see).
Definition at line 2365 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::setAllToScalar | ( | const Scalar & | alpha | ) |
Set all matrix entries equal to alpha.
Definition at line 2817 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::scale | ( | const Scalar & | alpha | ) |
Scale the matrix's values: this := alpha*this.
Definition at line 2766 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::setAllValues | ( | const typename local_matrix_type::row_map_type & | rowPointers, |
| const typename local_graph_type::entries_type::non_const_type & | columnIndices, | ||
| const typename local_matrix_type::values_type & | values | ||
| ) |
Sets the 1D pointer arrays of the graph.
hasColMap() == true getGraph() != Teuchos::null Definition at line 2861 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::setAllValues | ( | const Teuchos::ArrayRCP< size_t > & | rowPointers, |
| const Teuchos::ArrayRCP< LocalOrdinal > & | columnIndices, | ||
| const Teuchos::ArrayRCP< Scalar > & | values | ||
| ) |
Sets the 1D pointer arrays of the graph.
hasColMap() == true getGraph() != Teuchos::null FIXME (mfh 24 Feb 2014) Why is the third prerequisites above different than the third prerequisite from the original class? The original is that fillComplete() must have been called.
Definition at line 2890 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::globalAssemble | ( | ) |
Communicate nonlocal contributions to other processes.
Users do not normally need to call this method. fillComplete always calls this method, unless you specifically tell fillComplete to do otherwise by setting its "No Nonlocal
Changes" parameter to true. Thus, it suffices to call fillComplete.
Methods like insertGlobalValues and sumIntoGlobalValues let you add or modify entries in rows that are not owned by the calling process. These entries are called "nonlocal contributions." The methods that allow nonlocal contributions store the entries on the calling process, until globalAssemble is called. globalAssemble sends these nonlocal contributions to the process(es) that own them, where they then become part of the matrix.
This method only does global assembly if there are nonlocal entries on at least one process. It does an all-reduce to find that out. If not, it returns early, without doing any more communication or work.
If you previously inserted into a row which is not owned by any process in the row Map, the behavior of this method is undefined. It may detect the invalid row indices and throw an exception, or it may silently drop the entries inserted into invalid rows. Behavior may vary, depending on whether Tpetra was built with debug checking enabled.
Definition at line 3452 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::resumeFill | ( | const RCP< ParameterList > & | params = null | ) |
Resume operations that may change the values or structure of the matrix.
This method must be called as a collective operation.
Calling fillComplete "freezes" both the values and the structure of the matrix. If you want to modify the matrix again, you must first call resumeFill. You then may not call resumeFill again on that matrix until you first call fillComplete. You may make sequences of fillComplete, resumeFill calls as many times as you wish.
isFillActive() && ! isFillComplete() Definition at line 3763 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::fillComplete | ( | const RCP< const map_type > & | domainMap, |
| const RCP< const map_type > & | rangeMap, | ||
| const RCP< ParameterList > & | params = null |
||
| ) |
Signal that data entry is complete, specifying domain and range maps.
Off-node indices are distributed (via globalAssemble()), indices are sorted, redundant indices are eliminated, and global indices are transformed to local indices.
isFillActive() == true isFillComplete()() == false isFillActive() == false isFillComplete() == trueParameters:
bool): Default is false. If true, the caller promises that no modifications to nonowned rows have happened on any process since the last call to fillComplete. This saves a global all-reduce to check whether any process did a nonlocal insert. Nonlocal changes include any sumIntoGlobalValues or insertGlobalValues call with a row index that is not in the row Map of the calling process.bool): Default is true. makeColMap() (which fillComplete may call) always groups remote GIDs by process rank, so that all remote GIDs with the same owning rank occur contiguously. By default, it always sorts remote GIDs in increasing order within those groups. This behavior differs from Epetra, which does not sort remote GIDs with the same owning process. If you don't want to sort (for compatibility with Epetra), set this parameter to false. This parameter only takes effect if the matrix owns the graph. This is an expert mode parameter ONLY. We make no promises about backwards compatibility of this parameter. It may change or disappear at any time. | void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::fillComplete | ( | const RCP< ParameterList > & | params = null | ) |
Signal that data entry is complete.
Off-node entries are distributed (via globalAssemble()), repeated entries are summed, and global indices are transformed to local indices.
isFillActive() == true isFillComplete()() == false isFillActive() == false isFillComplete() == true Definition at line 3819 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::expertStaticFillComplete | ( | const RCP< const map_type > & | domainMap, |
| const RCP< const map_type > & | rangeMap, | ||
| const RCP< const import_type > & | importer = Teuchos::null, |
||
| const RCP< const export_type > & | exporter = Teuchos::null, |
||
| const RCP< ParameterList > & | params = Teuchos::null |
||
| ) |
Perform a fillComplete on a matrix that already has data.
The matrix must already have filled local 1-D storage (k_clInds1D_ and k_rowPtrs_ for the graph, and k_values1D_ in the matrix). If the matrix has been constructed in any other way, this method will throw an exception. This routine is needed to support other Trilinos packages and should not be called by ordinary users.
Definition at line 4001 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::replaceColMap | ( | const Teuchos::RCP< const map_type > & | newColMap | ) |
Replace the matrix's column Map with the given Map.
| newColMap | [in] New column Map. Must be nonnull. |
Definition at line 3348 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::reindexColumns | ( | crs_graph_type *const | graph, |
| const Teuchos::RCP< const map_type > & | newColMap, | ||
| const Teuchos::RCP< const import_type > & | newImport = Teuchos::null, |
||
| const bool | sortEachRow = true |
||
| ) |
Reindex the column indices in place, and replace the column Map. Optionally, replace the Import object as well.
! this->isFillComplete() . NULL, or it is not fill complete: graph == NULL || ! graph->isFillComplete(). | graph | [in] The matrix's graph. If you don't provide this (i.e., if graph == NULL), then the matrix must own its graph, which will be modified in place. (That is, you must not have created the matrix with a constant graph.) If you do provide this, then the method will assume that it is the same graph as the matrix's graph, and the provided graph will be modified in place. |
| newColMap | [in] New column Map. Must be nonnull. |
| newImport | [in] New Import object. Optional; computed if not provided or if null. Computing an Import is expensive, so it is worth providing this if you can. |
| sortEachRow | [in] If true, sort the indices (and their corresponding values) in each row after reindexing. |
Why would you want to use this method? Well, for example, you might need to use an Ifpack2 preconditioner that only accepts a matrix with a certain kind of column Map. Your matrix has the wrong kind of column Map, but you know how to compute the right kind of column Map. You might also know an efficient way to compute an Import object from the current domain Map to the new column Map. (For an instance of the latter, see the Details::makeOptimizedColMapAndImport function in Tpetra_Details_makeOptimizedColMap.hpp.)
Suppose that you created this CrsMatrix with a constant graph; that is, that you called the CrsMatrix constructor that takes a CrsGraph as input:
Now suppose that you want to give A to a preconditioner that can't handle a matrix with an arbitrary column Map (in the example above, origColMap). You first must create a new suitable column Map newColMap, and optionally a new Import object newImport from the matrix's current domain Map to the new column Map. Then, call this method, passing in G (which must not be fill complete) while the matrix is not fill complete. Be sure to save the graph's original Import object; you'll need that later.
Now you may give the matrix A to the preconditioner in question. After doing so, and after you solve the linear system using the preconditioner, you might want to put the matrix back like it originally was. You can do that, too!
Definition at line 3368 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::replaceDomainMapAndImporter | ( | const Teuchos::RCP< const map_type > & | newDomainMap, |
| Teuchos::RCP< const import_type > & | newImporter | ||
| ) |
Replace the current domain Map and Import with the given objects.
| newDomainMap | [in] New domain Map. Must be nonnull. |
| newImporter | [in] Optional Import object. If null, we will compute it. |
isFillComplete() == true. Definition at line 3402 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Remove processes owning zero rows from the Maps and their communicator.
| newMap | [in] This must be the result of calling the removeEmptyProcesses() method on the row Map. If it is not, this method's behavior is undefined. This pointer will be null on excluded processes. |
Definition at line 6508 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The communicator over which the matrix is distributed.
Definition at line 368 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The Kokkos Node instance.
Definition at line 380 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The Map that describes the row distribution in this matrix.
Definition at line 569 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The Map that describes the column distribution in this matrix.
Definition at line 578 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
This matrix's graph, as a RowGraph.
Definition at line 620 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| Teuchos::RCP< const CrsGraph< LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > > > Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::getCrsGraph | ( | ) | const |
This matrix's graph, as a CrsGraph.
Definition at line 637 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
inline |
The local sparse matrix.
Definition at line 1183 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
virtual |
Number of global elements in the row map of this matrix.
This is <it>not</it> the number of rows in the matrix as a mathematical object. This method returns the global sum of the number of local elements in the row map on each processor, which is the row map's getGlobalNumElements(). Since the row map is not one-to-one in general, that global sum could be different than the number of rows in the matrix. If you want the number of rows in the matrix, ask the range map for its global number of elements, using the following code: global_size_t globalNumRows = getRangeMap()->getGlobalNumElements(); This method retains the behavior of Epetra, which also asks the row map for the global number of rows, rather than asking the range map.
Definition at line 470 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The number of global columns in the matrix.
This equals the number of entries in the matrix's domain Map.
Definition at line 479 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The number of matrix rows owned by the calling process.
Note that the sum of all the return values over all processes in the row Map's communicator does not necessarily equal the global number of rows in the matrix, if the row Map is overlapping.
Definition at line 488 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The number of columns connected to the locally owned rows of this matrix.
Throws std::runtime_error if ! hasColMap ().
Definition at line 497 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The index base for global indices for this matrix.
Definition at line 560 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The global number of entries in this matrix.
Definition at line 452 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The local number of entries in this matrix.
Definition at line 461 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Returns the current number of entries on this node in the specified global row.
Returns OrdinalTraits<size_t>::invalid() if the specified global row does not belong to this matrix.
Definition at line 524 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Returns the current number of entries on this node in the specified local row.
Returns OrdinalTraits<size_t>::invalid() if the specified local row is not valid for this matrix.
Definition at line 533 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Returns the number of global diagonal entries, based on global row/column index comparisons.
Undefined if isFillActive().
Definition at line 506 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Returns the number of local diagonal entries, based on global row/column index comparisons.
Undefined if isFillActive().
Definition at line 515 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Returns the maximum number of entries across all rows/columns on all nodes.
Undefined if isFillActive().
Definition at line 542 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Returns the maximum number of entries across all rows/columns on this node.
Undefined if isFillActive().
Definition at line 551 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Indicates whether the matrix has a well-defined column map.
Definition at line 443 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Indicates whether the matrix is lower triangular.
Undefined if isFillActive().
Definition at line 652 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Indicates whether the matrix is upper triangular.
Undefined if isFillActive().
Definition at line 664 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Whether the matrix is locally indexed on the calling process.
The matrix is locally indexed on the calling process if and only if all of the following hold:
The following is always true:
That is, a matrix may be neither locally nor globally indexed, but it can never be both. Furthermore a matrix that is not fill complete, might have some processes that are neither locally nor globally indexed, and some processes that are globally indexed. The processes that are neither do not have any entries.
Definition at line 425 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Whether the matrix is globally indexed on the calling process.
The matrix is globally indexed on the calling process if and only if all of the following hold:
The following is always true:
That is, a matrix may be neither locally nor globally indexed, but it can never be both. Furthermore a matrix that is not fill complete, might have some processes that are neither locally nor globally indexed, and some processes that are globally indexed. The processes that are neither do not have any entries.
Definition at line 434 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Whether the matrix is fill complete.
A matrix is fill complete (or "in compute mode") when fillComplete() has been called without an intervening call to resumeFill(). A matrix must be fill complete in order to call computational kernels like sparse matrix-vector multiply and sparse triangular solve. A matrix must be not fill complete ("in edit mode") in order to call methods that insert, modify, or remove entries.
The following are always true:
A matrix starts out (after its constructor returns) as not fill complete. It becomes fill complete after fillComplete() returns, and becomes not fill complete again if resumeFill() is called. Some methods like clone() and some of the "nonmember constructors" (like importAndFillComplete() and exportAndFillComplete()) may return a fill-complete matrix.
Definition at line 398 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| bool Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::isFillActive | ( | ) | const |
Whether the matrix is not fill complete.
A matrix is fill complete (or "in compute mode") when fillComplete() has been called without an intervening call to resumeFill(). A matrix must be fill complete in order to call computational kernels like sparse matrix-vector multiply and sparse triangular solve. A matrix must be not fill complete ("in edit mode") in order to call methods that insert, modify, or remove entries.
The following are always true:
A matrix starts out (after its constructor returns) as not fill complete. It becomes fill complete after fillComplete() returns, and becomes not fill complete again if resumeFill() is called. Some methods like clone() and some of the "nonmember constructors" (like importAndFillComplete() and exportAndFillComplete()) may return a fill-complete matrix.
Definition at line 407 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| bool Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::isStorageOptimized | ( | ) | const |
Returns true if storage has been optimized.
Optimized storage means that the allocation of each row is equal to the number of entries. The effect is that a pass through the matrix, i.e., during a mat-vec, requires minimal memory traffic. One limitation of optimized storage is that no new indices can be added to the matrix.
Definition at line 416 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| ProfileType Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::getProfileType | ( | ) | const |
Returns true if the matrix was allocated with static data structures.
Definition at line 389 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| bool Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::isStaticGraph | ( | ) | const |
Indicates that the graph is static, so that new entries cannot be added to this matrix.
Definition at line 676 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Compute and return the Frobenius norm of the matrix.
The Frobenius norm of the matrix is defined as [ |A|_F = {{i,j} |A(i,j)|^2}. ].
If the matrix is fill complete, then the computed value is cached; the cache is cleared whenever resumeFill() is called. Otherwise, the value is computed every time the method is called.
Definition at line 3280 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Return true if getLocalRowView() and getGlobalRowView() are valid for this object.
Definition at line 700 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Fill given arrays with a deep copy of the locally owned entries of the matrix in a given row, using global column indices.
| GlobalRow | [in] Global index of the row for which to return entries. |
| Indices | [out] Global column indices corresponding to values. |
| Values | [out] Matrix values. |
| NumEntries | [out] Number of entries. |
Scalar or impl_scalar_type for output array of matrix values.If Scalar differs from impl_scalar_type, as for example with std::complex<T> and Kokkos::complex<T>, we must choose which type to use. We must make the same choice as RowMatrix does, else CrsMatrix won't compile, because it won't implement a pure virtual method. We choose Scalar, for the following reasons. First, Scalar is the user's preferred type, and impl_scalar_type an implementation detail that makes Tpetra work with Kokkos. Second, Tpetra's public interface provides a host-only interface, which eliminates some reasons for requiring implementation-specific types like Kokkos::complex.
We do eventually want to put Tpetra methods in Kokkos kernels, but we only need to put them in host kernels, since Tpetra is a host-only interface. Users can still manually handle conversion from Scalar to impl_scalar_type for reductions.
The right thing to do would be to rewrite RowMatrix so that getGlobalRowCopy is NOT inherited, but is implemented by a pure virtual "hook" getGlobalRowCopyImpl. The latter takes raw pointers. That would give us the freedom to overload getGlobalRowCopy, which one normally can't do with virtual methods. It would make sense for one getGlobalRowCopyImpl method to implement both Teuchos::ArrayView and Kokos::View versions of getGlobalRowCopy.
Note: A std::runtime_error exception is thrown if either Indices or Values is not large enough to hold the data associated with row GlobalRow. If row GlobalRow is not owned by the calling process, then Indices and Values are unchanged and NumIndices is returned as Teuchos::OrdinalTraits<size_t>::invalid().
Definition at line 2593 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Fill given arrays with a deep copy of the locally owned entries of the matrix in a given row, using local column indices.
| localRow | [in] Local index of the row for which to return entries. |
| colInds | [out] Local column indices corresponding to values. |
| vals | [out] Matrix values. |
| numEntries | [out] Number of entries returned. |
Note: A std::runtime_error exception is thrown if either colInds or vals is not large enough to hold the data associated with row localRow. If row localRow is not owned by the calling process, then colInds and vals are unchanged and numEntries is returned as Teuchos::OrdinalTraits<size_t>::invalid().
Definition at line 2522 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::getGlobalRowView | ( | GlobalOrdinal | GlobalRow, |
| Teuchos::ArrayView< const GlobalOrdinal > & | indices, | ||
| Teuchos::ArrayView< const Scalar > & | values | ||
| ) | const |
Get a constant, nonpersisting view of a row of this matrix, using global row and column indices.
| GlobalRow | [in] Global index of the row to view. |
| indices | [out] On output: view of the global column indices in the row. |
| values | [out] On output: view of the values in the row. |
isLocallyIndexed () == false indices.size () == this->getNumEntriesInGlobalRow (GlobalRow)If GlobalRow is not a valid global row index on the calling process, then indices is set to null.
Definition at line 2724 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::getLocalRowView | ( | LocalOrdinal | LocalRow, |
| Teuchos::ArrayView< const LocalOrdinal > & | indices, | ||
| Teuchos::ArrayView< const Scalar > & | values | ||
| ) | const |
Get a constant, nonpersisting view of a row of this matrix, using local row and column indices.
| LocalRow | [in] Local index of the row to view. |
| indices | [out] On output: view of the local column indices in the row. |
| values | [out] On output: view of the values in the row. |
isGloballyIndexed () == false indices.size () == this->getNumEntriesInLocalRow (LocalRow)If LocalRow is not a valid local row index on the calling process, then indices is set to null.
Definition at line 2660 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::getLocalDiagCopy | ( | Vector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | diag | ) | const |
Get a copy of the diagonal entries of the matrix.
This method returns a Vector with the same Map as this matrix's row Map. On each process, it contains the diagonal entries owned by the calling process.
Definition at line 3017 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::getLocalDiagOffsets | ( | Teuchos::ArrayRCP< size_t > & | offsets | ) | const |
Get offsets of the diagonal entries in the matrix.
offsets.size() == getNodeNumRows()This method creates an array of offsets of the local diagonal entries in the matrix. This array is suitable for use in the two-argument version of getLocalDiagCopy(). However, its contents are not defined in any other context. For example, you should not rely on offsets[i] being the index of the diagonal entry in the views returned by getLocalRowView(). This may be the case, but it need not be. (For example, we may choose to optimize the lookups down to the optimized storage level, in which case the offsets will be computed with respect to the underlying storage format, rather than with respect to the views.)
Calling any of the following invalidates the output array:
If the matrix has a const ("static") graph, and if that graph is fill complete, then the offsets array remains valid through calls to fillComplete() and resumeFill(). "Invalidates" means that you must call this method again to recompute the offsets.
Definition at line 2921 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::getLocalDiagCopy | ( | Vector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | diag, |
| const Teuchos::ArrayView< const size_t > & | offsets | ||
| ) | const |
Variant of getLocalDiagCopy() that uses precomputed offsets.
This method uses the offsets of the diagonal entries, as precomputed by getLocalDiagOffsets(), to speed up copying the diagonal of the matrix. The offsets must be recomputed if any of the following methods are called:
If the matrix has a const ("static") graph, and if that graph is fill complete, then the offsets array remains valid through calls to fillComplete() and resumeFill().
Definition at line 3097 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::leftScale | ( | const Vector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | x | ) |
Definition at line 3159 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::rightScale | ( | const Vector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | x | ) |
Definition at line 3221 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
inline |
Compute a sparse matrix-MultiVector product local to each process.
This method computes the local part of Y := beta*Y
Op(A) is either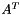 
, 
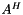(the transpose), or 
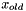(the conjugate transpose). "The local part" means that this method does no communication between processes, even if this is necessary for correctness of the matrix-vector multiply. Use the apply() method if you want to compute the mathematical sparse matrix-vector multiply.This method is mainly of use to Tpetra developers, though some users may find it helpful if they plan to reuse the result of doing an Import on the input MultiVector for several sparse matrix-vector multiplies with matrices that have the same column Map.
When Op(A) is 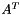(trans == Teuchos::NO_TRANS), then X's Map must be the same as the column Map of this matrix, and Y's Map must be the same as the row Map of this matrix. We say in this case that X is "post-Imported," and Y is "pre-Exported." When Op(A) is 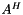or 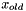(trans is Teuchos::TRANS or Teuchos::CONJ_TRANS, then X's Map must be the same as the row Map of this matrix, and Y's Map must be the same as the column Map of this matrix.
Both X and Y must have constant stride, and they may not alias one another (that is, occupy overlapping space in memory). We may not necessarily check for aliasing, and if we do, we will only do this in a debug build. Aliasing X and Y may cause nondeterministically incorrect results.
This method is templated on the type of entries in both the input MultiVector (DomainScalar) and the output MultiVector (RangeScalar). Thus, this method works for MultiVector objects of arbitrary type. However, this method only performs computation local to each MPI process. Use CrsMatrixMultiplyOp to handle global communication (the Import and Export operations for the input resp. output MultiVector), if you have a matrix with entries of a different type than the input and output MultiVector objects.
If beta == 0, this operation will enjoy overwrite semantics: Y will be overwritten with the result of the multiplication, even if it contains NaN (not-a-number) floating-point entries. Otherwise, the multiply result will be accumulated into Y.
Definition at line 1641 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
inline |
Gauss-Seidel or SOR on .
Apply a forward or backward sweep of Gauss-Seidel or Successive Over-Relaxation (SOR) to the linear system(s) . For Gauss-Seidel, set the damping factor omega to 1.
| DomainScalar | The type of entries in the input multivector X. This may differ from the type of entries in A or in B. |
| RangeScalar | The type of entries in the output multivector B. This may differ from the type of entries in A or in X. |
| B | [in] Right-hand side(s). |
| X | [in/out] On input: initial guess(es). On output: result multivector(s). |
| D | [in] Inverse of diagonal entries of the matrix A. |
| omega | [in] SOR damping factor. omega = 1 results in Gauss-Seidel. |
| direction | [in] Sweep direction: KokkosClassic::Forward or KokkosClassic::Backward. ("Symmetric" requires interprocess communication (before each sweep), which is not part of the local kernel.) |
Definition at line 1750 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
inline |
Reordered Gauss-Seidel or SOR on .
Apply a forward or backward sweep of reordered Gauss-Seidel or Successive Over-Relaxation (SOR) to the linear system(s) . For Gauss-Seidel, set the damping factor omega to 1. The ordering can be a partial one, in which case the Gauss-Seidel is only executed on a local subset of unknowns.
| DomainScalar | The type of entries in the input multivector X. This may differ from the type of entries in A or in B. |
| RangeScalar | The type of entries in the output multivector B. This may differ from the type of entries in A or in X. |
| B | [in] Right-hand side(s). |
| X | [in/out] On input: initial guess(es). On output: result multivector(s). |
| D | [in] Inverse of diagonal entries of the matrix A. |
| rowIndices | [in] Ordered list of indices on which to execute GS. |
| omega | [in] SOR damping factor. omega = 1 results in Gauss-Seidel. |
| direction | [in] Sweep direction: KokkosClassic::Forward or KokkosClassic::Backward. ("Symmetric" requires interprocess communication (before each sweep), which is not part of the local kernel.) |
Definition at line 1837 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
inline |
Solves a linear system when the underlying matrix is locally triangular.
X is required to be post-imported, i.e., described by the column map of the matrix. Y is required to be pre-exported, i.e., described by the row map of the matrix.
This method is templated on the scalar type of MultiVector objects, allowing this method to be applied to MultiVector objects of arbitrary type. However, if you intend to use this with template parameters not equal to Scalar, we recommend that you wrap this matrix in a CrsMatrixSolveOp. That class will handle the Import/Export operations required to apply a matrix with non-trivial communication needs.
Both X and Y are required to have constant stride. However, unlike multiply(), it is permissible for &X == &Y. No run-time checking will be performed in a non-debug build.
Definition at line 1926 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| Teuchos::RCP<CrsMatrix<T, LocalOrdinal, GlobalOrdinal, node_type> > Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::convert | ( | ) | const |
Return another CrsMatrix with the same entries, but converted to a different Scalar type T.
|
virtual |
Compute a sparse matrix-MultiVector multiply.
This method computes Y := beta*Y + alpha*Op(A)*X, where Op(A) is either 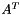, 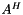(the transpose), or 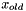(the conjugate transpose).
If beta == 0, this operation will enjoy overwrite semantics: Y's entries will be ignored, and Y will be overwritten with the result of the multiplication, even if it contains NaN (not-a-number) floating-point entries.
Definition at line 4422 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Whether apply() allows applying the transpose or conjugate transpose.
Reimplemented from Tpetra::Operator< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >.
Definition at line 688 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The domain Map of this matrix.
This method implements Tpetra::Operator. If fillComplete() has not yet been called at least once on this matrix, or if the matrix was not constructed with a domain Map, then this method returns Teuchos::null.
Definition at line 592 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
The range Map of this matrix.
This method implements Tpetra::Operator. If fillComplete() has not yet been called at least once on this matrix, or if the matrix was not constructed with a domain Map, then this method returns Teuchos::null.
Definition at line 606 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::gaussSeidel | ( | const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | B, |
| MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | X, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | D, | ||
| const Scalar & | dampingFactor, | ||
| const ESweepDirection | direction, | ||
| const int | numSweeps | ||
| ) | const |
"Hybrid" Jacobi + (Gauss-Seidel or SOR) on .
"Hybrid" means Successive Over-Relaxation (SOR) or Gauss-Seidel within an (MPI) process, but Jacobi between processes. Gauss-Seidel is a special case of SOR, where the damping factor is one.
The Forward or Backward sweep directions have their usual SOR meaning within the process. Interprocess communication occurs once before the sweep, as it normally would in Jacobi.
The Symmetric sweep option means two sweeps: first Forward, then Backward. Interprocess communication occurs before each sweep, as in Jacobi. Thus, Symmetric results in two interprocess communication steps.
| B | [in] Right-hand side(s). |
| X | [in/out] On input: initial guess(es). On output: result multivector(s). |
| D | [in] Inverse of diagonal entries of the matrix A. |
| dampingFactor | [in] SOR damping factor. A damping factor of one results in Gauss-Seidel. |
| direction | [in] Sweep direction: Forward, Backward, or Symmetric. |
| numSweeps | [in] Number of sweeps. We count each Symmetric sweep (including both its Forward and its Backward sweep) as one. |
This method has the following requirements:
#1 is just the usual requirement for operators: the input multivector must always be in the domain Map. The Gauss-Seidel kernel imposes additional requirements, since it
#3 is reasonable if the matrix constructed the column Map, because the method that does this (CrsGraph::makeColMap) puts the local GIDs (those in the domain Map) in front and the remote GIDs (not in the domain Map) at the end of the column Map. However, if you constructed the column Map yourself, you are responsible for maintaining this invariant. #6 lets us do the Import from the domain Map to the column Map in place.
The Gauss-Seidel kernel also assumes that each process has the entire value (not a partial value to sum) of all the diagonal elements in the rows in its row Map. (We guarantee this anyway though the separate D vector.) This is because each element of the output multivector depends nonlinearly on the diagonal elements. Shared ownership of off-diagonal elements would produce different results.
Definition at line 4456 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::reorderedGaussSeidel | ( | const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | B, |
| MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | X, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | D, | ||
| const Teuchos::ArrayView< LocalOrdinal > & | rowIndices, | ||
| const Scalar & | dampingFactor, | ||
| const ESweepDirection | direction, | ||
| const int | numSweeps | ||
| ) | const |
Reordered "Hybrid" Jacobi + (Gauss-Seidel or SOR) on .
"Hybrid" means Successive Over-Relaxation (SOR) or Gauss-Seidel within an (MPI) process, but Jacobi between processes. Gauss-Seidel is a special case of SOR, where the damping factor is one. The ordering can be a partial one, in which case the Gauss-Seidel is only executed on a local subset of unknowns.
The Forward or Backward sweep directions have their usual SOR meaning within the process. Interprocess communication occurs once before the sweep, as it normally would in Jacobi.
The Symmetric sweep option means two sweeps: first Forward, then Backward. Interprocess communication occurs before each sweep, as in Jacobi. Thus, Symmetric results in two interprocess communication steps.
| B | [in] Right-hand side(s). |
| X | [in/out] On input: initial guess(es). On output: result multivector(s). |
| D | [in] Inverse of diagonal entries of the matrix A. |
| rowIndices | [in] Ordered list of indices on which to execute GS. |
| dampingFactor | [in] SOR damping factor. A damping factor of one results in Gauss-Seidel. |
| direction | [in] Sweep direction: Forward, Backward, or Symmetric. |
| numSweeps | [in] Number of sweeps. We count each Symmetric sweep (including both its Forward and its Backward sweep) as one. |
This method has the following requirements:
#1 is just the usual requirement for operators: the input multivector must always be in the domain Map. The Gauss-Seidel kernel imposes additional requirements, since it
#3 is reasonable if the matrix constructed the column Map, because the method that does this (CrsGraph::makeColMap) puts the local GIDs (those in the domain Map) in front and the remote GIDs (not in the domain Map) at the end of the column Map. However, if you constructed the column Map yourself, you are responsible for maintaining this invariant. #6 lets us do the Import from the domain Map to the column Map in place.
The Gauss-Seidel kernel also assumes that each process has the entire value (not a partial value to sum) of all the diagonal elements in the rows in its row Map. (We guarantee this anyway though the separate D vector.) This is because each element of the output multivector depends nonlinearly on the diagonal elements. Shared ownership of off-diagonal elements would produce different results.
Definition at line 4474 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::gaussSeidelCopy | ( | MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | X, |
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | B, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | D, | ||
| const Scalar & | dampingFactor, | ||
| const ESweepDirection | direction, | ||
| const int | numSweeps, | ||
| const bool | zeroInitialGuess | ||
| ) | const |
Version of gaussSeidel(), with fewer requirements on X.
This method is just like gaussSeidel(), except that X need only be in the domain Map. This method does not require that X be a domain Map view of a column Map multivector. As a result, this method must copy X into a domain Map multivector before operating on it.
| X | [in/out] On input: initial guess(es). On output: result multivector(s). |
| B | [in] Right-hand side(s), in the range Map. |
| D | [in] Inverse of diagonal entries of the matrix, in the row Map. |
| dampingFactor | [in] SOR damping factor. A damping factor of one results in Gauss-Seidel. |
| direction | [in] Sweep direction: Forward, Backward, or Symmetric. |
| numSweeps | [in] Number of sweeps. We count each Symmetric sweep (including both its Forward and its Backward sweep) as one. |
| zeroInitialGuess | [in] If true, this method will fill X with zeros initially. If false, this method will assume that X contains a possibly nonzero initial guess on input. Note that a nonzero initial guess may impose an additional nontrivial communication cost (an additional Import). |
Definition at line 4748 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::reorderedGaussSeidelCopy | ( | MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | X, |
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | B, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, node_type > & | D, | ||
| const Teuchos::ArrayView< LocalOrdinal > & | rowIndices, | ||
| const Scalar & | dampingFactor, | ||
| const ESweepDirection | direction, | ||
| const int | numSweeps, | ||
| const bool | zeroInitialGuess | ||
| ) | const |
Version of reorderedGaussSeidel(), with fewer requirements on X.
This method is just like reorderedGaussSeidel(), except that X need only be in the domain Map. This method does not require that X be a domain Map view of a column Map multivector. As a result, this method must copy X into a domain Map multivector before operating on it.
| X | [in/out] On input: initial guess(es). On output: result multivector(s). |
| B | [in] Right-hand side(s), in the range Map. |
| D | [in] Inverse of diagonal entries of the matrix, in the row Map. |
| rowIndices | [in] Ordered list of indices on which to execute GS. |
| dampingFactor | [in] SOR damping factor. A damping factor of one results in Gauss-Seidel. |
| direction | [in] Sweep direction: Forward, Backward, or Symmetric. |
| numSweeps | [in] Number of sweeps. We count each Symmetric sweep (including both its Forward and its Backward sweep) as one. |
| zeroInitialGuess | [in] If true, this method will fill X with zeros initially. If false, this method will assume that X contains a possibly nonzero initial guess on input. Note that a nonzero initial guess may impose an additional nontrivial communication cost (an additional Import). |
Definition at line 4768 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Implementation of RowMatrix::add: return alpha*A + beta*this.
This override of the default implementation ensures that, when called on a CrsMatrix, this method always returns a CrsMatrix of exactly the same type as *this. "Exactly the same
type" means that all the template parameters match, including the fifth template parameter. The input matrix A need not necessarily be a CrsMatrix or a CrsMatrix of the same type as *this, though this method may be able to optimize further in that case.
Reimplemented from Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >.
Definition at line 6537 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| std::string Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::description | ( | ) | const |
A one-line description of this object.
Definition at line 5282 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::describe | ( | Teuchos::FancyOStream & | out, |
| const Teuchos::EVerbosityLevel | verbLevel = Teuchos::Describable::verbLevel_default |
||
| ) | const |
Print the object with some verbosity level to an FancyOStream object.
Definition at line 5313 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::unpackAndCombine | ( | const Teuchos::ArrayView< const LocalOrdinal > & | importLIDs, |
| const Teuchos::ArrayView< const char > & | imports, | ||
| const Teuchos::ArrayView< size_t > & | numPacketsPerLID, | ||
| size_t | constantNumPackets, | ||
| Distributor & | distor, | ||
| CombineMode | combineMode | ||
| ) |
Unpack the imported column indices and values, and combine into matrix.
combineMode depends on whether the matrix's graph is static or dynamic. ADD, REPLACE, and ABSMAX are valid for a static graph, but INSERT is not. ADD and INSERT are valid for a dynamic graph; ABSMAX and REPLACE have not yet been implemented (and would require serious changes to matrix assembly in order to implement sensibly). Definition at line 6157 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
virtual |
Pack this object's data for an Import or Export.
| exportLIDs | [in] Local indices of the rows to pack. |
| exports | [out] On output: array of packed matrix entries; allocated by method. |
| numPacketsPerLID | [out] On output: numPacketsPerLID[i] is the number of bytes of the exports array used for storing packed local row exportLIDs[i]. |
| constantNumPackets | [out] If zero on output, the packed rows may have different numbers of entries. If nonzero on output, then that number gives the constant number of entries for all packed rows on all processes in the matrix's communicator. |
| distor | [in/out] The Distributor object which implements the Import or Export operation that is calling this method. |
The number of "packets" per row is the number of bytes per row. Each row has the following storage format:
[numEnt, vals, inds],
where:
numEnt (LocalOrdinal): number of entries in the row. vals: array of Scalar. For the k-th entry in the row, vals[k] is its value and inds[k] its global column index. inds: array of GlobalOrdinal. For the k-th entry in the row, vals[k] is its value and inds[k] its global column index. We reserve the right to pad for alignment in the future. In that case, the number of bytes reported by numPacketsPerLID will reflect padding to align each datum to its size, and the row will have final padding as well to ensure that the next row is aligned. Rows with zero entries will still take zero bytes, however.
RowMatrix::pack will always use the same packing scheme as this method. This ensures correct Import / Export from a RowMatrix to a CrsMatrix.
We do not recommend relying on the details of this packing scheme. We describe it here more for Tpetra developers and less for users.
DistObject requires packing an object's entries as type Packet, which is the first template parameter of DistObject. Since sparse matrices have both values and indices, we use Packet=char and pack them into buffers of char (really "byte"). Indices are stored as global indices, in case the source and target matrices have different column Maps (or don't have a column Map yet).
Currently, we only pack values and column indices. Row indices are stored implicitly as the local indices (LIDs) to pack (see exportLIDs). This is because a DistObject instance only has one Map, and currently we use the row Map for CrsMatrix (and RowMatrix). This makes redistribution of matrices with 2-D distributions less efficient, but it works for now. This may change in the future.
On output, numPacketsPerLID[i] gives the number of bytes used to pack local row exportLIDs[i] of this object (the source object of an Import or Export). If offset is the exclusive prefix sum-scan of numPacketsPerLID, then on output, exports[offset[i] .. offset[i+1]] (half-exclusive range) contains the packed entries for local row exportLIDs[i].
Entries for each row use a "struct of arrays" pattern to match how sparse matrices actually store their data. The number of entries in the row goes first, all values go next, and all column indices (stored as global indices) go last. Values and column indices occur in the same order. Rows with zero entries always take zero bytes (we do not store their number of entries explicitly). This ensures sparsity of storage and communication in case most rows are empty.
GCC >= 4.9 and recent-future versions of the Intel compiler implement stricter aliasing rules that forbid unaligned type punning. If we were to pack as an "array of structs" – in this case, an array of (Scalar, GlobalOrdinal) pairs – then we would either have to pad each matrix entry for alignment, or call memcpy twice per matrix entry to pack and unpack. The "struct of arrays" storage scheme reduces the padding requirement to a constant per row, or reduces the number of memcpy calls to two per row.
We include the number of entries in each row in that row's packed data, to make unpacking easier. This saves us from an error-prone computation to find the number of entries from the number of bytes. That computation gets even more difficult if we have to introduce padding for alignment in the future. Knowing the number of entries for each row also makes parallelizing packing and unpacking easier.
sizeof(Scalar) says how much data were used to represent a Scalar in its packed form. sizeof returns the same value on all processes for Scalar, LocalOrdinal, and GlobalOrdinal. Reimplemented from Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType > >.
Definition at line 5963 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
inline |
Get the Kokkos local values.
Definition at line 2555 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::importAndFillComplete | ( | Teuchos::RCP< CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, node_type > > & | destMatrix, |
| const import_type & | importer, | ||
| const Teuchos::RCP< const map_type > & | domainMap, | ||
| const Teuchos::RCP< const map_type > & | rangeMap, | ||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) | const |
Import from this to the given destination matrix, and make the result fill complete.
If destMatrix.is_null(), this creates a new matrix as the destination. (This is why destMatrix is passed in by nonconst reference to RCP.) Otherwise it checks for "pristine" status and throws if that is not the case. "Pristine" means that the matrix has no entries and is not fill complete.
Use of the "non-member constructor" version of this method, exportAndFillCompleteCrsMatrix, is preferred for user applications.
Definition at line 7383 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
| void Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Kokkos::Compat::KokkosDeviceWrapperNode< DeviceType >, false >::exportAndFillComplete | ( | Teuchos::RCP< CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, node_type > > & | destMatrix, |
| const export_type & | exporter, | ||
| const Teuchos::RCP< const map_type > & | domainMap = Teuchos::null, |
||
| const Teuchos::RCP< const map_type > & | rangeMap = Teuchos::null, |
||
| const Teuchos::RCP< Teuchos::ParameterList > & | params = Teuchos::null |
||
| ) | const |
Export from this to the given destination matrix, and make the result fill complete.
If destMatrix.is_null(), this creates a new matrix as the destination. (This is why destMatrix is passed in by nonconst reference to RCP.) Otherwise it checks for "pristine" status and throws if that is not the case. "Pristine" means that the matrix has no entries and is not fill complete.
Use of the "non-member constructor" version of this method, exportAndFillCompleteCrsMatrix, is preferred for user applications.
Definition at line 7401 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Allocate values (and optionally indices) using the Node.
| gas | [in] If GraphNotYetAllocated, allocate the indices of myGraph_ via allocateIndices(lg) before allocating values. |
| lg | [in] Argument passed into myGraph_->allocateIndices(), if applicable. |
Definition at line 712 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Sort the entries of each row by their column indices.
This only does anything if the graph isn't already sorted (i.e., ! myGraph_->isSorted ()). This method is called in fillComplete().
Definition at line 4070 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Merge entries in each row with the same column indices.
This only does anything if the graph isn't already merged (i.e., ! myGraph_->isMerged ()). This method is called in fillComplete().
Definition at line 4095 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Clear matrix properties that require collectives.
This clears whatever computeGlobalConstants() (which see) computed, in preparation for changes to the matrix. The current implementation of this method does nothing.
This method is called in resumeFill().
Definition at line 3799 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Compute matrix properties that require collectives.
The corresponding Epetra_CrsGraph method computes things like the global number of nonzero entries, that require collectives over the matrix's communicator. The current Tpetra implementation of this method does nothing.
This method is called in fillComplete().
Definition at line 3780 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Create a (or fetch a cached) column Map MultiVector.
| X_domainMap | [in] A domain Map Multivector. The returned MultiVector, if nonnull, will have the same number of columns as Y_domainMap. |
| force | [in] Force creating the MultiVector if it hasn't been created already. |
The force parameter is helpful when the domain Map and the column Map are the same (so that normally we wouldn't need the column Map MultiVector), but the following (for example) holds:
We don't test for the above in this method, because it depends on the specific kernel.
Definition at line 6394 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Create a (or fetch a cached) row Map MultiVector.
| Y_rangeMap | [in] A range Map Multivector. The returned MultiVector, if nonnull, will have the same number of columns as Y_rangeMap. |
| force | [in] Force creating the MultiVector if it hasn't been created already. |
The force parameter is helpful when the range Map and the row Map are the same (so that normally we wouldn't need the row Map MultiVector), but one of the following holds:
We don't test for the above in this method, because it depends on the specific kernel.
Definition at line 6457 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Special case of apply() for mode == Teuchos::NO_TRANS.
Definition at line 4119 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Special case of apply() for mode != Teuchos::NO_TRANS.
Definition at line 4287 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Constant view of all entries (including extra space) in the given row.
Unlike getGlobalRowView(), this method returns impl_scalar_type, not Scalar. This is because this method is not part of the public interface of CrsMatrix.
Definition at line 2467 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Nonconst view of all entries (including extra space) in the given row.
Unlike getGlobalRowView(), this method returns impl_scalar_type, not Scalar. This is because this method is not part of the public interface of CrsMatrix.
Definition at line 2509 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Fill data into the local matrix.
This method is only called in fillComplete(), and it is only called if the graph's structure is already fixed (that is, if the matrix does not own the graph).
Definition at line 1277 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Fill data into the local graph and matrix.
This method is only called in fillComplete(), and it is only called if the graph's structure is not already fixed (that is, if the matrix does own the graph).
Definition at line 836 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
protected |
Check that this object's state is sane; throw if it's not.
Definition at line 5220 of file Tpetra_KokkosRefactor_CrsMatrix_def.hpp.
|
pure virtualinherited |
Get a constant, nonpersisting, globally indexed view of the given row of the matrix.
The returned views of the column indices and values are not guaranteed to persist beyond the lifetime of this. Furthermore, some RowMatrix implementations allow changing the values, or the indices and values. Any such changes invalidate the returned views.
This method only gets the entries in the given row that are stored on the calling process. Note that if the matrix has an overlapping row Map, it is possible that the calling process does not store all the entries in that row.
isGloballyIndexed () && supportsRowViews () indices.size () == getNumEntriesInGlobalRow (GlobalRow)| GlobalRow | [in] Global index of the row. |
| Indices | [out] Global indices of the columns corresponding to values. |
| Values | [out] Matrix values. |
If GlobalRow does not belong to this node, then indices is set to null.
|
pure virtualinherited |
Get a constant, nonpersisting, locally indexed view of the given row of the matrix.
The returned views of the column indices and values are not guaranteed to persist beyond the lifetime of this. Furthermore, some RowMatrix implementations allow changing the values, or the indices and values. Any such changes invalidate the returned views.
This method only gets the entries in the given row that are stored on the calling process. Note that if the matrix has an overlapping row Map, it is possible that the calling process does not store all the entries in that row.
isLocallyIndexed () && supportsRowViews () indices.size () == getNumEntriesInGlobalRow (LocalRow)| LocalRow | [in] Local index of the row. |
| Indices | [out] Local indices of the columns corresponding to values. |
| Values | [out] Matrix values. |
If LocalRow does not belong to this node, then indices is set to null.
|
pure virtualinherited |
Get a copy of the diagonal entries, distributed by the row Map.
On input, the Vector's Map must be the same as the row Map of the matrix. (That is, this->getRowMap ()->isSameAs (* (diag.getMap ())) == true.)
On return, the entries of diag are filled with the diagonal entries of the matrix stored on this process. Note that if the row Map is overlapping, multiple processes may own the same diagonal element. You may combine these overlapping diagonal elements by doing an Export from the row Map Vector to a range Map Vector.
|
pure virtualinherited |
Scale the RowMatrix on the left with the given Vector x.
On return, for all entries i,j in the matrix,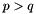 
.
|
pure virtualinherited |
Scale the RowMatrix on the right with the given Vector x.
On return, for all entries i,j in the matrix,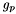 
.
|
mutableprotected |
Column Map MultiVector used in apply() and gaussSeidel().
This is a column Map MultiVector. It is used as the target of the forward mode Import operation (if necessary) in apply() and gaussSeidel(), and the source of the reverse mode Export operation (if necessary) in these methods. Both of these methods create this MultiVector on demand if needed, and reuse it (if possible) for subsequent calls.
This is declared mutable because the methods in question are const, yet want to cache the MultiVector for later use.
Definition at line 2921 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
mutableprotected |
Row Map MultiVector used in apply().
This is a row Map MultiVector. It is uses as the source of the forward mode Export operation (if necessary) in apply() and gaussSeidel(), and the target of the reverse mode Import operation (if necessary) in these methods. Both of these methods create this MultiVector on demand if needed, and reuse it (if possible) for subsequent calls.
This is declared mutable because the methods in question are const, yet want to cache the MultiVector for later use.
Definition at line 2935 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
protected |
The local sparse matrix.
Definition at line 3054 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
protected |
Status of the matrix's storage, when not in a fill-complete state.
The phrase "When not in a fill-complete state" is important. When the matrix is fill complete, it always uses 1-D "packed" storage. However, if the "Optimize Storage" parameter to fillComplete was false, the matrix may keep unpacked 1-D or 2-D storage around and resume it on the next resumeFill call.
Definition at line 3082 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
protected |
Whether the matrix is fill complete.
Definition at line 3085 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
protected |
Nonlocal data added using insertGlobalValues().
These data are cleared by globalAssemble(), once it finishes redistributing them to their owning processes.
For a given nonowned global row gRow which was given to insertGlobalValues() or sumIntoGlobalValues(), nonlocals_[gRow].first[k] is the column index of an inserted entry, and nonlocals_[gRow].second[k] is its value. Duplicate column indices for the same row index are allowed and will be summed during globalAssemble().
This used to be a map from GlobalOrdinal to (GlobalOrdinal, Scalar) pairs. This makes gcc issue a "note" about the ABI of structs containing std::complex members changing. CDash reports this as a warning, even though it's a "note," not a warning. However, I don't want it to show up, so I rearranged the map's value type to a pair of arrays, rather than an array of pairs.
Definition at line 3115 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
|
mutableprotected |
Cached Frobenius norm of the (global) matrix.
The value -1 means that the norm has not yet been computed, or that the values in the matrix may have changed and the norm must be recomputed.
Definition at line 3122 of file Tpetra_KokkosRefactor_CrsMatrix_decl.hpp.
1.8.6