Step Control Strategy for first-order time integration. More...

#include <Rythmos_FirstOrderErrorStepControlStrategy_decl.hpp>

Inheritance diagram for Rythmos::FirstOrderErrorStepControlStrategy< Scalar >:

Public Member Functions
void	initialize (const StepperBase< Scalar > &stepper)

Overridden from StepControlStrategyBase
void	setRequestedStepSize (const StepperBase< Scalar > &stepper, const Scalar &stepSize, const StepSizeType &stepSizeType)

void	nextStepSize (const StepperBase< Scalar > &stepper, Scalar stepSize, StepSizeType stepSizeType, int *order)

void	setCorrection (const StepperBase< Scalar > &stepper, const RCP< const Thyra::VectorBase< Scalar > > &soln, const RCP< const Thyra::VectorBase< Scalar > > &ee, int solveStatus)

bool	acceptStep (const StepperBase< Scalar > &stepper, Scalar *LETValue)

void	completeStep (const StepperBase< Scalar > &stepper)

AttemptedStepStatusFlag	rejectStep (const StepperBase< Scalar > &stepper)

StepControlStrategyState	getCurrentState ()

int	getMaxOrder () const

void	setStepControlData (const StepperBase< Scalar > &stepper)

bool	supportsCloning () const

RCP< StepControlStrategyBase < Scalar > >	cloneStepControlStrategyAlgorithm () const

Overridden from Teuchos::Describable
void	describe (Teuchos::FancyOStream &out, const Teuchos::EVerbosityLevel verbLevel) const

Overridden from ParameterListAcceptor
void	setParameterList (RCP< Teuchos::ParameterList > const &paramList)

RCP< Teuchos::ParameterList >	getNonconstParameterList ()

RCP< Teuchos::ParameterList >	unsetParameterList ()

RCP< const Teuchos::ParameterList >	getValidParameters () const

Detailed Description

template<class Scalar>
class Rythmos::FirstOrderErrorStepControlStrategy< Scalar >

Step Control Strategy for first-order time integration.

This step-control strategy assumes a first-order predictor (Forward Euler) for a first-order time integrator (Backward Euler) and tries to maintain a constant error based on relative and absolute tolerances by adjusting the step size. Although specifically built from Forward and Backward Euler, one could use this for other first-order schemes. See Grasho and Sani, "Incompressible Flow and the Finite Element Method", Volume One, p. 268.

Theory

To control the error through step-size selection, Forward Euler is used as a predictor

$x^P_n = x_{n-1} + \Delta t f(x_{n-1}, t_{n-1})$

with the local truncation error (LTE) of

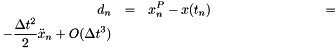
$\begin{eqnarray*} d_n &=& x^P_n - x(t_n) &=& -\frac{\Delta t^2}{2} \ddot{x}_n + O(\Delta t^3) \end{eqnarray*}$

Similarly for Backward Euler

$x_n = x_{n-1} + \Delta t f(x_n, t_n)$

with the local truncation error (LTE) of

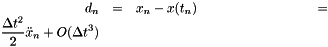
$\begin{eqnarray*} d_n &=& x_n - x(t_n) &=& \frac{\Delta t^2}{2} \ddot{x}_n + O(\Delta t^3) \end{eqnarray*}$

Using the Forward Euler as an estimate of the LTE for the Backward Euler, eliminating 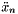$\ddot{x}_n$ , and forming 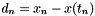$ d_n = x_n - x(t_n) $ in terms of 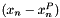$ (x_n - x^P_n) $ , we get

$d_n = x_n - x(t_n) = (x_n - x^P_n)/2$

which gives us an estimate of the LTE, 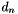$ d_n $ in term of the difference between the Backward Euler solution, 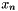$ x_n $ , and the predicted Forward Euler solution, $ x^P_n $ .

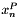To select the next step size, we would like the LTE to be meet a user-supplied tolerance,

$d_{n+1} \leq \epsilon_r ||x_n|| + \epsilon_a$

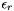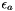where $\epsilon_r$ and $\epsilon_a$ are the relative and absolute tolerances, and 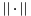$||\cdot||$ is the norm. Normalizing this with respect to the current step, which allows us the relate the current step size to the next step size, and using the LTE, we find

$\frac{d_{n+1}}{d_n} = \frac{\epsilon_r ||x_n|| + \epsilon_a}{d_n} = \frac{\Delta t^2_{n+1} \ddot{x}_{n+1}}{\Delta t^2_n \ddot{x}_n} = \left(\frac{\Delta t_{n+1}}{\Delta t_n}\right)^2 + O(\Delta t)$

leading to the value for the next step size

$\Delta t_{n+1} = \Delta t_n \left(\frac{\epsilon_r ||x_n|| + \epsilon_a}{d_n}\right)^{1/2}$

Definition at line 101 of file Rythmos_FirstOrderErrorStepControlStrategy_decl.hpp.

Member Function Documentation

template<class Scalar >

void Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::setRequestedStepSize	(	const StepperBase< Scalar > &	stepper,
		const Scalar &	stepSize,
		const StepSizeType &	stepSizeType
	)

virtual

Implements Rythmos::StepControlStrategyBase< Scalar >.

Definition at line 201 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

void Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::nextStepSize	(	const StepperBase< Scalar > &	stepper,
		Scalar *	stepSize,
		StepSizeType *	stepSizeType,
		int *	order
	)

virtual

Implements Rythmos::StepControlStrategyBase< Scalar >.

Definition at line 236 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

void Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::setCorrection	(	const StepperBase< Scalar > &	stepper,
		const RCP< const Thyra::VectorBase< Scalar > > &	soln,
		const RCP< const Thyra::VectorBase< Scalar > > &	ee,
		int	solveStatus
	)

virtual

Implements Rythmos::StepControlStrategyBase< Scalar >.

Definition at line 267 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

bool Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::acceptStep	(	const StepperBase< Scalar > &	stepper,
		Scalar *	LETValue
	)

virtual

Implements Rythmos::StepControlStrategyBase< Scalar >.

Definition at line 283 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

void Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::completeStep ( const StepperBase< Scalar > & stepper )

virtual

Implements Rythmos::StepControlStrategyBase< Scalar >.

Definition at line 384 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

AttemptedStepStatusFlag Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::rejectStep ( const StepperBase< Scalar > & stepper )

virtual

Implements Rythmos::StepControlStrategyBase< Scalar >.

Definition at line 331 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

StepControlStrategyState Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::getCurrentState ( )

virtual

Implements Rythmos::StepControlStrategyBase< Scalar >.

Definition at line 150 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

int Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::getMaxOrder ( ) const

virtual

Implements Rythmos::StepControlStrategyBase< Scalar >.

Definition at line 607 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

void Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::setStepControlData ( const StepperBase< Scalar > & stepper )

virtual

Implements Rythmos::StepControlStrategyBase< Scalar >.

Definition at line 579 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

bool Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::supportsCloning ( ) const

virtual

Reimplemented from Rythmos::StepControlStrategyBase< Scalar >.

Definition at line 586 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

RCP< StepControlStrategyBase< Scalar > > Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::cloneStepControlStrategyAlgorithm ( ) const

virtual

Reimplemented from Rythmos::StepControlStrategyBase< Scalar >.

Definition at line 594 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

void Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::describe	(	Teuchos::FancyOStream &	out,
		const Teuchos::EVerbosityLevel	verbLevel
	)		const

Definition at line 418 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

void Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::setParameterList ( RCP< Teuchos::ParameterList > const & paramList )

Definition at line 440 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

RCP< Teuchos::ParameterList > Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::getNonconstParameterList ( )

Definition at line 573 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

RCP< Teuchos::ParameterList > Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::unsetParameterList ( )

Definition at line 564 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

RCP< const Teuchos::ParameterList > Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::getValidParameters ( ) const

Definition at line 526 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

template<class Scalar >

void Rythmos::FirstOrderErrorStepControlStrategy< Scalar >::initialize ( const StepperBase< Scalar > & stepper )

virtual

Implements Rythmos::StepControlStrategyBase< Scalar >.

Definition at line 173 of file Rythmos_FirstOrderErrorStepControlStrategy_def.hpp.

The documentation for this class was generated from the following files:

Public Member Functions

Overridden from StepControlStrategyBase

Overridden from Teuchos::Describable

Overridden from ParameterListAcceptor

Detailed Description

template<class Scalar> class Rythmos::FirstOrderErrorStepControlStrategy< Scalar >

Theory

Member Function Documentation

template<class Scalar>
class Rythmos::FirstOrderErrorStepControlStrategy< Scalar >