|
Anasazi
Version of the Day
|
|
Anasazi
Version of the Day
|
Anasazi's templated, static class providing utilities for the solvers. More...
#include <AnasaziSolverUtils.hpp>
Public Member Functions | |
Constructor/Destructor | |
| SolverUtils () | |
| Constructor. More... | |
| virtual | ~SolverUtils () |
| Destructor. More... | |
Static Public Member Functions | |
Sorting Methods | |
| static void | permuteVectors (const int n, const std::vector< int > &perm, MV &Q, std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > *resids=0) |
Permute the vectors in a multivector according to the permutation vector perm, and optionally the residual vector resids. More... | |
| static void | permuteVectors (const std::vector< int > &perm, Teuchos::SerialDenseMatrix< int, ScalarType > &Q) |
Permute the columns of a Teuchos::SerialDenseMatrix according to the permutation vector perm. More... | |
Basis update methods | |
| static void | applyHouse (int k, MV &V, const Teuchos::SerialDenseMatrix< int, ScalarType > &H, const std::vector< ScalarType > &tau, Teuchos::RCP< MV > workMV=Teuchos::null) |
Apply a sequence of Householder reflectors (from GEQRF) to a multivector, using minimal workspace. More... | |
Eigensolver Projection Methods | |
| static int | directSolver (int size, const Teuchos::SerialDenseMatrix< int, ScalarType > &KK, Teuchos::RCP< const Teuchos::SerialDenseMatrix< int, ScalarType > > MM, Teuchos::SerialDenseMatrix< int, ScalarType > &EV, std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > &theta, int &nev, int esType=0) |
Routine for computing the first NEV generalized eigenpairs of the Hermitian pencil (KK, MM) More... | |
Sanity Checking Methods | |
| static Teuchos::ScalarTraits < ScalarType >::magnitudeType | errorEquality (const MV &X, const MV &MX, Teuchos::RCP< const OP > M=Teuchos::null) |
Return the maximum coefficient of the matrix 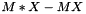 scaled by the maximum coefficient of scaled by the maximum coefficient of MX. More... | |
Anasazi's templated, static class providing utilities for the solvers.
This class provides concrete, templated implementations of utilities necessary for the solvers. These utilities include sorting, orthogonalization, projecting/solving local eigensystems, and sanity checking. These are internal utilties, so the user should not alter this class.
Definition at line 42 of file AnasaziSolverUtils.hpp.
| Anasazi::SolverUtils< ScalarType, MV, OP >::SolverUtils | ( | ) |
Constructor.
Definition at line 164 of file AnasaziSolverUtils.hpp.
|
inlinevirtual |
Destructor.
Definition at line 55 of file AnasaziSolverUtils.hpp.
|
static |
Permute the vectors in a multivector according to the permutation vector perm, and optionally the residual vector resids.
Definition at line 176 of file AnasaziSolverUtils.hpp.
|
static |
Permute the columns of a Teuchos::SerialDenseMatrix according to the permutation vector perm.
Definition at line 240 of file AnasaziSolverUtils.hpp.
|
static |
Apply a sequence of Householder reflectors (from GEQRF) to a multivector, using minimal workspace.
| k | [in] the number of Householder reflectors composing the product |
| V | [in/out] the multivector to be modified, with 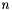 columns columns |
| H | [in] a  matrix containing the encoded Householder vectors, as returned from matrix containing the encoded Householder vectors, as returned from GEQRF (see below) |
| tau | [in] the 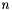 coefficients for the Householder reflects, as returned from coefficients for the Householder reflects, as returned from GEQRF |
| workMV | [work] (optional) a multivector used for workspace. it need contain only a single vector; it if contains more, only the first vector will be modified. |
This routine applies a sequence of Householder reflectors, 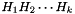 , to a multivector
, to a multivector 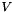 . The reflectors are applied individually, as rank-one updates to the multivector. The benefit of this is that the only required workspace is a one-column multivector. This workspace can be provided by the user. If it is not, it will be allocated locally on each call to applyHouse.
. The reflectors are applied individually, as rank-one updates to the multivector. The benefit of this is that the only required workspace is a one-column multivector. This workspace can be provided by the user. If it is not, it will be allocated locally on each call to applyHouse.
Each 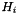 (
(  ) has the form
) has the form
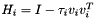
where 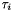 is a scalar and
is a scalar and 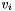 is a vector with
is a vector with 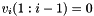 and
and 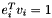 ;
; 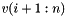 is stored below
is stored below H(i,i) and 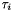 in
in tau[i-1]. (Note: zero-based indexing used for data structures H and tau, while one-based indexing used for mathematic object 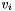 ).
).
If the multivector is 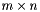 and we apply
and we apply  Householder reflectors, the total cost of the method is
Householder reflectors, the total cost of the method is 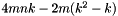 flops. For
flops. For 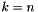 , this becomes
, this becomes 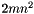 , the same as for a matrix-matrix multiplication by the accumulated Householder reflectors.
, the same as for a matrix-matrix multiplication by the accumulated Householder reflectors.
Definition at line 268 of file AnasaziSolverUtils.hpp.
|
static |
Routine for computing the first NEV generalized eigenpairs of the Hermitian pencil (KK, MM)
@param size [in] Dimension of the eigenproblem (KK, MM)
@param KK [in] Hermitian "stiffness" matrix
@param MM [in] Hermitian positive-definite "mass" matrix
@param EV [in] Dense matrix to store the nev eigenvectors
@param theta [in] Array to store the eigenvalues (Size = nev )
@param nev [in/out] Number of the smallest eigenvalues requested (in) / computed (out)
@param esType [in] Flag to select the algorithm
<ul>
<li> esType = 0 (default) Uses LAPACK routine (Cholesky factorization of MM)
with deflation of MM to get orthonormality of
eigenvectors ( \form#90)
<li> esType = 1 Uses LAPACK routine (Cholesky factorization of MM)
(no check of orthonormality)
<li> esType = 10 Uses LAPACK routine for simple eigenproblem on KK
(MM is not referenced in this case)
</ul>
\note The code accesses only the upper triangular part of KK and MM.
\return Integer \c info on the status of the computation
Return the integer info on the status of the computation
Definition at line 337 of file AnasaziSolverUtils.hpp.
|
static |
Return the maximum coefficient of the matrix 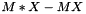 scaled by the maximum coefficient of
scaled by the maximum coefficient of MX.
M is not specified, the identity is used. Definition at line 616 of file AnasaziSolverUtils.hpp.
 1.8.5
1.8.5