An implementation of the Anasazi::MatOrthoManager that performs orthogonalization using the SVQB iterative orthogonalization technique described by Stathapoulos and Wu. This orthogonalization routine, while not returning the upper triangular factors of the popular Gram-Schmidt method, has a communication cost (measured in number of communication calls) that is independent of the number of columns in the basis. More...

#include <AnasaziSVQBOrthoManager.hpp>

Inheritance diagram for Anasazi::SVQBOrthoManager< ScalarType, MV, OP >:

Public Member Functions
Constructor/Destructor
	SVQBOrthoManager (Teuchos::RCP< const OP > Op=Teuchos::null, bool debug=false)
	Constructor specifying re-orthogonalization tolerance. More...

	~SVQBOrthoManager ()
	Destructor. More...

Methods implementing Anasazi::MatOrthoManager
void	projectMat (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< MV > MX=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MQ=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const
	Given a list of mutually orthogonal and internally orthonormal bases `Q`, this method projects a multivector `X` onto the space orthogonal to the individual `Q[i]`, optionally returning the coefficients of `X` for the individual `Q[i]`. All of this is done with respect to the inner product innerProd(). More...

int	normalizeMat (MV &X, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null, Teuchos::RCP< MV > MX=Teuchos::null) const
	This method takes a multivector `X` and attempts to compute an orthonormal basis for 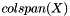, with respect to innerProd(). More...

int	projectAndNormalizeMat (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null, Teuchos::RCP< MV > MX=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MQ=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const
	Given a set of bases `Q[i]` and a multivector `X`, this method computes an orthonormal basis for $colspan(X) - \sum_i colspan(Q[i])$ . More...

Error methods
Teuchos::ScalarTraits < ScalarType >::magnitudeType	orthonormErrorMat (const MV &X, Teuchos::RCP< const MV > MX=Teuchos::null) const
	This method computes the error in orthonormality of a multivector, measured as the Frobenius norm of the difference `innerProd(X,Y) - I`. The method has the option of exploiting a caller-provided `MX`. More...

Teuchos::ScalarTraits < ScalarType >::magnitudeType	orthogErrorMat (const MV &X, const MV &Y, Teuchos::RCP< const MV > MX=Teuchos::null, Teuchos::RCP< const MV > MY=Teuchos::null) const
	This method computes the error in orthogonality of two multivectors, measured as the Frobenius norm of `innerProd(X,Y)`. The method has the option of exploiting a caller-provided `MX`. More...

Public Member Functions inherited from Anasazi::MatOrthoManager< ScalarType, MV, OP >
	MatOrthoManager (Teuchos::RCP< const OP > Op=Teuchos::null)
	Default constructor. More...

virtual	~MatOrthoManager ()
	Destructor. More...

virtual void	setOp (Teuchos::RCP< const OP > Op)
	Set operator used for inner product. More...

virtual Teuchos::RCP< const OP >	getOp () const
	Get operator used for inner product. More...

int	getOpCounter () const
	Retrieve operator counter. More...

void	resetOpCounter ()
	Reset the operator counter to zero. More...

void	innerProdMat (const MV &X, const MV &Y, Teuchos::SerialDenseMatrix< int, ScalarType > &Z, Teuchos::RCP< const MV > MX=Teuchos::null, Teuchos::RCP< const MV > MY=Teuchos::null) const
	Provides a matrix-based inner product. More...

void	normMat (const MV &X, std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > &normvec, Teuchos::RCP< const MV > MX=Teuchos::null) const
	Provides the norm induced by the matrix-based inner product. More...

void	innerProd (const MV &X, const MV &Y, Teuchos::SerialDenseMatrix< int, ScalarType > &Z) const
	Implements the interface OrthoManager::innerProd(). More...

void	norm (const MV &X, std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > &normvec) const
	Implements the interface OrthoManager::norm(). More...

void	project (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null))) const
	Implements the interface OrthoManager::project(). More...

int	normalize (MV &X, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null) const
	Implements the interface OrthoManager::normalize(). More...

int	projectAndNormalize (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null) const
	Implements the interface OrthoManager::projectAndNormalize(). More...

Teuchos::ScalarTraits < ScalarType >::magnitudeType	orthonormError (const MV &X) const
	Implements the interface OrthoManager::orthonormError(). More...

Teuchos::ScalarTraits < ScalarType >::magnitudeType	orthogError (const MV &X1, const MV &X2) const
	Implements the interface OrthoManager::orthogError(). More...

Public Member Functions inherited from Anasazi::OrthoManager< ScalarType, MV >
	OrthoManager ()
	Default constructor. More...

virtual	~OrthoManager ()
	Destructor. More...

Detailed Description

template<class ScalarType, class MV, class OP>
class Anasazi::SVQBOrthoManager< ScalarType, MV, OP >

An implementation of the Anasazi::MatOrthoManager that performs orthogonalization using the SVQB iterative orthogonalization technique described by Stathapoulos and Wu. This orthogonalization routine, while not returning the upper triangular factors of the popular Gram-Schmidt method, has a communication cost (measured in number of communication calls) that is independent of the number of columns in the basis.

Author: Chris Baker, Ulrich Hetmaniuk, Rich Lehoucq, and Heidi Thornquist

Definition at line 37 of file AnasaziSVQBOrthoManager.hpp.

Constructor & Destructor Documentation

template<class ScalarType , class MV , class OP >

Anasazi::SVQBOrthoManager< ScalarType, MV, OP >::SVQBOrthoManager	(	Teuchos::RCP< const OP >	Op = `Teuchos::null`,
		bool	debug = `false`
	)

Constructor specifying re-orthogonalization tolerance.

Definition at line 271 of file AnasaziSVQBOrthoManager.hpp.

template<class ScalarType , class MV , class OP >

Anasazi::SVQBOrthoManager< ScalarType, MV, OP >::~SVQBOrthoManager ( )

inline

Destructor.

Definition at line 57 of file AnasaziSVQBOrthoManager.hpp.

Member Function Documentation

template<class ScalarType , class MV , class OP >

void Anasazi::SVQBOrthoManager< ScalarType, MV, OP >::projectMat	(	MV &	X,
		Teuchos::Array< Teuchos::RCP< const MV > >	Q,
		Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > >	C = `Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix<int,ScalarType> >(Teuchos::null))`,
		Teuchos::RCP< MV >	MX = `Teuchos::null`,
		Teuchos::Array< Teuchos::RCP< const MV > >	MQ = `Teuchos::tuple(Teuchos::RCP<const MV>(Teuchos::null))`
	)		const

virtual

Given a list of mutually orthogonal and internally orthonormal bases Q, this method projects a multivector X onto the space orthogonal to the individual Q[i], optionally returning the coefficients of X for the individual Q[i]. All of this is done with respect to the inner product innerProd().

After calling this routine, X will be orthogonal to each of the Q[i].

Parameters

X	[in/out] The multivector to be modified. On output, the columns of `X` will be orthogonal to each `Q[i]`, satisfying $X_{out} = X_{in} - \sum_i Q[i] \langle Q[i], X_{in} \rangle$
MX	[in/out] The image of `X` under the inner product operator `Op`. If 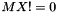: On input, this is expected to be consistent with `Op` X. On output, this is updated consistent with updates to `X`. If 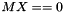or : `MX` is not referenced.
C	[out] The coefficients of `X` in the bases `Q[i]`. If `C[i]` is a non-null pointer and `C[i]` matches the dimensions of `X` and `Q[i]`, then the coefficients computed during the orthogonalization routine will be stored in the matrix `C[i]`, similar to calling innerProd( Q[i], X, C[i] ); If `C[i]` points to a Teuchos::SerialDenseMatrix with size inconsistent with `X` and `Q[i]`, then a std::invalid_argument exception will be thrown. Otherwise, if `C.size() < i` or `C[i]` is a null pointer, the caller will not have access to the computed coefficients.
Q	[in] A list of multivector bases specifying the subspaces to be orthogonalized against, satisfying $\langle Q[i], Q[j] \rangle = I \quad\textrm{if}\quad i=j$ and $\langle Q[i], Q[j] \rangle = 0 \quad\textrm{if}\quad i \neq j\ .$

Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.

Definition at line 318 of file AnasaziSVQBOrthoManager.hpp.

template<class ScalarType , class MV , class OP >

int Anasazi::SVQBOrthoManager< ScalarType, MV, OP >::normalizeMat	(	MV &	X,
		Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >	B = `Teuchos::null`,
		Teuchos::RCP< MV >	MX = `Teuchos::null`
	)		const

virtual

This method takes a multivector X and attempts to compute an orthonormal basis for 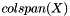$colspan(X)$ , with respect to innerProd().

This method does not compute an upper triangular coefficient matrix B.

This routine returns an integer rank stating the rank of the computed basis. If X does not have full rank and the normalize() routine does not attempt to augment the subspace, then rank may be smaller than the number of columns in X. In this case, only the first rank columns of output X and first rank rows of B will be valid.

The method attempts to find a basis with dimension equal to the number of columns in X. It does this by augmenting linearly dependent vectors in X with random directions. A finite number of these attempts will be made; therefore, it is possible that the dimension of the computed basis is less than the number of vectors in X.

Parameters

X

[in/out] The multivector to be modified.
On output, the first rank columns of X satisfy

$\langle X[i], X[j] \rangle = \delta_{ij}\ .$

Also,

$X_{in}(1:m,1:n) = X_{out}(1:m,1:rank) B(1:rank,1:n)$

where m is the number of rows in X and n is the number of columns in X.

MX [in/out] The image of X under the inner product operator Op. If 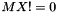: On input, this is expected to be consistent with Op X. On output, this is updated consistent with updates to X. If 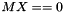or : MX is not referenced.

B

[out] The coefficients of the original X with respect to the computed basis. If B is a non-null pointer and B matches the dimensions of B, then the coefficients computed during the orthogonalization routine will be stored in B, similar to calling

innerProd( Xout, Xin, B );

If B points to a Teuchos::SerialDenseMatrix with size inconsistent with X, then a std::invalid_argument exception will be thrown. Otherwise, if B is null, the caller will not have access to the computed coefficients. This matrix is not necessarily triangular (as in a QR factorization); see the documentation of specific orthogonalization managers.
In general, B has no non-zero structure.

Returns: Rank of the basis computed by this method, less than or equal to the number of columns in X. This specifies how many columns in the returned X and rows in the returned B are valid.

Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.

Definition at line 333 of file AnasaziSVQBOrthoManager.hpp.

template<class ScalarType , class MV , class OP >

int Anasazi::SVQBOrthoManager< ScalarType, MV, OP >::projectAndNormalizeMat	(	MV &	X,
		Teuchos::Array< Teuchos::RCP< const MV > >	Q,
		Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > >	C = `Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix<int,ScalarType> >(Teuchos::null))`,
		Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >	B = `Teuchos::null`,
		Teuchos::RCP< MV >	MX = `Teuchos::null`,
		Teuchos::Array< Teuchos::RCP< const MV > >	MQ = `Teuchos::tuple(Teuchos::RCP<const MV>(Teuchos::null))`
	)		const

virtual

Given a set of bases Q[i] and a multivector X, this method computes an orthonormal basis for $colspan(X) - \sum_i colspan(Q[i])$ .

This routine returns an integer rank stating the rank of the computed basis. If the subspace $colspan(X) - \sum_i colspan(Q[i])$ does not have dimension as large as the number of columns of X and the orthogonalization manager doe not attempt to augment the subspace, then rank may be smaller than the number of columns of X. In this case, only the first rank columns of output X and first rank rows of B will be valid.

The method attempts to find a basis with dimension the same as the number of columns in X. It does this by augmenting linearly dependent vectors with random directions. A finite number of these attempts will be made; therefore, it is possible that the dimension of the computed basis is less than the number of vectors in X.

Parameters

X	[in/out] The multivector to be modified. On output, the first `rank` columns of `X` satisfy $\langle X[i], X[j] \rangle = \delta_{ij} \quad \textrm{and} \quad \langle X, Q[i] \rangle = 0\ .$ Also, $X_{in}(1:m,1:n) = X_{out}(1:m,1:rank) B(1:rank,1:n) + \sum_i Q[i] C[i]$ where `m` is the number of rows in `X` and `n` is the number of columns in `X`.
MX	[in/out] The image of `X` under the inner product operator `Op`. If 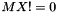: On input, this is expected to be consistent with `Op` X. On output, this is updated consistent with updates to `X`. If 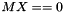or : `MX` is not referenced.
C	[out] The coefficients of `X` in the `Q[i]`. If `C[i]` is a non-null pointer and `C[i]` matches the dimensions of `X` and `Q[i]`, then the coefficients computed during the orthogonalization routine will be stored in the matrix `C[i]`, similar to calling innerProd( Q[i], X, C[i] ); If `C[i]` points to a Teuchos::SerialDenseMatrix with size inconsistent with `X` and `Q[i]`, then a std::invalid_argument exception will be thrown. Otherwise, if `C.size() < i` or `C[i]` is a null pointer, the caller will not have access to the computed coefficients.
B	[out] The coefficients of the original `X` with respect to the computed basis. If `B` is a non-null pointer and `B` matches the dimensions of `B`, then the coefficients computed during the orthogonalization routine will be stored in `B`, similar to calling innerProd( Xout, Xin, B ); If `B` points to a Teuchos::SerialDenseMatrix with size inconsistent with `X`, then a std::invalid_argument exception will be thrown. Otherwise, if `B` is null, the caller will not have access to the computed coefficients. This matrix is not necessarily triangular (as in a QR factorization); see the documentation of specific orthogonalization managers. In general, `B` has no non-zero structure.
Q	[in] A list of multivector bases specifying the subspaces to be orthogonalized against, satisfying $\langle Q[i], Q[j] \rangle = I \quad\textrm{if}\quad i=j$ and $\langle Q[i], Q[j] \rangle = 0 \quad\textrm{if}\quad i \neq j\ .$

Returns: Rank of the basis computed by this method, less than or equal to the number of columns in X. This specifies how many columns in the returned X and rows in the returned B are valid.

Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.

Definition at line 347 of file AnasaziSVQBOrthoManager.hpp.

template<class ScalarType , class MV , class OP >

Teuchos::ScalarTraits< ScalarType >::magnitudeType Anasazi::SVQBOrthoManager< ScalarType, MV, OP >::orthonormErrorMat	(	const MV &	X,
		Teuchos::RCP< const MV >	MX = `Teuchos::null`
	)		const

virtual

This method computes the error in orthonormality of a multivector, measured as the Frobenius norm of the difference innerProd(X,Y) - I. The method has the option of exploiting a caller-provided MX.

Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.

Definition at line 286 of file AnasaziSVQBOrthoManager.hpp.

template<class ScalarType , class MV , class OP >

Teuchos::ScalarTraits< ScalarType >::magnitudeType Anasazi::SVQBOrthoManager< ScalarType, MV, OP >::orthogErrorMat	(	const MV &	X,
		const MV &	Y,
		Teuchos::RCP< const MV >	MX = `Teuchos::null`,
		Teuchos::RCP< const MV >	MY = `Teuchos::null`
	)		const

virtual

This method computes the error in orthogonality of two multivectors, measured as the Frobenius norm of innerProd(X,Y). The method has the option of exploiting a caller-provided MX.

Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.

Definition at line 301 of file AnasaziSVQBOrthoManager.hpp.

The documentation for this class was generated from the following file:

AnasaziSVQBOrthoManager.hpp

Public Member Functions

Detailed Description

template<class ScalarType, class MV, class OP> class Anasazi::SVQBOrthoManager< ScalarType, MV, OP >

Constructor & Destructor Documentation

Member Function Documentation

template<class ScalarType, class MV, class OP>
class Anasazi::SVQBOrthoManager< ScalarType, MV, OP >