Anasazi  Version of the Day
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Groups Pages
Public Member Functions | List of all members
Anasazi::TsqrOrthoManager< Scalar, MV > Class Template Reference

TSQR-based OrthoManager subclass. More...

#include <AnasaziTsqrOrthoManager.hpp>

Inheritance diagram for Anasazi::TsqrOrthoManager< Scalar, MV >:
Anasazi::OrthoManager< Scalar, MV > Anasazi::OutOfPlaceNormalizerMixin< Scalar, MV > Teuchos::ParameterListAcceptor

Public Member Functions

Teuchos::RCP< const
Teuchos::ParameterList > 		getValidParameters () const
 Default valid parameter list. More...
 
Teuchos::RCP< const
Teuchos::ParameterList > 		getFastParameters () const
 Get "fast" parameters for TsqrOrthoManager. More...
 
 TsqrOrthoManager (const Teuchos::RCP< Teuchos::ParameterList > &params, const std::string &label="Anasazi")
 Constructor (that sets user-specified parameters). More...
 
 TsqrOrthoManager (const std::string &label)
 Constructor (that sets default parameters). More...
 
virtual ~TsqrOrthoManager ()
 Destructor, declared virtual for safe inheritance. More...
 
void innerProd (const MV &X, const MV &Y, mat_type &Z) const
 Provides the inner product defining the orthogonality concepts. More...
 
void project (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, Scalar > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, Scalar > >(Teuchos::null))) const
 Given a list of mutually orthogonal and internally orthonormal bases Q, this method projects a multivector X onto the space orthogonal to the individual Q[i], optionally returning the coefficients of X for the individual Q[i]. All of this is done with respect to the inner product innerProd(). More...
 
int projectAndNormalize (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, Scalar > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, Scalar > >(Teuchos::null)), Teuchos::RCP< Teuchos::SerialDenseMatrix< int, Scalar > > B=Teuchos::null) const
 Given a set of bases Q[i] and a multivector X, this method computes an orthonormal basis for $ colspan(X) - \sum_i colspan(Q[i])$. More...
 
int normalizeOutOfPlace (MV &X, MV &Q, mat_ptr B) const
 Normalize X into Q*B, overwriting X with invalid values. More...
 
int projectAndNormalizeOutOfPlace (MV &X_in, MV &X_out, Teuchos::Array< mat_ptr > C, mat_ptr B, Teuchos::ArrayView< Teuchos::RCP< const MV > > Q) const
 Project and normalize X_in into X_out; overwrite X_in. More...
 
magnitude_type orthonormError (const MV &X) const
 This method computes the error in orthonormality of a multivector. More...
 
magnitude_type orthogError (const MV &X1, const MV &X2) const
 This method computes the error in orthogonality of two multivectors. More...
 
- Public Member Functions inherited from Anasazi::OrthoManager< Scalar, MV >
 OrthoManager ()
 Default constructor. More...
 
virtual ~OrthoManager ()
 Destructor. More...
 
virtual void norm (const MV &X, std::vector< typename Teuchos::ScalarTraits< Scalar >::magnitudeType > &normvec) const =0
 Provides the norm induced by innerProd(). More...
 
virtual int normalize (MV &X, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, Scalar > > B=Teuchos::null) const =0
 This method takes a multivector X and attempts to compute a basis for 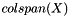$ colspan(X)$. This basis is orthonormal with respect to innerProd(). More...
 
- Public Member Functions inherited from Anasazi::OutOfPlaceNormalizerMixin< Scalar, MV >
virtual ~OutOfPlaceNormalizerMixin ()
 Trivial virtual destructor, to silence compiler warnings. More...
 

Additional Inherited Members

- Public Types inherited from Anasazi::OutOfPlaceNormalizerMixin< Scalar, MV >
typedef MV multivector_type
 Multivector type with which this class was specialized. More...
 

Detailed Description

template<class Scalar, class MV>
class Anasazi::TsqrOrthoManager< Scalar, MV >

TSQR-based OrthoManager subclass.

Author
Mark Hoemmen

Subclass of OrthoManager, implemented using TsqrOrthoManagerImpl (TSQR + Block Gram-Schmidt).

Definition at line 134 of file AnasaziTsqrOrthoManager.hpp.

Constructor & Destructor Documentation

template<class Scalar , class MV >
Anasazi::TsqrOrthoManager< Scalar, MV >::TsqrOrthoManager ( const Teuchos::RCP< Teuchos::ParameterList > &  params,
const std::string &  label = "Anasazi" 
)
inline

Constructor (that sets user-specified parameters).

Parameters
params[in/out] Configuration parameters, both for this orthogonalization manager, and for TSQR itself (as the "TsqrImpl" sublist). This can be null, in which case default parameters will be set for now; you can always call setParameterList() later to change these.
label[in] Label for timers. This only matters if the compile-time option for enabling timers is set.

Call getValidParameters() for default parameters and their documentation, including TSQR implementation parameters. Call getFastParameters() to get documented parameters for faster computation, possibly at the expense of accuracy and robustness.

Definition at line 200 of file AnasaziTsqrOrthoManager.hpp.

template<class Scalar , class MV >
Anasazi::TsqrOrthoManager< Scalar, MV >::TsqrOrthoManager ( const std::string &  label)
inline

Constructor (that sets default parameters).

Parameters
label[in] Label for timers. This only matters if the compile-time option for enabling timers is set.

Definition at line 209 of file AnasaziTsqrOrthoManager.hpp.

template<class Scalar , class MV >
virtual Anasazi::TsqrOrthoManager< Scalar, MV >::~TsqrOrthoManager ( )
inlinevirtual

Destructor, declared virtual for safe inheritance.

Definition at line 214 of file AnasaziTsqrOrthoManager.hpp.

Member Function Documentation

template<class Scalar , class MV >
Teuchos::RCP<const Teuchos::ParameterList> Anasazi::TsqrOrthoManager< Scalar, MV >::getValidParameters ( ) const
inlinevirtual

Default valid parameter list.

Get a (pointer to a) default list of parameters for configuring a TsqrOrthoManager instance.

Note
TSQR implementation configuration options are stored under "TsqrImpl" as a sublist.

Reimplemented from Teuchos::ParameterListAcceptor.

Definition at line 167 of file AnasaziTsqrOrthoManager.hpp.

template<class Scalar , class MV >
Teuchos::RCP<const Teuchos::ParameterList> Anasazi::TsqrOrthoManager< Scalar, MV >::getFastParameters ( ) const
inline

Get "fast" parameters for TsqrOrthoManager.

Get a (pointer to a) list of parameters for configuring a TsqrOrthoManager instance for maximum speed, at the cost of accuracy (no block reorthogonalization) and robustness to rank deficiency (no randomization of the null space basis).

Note
TSQR implementation configuration options are stored under "TsqrImpl" as a sublist.

Definition at line 180 of file AnasaziTsqrOrthoManager.hpp.

template<class Scalar , class MV >
void Anasazi::TsqrOrthoManager< Scalar, MV >::innerProd ( const MV &  X,
const MV &  Y,
mat_type &  Z 
) const
inlinevirtual

Provides the inner product defining the orthogonality concepts.

All concepts of orthogonality discussed in this class are defined with respect to this inner product.

Note
This is potentially different from MultiVecTraits::MvTransMv(). For example, it is customary in many eigensolvers to exploit a mass matrix M for the inner product: 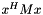$ x^HMx$.
Parameters
Z[out] Z(i,j) contains the inner product of X[i] and Y[i]:

\[ Z(i,j) = \langle X[i], Y[i] \rangle \]

Implements Anasazi::OrthoManager< Scalar, MV >.

Definition at line 216 of file AnasaziTsqrOrthoManager.hpp.

template<class Scalar , class MV >
void Anasazi::TsqrOrthoManager< Scalar, MV >::project ( MV &  X,
Teuchos::Array< Teuchos::RCP< const MV > >  Q,
Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, Scalar > > >  C = Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix<int,Scalar> >(Teuchos::null)) 
) const
inlinevirtual

Given a list of mutually orthogonal and internally orthonormal bases Q, this method projects a multivector X onto the space orthogonal to the individual Q[i], optionally returning the coefficients of X for the individual Q[i]. All of this is done with respect to the inner product innerProd().

After calling this routine, X will be orthogonal to each of the Q[i].

Parameters
X[in/out] The multivector to be modified.
On output, the columns of X will be orthogonal to each Q[i], satisfying

\[ \langle Q[i], X_{out} \rangle = 0 \]

Also,

\[ X_{out} = X_{in} - \sum_i Q[i] \langle Q[i], X_{in} \rangle \]

Q[in] A list of multivector bases specifying the subspaces to be orthogonalized against, satisfying

\[ \langle Q[i], Q[j] \rangle = I \quad\textrm{if}\quad i=j \]

and

\[ \langle Q[i], Q[j] \rangle = 0 \quad\textrm{if}\quad i \neq j\ . \]

C[out] The coefficients of X in the bases Q[i]. If C[i] is a non-null pointer and C[i] matches the dimensions of X and Q[i], then the coefficients computed during the orthogonalization routine will be stored in the matrix C[i], similar to calling
innerProd( Q[i], X, C[i] );
If C[i] points to a Teuchos::SerialDenseMatrix with size inconsistent with X and Q[i], then a std::invalid_argument exception will be thrown.
Otherwise, if C.size() < i or C[i] is a null pointer, the caller will not have access to the computed coefficients.

Implements Anasazi::OrthoManager< Scalar, MV >.

Definition at line 225 of file AnasaziTsqrOrthoManager.hpp.

template<class Scalar , class MV >
int Anasazi::TsqrOrthoManager< Scalar, MV >::projectAndNormalize ( MV &  X,
Teuchos::Array< Teuchos::RCP< const MV > >  Q,
Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, Scalar > > >  C = Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix<int,Scalar> >(Teuchos::null)),
Teuchos::RCP< Teuchos::SerialDenseMatrix< int, Scalar > >  B = Teuchos::null 
) const
inlinevirtual

Given a set of bases Q[i] and a multivector X, this method computes an orthonormal basis for $ colspan(X) - \sum_i colspan(Q[i])$.

This routine returns an integer rank stating the rank of the computed basis. If the subspace $ colspan(X) - \sum_i colspan(Q[i])$ does not have dimension as large as the number of columns of X and the orthogonalization manager does not attempt to augment the subspace, then rank may be smaller than the number of columns of X. In this case, only the first rank columns of output X and first rank rows of B will be valid.

Note
This routine guarantees both the orthogonality of the returned basis against the Q[i] as well as the orthonormality of the returned basis. Therefore, this method is not necessarily equivalent to calling project() followed by a call to normalize(); see the documentation for specific orthogonalization managers.
Parameters
X[in/out] On output, the first rank columns of X satisfy

\[ \langle X[i], X[j] \rangle = \delta_{ij} \quad \textrm{and} \quad \langle X, Q[i] \rangle = 0\ . \]

Also,

\[ X_{in}(1:m,1:n) = X_{out}(1:m,1:rank) B(1:rank,1:n) + \sum_i Q[i] C[i] \]

where m is the number of rows in X and n is the number of columns in X.
Q[in] A list of multivector bases specifying the subspaces to be orthogonalized against, satisfying

\[ \langle Q[i], Q[j] \rangle = I \quad\textrm{if}\quad i=j \]

and

\[ \langle Q[i], Q[j] \rangle = 0 \quad\textrm{if}\quad i \neq j\ . \]

C[out] The coefficients of X in the Q[i]. If C[i] is a non-null pointer and C[i] matches the dimensions of X and Q[i], then the coefficients computed during the orthogonalization routine will be stored in the matrix C[i], similar to calling
innerProd( Q[i], X, C[i] );
If C[i] points to a Teuchos::SerialDenseMatrix with size inconsistent with X and Q[i], then a std::invalid_argument exception will be thrown.
Otherwise, if C.size() < i or C[i] is a null pointer, the caller will not have access to the computed coefficients.
B[out] The coefficients of the original X with respect to the computed basis. If B is a non-null pointer and B matches the dimensions of B, then the coefficients computed during the orthogonalization routine will be stored in B, similar to calling
innerProd( Sout, Sin, B );
If B points to a Teuchos::SerialDenseMatrix with size inconsistent with X, then a std::invalid_argument exception will be thrown.
Otherwise, if B is null, the caller will not have access to the computed coefficients.
Note
This matrix is not necessarily triangular (as in a QR factorization); see the documentation of specific orthogonalization managers.
Returns
Rank of the basis computed by this method, less than or equal to the number of columns in X. This specifies how many columns in the returned X and rows in the returned B are valid.

Implements Anasazi::OrthoManager< Scalar, MV >.

Definition at line 240 of file AnasaziTsqrOrthoManager.hpp.

template<class Scalar , class MV >
int Anasazi::TsqrOrthoManager< Scalar, MV >::normalizeOutOfPlace ( MV &  X,
MV &  Q,
mat_ptr  B 
) const
inlinevirtual

Normalize X into Q*B, overwriting X with invalid values.

We expose this interface to applications because TSQR is not able to compute an orthogonal basis in place; it needs scratch space. Applications can exploit this interface to avoid excessive copying of vectors when using TSQR for orthogonalization.

Parameters
X[in/out] Input vector(s) to normalize
Q[out] Normalized output vector(s)
B[out] Normalization coefficients
Returns
Rank of X.
Note
Q must have at least as many columns as X. It may have more columns than X; those columns are ignored.

Implements Anasazi::OutOfPlaceNormalizerMixin< Scalar, MV >.

Definition at line 266 of file AnasaziTsqrOrthoManager.hpp.

template<class Scalar , class MV >
int Anasazi::TsqrOrthoManager< Scalar, MV >::projectAndNormalizeOutOfPlace ( MV &  X_in,
MV &  X_out,
Teuchos::Array< mat_ptr >  C,
mat_ptr  B,
Teuchos::ArrayView< Teuchos::RCP< const MV > >  Q 
) const
inlinevirtual

Project and normalize X_in into X_out; overwrite X_in.

Project X_in against Q, storing projection coefficients in C, and normalize X_in into X_out, storing normalization coefficients in B. On output, X_out has the resulting orthogonal vectors and X_in is overwritten with invalid values.

Parameters
X_in[in/out] On input: The vectors to project against Q and normalize. Overwritten with invalid values on output.
X_out[out] The normalized input vectors after projection against Q.
C[out] Projection coefficients
B[out] Normalization coefficients
Q[in] The orthogonal basis against which to project
Returns
Rank of X_in after projection
Note
We expose this interface to applications for the same reason that we expose normalizeOutOfPlace().

Implements Anasazi::OutOfPlaceNormalizerMixin< Scalar, MV >.

Definition at line 292 of file AnasaziTsqrOrthoManager.hpp.

template<class Scalar , class MV >
magnitude_type Anasazi::TsqrOrthoManager< Scalar, MV >::orthonormError ( const MV &  X) const
inlinevirtual

This method computes the error in orthonormality of a multivector.

This method return some measure of 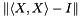$\| \langle X, X \rangle - I \| $.
See the documentation of specific orthogonalization managers.

Implements Anasazi::OrthoManager< Scalar, MV >.

Definition at line 301 of file AnasaziTsqrOrthoManager.hpp.

template<class Scalar , class MV >
magnitude_type Anasazi::TsqrOrthoManager< Scalar, MV >::orthogError ( const MV &  X1,
const MV &  X2 
) const
inlinevirtual

This method computes the error in orthogonality of two multivectors.

This method return some measure of 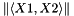$\| \langle X1, X2 \rangle \| $.
See the documentation of specific orthogonalization managers.

Implements Anasazi::OrthoManager< Scalar, MV >.

Definition at line 305 of file AnasaziTsqrOrthoManager.hpp.

The documentation for this class was generated from the following file:
Generated by   doxygen 1.8.5