A read-only, row-oriented interface to a sparse matrix. More...

#include <Tpetra_RowMatrix_decl.hpp>

Inheritance diagram for Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >:

Public Types
Typedefs
typedef Scalar	scalar_type
	The type of the entries in the sparse matrix. More...

typedef LocalOrdinal	local_ordinal_type
	The type of local indices. More...

typedef GlobalOrdinal	global_ordinal_type
	The type of global indices. More...

typedef Node	node_type
	The Kokkos Node type. More...

using	mag_type = typename Kokkos::ArithTraits< Scalar >::mag_type
	Type of a norm result. More...

Public Member Functions
Destructor
virtual	~RowMatrix ()
	Destructor (virtual for memory safety of derived classes). More...

Matrix query methods
virtual Teuchos::RCP< const Teuchos::Comm< int > >	getComm () const =0
	The communicator over which this matrix is distributed. More...

virtual Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > >	getRowMap () const =0
	The Map that describes the distribution of rows over processes. More...

virtual Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > >	getColMap () const =0
	The Map that describes the distribution of columns over processes. More...

virtual Teuchos::RCP< const RowGraph< LocalOrdinal, GlobalOrdinal, Node > >	getGraph () const =0
	The RowGraph associated with this matrix. More...

virtual global_size_t	getGlobalNumRows () const =0
	The global number of rows of this matrix. More...

virtual global_size_t	getGlobalNumCols () const =0
	The global number of columns of this matrix. More...

virtual size_t	getNodeNumRows () const =0
	The number of rows owned by the calling process. More...

virtual size_t	getNodeNumCols () const =0
	The number of columns needed to apply the forward operator on this node. More...

virtual GlobalOrdinal	getIndexBase () const =0
	The index base for global indices in this matrix. More...

virtual global_size_t	getGlobalNumEntries () const =0
	The global number of stored (structurally nonzero) entries. More...

virtual size_t	getNodeNumEntries () const =0
	The local number of stored (structurally nonzero) entries. More...

virtual size_t	getNumEntriesInGlobalRow (GlobalOrdinal globalRow) const =0
	The current number of entries on the calling process in the specified global row. More...

virtual size_t	getNumEntriesInLocalRow (LocalOrdinal localRow) const =0
	The current number of entries on the calling process in the specified local row. More...

virtual size_t	getGlobalMaxNumRowEntries () const =0
	Maximum number of entries in any row of the matrix, over all processes. More...

virtual size_t	getNodeMaxNumRowEntries () const =0
	Maximum number of entries in any row of the matrix, on this process. More...

virtual bool	hasColMap () const =0
	Whether this matrix has a well-defined column Map. More...

virtual bool	isLocallyIndexed () const =0
	Whether matrix indices are locally indexed. More...

virtual bool	isGloballyIndexed () const =0
	Whether matrix indices are globally indexed. More...

virtual bool	isFillComplete () const =0
	Whether fillComplete() has been called. More...

virtual bool	supportsRowViews () const =0
	Whether this object implements getLocalRowView() and getGlobalRowView(). More...

Extraction Methods
virtual void	getGlobalRowCopy (GlobalOrdinal GlobalRow, const Teuchos::ArrayView< GlobalOrdinal > &Indices, const Teuchos::ArrayView< Scalar > &Values, size_t &NumEntries) const =0
	Get a copy of the given global row's entries. More...

virtual void	getLocalRowCopy (LocalOrdinal LocalRow, const Teuchos::ArrayView< LocalOrdinal > &Indices, const Teuchos::ArrayView< Scalar > &Values, size_t &NumEntries) const =0
	Get a copy of the given local row's entries. More...

virtual void	getGlobalRowView (GlobalOrdinal GlobalRow, Teuchos::ArrayView< const GlobalOrdinal > &indices, Teuchos::ArrayView< const Scalar > &values) const =0
	Get a constant, nonpersisting, globally indexed view of the given row of the matrix. More...

virtual void	getLocalRowView (LocalOrdinal LocalRow, Teuchos::ArrayView< const LocalOrdinal > &indices, Teuchos::ArrayView< const Scalar > &values) const =0
	Get a constant, nonpersisting, locally indexed view of the given row of the matrix. More...

virtual LocalOrdinal	getLocalRowViewRaw (const LocalOrdinal lclRow, LocalOrdinal &numEnt, const LocalOrdinal &lclColInds, const Scalar &vals) const
	Get a constant, nonpersisting, locally indexed view of the given row of the matrix, using "raw" pointers instead of Teuchos::ArrayView. More...

virtual void	getLocalDiagCopy (Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &diag) const =0
	Get a copy of the diagonal entries, distributed by the row Map. More...

Mathematical methods
virtual void	leftScale (const Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &x)=0
	Scale the matrix on the left with the given Vector. More...

virtual void	rightScale (const Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &x)=0
	Scale the matrix on the right with the given Vector. More...

virtual mag_type	getFrobeniusNorm () const =0
	The Frobenius norm of the matrix. More...

virtual Teuchos::RCP < RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node > >	add (const Scalar &alpha, const RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node > &A, const Scalar &beta, const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > &domainMap=Teuchos::null, const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > &rangeMap=Teuchos::null, const Teuchos::RCP< Teuchos::ParameterList > &params=Teuchos::null) const
	Return a new RowMatrix which is the result of `betathis + alphaA`. More...

Pure virtual functions to be overridden by subclasses.
virtual Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > >	getDomainMap () const =0
	The Map associated with the domain of this operator, which must be compatible with X.getMap(). More...

virtual Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > >	getRangeMap () const =0
	The Map associated with the range of this operator, which must be compatible with Y.getMap(). More...

virtual void	apply (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &X, MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &Y, Teuchos::ETransp mode=Teuchos::NO_TRANS, Scalar alpha=Teuchos::ScalarTraits< Scalar >::one(), Scalar beta=Teuchos::ScalarTraits< Scalar >::zero()) const =0
	Computes the operator-multivector application. More...

virtual bool	hasTransposeApply () const
	Whether this operator supports applying the transpose or conjugate transpose. More...

Implementation of Packable interface
virtual void	pack (const Teuchos::ArrayView< const LocalOrdinal > &exportLIDs, Teuchos::Array< char > &exports, const Teuchos::ArrayView< size_t > &numPacketsPerLID, size_t &constantNumPackets, Distributor &distor) const
	Pack this object's data for an Import or Export. More...

Detailed Description

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>
class Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >

A read-only, row-oriented interface to a sparse matrix.

Template Parameters

Scalar	The type of the entries in the sparse matrix. Same as the `Scalar` typedef of Operator.
LocalOrdinal	The type of local indices. See the documentation of Map for requirements.
GlobalOrdinal	The type of global indices. See the documentation of Map for requirements.
Node	The Kokkos Node type. See the documentation of Map for requirements.

RowMatrix provides a read-only, row-oriented interface to view the entries of a sparse matrix, which is distributed over one or more (MPI) processes. "Read only" means that you may view the entries, but not modify them. "Row-oriented" means that you may view all the entries owned by the calling process, in any particular row of the matrix that is owned by the calling process.

CrsMatrix implements this interface, but also lets you add or modify entries of the sparse matrix. Ifpack2 provides other implementations of RowMatrix, which do useful things like wrapping an existing matrix to view only certain desired entries.

Definition at line 85 of file Tpetra_RowMatrix_decl.hpp.

Member Typedef Documentation

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

typedef Scalar Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::scalar_type

The type of the entries in the sparse matrix.

Definition at line 94 of file Tpetra_RowMatrix_decl.hpp.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

typedef LocalOrdinal Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::local_ordinal_type

The type of local indices.

Definition at line 96 of file Tpetra_RowMatrix_decl.hpp.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

typedef GlobalOrdinal Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::global_ordinal_type

The type of global indices.

Definition at line 98 of file Tpetra_RowMatrix_decl.hpp.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

typedef Node Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::node_type

The Kokkos Node type.

Definition at line 100 of file Tpetra_RowMatrix_decl.hpp.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

using Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::mag_type = typename Kokkos::ArithTraits<Scalar>::mag_type

Type of a norm result.

This is usually the same as the type of the magnitude (absolute value) of Scalar, but may differ for certain Scalar types.

Definition at line 107 of file Tpetra_RowMatrix_decl.hpp.

Constructor & Destructor Documentation

template<class Scalar , class LocalOrdinal , class GlobalOrdinal , class Node >

Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::~RowMatrix ( )

virtual

Destructor (virtual for memory safety of derived classes).

Definition at line 52 of file Tpetra_RowMatrix_def.hpp.

Member Function Documentation

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual Teuchos::RCP<const Teuchos::Comm<int> > Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getComm ( ) const

pure virtual

The communicator over which this matrix is distributed.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual Teuchos::RCP<const Map<LocalOrdinal,GlobalOrdinal,Node> > Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getRowMap ( ) const

pure virtual

The Map that describes the distribution of rows over processes.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual Teuchos::RCP<const Map<LocalOrdinal,GlobalOrdinal,Node> > Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getColMap ( ) const

pure virtual

The Map that describes the distribution of columns over processes.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual Teuchos::RCP<const RowGraph<LocalOrdinal,GlobalOrdinal,Node> > Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getGraph ( ) const

pure virtual

The RowGraph associated with this matrix.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual global_size_t Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getGlobalNumRows ( ) const

pure virtual

The global number of rows of this matrix.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual global_size_t Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getGlobalNumCols ( ) const

pure virtual

The global number of columns of this matrix.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual size_t Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getNodeNumRows ( ) const

pure virtual

The number of rows owned by the calling process.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual size_t Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getNodeNumCols ( ) const

pure virtual

The number of columns needed to apply the forward operator on this node.

This is the same as the number of elements listed in the column Map. It is not necessarily the same as the number of domain Map elements owned by the calling process.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual GlobalOrdinal Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getIndexBase ( ) const

pure virtual

The index base for global indices in this matrix.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual global_size_t Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getGlobalNumEntries ( ) const

pure virtual

The global number of stored (structurally nonzero) entries.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual size_t Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getNodeNumEntries ( ) const

pure virtual

The local number of stored (structurally nonzero) entries.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual size_t Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getNumEntriesInGlobalRow ( GlobalOrdinal globalRow ) const

pure virtual

The current number of entries on the calling process in the specified global row.

Note that if the row Map is overlapping, then the calling process might not necessarily store all the entries in the row. Some other process might have the rest of the entries.

Returns: Teuchos::OrdinalTraits<size_t>::invalid() if the specified global row does not belong to this graph, else the number of entries.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual size_t Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getNumEntriesInLocalRow ( LocalOrdinal localRow ) const

pure virtual

The current number of entries on the calling process in the specified local row.

Note that if the row Map is overlapping, then the calling process might not necessarily store all the entries in the row. Some other process might have the rest of the entries.

Returns: Teuchos::OrdinalTraits<size_t>::invalid() if the specified local row is not valid for this graph, else the number of entries.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual size_t Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getGlobalMaxNumRowEntries ( ) const

pure virtual

Maximum number of entries in any row of the matrix, over all processes.

Precondition: Subclasses reserve the right to impose preconditions on the matrix's state.

This method only uses the matrix's graph. Explicitly stored zeros count as "entries."

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual size_t Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getNodeMaxNumRowEntries ( ) const

pure virtual

Maximum number of entries in any row of the matrix, on this process.

Precondition: Subclasses reserve the right to impose preconditions on the matrix's state.

This method only uses the matrix's graph. Explicitly stored zeros count as "entries."

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual bool Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::hasColMap ( ) const

pure virtual

Whether this matrix has a well-defined column Map.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual bool Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::isLocallyIndexed ( ) const

pure virtual

Whether matrix indices are locally indexed.

A RowMatrix may store column indices either as global indices (of type GlobalOrdinal), or as local indices (of type LocalOrdinal). In some cases (for example, if the column Map has not been computed), it is not possible to switch from global to local indices without extra work. Furthermore, some operations only work for one or the other case.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual bool Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::isGloballyIndexed ( ) const

pure virtual

Whether matrix indices are globally indexed.

A RowMatrix may store column indices either as global indices (of type GlobalOrdinal), or as local indices (of type LocalOrdinal). In some cases (for example, if the column Map has not been computed), it is not possible to switch from global to local indices without extra work. Furthermore, some operations only work for one or the other case.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual bool Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::isFillComplete ( ) const

pure virtual

Whether fillComplete() has been called.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual bool Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::supportsRowViews ( ) const

pure virtual

Whether this object implements getLocalRowView() and getGlobalRowView().

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual void Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getGlobalRowCopy	(	GlobalOrdinal	GlobalRow,
		const Teuchos::ArrayView< GlobalOrdinal > &	Indices,
		const Teuchos::ArrayView< Scalar > &	Values,
		size_t &	NumEntries
	)		const

pure virtual

Get a copy of the given global row's entries.

This method only gets the entries in the given row that are stored on the calling process. Note that if the matrix has an overlapping row Map, it is possible that the calling process does not store all the entries in that row.

Parameters

GlobalRow	[in] Global index of the row.
Indices	[out] Global indices of the columns corresponding to values.
Values	[out] Matrix values.
NumEntries	[out] Number of stored entries on the calling process; length of Indices and Values.

This method throws std::runtime_error if either Indices or Values is not large enough to hold the data associated with row GlobalRow. If GlobalRow does not belong to the calling process, then the method sets NumIndices to Teuchos::OrdinalTraits<size_t>::invalid(), and does not modify Indices or Values.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual void Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getLocalRowCopy	(	LocalOrdinal	LocalRow,
		const Teuchos::ArrayView< LocalOrdinal > &	Indices,
		const Teuchos::ArrayView< Scalar > &	Values,
		size_t &	NumEntries
	)		const

pure virtual

Get a copy of the given local row's entries.

This method only gets the entries in the given row that are stored on the calling process. Note that if the matrix has an overlapping row Map, it is possible that the calling process does not store all the entries in that row.

Parameters

LocalRow	[in] Local index of the row.
Indices	[out] Local indices of the columns corresponding to values.
Values	[out] Matrix values.
NumEntries	[out] Number of stored entries on the calling process; length of Indices and Values.

This method throws std::runtime_error if either Indices or Values is not large enough to hold the data associated with row LocalRow. If LocalRow does not belong to the calling process, then the method sets NumIndices to Teuchos::OrdinalTraits<size_t>::invalid(), and does not modify Indices or Values.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual void Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getGlobalRowView	(	GlobalOrdinal	GlobalRow,
		Teuchos::ArrayView< const GlobalOrdinal > &	indices,
		Teuchos::ArrayView< const Scalar > &	values
	)		const

pure virtual

Get a constant, nonpersisting, globally indexed view of the given row of the matrix.

The returned views of the column indices and values are not guaranteed to persist beyond the lifetime of this. Furthermore, some RowMatrix implementations allow changing the values, or the indices and values. Any such changes invalidate the returned views.

This method only gets the entries in the given row that are stored on the calling process. Note that if the matrix has an overlapping row Map, it is possible that the calling process does not store all the entries in that row.

Precondition: isGloballyIndexed () && supportsRowViews ()

Postcondition: indices.size () == getNumEntriesInGlobalRow (GlobalRow)

Parameters

GlobalRow	[in] Global index of the row.
Indices	[out] Global indices of the columns corresponding to values.
Values	[out] Matrix values.

If GlobalRow does not belong to this node, then indices is set to null.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual void Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getLocalRowView	(	LocalOrdinal	LocalRow,
		Teuchos::ArrayView< const LocalOrdinal > &	indices,
		Teuchos::ArrayView< const Scalar > &	values
	)		const

pure virtual

Get a constant, nonpersisting, locally indexed view of the given row of the matrix.

The returned views of the column indices and values are not guaranteed to persist beyond the lifetime of this. Furthermore, some RowMatrix implementations allow changing the values, or the indices and values. Any such changes invalidate the returned views.

This method only gets the entries in the given row that are stored on the calling process. Note that if the matrix has an overlapping row Map, it is possible that the calling process does not store all the entries in that row.

Precondition: isLocallyIndexed () && supportsRowViews ()

Postcondition: indices.size () == getNumEntriesInGlobalRow (LocalRow)

Parameters

LocalRow	[in] Local index of the row.
Indices	[out] Local indices of the columns corresponding to values.
Values	[out] Matrix values.

If LocalRow does not belong to this node, then indices is set to null.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal , class Node >

LocalOrdinal Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getLocalRowViewRaw	(	const LocalOrdinal	lclRow,
		LocalOrdinal &	numEnt,
		const LocalOrdinal *&	lclColInds,
		const Scalar *&	vals
	)		const

virtual

Get a constant, nonpersisting, locally indexed view of the given row of the matrix, using "raw" pointers instead of Teuchos::ArrayView.

The returned views of the column indices and values are not guaranteed to persist beyond the lifetime of this. Furthermore, some RowMatrix implementations allow changing the values, or the indices and values. Any such changes invalidate the returned views.

This method only gets the entries in the given row that are stored on the calling process. Note that if the matrix has an overlapping row Map, it is possible that the calling process does not store all the entries in that row.

Precondition: isLocallyIndexed () && supportsRowViews ()

Postcondition: numEnt == getNumEntriesInGlobalRow (LocalRow)

Parameters

lclRow	[in] Local index of the row.
numEnt	[out] Number of entries in the row that are stored on the calling process.
lclColInds	[out] Local indices of the columns corresponding to values.
vals	[out] Matrix values.

Returns: Error code; zero on no error.

Reimplemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >.

Definition at line 596 of file Tpetra_RowMatrix_def.hpp.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual void Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getLocalDiagCopy ( Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & diag ) const

pure virtual

Get a copy of the diagonal entries, distributed by the row Map.

On input, the Vector's Map must be the same as the row Map of the matrix. (That is, this->getRowMap ()->isSameAs (* (diag.getMap ())) == true.)

On return, the entries of diag are filled with the diagonal entries of the matrix stored on this process. Note that if the row Map is overlapping, multiple processes may own the same diagonal element. You may combine these overlapping diagonal elements by doing an Export from the row Map Vector to a range Map Vector.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual void Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::leftScale ( const Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & x )

pure virtual

Scale the matrix on the left with the given Vector.

On return, for all entries i,j in the matrix, 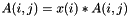$A(i,j) = x(i)*A(i,j)$ .

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual void Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::rightScale ( const Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & x )

pure virtual

Scale the matrix on the right with the given Vector.

On return, for all entries i,j in the matrix, 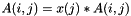$A(i,j) = x(j)*A(i,j)$ .

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual mag_type Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getFrobeniusNorm ( ) const

pure virtual

The Frobenius norm of the matrix.

This method computes and returns the Frobenius norm of the matrix. The Frobenius norm 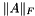$\|A\|_F$ for the matrix 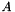$A$ is defined as 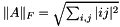$\|A\|_F = \sqrt{ \sum_{i,j} |\a_{ij}|^2 }$ . It has the same value as the Euclidean norm of a vector made by stacking the columns of $A$ .

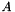Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

Teuchos::RCP< RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node > > Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::add	(	const Scalar &	alpha,
		const RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node > &	A,
		const Scalar &	beta,
		const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > &	domainMap = `Teuchos::null`,
		const Teuchos::RCP< const Map< LocalOrdinal, GlobalOrdinal, Node > > &	rangeMap = `Teuchos::null`,
		const Teuchos::RCP< Teuchos::ParameterList > &	params = `Teuchos::null`
	)		const

virtual

Return a new RowMatrix which is the result of beta*this + alpha*A.

The new RowMatrix is actually a CrsMatrix (which see). Note that RowMatrix is a read-only interface (not counting the left and right scale methods), so it is impossible to implement an in-place add using just that interface.

For brevity, call this matrix B, and the result matrix C. C's row Map will be identical to B's row Map. It is correct, though less efficient, for A and B not to have the same row Maps. We could make C's row Map the union of the two row Maps in that case. However, we don't want row Maps to grow for a repeated sequence of additions with matrices with different row Maps. Furthermore, the fact that the user called this method on B, rather than on A, suggests a preference for using B's distribution. The most reasonable thing to do, then, is to use B's row Map for C.

A and B must have identical or congruent communicators. This method must be called as a collective over B's communicator.

The parameters are optional and may be null. Here are the parameters that this function accepts:

"Call fillComplete" (bool): If true, call fillComplete on the result matrix C. This is true by default.
"Constructor parameters" (sublist): If provided, give these parameters to C's constructor.
"fillComplete parameters" (sublist): If provided, and if "Call fillComplete" is true, then give these parameters to C's fillComplete call.

It is not strictly necessary that a RowMatrix always have a domain and range Map. For example, a CrsMatrix does not have a domain and range Map until after its first fillComplete call. Neither A nor B need to have a domain and range Map in order to call add(). If at least one of them has a domain and range Map, you need not supply a domain and range Map to this method. If you ask this method to call fillComplete on C (it does by default), it will supply the any missing domain or range Maps from either B's or A's (in that order) domain and range Maps. If neither A nor B have a domain and range Map, and if you ask this method to call fillComplete, then you must supply both a domain Map and a range Map to this method.

This method comes with a default implementation, since the RowMatrix interface suffices for implementing it. Subclasses (like CrsMatrix) may override this implementation, for example to improve its performance, given additional knowledge about the subclass. Subclass implementations may need to do a dynamic cast on A in order to know its type.

Reimplemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >.

Definition at line 57 of file Tpetra_RowMatrix_def.hpp.

template<class Scalar , class LocalOrdinal, class GlobalOrdinal , class Node >

void Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >::pack	(	const Teuchos::ArrayView< const LocalOrdinal > &	exportLIDs,
		Teuchos::Array< char > &	exports,
		const Teuchos::ArrayView< size_t > &	numPacketsPerLID,
		size_t &	constantNumPackets,
		Distributor &	distor
	)		const

virtual

Pack this object's data for an Import or Export.

Warning: To be called only by the packAndPrepare method of appropriate classes of DistObject.

Subclasses may override this method to speed up or otherwise improve the implementation by exploiting more specific details of the subclass.

Implements Tpetra::Packable< char, LocalOrdinal >.

Definition at line 296 of file Tpetra_RowMatrix_def.hpp.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual Teuchos::RCP<const Map<LocalOrdinal,GlobalOrdinal,Node> > Tpetra::Operator< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getDomainMap ( ) const

pure virtualinherited

The Map associated with the domain of this operator, which must be compatible with X.getMap().

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Tpetra::CrsMatrixMultiplyOp< Scalar, MatScalar, LocalOrdinal, GlobalOrdinal, Node >, Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >, and Tpetra::details::ApplyOp< Scalar, OperatorType >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual Teuchos::RCP<const Map<LocalOrdinal,GlobalOrdinal,Node> > Tpetra::Operator< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getRangeMap ( ) const

pure virtualinherited

The Map associated with the range of this operator, which must be compatible with Y.getMap().

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Tpetra::CrsMatrixMultiplyOp< Scalar, MatScalar, LocalOrdinal, GlobalOrdinal, Node >, Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >, and Tpetra::details::ApplyOp< Scalar, OperatorType >.

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>

virtual void Tpetra::Operator< Scalar, LocalOrdinal, GlobalOrdinal, Node >::apply	(	const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &	X,
		MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &	Y,
		Teuchos::ETransp	mode = `Teuchos::NO_TRANS`,
		Scalar	alpha = `Teuchos::ScalarTraits< Scalar >::one()`,
		Scalar	beta = `Teuchos::ScalarTraits< Scalar >::zero()`
	)		const

pure virtualinherited

Computes the operator-multivector application.

Loosely, performs 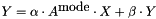$Y = \alpha \cdot A^{\textrm{mode}} \cdot X + \beta \cdot Y$ . However, the details of operation vary according to the values of alpha and beta. Specifically

if beta == 0, apply() must overwrite Y, so that any values in Y (including NaNs) are ignored.
if alpha == 0, apply() may short-circuit the operator, so that any values in X (including NaNs) are ignored.

Implemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Tpetra::CrsMatrixMultiplyOp< Scalar, MatScalar, LocalOrdinal, GlobalOrdinal, Node >, and Tpetra::details::ApplyOp< Scalar, OperatorType >.

template<class Scalar , class LocalOrdinal , class GlobalOrdinal , class Node >

bool Tpetra::Operator< Scalar, LocalOrdinal, GlobalOrdinal, Node >::hasTransposeApply ( ) const

virtualinherited

Whether this operator supports applying the transpose or conjugate transpose.

By default, this returns false. Subclasses must override this method if they can support apply() with mode=Teuchos::TRANS or mode=Teuchos::CONJ_TRANS.

Reimplemented in Tpetra::CrsMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >, Tpetra::CrsMatrixMultiplyOp< Scalar, MatScalar, LocalOrdinal, GlobalOrdinal, Node >, Tpetra::BlockCrsMatrix< Scalar, LO, GO, Node >, and Tpetra::details::ApplyOp< Scalar, OperatorType >.

Definition at line 138 of file Tpetra_Operator.hpp.

The documentation for this class was generated from the following files:

Public Types

Public Member Functions

Implementation of Packable interface

Detailed Description

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node> class Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

template<class Scalar, class LocalOrdinal, class GlobalOrdinal, class Node>
class Tpetra::RowMatrix< Scalar, LocalOrdinal, GlobalOrdinal, Node >