|
Tpetra parallel linear algebra
Version of the Day
|
|
Tpetra parallel linear algebra
Version of the Day
|
One or more distributed dense vectors. More...
#include <Tpetra_MultiVector_decl.hpp>

Public Types | |
Typedefs to facilitate template metaprogramming. | |
| using | scalar_type = Scalar |
| The type of each entry in the MultiVector. More... | |
| using | impl_scalar_type = typename Kokkos::Details::ArithTraits< Scalar >::val_type |
The type used internally in place of Scalar. More... | |
| using | map_type = Map< LocalOrdinal, GlobalOrdinal, Node > |
| The type of the Map specialization used by this class. More... | |
| using | local_ordinal_type = typename map_type::local_ordinal_type |
| The type of local indices that this class uses. More... | |
| using | global_ordinal_type = typename map_type::global_ordinal_type |
| The type of global indices that this class uses. More... | |
| using | device_type = typename map_type::device_type |
| This class' preferred Kokkos device type. More... | |
| using | node_type = typename map_type::node_type |
| Legacy thing that you should not use any more. More... | |
| using | dot_type = typename Kokkos::Details::InnerProductSpaceTraits< impl_scalar_type >::dot_type |
| Type of an inner ("dot") product result. More... | |
| using | mag_type = typename Kokkos::ArithTraits< impl_scalar_type >::mag_type |
| Type of a norm result. More... | |
| using | execution_space = typename device_type::execution_space |
| Type of the (new) Kokkos execution space. More... | |
| using | dual_view_type = Kokkos::DualView< impl_scalar_type **, Kokkos::LayoutLeft, execution_space > |
| Kokkos::DualView specialization used by this class. More... | |
Typedefs | |
| using | packet_type = typename::Kokkos::Details::ArithTraits< Scalar >::val_type |
| The type of each datum being sent or received in an Import or Export. More... | |
Public Member Functions | |
| virtual void | removeEmptyProcessesInPlace (const Teuchos::RCP< const map_type > &newMap) |
| Remove processes owning zero rows from the Map and their communicator. More... | |
| void | setCopyOrView (const Teuchos::DataAccess copyOrView) |
| Set whether this has copy (copyOrView = Teuchos::Copy) or view (copyOrView = Teuchos::View) semantics. More... | |
| Teuchos::DataAccess | getCopyOrView () const |
| Get whether this has copy (copyOrView = Teuchos::Copy) or view (copyOrView = Teuchos::View) semantics. More... | |
| void | assign (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &src) |
Copy the contents of src into *this (deep copy). More... | |
| bool | isSameSize (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &vec) const |
Get a copy or view of a subset of rows and/or columns | |
The following methods get either a (deep) copy or a view (shallow copy) of a subset of rows and/or columns of the MultiVector. They return one of the following:
We prefer use of Kokkos classes to Teuchos Memory Management Classes. In particular, Teuchos::ArrayRCP reference counts are not thread safe, while Kokkos::View (and Kokkos::DualView) reference counts are thread safe. Not all of these methods are valid for a particular MultiVector. For instance, calling a method that accesses a view of the data in a 1-D format (i.e., get1dView) requires that the target MultiVector have constant stride. This category of methods also includes sync(), modify(), and getLocalView(), which help MultiVector implement DualView semantics. | |
| Teuchos::RCP< MultiVector < Scalar, LocalOrdinal, GlobalOrdinal, Node > > | subCopy (const Teuchos::Range1D &colRng) const |
| Return a MultiVector with copies of selected columns. More... | |
| Teuchos::RCP< MultiVector < Scalar, LocalOrdinal, GlobalOrdinal, Node > > | subCopy (const Teuchos::ArrayView< const size_t > &cols) const |
| Return a MultiVector with copies of selected columns. More... | |
| Teuchos::RCP< const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > | subView (const Teuchos::Range1D &colRng) const |
| Return a const MultiVector with const views of selected columns. More... | |
| Teuchos::RCP< const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > | subView (const Teuchos::ArrayView< const size_t > &cols) const |
| Return a const MultiVector with const views of selected columns. More... | |
| Teuchos::RCP< MultiVector < Scalar, LocalOrdinal, GlobalOrdinal, Node > > | subViewNonConst (const Teuchos::Range1D &colRng) |
| Return a MultiVector with views of selected columns. More... | |
| Teuchos::RCP< MultiVector < Scalar, LocalOrdinal, GlobalOrdinal, Node > > | subViewNonConst (const Teuchos::ArrayView< const size_t > &cols) |
| Return a MultiVector with views of selected columns. More... | |
| Teuchos::RCP< const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > | offsetView (const Teuchos::RCP< const map_type > &subMap, const size_t offset) const |
| Return a const view of a subset of rows. More... | |
| Teuchos::RCP< MultiVector < Scalar, LocalOrdinal, GlobalOrdinal, Node > > | offsetViewNonConst (const Teuchos::RCP< const map_type > &subMap, const size_t offset) |
| Return a nonconst view of a subset of rows. More... | |
| Teuchos::RCP< const Vector < Scalar, LocalOrdinal, GlobalOrdinal, Node > > | getVector (const size_t j) const |
| Return a Vector which is a const view of column j. More... | |
| Teuchos::RCP< Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > | getVectorNonConst (const size_t j) |
| Return a Vector which is a nonconst view of column j. More... | |
| Teuchos::ArrayRCP< const Scalar > | getData (size_t j) const |
| Const view of the local values in a particular vector of this multivector. More... | |
| Teuchos::ArrayRCP< Scalar > | getDataNonConst (size_t j) |
| View of the local values in a particular vector of this multivector. More... | |
| void | get1dCopy (const Teuchos::ArrayView< Scalar > &A, const size_t LDA) const |
| Fill the given array with a copy of this multivector's local values. More... | |
| void | get2dCopy (const Teuchos::ArrayView< const Teuchos::ArrayView< Scalar > > &ArrayOfPtrs) const |
| Fill the given array with a copy of this multivector's local values. More... | |
| Teuchos::ArrayRCP< const Scalar > | get1dView () const |
| Const persisting (1-D) view of this multivector's local values. More... | |
| Teuchos::ArrayRCP < Teuchos::ArrayRCP< const Scalar > > | get2dView () const |
| Return const persisting pointers to values. More... | |
| Teuchos::ArrayRCP< Scalar > | get1dViewNonConst () |
| Nonconst persisting (1-D) view of this multivector's local values. More... | |
| Teuchos::ArrayRCP < Teuchos::ArrayRCP< Scalar > > | get2dViewNonConst () |
| Return non-const persisting pointers to values. More... | |
| void | clear_sync_state () |
| Clear "modified" flags on both host and device sides. More... | |
| template<class TargetDeviceType > | |
| void | sync () |
| Update data on device or host only if data in the other space has been marked as modified. More... | |
| void | sync_host () |
| Synchronize to Host. More... | |
| void | sync_device () |
| Synchronize to Device. More... | |
| template<class TargetDeviceType > | |
| bool | need_sync () const |
| Whether this MultiVector needs synchronization to the given space. More... | |
| bool | need_sync_host () const |
| Whether this MultiVector needs synchronization to the host. More... | |
| bool | need_sync_device () const |
| Whether this MultiVector needs synchronization to the device. More... | |
| template<class TargetDeviceType > | |
| void | modify () |
Mark data as modified on the given device TargetDeviceType. More... | |
| void | modify_device () |
| Mark data as modified on the device side. More... | |
| void | modify_host () |
| Mark data as modified on the host side. More... | |
| template<class TargetDeviceType > | |
| Kokkos::Impl::if_c < std::is_same< typename device_type::memory_space, typename TargetDeviceType::memory_space > ::value, typename dual_view_type::t_dev, typename dual_view_type::t_host >::type | getLocalView () const |
| Return a view of the local data on a specific device. More... | |
| dual_view_type::t_host | getLocalViewHost () const |
| A local Kokkos::View of host memory. More... | |
| dual_view_type::t_dev | getLocalViewDevice () const |
| A local Kokkos::View of device memory. More... | |
Mathematical methods | |
| void | dot (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &A, const Teuchos::ArrayView< dot_type > &dots) const |
| Compute the dot product of each corresponding pair of vectors (columns) in A and B. More... | |
| template<typename T > | |
| std::enable_if< !(std::is_same < dot_type, T >::value), void > ::type | dot (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &A, const Teuchos::ArrayView< T > &dots) const |
| Compute the dot product of each corresponding pair of vectors (columns) in A and B. More... | |
| template<typename T > | |
| std::enable_if< !(std::is_same < dot_type, T >::value), void > ::type | dot (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &A, std::vector< T > &dots) const |
| Like the above dot() overload, but for std::vector output. More... | |
| void | dot (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &A, const Kokkos::View< dot_type *, Kokkos::HostSpace > &norms) const |
| Compute the dot product of each corresponding pair of vectors (columns) in A and B, storing the result in a device View. More... | |
| template<class ViewType > | |
| void | dot (typename std::enable_if< std::is_same< typename ViewType::value_type, dot_type >::value &&std::is_same< typename ViewType::memory_space, typename device_type::memory_space >::value, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >>::type &A, const ViewType &dots) const |
| template<typename T > | |
| std::enable_if< !(std::is_same < dot_type, T >::value), void > ::type | dot (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &A, const Kokkos::View< T *, device_type > &dots) const |
| Compute the dot product of each corresponding pair of vectors (columns) in A and B, storing the result in a device view. More... | |
| void | abs (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &A) |
| Put element-wise absolute values of input Multi-vector in target: A = abs(this) More... | |
| void | reciprocal (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &A) |
| Put element-wise reciprocal values of input Multi-vector in target, this(i,j) = 1/A(i,j). More... | |
| void | scale (const Scalar &alpha) |
Scale in place: this = alpha*this. More... | |
| void | scale (const Teuchos::ArrayView< const Scalar > &alpha) |
Scale each column in place: this[j] = alpha[j]*this[j]. More... | |
| void | scale (const Kokkos::View< const impl_scalar_type *, device_type > &alpha) |
Scale each column in place: this[j] = alpha[j]*this[j]. More... | |
| void | scale (const Scalar &alpha, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &A) |
Scale in place: this = alpha * A. More... | |
| void | update (const Scalar &alpha, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &A, const Scalar &beta) |
Update: this = beta*this + alpha*A. More... | |
| void | update (const Scalar &alpha, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &A, const Scalar &beta, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &B, const Scalar &gamma) |
Update: this = gamma*this + alpha*A + beta*B. More... | |
| void | norm1 (const Kokkos::View< mag_type *, Kokkos::HostSpace > &norms) const |
| Compute the one-norm of each vector (column), storing the result in a host view. More... | |
| template<class ViewType > | |
| std::enable_if< std::is_same < typename ViewType::value_type, mag_type > ::value &&std::is_same < typename ViewType::memory_space, typename device_type::memory_space > ::value >::type | norm1 (const ViewType &norms) const |
| template<typename T > | |
| std::enable_if< !(std::is_same < mag_type, T >::value), void > ::type | norm1 (const Kokkos::View< T *, device_type > &norms) const |
| Compute the one-norm of each vector (column), storing the result in a device view. More... | |
| void | norm1 (const Teuchos::ArrayView< mag_type > &norms) const |
| Compute the one-norm of each vector (column). More... | |
| template<typename T > | |
| std::enable_if< !(std::is_same < mag_type, T >::value), void > ::type | norm1 (const Teuchos::ArrayView< T > &norms) const |
| Compute the one-norm of each vector (column). More... | |
| void | norm2 (const Kokkos::View< mag_type *, Kokkos::HostSpace > &norms) const |
| Compute the two-norm of each vector (column), storing the result in a host View. More... | |
| template<class ViewType > | |
| std::enable_if< std::is_same < typename ViewType::value_type, mag_type > ::value &&std::is_same < typename ViewType::memory_space, typename device_type::memory_space > ::value >::type | norm2 (const ViewType &norms) const |
| template<typename T > | |
| std::enable_if< !(std::is_same < mag_type, T >::value), void > ::type | norm2 (const Kokkos::View< T *, device_type > &norms) const |
| Compute the two-norm of each vector (column), storing the result in a device view. More... | |
| void | norm2 (const Teuchos::ArrayView< mag_type > &norms) const |
| Compute the two-norm of each vector (column). More... | |
| template<typename T > | |
| std::enable_if< !(std::is_same < mag_type, T >::value), void > ::type | norm2 (const Teuchos::ArrayView< T > &norms) const |
| Compute the two-norm of each vector (column). More... | |
| void | normInf (const Kokkos::View< mag_type *, Kokkos::HostSpace > &norms) const |
| Compute the infinity-norm of each vector (column), storing the result in a host View. More... | |
| template<class ViewType > | |
| std::enable_if< std::is_same < typename ViewType::value_type, mag_type > ::value &&std::is_same < typename ViewType::memory_space, typename device_type::memory_space > ::value >::type | normInf (const ViewType &norms) const |
| template<typename T > | |
| std::enable_if< !(std::is_same < mag_type, T >::value), void > ::type | normInf (const Kokkos::View< T *, device_type > &norms) const |
| Compute the infinity-norm of each vector (column), storing the result in a device view. More... | |
| void | normInf (const Teuchos::ArrayView< mag_type > &norms) const |
| Compute the infinity-norm of each vector (column), storing the result in a Teuchos::ArrayView. More... | |
| template<typename T > | |
| std::enable_if< !(std::is_same < mag_type, T >::value), void > ::type | normInf (const Teuchos::ArrayView< T > &norms) const |
| Compute the infinity-norm of each vector (column), storing the result in a Teuchos::ArrayView. More... | |
| void | meanValue (const Teuchos::ArrayView< impl_scalar_type > &means) const |
| Compute mean (average) value of each column. More... | |
| template<typename T > | |
| std::enable_if<!std::is_same < impl_scalar_type, T >::value, void >::type | meanValue (const Teuchos::ArrayView< T > &means) const |
| void | multiply (Teuchos::ETransp transA, Teuchos::ETransp transB, const Scalar &alpha, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &A, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &B, const Scalar &beta) |
Matrix-matrix multiplication: this = beta*this + alpha*op(A)*op(B). More... | |
| void | elementWiseMultiply (Scalar scalarAB, const Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &A, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &B, Scalar scalarThis) |
| Multiply a Vector A elementwise by a MultiVector B. More... | |
Attribute access functions | |
| size_t | getNumVectors () const |
| Number of columns in the multivector. More... | |
| size_t | getLocalLength () const |
| Local number of rows on the calling process. More... | |
| global_size_t | getGlobalLength () const |
| Global number of rows in the multivector. More... | |
| size_t | getStride () const |
| Stride between columns in the multivector. More... | |
| bool | isConstantStride () const |
| Whether this multivector has constant stride between columns. More... | |
Overridden from Teuchos::Describable | |
| virtual std::string | description () const |
| A simple one-line description of this object. More... | |
| virtual void | describe (Teuchos::FancyOStream &out, const Teuchos::EVerbosityLevel verbLevel=Teuchos::Describable::verbLevel_default) const |
| Print the object with the given verbosity level to a FancyOStream. More... | |
Public methods for redistributing data | |
| void | doImport (const SrcDistObject &source, const Import< LocalOrdinal, GlobalOrdinal, Node > &importer, const CombineMode CM, const bool restrictedMode=false) |
| Import data into this object using an Import object ("forward mode"). More... | |
| void | doImport (const SrcDistObject &source, const Export< LocalOrdinal, GlobalOrdinal, Node > &exporter, const CombineMode CM, const bool restrictedMode=false) |
| Import data into this object using an Export object ("reverse mode"). More... | |
| void | doExport (const SrcDistObject &source, const Export< LocalOrdinal, GlobalOrdinal, Node > &exporter, const CombineMode CM, const bool restrictedMode=false) |
| Export data into this object using an Export object ("forward mode"). More... | |
| void | doExport (const SrcDistObject &source, const Import< LocalOrdinal, GlobalOrdinal, Node > &importer, const CombineMode CM, const bool restrictedMode=false) |
| Export data into this object using an Import object ("reverse mode"). More... | |
Attribute accessor methods | |
| bool | isDistributed () const |
| Whether this is a globally distributed object. More... | |
| virtual Teuchos::RCP< const map_type > | getMap () const |
| The Map describing the parallel distribution of this object. More... | |
I/O methods | |
| void | print (std::ostream &os) const |
| Print this object to the given output stream. More... | |
Methods for use only by experts | |
| virtual void | removeEmptyProcessesInPlace (const Teuchos::RCP< const map_type > &newMap) |
| Remove processes which contain no entries in this object's Map. More... | |
Protected Member Functions | |
| virtual void | doTransfer (const SrcDistObject &src, const ::Tpetra::Details::Transfer< local_ordinal_type, global_ordinal_type, node_type > &transfer, const char modeString[], const ReverseOption revOp, const CombineMode CM, const bool restrictedMode) |
| Redistribute data across (MPI) processes. More... | |
| virtual bool | reallocArraysForNumPacketsPerLid (const size_t numExportLIDs, const size_t numImportLIDs) |
| Reallocate numExportPacketsPerLID_ and/or numImportPacketsPerLID_, if necessary. More... | |
| virtual void | doTransferNew (const SrcDistObject &src, const CombineMode CM, const size_t numSameIDs, const Kokkos::DualView< const local_ordinal_type *, buffer_device_type > &permuteToLIDs, const Kokkos::DualView< const local_ordinal_type *, buffer_device_type > &permuteFromLIDs, const Kokkos::DualView< const local_ordinal_type *, buffer_device_type > &remoteLIDs, const Kokkos::DualView< const local_ordinal_type *, buffer_device_type > &exportLIDs, Distributor &distor, const ReverseOption revOp, const bool commOnHost, const bool restrictedMode) |
| Implementation detail of doTransfer. More... | |
Misc. implementation details | |
| std::string | descriptionImpl (const std::string &className) const |
| Implementation of description() for this class, and its subclass Vector. More... | |
| std::string | localDescribeToString (const Teuchos::EVerbosityLevel vl) const |
| Print the calling process' verbose describe() information to the returned string. More... | |
| void | describeImpl (Teuchos::FancyOStream &out, const std::string &className, const Teuchos::EVerbosityLevel verbLevel=Teuchos::Describable::verbLevel_default) const |
| Implementation of describe() for this class, and its subclass Vector. More... | |
| bool | vectorIndexOutOfRange (const size_t VectorIndex) const |
| template<class T > | |
| Teuchos::ArrayRCP< T > | getSubArrayRCP (Teuchos::ArrayRCP< T > arr, size_t j) const |
| Persisting view of j-th column in the given ArrayRCP. More... | |
| size_t | getOrigNumLocalRows () const |
| "Original" number of rows in the (local) data. More... | |
| size_t | getOrigNumLocalCols () const |
| "Original" number of columns in the (local) data. More... | |
Protected Attributes | |
| dual_view_type | view_ |
| The Kokkos::DualView containing the MultiVector's data. More... | |
| dual_view_type | origView_ |
| The "original view" of the MultiVector's data. More... | |
| Teuchos::Array< size_t > | whichVectors_ |
| Indices of columns this multivector is viewing. More... | |
Related Functions | |
(Note that these are not member functions.) | |
| template<class DS , class DL , class DG , class DN , class SS , class SL , class SG , class SN > | |
| void | deep_copy (MultiVector< DS, DL, DG, DN > &dst, const MultiVector< SS, SL, SG, SN > &src) |
Copy the contents of the MultiVector src into dst. More... | |
| template<class ST , class LO , class GO , class NT > | |
| MultiVector< ST, LO, GO, NT > | createCopy (const MultiVector< ST, LO, GO, NT > &src) |
| Return a deep copy of the given MultiVector. More... | |
Methods implemented by subclasses and used by doTransfer(). | |
The doTransfer() method uses the subclass' implementations of these methods to implement data transfer. Subclasses of DistObject must implement these methods. This is an instance of the Template Method Pattern. ("Template" here doesn't mean "C++ template"; it means "pattern with holes that are filled in by the subclass' method implementations.") | |
| Teuchos::RCP< const map_type > | map_ |
| The Map over which this object is distributed. More... | |
| Kokkos::DualView< packet_type *, buffer_device_type > | imports_ |
| Buffer into which packed data are imported (received from other processes). More... | |
| Kokkos::DualView< size_t *, buffer_device_type > | numImportPacketsPerLID_ |
| Number of packets to receive for each receive operation. More... | |
| Kokkos::DualView< packet_type *, buffer_device_type > | exports_ |
| Buffer from which packed data are exported (sent to other processes). More... | |
| Kokkos::DualView< size_t *, buffer_device_type > | numExportPacketsPerLID_ |
| Number of packets to send for each send operation. More... | |
| virtual void | copyAndPermute (const SrcDistObject &source, const size_t numSameIDs, const Kokkos::DualView< const local_ordinal_type *, buffer_device_type > &permuteToLIDs, const Kokkos::DualView< const local_ordinal_type *, buffer_device_type > &permuteFromLIDs) |
| Perform copies and permutations that are local to the calling (MPI) process. More... | |
| virtual void | packAndPrepare (const SrcDistObject &source, const Kokkos::DualView< const local_ordinal_type *, buffer_device_type > &exportLIDs, Kokkos::DualView< packet_type *, buffer_device_type > &exports, Kokkos::DualView< size_t *, buffer_device_type > numPacketsPerLID, size_t &constantNumPackets, Distributor &distor) |
| Pack data and metadata for communication (sends). More... | |
| virtual void | unpackAndCombine (const Kokkos::DualView< const local_ordinal_type *, buffer_device_type > &importLIDs, Kokkos::DualView< packet_type *, buffer_device_type > imports, Kokkos::DualView< size_t *, buffer_device_type > numPacketsPerLID, const size_t constantNumPackets, Distributor &distor, const CombineMode combineMode) |
| Perform any unpacking and combining after communication. More... | |
| std::unique_ptr< std::string > | createPrefix (const char className[], const char methodName[]) const |
| bool | reallocImportsIfNeeded (const size_t newSize, const bool verbose, const std::string *prefix) |
| Reallocate imports_ if needed. More... | |
Constructors and destructor | |
| MultiVector () | |
| Default constructor: makes a MultiVector with no rows or columns. More... | |
| MultiVector (const Teuchos::RCP< const map_type > &map, const size_t numVecs, const bool zeroOut=true) | |
| Basic constuctor. More... | |
| MultiVector (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &source, const Teuchos::DataAccess copyOrView) | |
| Copy constructor, with option to do deep or shallow copy. More... | |
| MultiVector (const Teuchos::RCP< const map_type > &map, const Teuchos::ArrayView< const Scalar > &A, const size_t LDA, const size_t NumVectors) | |
| Create multivector by copying two-dimensional array of local data. More... | |
| MultiVector (const Teuchos::RCP< const map_type > &map, const Teuchos::ArrayView< const Teuchos::ArrayView< const Scalar > > &ArrayOfPtrs, const size_t NumVectors) | |
| Create multivector by copying array of views of local data. More... | |
| MultiVector (const Teuchos::RCP< const map_type > &map, const dual_view_type &view) | |
| Constructor, that takes a Kokkos::DualView of the MultiVector's data, and returns a MultiVector that views those data. More... | |
| MultiVector (const Teuchos::RCP< const map_type > &map, const typename dual_view_type::t_dev &d_view) | |
| Constructor, that takes a Kokkos::View of the MultiVector's data (living in the Device's memory space), and returns a MultiVector that views those data. More... | |
| MultiVector (const Teuchos::RCP< const map_type > &map, const dual_view_type &view, const dual_view_type &origView) | |
| Expert mode constructor, that takes a Kokkos::DualView of the MultiVector's data and the "original" Kokkos::DualView of the data, and returns a MultiVector that views those data. More... | |
| MultiVector (const Teuchos::RCP< const map_type > &map, const dual_view_type &view, const Teuchos::ArrayView< const size_t > &whichVectors) | |
| Expert mode constructor for noncontiguous views. More... | |
| MultiVector (const Teuchos::RCP< const map_type > &map, const dual_view_type &view, const dual_view_type &origView, const Teuchos::ArrayView< const size_t > &whichVectors) | |
| Expert mode constructor for noncontiguous views, with original view. More... | |
| MultiVector (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &X, const Teuchos::RCP< const map_type > &subMap, const local_ordinal_type rowOffset=0) | |
| "Offset view" constructor; make a view of a contiguous subset of rows on each process. More... | |
| MultiVector (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &X, const map_type &subMap, const size_t offset=0) | |
"Offset view" constructor, that takes the new Map as a const Map& rather than by RCP. More... | |
| MultiVector (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &)=default | |
| Copy constructor (shallow copy). More... | |
| MultiVector (MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &&)=default | |
| Move constructor (shallow move). More... | |
| MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | operator= (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &)=default |
| Copy assigment (shallow copy). More... | |
| MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | operator= (MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &&)=default |
| Move assigment (shallow move). More... | |
| virtual | ~MultiVector ()=default |
| Destructor (virtual for memory safety of derived classes). More... | |
| void | swap (MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &mv) |
Swap contents of mv with contents of *this. More... | |
| MultiVector (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &X, const size_t j) | |
| Single-column subview constructor, for derived classes ONLY. More... | |
Post-construction modification routines | |
| static const bool | useAtomicUpdatesByDefault |
| Whether sumIntoLocalValue and sumIntoGlobalValue should use atomic updates by default. More... | |
| void | replaceGlobalValue (const GlobalOrdinal gblRow, const size_t col, const impl_scalar_type &value) const |
| Replace value in host memory, using global row index. More... | |
| template<typename T > | |
| std::enable_if<!std::is_same < T, impl_scalar_type >::value &&std::is_convertible< T, impl_scalar_type >::value, void >::type | replaceGlobalValue (GlobalOrdinal globalRow, size_t col, const T &value) const |
| Like the above replaceGlobalValue, but only enabled if T differs from impl_scalar_type. More... | |
| void | sumIntoGlobalValue (const GlobalOrdinal gblRow, const size_t col, const impl_scalar_type &value, const bool atomic=useAtomicUpdatesByDefault) const |
| Update (+=) a value in host memory, using global row index. More... | |
| template<typename T > | |
| std::enable_if<!std::is_same < T, impl_scalar_type >::value &&std::is_convertible< T, impl_scalar_type >::value, void >::type | sumIntoGlobalValue (const GlobalOrdinal gblRow, const size_t col, const T &val, const bool atomic=useAtomicUpdatesByDefault) const |
| Like the above sumIntoGlobalValue, but only enabled if T differs from impl_scalar_type. More... | |
| void | replaceLocalValue (const LocalOrdinal lclRow, const size_t col, const impl_scalar_type &value) const |
| Replace value in host memory, using local (row) index. More... | |
| template<typename T > | |
| std::enable_if<!std::is_same < T, impl_scalar_type >::value &&std::is_convertible< T, impl_scalar_type >::value, void >::type | replaceLocalValue (const LocalOrdinal lclRow, const size_t col, const T &val) const |
| Like the above replaceLocalValue, but only enabled if T differs from impl_scalar_type. More... | |
| void | sumIntoLocalValue (const LocalOrdinal lclRow, const size_t col, const impl_scalar_type &val, const bool atomic=useAtomicUpdatesByDefault) const |
| Update (+=) a value in host memory, using local row index. More... | |
| template<typename T > | |
| std::enable_if<!std::is_same < T, impl_scalar_type >::value &&std::is_convertible< T, impl_scalar_type >::value, void >::type | sumIntoLocalValue (const LocalOrdinal lclRow, const size_t col, const T &val, const bool atomic=useAtomicUpdatesByDefault) const |
| Like the above sumIntoLocalValue, but only enabled if T differs from impl_scalar_type. More... | |
| void | putScalar (const Scalar &value) |
| Set all values in the multivector with the given value. More... | |
| template<typename T > | |
| std::enable_if<!std::is_same < T, impl_scalar_type >::value &&std::is_convertible< T, impl_scalar_type >::value, void >::type | putScalar (const T &value) |
| Set all values in the multivector with the given value. More... | |
| void | randomize () |
| Set all values in the multivector to pseudorandom numbers. More... | |
| void | randomize (const Scalar &minVal, const Scalar &maxVal) |
| Set all values in the multivector to pseudorandom numbers in the given range. More... | |
| void | replaceMap (const Teuchos::RCP< const map_type > &map) |
| Replace the underlying Map in place. More... | |
| void | reduce () |
| Sum values of a locally replicated multivector across all processes. More... | |
Implementation of Tpetra::DistObject | |
| using | buffer_device_type = typename DistObject< scalar_type, local_ordinal_type, global_ordinal_type, node_type >::buffer_device_type |
| Kokkos::Device specialization for communication buffers. More... | |
| virtual bool | checkSizes (const SrcDistObject &sourceObj) |
Whether data redistribution between sourceObj and this object is legal. More... | |
| virtual size_t | constantNumberOfPackets () const |
| Number of packets to send per LID. More... | |
| virtual void | copyAndPermute (const SrcDistObject &sourceObj, const size_t numSameIDs, const Kokkos::DualView< const local_ordinal_type *, buffer_device_type > &permuteToLIDs, const Kokkos::DualView< const local_ordinal_type *, buffer_device_type > &permuteFromLIDs) |
| virtual void | packAndPrepare (const SrcDistObject &sourceObj, const Kokkos::DualView< const local_ordinal_type *, buffer_device_type > &exportLIDs, Kokkos::DualView< impl_scalar_type *, buffer_device_type > &exports, Kokkos::DualView< size_t *, buffer_device_type >, size_t &constantNumPackets, Distributor &) |
| virtual void | unpackAndCombine (const Kokkos::DualView< const local_ordinal_type *, buffer_device_type > &importLIDs, Kokkos::DualView< impl_scalar_type *, buffer_device_type > imports, Kokkos::DualView< size_t *, buffer_device_type >, const size_t constantNumPackets, Distributor &, const CombineMode CM) |
One or more distributed dense vectors.
A "multivector" contains one or more dense vectors. All the vectors in a multivector have the same distribution of rows in parallel over the communicator used to create the multivector. Multivectors containing more than one vector are useful for algorithms that solve multiple linear systems at once, or that solve for a cluster of eigenvalues and their corresponding eigenvectors at once. These "block" algorithms often have accuracy or performance advantages over corresponding algorithms that solve for only one vector at a time. For example, working with multiple vectors at a time allows Tpetra to use faster BLAS 3 routines for local computations. It may also reduce the number of parallel reductions.
The Vector class implements the MultiVector interface, so if you only wish to work with a single vector at a time, you may simply use Vector instead of MultiVector. However, if you are writing solvers or preconditioners, you would do better to write to the MultiVector interface and always assume that each MultiVector contains more than one vector. This will make your solver or preconditioner more compatible with other Trilinos packages, and it will also let you exploit the performance optimizations mentioned above.
| Scalar | The type of each entry of the multivector. (You can use real-valued or complex-valued types here, unlike in Epetra, where the scalar type is always double.) |
| LocalOrdinal | The type of local indices. See the documentation of Map for requirements. |
| GlobalOrdinal | The type of global indices. See the documentation of Map for requirements. |
| Node | The Kokkos Node type. |
Before reading the rest of this documentation, it helps to know a little bit about Kokkos. In particular, you should know about execution spaces, memory spaces, and shallow copy semantics. You should also know something about the Teuchos memory management classes, in particular Teuchos::RCP, though it helps to know a bit about Teuchos::ArrayRCP and Teuchos::ArrayView as well. You may also want to know about the differences between BLAS 1, 2, and 3 operations, and learn a little bit about MPI (the Message Passing Interface for distributed-memory programming). You won't have to use MPI directly to use MultiVector, but it helps to be familiar with the general idea of distributed storage of data over a communicator.
A MultiVector is a view of data. A view behaves like a pointer; it provides access to the original multivector's data without copying the data. This means that the copy constructor and assignment operator (operator=) do shallow copies. They do not copy the data; they just copy pointers and other "metadata." If you would like to copy a MultiVector into an existing MultiVector, call the nonmember function deep_copy(). If you would like to create a new MultiVector which is a deep copy of an existing MultiVector, call the nonmember function createCopy(), or use the two-argument copy constructor with Teuchos::Copy as the second argument.
Views have the additional property that they automatically handle deallocation. They use reference counting for this, much like how std::shared_ptr works. That means you do not have to worry about "freeing" a MultiVector after it has been created. Furthermore, you may pass shallow copies around without needing to worry about which is the "master" view of the data. There is no "master" view of the data; when the last view falls out of scope, the data will be deallocated.
This is what the documentation means when it speaks of view semantics. The opposite of that is copy or container semantics, where the copy constructor and operator= do deep copies (of the data). We say that "std::vector has container semantics," and "MultiVector has view
semantics."
MultiVector also has "subview" methods that give results analogous to the Kokkos::subview() function. That is, they return a MultiVector which views some subset of another MultiVector's rows and columns. The subset of columns in a view need not be contiguous. For example, given a multivector X with 43 columns, it is possible to have a multivector Y which is a view of columns 1, 3, and 42 (zero-based indices) of X. We call such multivectors noncontiguous. They have the the property that isConstantStride() returns false.
Noncontiguous multivectors lose some performance advantages. For example, local computations may be slower, since Tpetra cannot use BLAS 3 routines (e.g., matrix-matrix multiply) on a noncontiguous multivectors without copying into temporary contiguous storage. For performance reasons, if you get a Kokkos::View of a noncontiguous MultiVector's local data, it does not correspond to the columns that the MultiVector views.
Tpetra was designed to perform well on many different kinds of computers. Some computers have different memory spaces. For example, GPUs (Graphics Processing Units) by NVIDIA have "device memory" and "host memory." The GPU has faster access to device memory than host memory, but usually there is less device memory than host memory. Intel's "Knights Landing" architecture has two different memory spaces, also with different capacity and performance characteristics. Some architectures let the processor address memory in any space, possibly with a performance penalty. Others can only access data in certain spaces, and require a special system call to copy memory between spaces.
The Kokkos package provides abstractions for handling multiple memory spaces. In particular, Kokkos::DualView lets users "mirror" data that live in one space, with data in another space. It also lets users manually mark data in one space as modified (modify()), and synchronize (sync()) data from one space to another. The latter only actually copies if the data have been marked as modified. Users can access data in a particular space by calling view(). All three of these methods – modify(), sync(), and view() – are templated on the memory space. This is how users select the memory space on which they want the method to act.
MultiVector implements "DualView semantics." This means that it implements the above three operations:
If your computer only has one memory space, as with conventional single-core or multicore processors, you don't have to worry about this. You can ignore the modify() and sync() methods in that case.
The getLocalView() method for getting a Kokkos::View is the main way to access a MultiVector's local data. If you want to read or write the actual values in a multivector, this is what you want. The resulting Kokkos::View behaves like a 2-D array. You can address it using an index pair (i,j), where i is the local row index, and j is the column index.
MultiVector also has methods that return an Teuchos::ArrayRCP<Scalar> ("1-D view"), or a Teuchos::ArrayRCP<Teuchos::ArrayRCP<Scalar> > ("2-D view"). These exist only for backwards compatibility, and also give access to the local data.
All of these views only view local data. This means that the corresponding rows of the multivector are owned by the calling (MPI) process. You may not use these methods to access remote data, that is, rows that do not belong to the calling process.
MultiVector's public interface also has methods for modifying local data, like sumIntoLocalValue() and replaceGlobalValue(). These methods act on host data only. To access or modify device data, you must get the Kokkos::View and work with it directly.
Tpetra was designed to allow different data representations underneath the same interface. This lets Tpetra run correctly and efficiently on many different kinds of hardware. These different kinds of hardware all have in common the following:
These conclusions have practical consequences for the MultiVector interface. In particular, we have deliberately made it difficult for you to access data directly by raw pointer. This is because the underlying layout may not be what you expect. The memory might not even be accessible from the host CPU. Instead, we give access through a Kokkos::View, which behaves like a 2-D array. You can ask the Kokkos::View for a raw pointer by calling its data() method, but then you are responsible for understanding its layout in memory.
A MultiVector's rows are distributed over processes in its (row) Map's communicator. A MultiVector is a DistObject; the Map of the DistObject tells which process in the communicator owns which rows. This means that you may use Import and Export operations to migrate between different distributions. Please refer to the documentation of Map, Import, and Export for more information.
MultiVector includes methods that perform parallel all-reduces. These include inner products and various kinds of norms. All of these methods have the same blocking semantics as MPI_Allreduce.
Definition at line 385 of file Tpetra_MultiVector_decl.hpp.
| using Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::scalar_type = Scalar |
The type of each entry in the MultiVector.
Definition at line 393 of file Tpetra_MultiVector_decl.hpp.
| using Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::impl_scalar_type = typename Kokkos::Details::ArithTraits<Scalar>::val_type |
The type used internally in place of Scalar.
Some Scalar types might not work with Kokkos on all execution spaces, due to missing CUDA device macros or missing volatile overloads of some methods. The C++ standard type std::complex<T> has this problem. To fix this, we replace std::complex<T> values internally with the bitwise identical type Kokkos::complex<T>. The latter is the impl_scalar_type corresponding to Scalar = std::complex<T>.
Most users don't need to know about this. Just be aware that if you ask for a Kokkos::View or Kokkos::DualView of the MultiVector's data, its entries have type impl_scalar_type, not scalar_type.
Definition at line 410 of file Tpetra_MultiVector_decl.hpp.
| using Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::map_type = Map<LocalOrdinal, GlobalOrdinal, Node> |
The type of the Map specialization used by this class.
Definition at line 413 of file Tpetra_MultiVector_decl.hpp.
| using Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::local_ordinal_type = typename map_type::local_ordinal_type |
The type of local indices that this class uses.
Definition at line 415 of file Tpetra_MultiVector_decl.hpp.
| using Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::global_ordinal_type = typename map_type::global_ordinal_type |
The type of global indices that this class uses.
Definition at line 417 of file Tpetra_MultiVector_decl.hpp.
| using Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::device_type = typename map_type::device_type |
This class' preferred Kokkos device type.
Definition at line 419 of file Tpetra_MultiVector_decl.hpp.
| using Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::node_type = typename map_type::node_type |
Legacy thing that you should not use any more.
Definition at line 421 of file Tpetra_MultiVector_decl.hpp.
| using Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::dot_type = typename Kokkos::Details::InnerProductSpaceTraits<impl_scalar_type>::dot_type |
Type of an inner ("dot") product result.
This is usually the same as impl_scalar_type, but may differ if impl_scalar_type is e.g., an uncertainty quantification type from the Stokhos package.
Definition at line 429 of file Tpetra_MultiVector_decl.hpp.
| using Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::mag_type = typename Kokkos::ArithTraits<impl_scalar_type>::mag_type |
Type of a norm result.
This is usually the same as the type of the magnitude (absolute value) of impl_scalar_type, but may differ if impl_scalar_type is e.g., an uncertainty quantification type from the Stokhos package.
Definition at line 437 of file Tpetra_MultiVector_decl.hpp.
| using Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::execution_space = typename device_type::execution_space |
Type of the (new) Kokkos execution space.
The execution space implements parallel operations, like parallel_for, parallel_reduce, and parallel_scan.
Definition at line 443 of file Tpetra_MultiVector_decl.hpp.
| using Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::dual_view_type = Kokkos::DualView<impl_scalar_type**, Kokkos::LayoutLeft, execution_space> |
Kokkos::DualView specialization used by this class.
This is of interest to users who already have a Kokkos::DualView, and want the MultiVector to view it. By "view" it, we mean that the MultiVector doesn't copy the data in the DualView; it just hangs on to the pointer.
We take particular care to template the DualView on an execution space, rather than a memory space. This ensures that Tpetra will use exactly the specified execution space(s) and no others. This matters because View (and DualView) initialization is a parallel Kokkos kernel. If the View is templated on an execution space, Kokkos uses that execution space (and only that execution space) to initialize the View. This is what we want. If the View is templated on a memory space, Kokkos uses the memory space's default execution space to initialize. This is not necessarily what we want. For example, if building with OpenMP enabled, the default execution space for host memory is Kokkos::OpenMP, even if the user-specified DeviceType is Kokkos::Serial. That is why we go through the trouble of asking for the execution_space's execution space.
Definition at line 469 of file Tpetra_MultiVector_decl.hpp.
|
protected |
Kokkos::Device specialization for communication buffers.
See #1088 for why this is not just device_type::device_type.
Definition at line 2317 of file Tpetra_MultiVector_decl.hpp.
|
inherited |
The type of each datum being sent or received in an Import or Export.
Note that this type does not always correspond to the Scalar template parameter of subclasses.
Definition at line 337 of file Tpetra_DistObject_decl.hpp.
| Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::MultiVector | ( | ) |
Default constructor: makes a MultiVector with no rows or columns.
Definition at line 419 of file Tpetra_MultiVector_def.hpp.
| Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::MultiVector | ( | const Teuchos::RCP< const map_type > & | map, |
| const size_t | numVecs, | ||
| const bool | zeroOut = true |
||
| ) |
Basic constuctor.
| map | [in] Map describing the distribution of rows. |
| numVecs | [in] Number of vectors (columns). |
| zeroOut | [in] Whether to initialize all the entries of the MultiVector to zero. |
Definition at line 425 of file Tpetra_MultiVector_def.hpp.
| Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::MultiVector | ( | const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | source, |
| const Teuchos::DataAccess | copyOrView | ||
| ) |
Copy constructor, with option to do deep or shallow copy.
The current (so-called "Kokkos refactor," circa >= 2014/5) version of Tpetra, unlike the previous "classic" version, always has view semantics. Thus, copyOrView = Teuchos::View has no effect, and copyOrView = Teuchos::Copy does not mark this MultiVector as having copy semantics. However, copyOrView = Teuchos::Copy will make the resulting MultiVector a deep copy of the input MultiVector.
Definition at line 439 of file Tpetra_MultiVector_def.hpp.
| Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::MultiVector | ( | const Teuchos::RCP< const map_type > & | map, |
| const Teuchos::ArrayView< const Scalar > & | A, | ||
| const size_t | LDA, | ||
| const size_t | NumVectors | ||
| ) |
Create multivector by copying two-dimensional array of local data.
| map | [in] The Map describing the distribution of rows of the multivector. |
| view | [in] A view of column-major dense matrix data. The calling process will make a deep copy of this data. |
| LDA | [in] The leading dimension (a.k.a. "stride") of the column-major input data. |
| NumVectors | [in] The number of columns in the input data. This will be the number of vectors in the returned multivector. |
Definition at line 769 of file Tpetra_MultiVector_def.hpp.
| Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::MultiVector | ( | const Teuchos::RCP< const map_type > & | map, |
| const Teuchos::ArrayView< const Teuchos::ArrayView< const Scalar > > & | ArrayOfPtrs, | ||
| const size_t | NumVectors | ||
| ) |
Create multivector by copying array of views of local data.
| map | [in] The Map describing the distribution of rows of the multivector. |
| ArrayOfPtrs | [in/out] Array of views of each column's data. The calling process will make a deep copy of this data. |
| NumVectors | [in] The number of columns in the input data, and the number of elements in ArrayOfPtrs. This will be the number of vectors in the returned multivector. |
Definition at line 840 of file Tpetra_MultiVector_def.hpp.
| Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::MultiVector | ( | const Teuchos::RCP< const map_type > & | map, |
| const dual_view_type & | view | ||
| ) |
Constructor, that takes a Kokkos::DualView of the MultiVector's data, and returns a MultiVector that views those data.
To "view those data" means that this MultiVector and the input Kokkos::DualView point to the same data, just like two "raw" pointers (e.g., double*) can point to the same data. If you modify one, the other sees it (subject to the limitations of cache coherence).
| map | [in] Map describing the distribution of rows. |
| view | [in] Kokkos::DualView of the data to view. |
Definition at line 473 of file Tpetra_MultiVector_def.hpp.
| Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::MultiVector | ( | const Teuchos::RCP< const map_type > & | map, |
| const typename dual_view_type::t_dev & | d_view | ||
| ) |
Constructor, that takes a Kokkos::View of the MultiVector's data (living in the Device's memory space), and returns a MultiVector that views those data.
| map | [in] Map describing the distribution of rows. |
| view | [in] Kokkos::View of the data to view. |
Q: What's the difference between this constructor (that takes a Kokkos::View), and the constructor above that takes a Kokkos::DualView?
A: Suppose that for the MultiVector's device type, there are actually two memory spaces (e.g., for Kokkos::Cuda with UVM off, assuming that this is allowed). In order for MultiVector to implement DualView semantics correctly, this constructor must allocate a Kokkos::View of host memory (or lazily allocate it on modify() or sync()).
Now suppose that you pass in the same Kokkos::View of device memory to two different MultiVector instances, X and Y. Each would allocate its own Kokkos::View of host memory. That means that X and Y would have different DualView instances, but their DualView instances would have the same device View.
Suppose that you do the following:
This would clobber Y's later changes on host, in favor of X's earlier changes on host. That could be very confusing. We allow this behavior because Kokkos::DualView allows it. That is, Kokkos::DualView also lets you get the device View, and hand it off to another Kokkos::DualView. It's confusing, but users need to know what they are doing if they start messing around with multiple memory spaces.
Definition at line 510 of file Tpetra_MultiVector_def.hpp.
| Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::MultiVector | ( | const Teuchos::RCP< const map_type > & | map, |
| const dual_view_type & | view, | ||
| const dual_view_type & | origView | ||
| ) |
Expert mode constructor, that takes a Kokkos::DualView of the MultiVector's data and the "original" Kokkos::DualView of the data, and returns a MultiVector that views those data.
| map | [in] Map describing the distribution of rows. |
| view | [in] View of the data (shallow copy). |
| origView | [in] The original view of the data. |
The original view keeps the "original" dimensions. Doing so lets us safely construct a column Map view of a (domain Map view of a (column Map MultiVector)). The result of a Kokkos::subview does not remember the original dimensions of the view, and does not allow constructing a view with a superset of rows or columns, so we have to keep the original view.
Definition at line 553 of file Tpetra_MultiVector_def.hpp.
|
protected |
Single-column subview constructor, for derived classes ONLY.
| X | [in] Input MultiVector to view (in possibly nonconst fashion). |
| j | [in] The column of X to view. |
Definition at line 3397 of file Tpetra_MultiVector_def.hpp.
| Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::MultiVector | ( | const Teuchos::RCP< const map_type > & | map, |
| const dual_view_type & | view, | ||
| const Teuchos::ArrayView< const size_t > & | whichVectors | ||
| ) |
Expert mode constructor for noncontiguous views.
This constructor takes a Kokkos::DualView for the MultiVector to view, and a list of the columns to view, and returns a MultiVector that views those data. The resulting MultiVector does not have constant stride, that is, isConstantStride() returns false.
| map | [in] Map describing the distribution of rows. |
| view | [in] Device view to the data (shallow copy). |
| whichVectors | [in] Which columns (vectors) to view. |
Definition at line 593 of file Tpetra_MultiVector_def.hpp.
| Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::MultiVector | ( | const Teuchos::RCP< const map_type > & | map, |
| const dual_view_type & | view, | ||
| const dual_view_type & | origView, | ||
| const Teuchos::ArrayView< const size_t > & | whichVectors | ||
| ) |
Expert mode constructor for noncontiguous views, with original view.
This constructor takes a Kokkos::DualView for the MultiVector to view, a view of the "original" data, and a list of the columns to view, and returns a MultiVector that views those data. The resulting MultiVector does not have constant stride, that is, isConstantStride() returns false.
| map | [in] Map describing the distribution of rows. |
| view | [in] View of the data (shallow copy). |
| origView | [in] The original view of the data. |
| whichVectors | [in] Which columns (vectors) to view. |
The original view keeps the "original" dimensions. Doing so lets us safely construct a column Map view of a (domain Map view of a (column Map MultiVector)). The result of a Kokkos::subview does not remember the original dimensions of the view, and does not allow constructing a view with a superset of rows or columns, so we have to keep the original view.
Definition at line 678 of file Tpetra_MultiVector_def.hpp.
| Tpetra::MultiVector< Scalar, LO, GO, Node >::MultiVector | ( | const MultiVector< Scalar, LO, GO, Node > & | X, |
| const Teuchos::RCP< const map_type > & | subMap, | ||
| const local_ordinal_type | rowOffset = 0 |
||
| ) |
"Offset view" constructor; make a view of a contiguous subset of rows on each process.
Return a view of the MultiVector X, which views a subset of the rows of X. Specify the subset by a subset Map of this MultiVector's current row Map, and an optional (local) offset. "View" means "alias": if the original (this) MultiVector's data change, the view will see the changed data.
| X | [in] The MultiVector to view. |
| subMap | [in] The row Map for the new MultiVector. This must be a subset Map of the input MultiVector's row Map. |
| offset | [in] The local row offset at which to start the view. |
Suppose that you have a MultiVector X, and you want to view X, on all processes in X's (MPI) communicator, as split into two row blocks X1 and X2. One could express this in Matlab notation as X = [X1; X2], except that here, X1 and X2 are views into X, rather than copies of X's data. This method assumes that the local indices of X1 and X2 are each contiguous, and that the local indices of X2 follow those of X1. If that is not the case, you cannot use views to divide X into blocks like this; you must instead use the Import or Export functionality, which copies the relevant rows of X.
Here is how you would construct the views X1 and X2.
It is legal, in the above example, for X1 or X2 to have zero local rows on any or all process(es). In that case, the corresponding Map must have zero local entries on that / those process(es). In particular, if X2 has zero local rows on a process, then the corresponding offset on that process would be the number of local rows in X (and therefore in X1) on that process. This is the only case in which the sum of the local number of entries in subMap (in this case, zero) and the offset may equal the number of local entries in *this.
Definition at line 3032 of file Tpetra_MultiVector_def.hpp.
| Tpetra::MultiVector< Scalar, LO, GO, Node >::MultiVector | ( | const MultiVector< Scalar, LO, GO, Node > & | X, |
| const map_type & | subMap, | ||
| const size_t | offset = 0 |
||
| ) |
"Offset view" constructor, that takes the new Map as a const Map& rather than by RCP.
This constructor exists for backwards compatibility. It invokes the input Map's copy constructor, which is a shallow copy. Maps are immutable anyway, so the copy is harmless.
Definition at line 3189 of file Tpetra_MultiVector_def.hpp.
|
default |
Copy constructor (shallow copy).
MultiVector's copy constructor always does a shallow copy. Use the nonmember function Tpetra::deep_copy (see below) to deep-copy one existing MultiVector to another, and use the two-argument "copy constructor" (in this file, with copyOrView=Teuchos::Copy) to create a MultiVector that is a deep copy of an existing MultiVector.
|
default |
Move constructor (shallow move).
|
virtualdefault |
Destructor (virtual for memory safety of derived classes).
=default declarations for copy construction, move construction, copy assignment, and move assignment.
|
default |
Copy assigment (shallow copy).
MultiVector's copy constructor always does a shallow copy. Use the nonmember function Tpetra::deep_copy (see below) to deep-copy one existing MultiVector to another.
|
default |
Move assigment (shallow move).
| void Tpetra::MultiVector< ST, LO, GO, NT >::swap | ( | MultiVector< ST, LO, GO, NT > & | mv | ) |
Swap contents of mv with contents of *this.
Definition at line 4567 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::replaceGlobalValue | ( | const GlobalOrdinal | gblRow, |
| const size_t | col, | ||
| const impl_scalar_type & | value | ||
| ) | const |
Replace value in host memory, using global row index.
Replace the current value at row gblRow (a global index) and column col with the given value. The column index is zero based.
This method affects the host memory version of the data. If device_type is a Kokkos device that has two memory spaces, and you want to modify the non-host version of the data, you must access the device View directly by calling getLocalView(). Please see modify(), sync(), and the discussion of DualView semantics elsewhere in the documentation. You are responsible for calling modify() and sync(), if needed; this method doesn't do that.
This method does not have an "atomic" option like sumIntoGlobalValue. This is deliberate. Replacement is not commutative, unlike += (modulo rounding error). Concurrent calls to replaceGlobalValue on different threads that modify the same entry/ies have undefined results. (It's not just that one thread might win; it's that the value might get messed up.)
| gblRow | [in] Global row index of the entry to modify. This must be a valid global row index on the calling process with respect to the MultiVector's Map. |
| col | [in] Column index of the entry to modify. |
| value | [in] Incoming value to add to the entry. |
Definition at line 4126 of file Tpetra_MultiVector_def.hpp.
|
inline |
Like the above replaceGlobalValue, but only enabled if T differs from impl_scalar_type.
This method only exists if its template parameter T and impl_scalar_type differ, and if it is syntactically possible to convert T to impl_scalar_type. This method is mainly useful for backwards compatibility, when the Scalar template parameter differs from impl_scalar_type. That is commonly only the case when Scalar is std::complex<U> for some type U.
This method affects the host memory version of the data. If device_type is a Kokkos device that has two memory spaces, and you want to modify the non-host version of the data, you must access the device View directly by calling getLocalView(). Please see modify(), sync(), and the discussion of DualView semantics elsewhere in the documentation. You are responsible for calling modify() and sync(), if needed; this method doesn't do that.
This method does not have an "atomic" option like sumIntoGlobalValue. This is deliberate. Replacement is not commutative, unlike += (modulo rounding error). Concurrent calls to replaceGlobalValue on different threads that modify the same entry/ies have undefined results. (It's not just that one thread might win; it's that the value might get messed up.)
| gblRow | [in] Global row index of the entry to modify. This must be a valid global row index on the calling process with respect to the MultiVector's Map. |
| col | [in] Column index of the entry to modify. |
| value | [in] Incoming value to add to the entry. |
Definition at line 881 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::sumIntoGlobalValue | ( | const GlobalOrdinal | gblRow, |
| const size_t | col, | ||
| const impl_scalar_type & | value, | ||
| const bool | atomic = useAtomicUpdatesByDefault |
||
| ) | const |
Update (+=) a value in host memory, using global row index.
Add the given value to the existing value at row gblRow (a global index) and column col. The column index is zero based.
This method affects the host memory version of the data. If device_type is a Kokkos device that has two memory spaces, and you want to modify the non-host version of the data, you must access the device View directly by calling getLocalView(). Please see modify(), sync(), and the discussion of DualView semantics elsewhere in the documentation. You are responsible for calling modify() and sync(), if needed; this method doesn't do that.
| gblRow | [in] Global row index of the entry to modify. This must be a valid global row index on the calling process with respect to the MultiVector's Map. |
| col | [in] Column index of the entry to modify. |
| value | [in] Incoming value to add to the entry. |
| atomic | [in] Whether to use an atomic update. If this class' execution space is not Kokkos::Serial, then this is true by default, else it is false by default. |
Definition at line 4150 of file Tpetra_MultiVector_def.hpp.
|
inline |
Like the above sumIntoGlobalValue, but only enabled if T differs from impl_scalar_type.
This method only exists if its template parameter T and impl_scalar_type differ, and if it is syntactically possible to convert T to impl_scalar_type. This method is mainly useful for backwards compatibility, when the Scalar template parameter differs from impl_scalar_type. That is commonly only the case when Scalar is std::complex<U> for some type U.
This method affects the host memory version of the data. If device_type is a Kokkos device that has two memory spaces, and you want to modify the non-host version of the data, you must access the device View directly by calling getLocalView(). Please see modify(), sync(), and the discussion of DualView semantics elsewhere in the documentation. You are responsible for calling modify() and sync(), if needed; this method doesn't do that.
| gblRow | [in] Global row index of the entry to modify. This must be a valid global row index on the calling process with respect to the MultiVector's Map. |
| col | [in] Column index of the entry to modify. |
| val | [in] Incoming value to add to the entry. |
| atomic | [in] Whether to use an atomic update. If this class' execution space is not Kokkos::Serial, then this is true by default, else it is false by default. |
Definition at line 946 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::replaceLocalValue | ( | const LocalOrdinal | lclRow, |
| const size_t | col, | ||
| const impl_scalar_type & | value | ||
| ) | const |
Replace value in host memory, using local (row) index.
Replace the current value at row lclRow (a local index) and column col with the given value. The column index is zero based.
This method affects the host memory version of the data. If device_type is a Kokkos device that has two memory spaces, and you want to modify the non-host version of the data, you must access the device View directly by calling getLocalView(). Please see modify(), sync(), and the discussion of DualView semantics elsewhere in the documentation. You are responsible for calling modify() and sync(), if needed; this method doesn't do that.
This method does not have an "atomic" option like sumIntoLocalValue. This is deliberate. Replacement is not commutative, unlike += (modulo rounding error). Concurrent calls to replaceLocalValue on different threads that modify the same entry/ies have undefined results. (It's not just that one thread might win; it's that the value might get messed up.)
| lclRow | [in] Local row index of the entry to modify. Must be a valid local index in this MultiVector's Map on the calling process. |
| col | [in] Column index of the entry to modify. |
| value | [in] Incoming value to add to the entry. |
Definition at line 4064 of file Tpetra_MultiVector_def.hpp.
|
inline |
Like the above replaceLocalValue, but only enabled if T differs from impl_scalar_type.
This method only exists if its template parameter T and impl_scalar_type differ, and if it is syntactically possible to convert T to impl_scalar_type. This method is mainly useful for backwards compatibility, when the Scalar template parameter differs from impl_scalar_type. That is commonly only the case when Scalar is std::complex<U> for some type U.
This method affects the host memory version of the data. If device_type is a Kokkos device that has two memory spaces, and you want to modify the non-host version of the data, you must access the device View directly by calling getLocalView(). Please see modify(), sync(), and the discussion of DualView semantics elsewhere in the documentation. You are responsible for calling modify() and sync(), if needed; this method doesn't do that.
This method does not have an "atomic" option like sumIntoLocalValue. This is deliberate. Replacement is not commutative, unlike += (modulo rounding error). Concurrent calls to replaceLocalValue on different threads that modify the same entry/ies have undefined results. (It's not just that one thread might win; it's that the value might get messed up.)
| lclRow | [in] Local row index of the entry to modify. Must be a valid local index in this MultiVector's Map on the calling process. |
| col | [in] Column index of the entry to modify. |
| val | [in] Incoming value to add to the entry. |
Definition at line 1021 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::sumIntoLocalValue | ( | const LocalOrdinal | lclRow, |
| const size_t | col, | ||
| const impl_scalar_type & | val, | ||
| const bool | atomic = useAtomicUpdatesByDefault |
||
| ) | const |
Update (+=) a value in host memory, using local row index.
Add the given value to the existing value at row localRow (a local index) and column col. The column index is zero based.
This method affects the host memory version of the data. If device_type is a Kokkos device that has two memory spaces, and you want to modify the non-host version of the data, you must access the device View directly by calling getLocalView(). Please see modify(), sync(), and the discussion of DualView semantics elsewhere in the documentation. You are responsible for calling modify() and sync(), if needed; this method doesn't do that.
| lclRow | [in] Local row index of the entry to modify. Must be a valid local index in this MultiVector's Map on the calling process. |
| col | [in] Column index of the entry to modify. |
| val | [in] Incoming value to add to the entry. |
| atomic | [in] Whether to use an atomic update. If this class' execution space is not Kokkos::Serial, then this is true by default, else it is false by default. |
Definition at line 4092 of file Tpetra_MultiVector_def.hpp.
|
inline |
Like the above sumIntoLocalValue, but only enabled if T differs from impl_scalar_type.
This method only exists if its template parameter T and impl_scalar_type differ, and if it is syntactically possible to convert T to impl_scalar_type. This method is mainly useful for backwards compatibility, when the Scalar template parameter differs from impl_scalar_type. That is commonly only the case when Scalar is std::complex<U> for some type U.
This method affects the host memory version of the data. If device_type is a Kokkos device that has two memory spaces, and you want to modify the non-host version of the data, you must access the device View directly by calling getLocalView(). Please see modify(), sync(), and the discussion of DualView semantics elsewhere in the documentation. You are responsible for calling modify() and sync(), if needed; this method doesn't do that.
| lclRow | [in] Local row index of the entry to modify. |
| col | [in] Column index of the entry to modify. |
| val | [in] Incoming value to add to the entry. |
| atomic | [in] Whether to use an atomic update. If this class' execution space is not Kokkos::Serial, then this is true by default, else it is false by default. |
Definition at line 1084 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::putScalar | ( | const Scalar & | value | ) |
Set all values in the multivector with the given value.
Definition at line 2317 of file Tpetra_MultiVector_def.hpp.
|
inline |
Set all values in the multivector with the given value.
This method only exists if its template parameter T and impl_scalar_type differ, and if it is syntactically possible to convert T to impl_scalar_type. This method is mainly useful for backwards compatibility, when the Scalar template parameter differs from impl_scalar_type. That is commonly only the case when Scalar is std::complex<U> for some type U.
Definition at line 1105 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::randomize | ( | ) |
Set all values in the multivector to pseudorandom numbers.
Definition at line 2253 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::randomize | ( | const Scalar & | minVal, |
| const Scalar & | maxVal | ||
| ) |
Set all values in the multivector to pseudorandom numbers in the given range.
Definition at line 2270 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::replaceMap | ( | const Teuchos::RCP< const map_type > & | map | ) |
Replace the underlying Map in place.
map->isCompatible (this->getMap ()). "Similar" means that the communicators have the same number of processes, though these need not be in the same order (have the same assignments of ranks) or represent the same communication contexts. It means the same thing as the MPI_SIMILAR return value of MPI_COMM_COMPARE. See MPI 3.0 Standard, Section 6.4.1.This method replaces this object's Map with the given Map. This relabels the rows of the multivector using the global IDs in the input Map. Thus, it implicitly applies a permutation, without actually moving data. If the new Map's communicator has more processes than the original Map's communicator, it "projects" the MultiVector onto the new Map by filling in missing rows with zeros. If the new Map's communicator has fewer processes than the original Map's communicator, the method "forgets about" any rows that do not exist in the new Map. (It mathematical terms, if one considers a MultiVector as a function from one vector space to another, this operation restricts the range.)
This method must always be called collectively on the communicator with the largest number of processes: either this object's current communicator (this->getMap()->getComm()), or the new Map's communicator (map->getComm()). If the new Map's communicator has fewer processes, then the new Map must be null on processes excluded from the original communicator, and the current Map must be nonnull on all processes. If the new Map has more processes, then it must be nonnull on all those processes, and the original Map must be null on those processes which are not in the new Map's communicator. (The latter case can only happen to a MultiVector to which a replaceMap() operation has happened before.)
this->getMap ()->getComm ()). We reserve the right to do checking in debug mode that requires this method to be called collectively in order not to deadlock.Definition at line 2367 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::reduce | ( | ) |
Sum values of a locally replicated multivector across all processes.
Definition at line 4028 of file Tpetra_MultiVector_def.hpp.
| Teuchos::RCP< MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::subCopy | ( | const Teuchos::Range1D & | colRng | ) | const |
Return a MultiVector with copies of selected columns.
Definition at line 3005 of file Tpetra_MultiVector_def.hpp.
| Teuchos::RCP< MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::subCopy | ( | const Teuchos::ArrayView< const size_t > & | cols | ) | const |
Return a MultiVector with copies of selected columns.
Definition at line 2976 of file Tpetra_MultiVector_def.hpp.
| Teuchos::RCP< const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::subView | ( | const Teuchos::Range1D & | colRng | ) | const |
Return a const MultiVector with const views of selected columns.
Definition at line 3267 of file Tpetra_MultiVector_def.hpp.
| Teuchos::RCP< const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::subView | ( | const Teuchos::ArrayView< const size_t > & | cols | ) | const |
Return a const MultiVector with const views of selected columns.
Definition at line 3219 of file Tpetra_MultiVector_def.hpp.
| Teuchos::RCP< MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::subViewNonConst | ( | const Teuchos::Range1D & | colRng | ) |
Return a MultiVector with views of selected columns.
Definition at line 3388 of file Tpetra_MultiVector_def.hpp.
| Teuchos::RCP< MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::subViewNonConst | ( | const Teuchos::ArrayView< const size_t > & | cols | ) |
Return a MultiVector with views of selected columns.
Definition at line 3378 of file Tpetra_MultiVector_def.hpp.
| Teuchos::RCP< const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::offsetView | ( | const Teuchos::RCP< const map_type > & | subMap, |
| const size_t | offset | ||
| ) | const |
Return a const view of a subset of rows.
Return a const (nonmodifiable) view of this MultiVector consisting of a subset of the rows, as specified by an offset and a subset Map of this MultiVector's current row Map. If you want X1 or X2 to be nonconst (modifiable) views, use offsetViewNonConst() with the same arguments. "View" means "alias": if the original (this) MultiVector's data change, the view will see the changed data.
| subMap | [in] The row Map for the new MultiVector. This must be a subset Map of this MultiVector's row Map. |
| offset | [in] The local row offset at which to start the view. |
Suppose that you have a MultiVector X, and you want to view X, on all processes in X's (MPI) communicator, as split into two row blocks X1 and X2. One could express this in Matlab notation as X = [X1; X2], except that here, X1 and X2 are views into X, rather than copies of X's data. This method assumes that the local indices of X1 and X2 are each contiguous, and that the local indices of X2 follow those of X1. If that is not the case, you cannot use views to divide X into blocks like this; you must instead use the Import or Export functionality, which copies the relevant rows of X.
Here is how you would construct the views X1 and X2.
It is legal, in the above example, for X1 or X2 to have zero local rows on any or all process(es). In that case, the corresponding Map must have zero local entries on that / those process(es). In particular, if X2 has zero local rows on a process, then the corresponding offset on that process would be the number of local rows in X (and therefore in X1) on that process. This is the only case in which the sum of the local number of entries in subMap (in this case, zero) and the offset may equal the number of local entries in *this.
Definition at line 3199 of file Tpetra_MultiVector_def.hpp.
| Teuchos::RCP< MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::offsetViewNonConst | ( | const Teuchos::RCP< const map_type > & | subMap, |
| const size_t | offset | ||
| ) |
Return a nonconst view of a subset of rows.
Return a nonconst (modifiable) view of this MultiVector consisting of a subset of the rows, as specified by an offset and a subset Map of this MultiVector's current row Map. If you want X1 or X2 to be const (nonmodifiable) views, use offsetView() with the same arguments. "View" means "alias": if the original (this) MultiVector's data change, the view will see the changed data, and if the view's data change, the original MultiVector will see the changed data.
| subMap | [in] The row Map for the new MultiVector. This must be a subset Map of this MultiVector's row Map. |
| offset | [in] The local row offset at which to start the view. |
See the documentation of offsetView() for a code example and an explanation of edge cases.
Definition at line 3209 of file Tpetra_MultiVector_def.hpp.
| Teuchos::RCP< const Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getVector | ( | const size_t | j | ) | const |
Return a Vector which is a const view of column j.
Definition at line 3454 of file Tpetra_MultiVector_def.hpp.
| Teuchos::RCP< Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getVectorNonConst | ( | const size_t | j | ) |
Return a Vector which is a nonconst view of column j.
Definition at line 3464 of file Tpetra_MultiVector_def.hpp.
| Teuchos::ArrayRCP< const Scalar > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getData | ( | size_t | j | ) | const |
Const view of the local values in a particular vector of this multivector.
Definition at line 2908 of file Tpetra_MultiVector_def.hpp.
| Teuchos::ArrayRCP< Scalar > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getDataNonConst | ( | size_t | j | ) |
View of the local values in a particular vector of this multivector.
Definition at line 2940 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::get1dCopy | ( | const Teuchos::ArrayView< Scalar > & | A, |
| const size_t | LDA | ||
| ) | const |
Fill the given array with a copy of this multivector's local values.
| A | [out] View of the array to fill. We consider A as a matrix with column-major storage. |
| LDA | [in] Leading dimension of the matrix A. |
Definition at line 3474 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::get2dCopy | ( | const Teuchos::ArrayView< const Teuchos::ArrayView< Scalar > > & | ArrayOfPtrs | ) | const |
Fill the given array with a copy of this multivector's local values.
| ArrayOfPtrs | [out] Array of arrays, one for each column of the multivector. On output, we fill ArrayOfPtrs[j] with the data for column j of this multivector. |
Definition at line 3549 of file Tpetra_MultiVector_def.hpp.
| Teuchos::ArrayRCP< const Scalar > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::get1dView | ( | ) | const |
Const persisting (1-D) view of this multivector's local values.
This method assumes that the columns of the multivector are stored contiguously. If not, this method throws std::runtime_error.
Definition at line 3606 of file Tpetra_MultiVector_def.hpp.
| Teuchos::ArrayRCP< Teuchos::ArrayRCP< const Scalar > > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::get2dView | ( | ) | const |
Return const persisting pointers to values.
Definition at line 3683 of file Tpetra_MultiVector_def.hpp.
| Teuchos::ArrayRCP< Scalar > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::get1dViewNonConst | ( | ) |
Nonconst persisting (1-D) view of this multivector's local values.
This method assumes that the columns of the multivector are stored contiguously. If not, this method throws std::runtime_error.
Definition at line 3633 of file Tpetra_MultiVector_def.hpp.
| Teuchos::ArrayRCP< Teuchos::ArrayRCP< Scalar > > Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::get2dViewNonConst | ( | ) |
Return non-const persisting pointers to values.
Definition at line 3656 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::clear_sync_state | ( | ) |
Clear "modified" flags on both host and device sides.
Definition at line 4194 of file Tpetra_MultiVector_def.hpp.
|
inline |
Update data on device or host only if data in the other space has been marked as modified.
If TargetDeviceType is the same as this MultiVector's device type, then copy data from host to device. Otherwise, copy data from device to host. In either case, only copy if the source of the copy has been modified.
This is a one-way synchronization only. If the target of the copy has been modified, this operation will discard those modifications. It will also reset both device and host modified flags.
Definition at line 1431 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::sync_host | ( | ) |
Synchronize to Host.
Definition at line 4201 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::sync_device | ( | ) |
Synchronize to Device.
Definition at line 4219 of file Tpetra_MultiVector_def.hpp.
|
inline |
Whether this MultiVector needs synchronization to the given space.
Definition at line 1443 of file Tpetra_MultiVector_decl.hpp.
| bool Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::need_sync_host | ( | ) | const |
Whether this MultiVector needs synchronization to the host.
Definition at line 4226 of file Tpetra_MultiVector_def.hpp.
| bool Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::need_sync_device | ( | ) | const |
Whether this MultiVector needs synchronization to the device.
Definition at line 4233 of file Tpetra_MultiVector_def.hpp.
|
inline |
Mark data as modified on the given device TargetDeviceType.
If TargetDeviceType is the same as this MultiVector's device type, then mark the device's data as modified. Otherwise, mark the host's data as modified.
Definition at line 1459 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::modify_device | ( | ) |
Mark data as modified on the device side.
Definition at line 4240 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::modify_host | ( | ) |
Mark data as modified on the host side.
Definition at line 4247 of file Tpetra_MultiVector_def.hpp.
|
inline |
Return a view of the local data on a specific device.
| TargetDeviceType | The Kokkos Device type whose data to return. |
Please don't be afraid of the if_c expression in the return value's type. That just tells the method what the return type should be: dual_view_type::t_dev if the TargetDeviceType template parameter matches this Tpetra object's device type, else dual_view_type::t_host.
For example, suppose you create a Tpetra::MultiVector for the Kokkos::Cuda device, like this:
If you want to get the CUDA device Kokkos::View, do this:
and if you want to get the host mirror of that View, do this:
Definition at line 1507 of file Tpetra_MultiVector_decl.hpp.
| MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::dual_view_type::t_host Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getLocalViewHost | ( | ) | const |
A local Kokkos::View of host memory.
Definition at line 4261 of file Tpetra_MultiVector_def.hpp.
| MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::dual_view_type::t_dev Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getLocalViewDevice | ( | ) | const |
A local Kokkos::View of device memory.
Definition at line 4254 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::dot | ( | const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | A, |
| const Teuchos::ArrayView< dot_type > & | dots | ||
| ) | const |
Compute the dot product of each corresponding pair of vectors (columns) in A and B.
The "dot product" is the standard Euclidean inner product. If the type of entries of the vectors (impl_scalar_type) is complex, then A is transposed, not *this. For example, if x and y each have one column, then x.dot (y, dots) computes 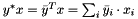 .
.
*this and A have the same number of columns (vectors). dots has at least as many entries as the number of columns in A.dots[j] == (this->getVector[j])->dot (* (A.getVector[j])) Definition at line 2024 of file Tpetra_MultiVector_def.hpp.
|
inline |
Compute the dot product of each corresponding pair of vectors (columns) in A and B.
| T | The output type of the dot products. |
This method only exists if dot_type and T are different types. For example, if impl_scalar_type and dot_type differ, then this method ensures backwards compatibility with the previous interface (that returned dot products as impl_scalar_type rather than as dot_type). The complicated enable_if expression just ensures that the method only exists if dot_type and T are different types; the method still returns void, as above.
Definition at line 1551 of file Tpetra_MultiVector_decl.hpp.
|
inline |
Like the above dot() overload, but for std::vector output.
Definition at line 1566 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::dot | ( | const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | A, |
| const Kokkos::View< dot_type *, Kokkos::HostSpace > & | norms | ||
| ) | const |
Compute the dot product of each corresponding pair of vectors (columns) in A and B, storing the result in a device View.
The "dot product" is the standard Euclidean inner product. If the type of entries of the vectors (impl_scalar_type) is complex, then A is transposed, not *this. For example, if x and y each have one column, then x.dot (y, dots) computes 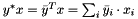 .
.
| A | [in] MultiVector with which to dot *this. |
| dots | [out] Device View with getNumVectors() entries. |
this->getNumVectors () == A.getNumVectors () dots.extent (0) == A.getNumVectors ()dots(j) == (this->getVector[j])->dot (* (A.getVector[j])) Definition at line 1884 of file Tpetra_MultiVector_def.hpp.
|
inline |
Compute the dot product of each corresponding pair of vectors (columns) in A and B, storing the result in a device view.
| T | The output type of the dot products. |
This method only exists if dot_type and T are different types. For example, if Scalar and dot_type differ, then this method ensures backwards compatibility with the previous interface (that returned dot products as Scalar rather than as dot_type). The complicated enable_if expression just ensures that the method only exists if dot_type and T are different types; the method still returns void, as above.
Definition at line 1624 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::abs | ( | const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | A | ) |
Put element-wise absolute values of input Multi-vector in target: A = abs(this)
Definition at line 2720 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::reciprocal | ( | const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | A | ) |
Put element-wise reciprocal values of input Multi-vector in target, this(i,j) = 1/A(i,j).
Definition at line 2671 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::scale | ( | const Scalar & | alpha | ) |
Scale in place: this = alpha*this.
Replace this MultiVector with alpha times this MultiVector. This method will always multiply, even if alpha is zero. That means, for example, that if *this contains NaN entries before calling this method, the NaN entries will remain after this method finishes.
Definition at line 2464 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::scale | ( | const Teuchos::ArrayView< const Scalar > & | alpha | ) |
Scale each column in place: this[j] = alpha[j]*this[j].
Replace each column j of this MultiVector with alpha[j] times the current column j of this MultiVector. This method will always multiply, even if all the entries of alpha are zero. That means, for example, that if *this contains NaN entries before calling this method, the NaN entries will remain after this method finishes.
Definition at line 2517 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::scale | ( | const Kokkos::View< const impl_scalar_type *, device_type > & | alpha | ) |
Scale each column in place: this[j] = alpha[j]*this[j].
Replace each column j of this MultiVector with alpha[j] times the current column j of this MultiVector. This method will always multiply, even if all the entries of alpha are zero. That means, for example, that if *this contains NaN entries before calling this method, the NaN entries will remain after this method finishes.
Definition at line 2541 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::scale | ( | const Scalar & | alpha, |
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | A | ||
| ) |
Scale in place: this = alpha * A.
Replace this MultiVector with scaled values of A. This method will always multiply, even if alpha is zero. That means, for example, that if *this contains NaN entries before calling this method, the NaN entries will remain after this method finishes. It is legal for the input A to alias this MultiVector.
Definition at line 2612 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::update | ( | const Scalar & | alpha, |
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | A, | ||
| const Scalar & | beta | ||
| ) |
Update: this = beta*this + alpha*A.
Update this MultiVector with scaled values of A. If beta is zero, overwrite *this unconditionally, even if it contains NaN entries. It is legal for the input A to alias this MultiVector.
Definition at line 2769 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::update | ( | const Scalar & | alpha, |
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | A, | ||
| const Scalar & | beta, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | B, | ||
| const Scalar & | gamma | ||
| ) |
Update: this = gamma*this + alpha*A + beta*B.
Update this MultiVector with scaled values of A and B. If gamma is zero, overwrite *this unconditionally, even if it contains NaN entries. It is legal for the inputs A or B to alias this MultiVector.
Definition at line 2831 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::norm1 | ( | const Kokkos::View< mag_type *, Kokkos::HostSpace > & | norms | ) | const |
Compute the one-norm of each vector (column), storing the result in a host view.
| norms | [out] Host View with getNumVectors() entries. |
norms.extent (0) == this->getNumVectors () norms(j) == (this->getVector[j])->norm1 (* (A.getVector[j]))The one-norm of a vector is the sum of the magnitudes of the vector's entries. On exit, norms(j) is the one-norm of column j of this MultiVector.
Definition at line 2111 of file Tpetra_MultiVector_def.hpp.
|
inline |
Compute the one-norm of each vector (column), storing the result in a device view.
| T | The output type of the dot products. |
See the above norm1() method for documentation.
This method only exists if mag_type and T are different types. For example, if Teuchos::ScalarTraits<Scalar>::magnitudeType and mag_type differ, then this method ensures backwards compatibility with the previous interface (that returned norms products as Teuchos::ScalarTraits<Scalar>::magnitudeType rather than as mag_type). The complicated enable_if expression just ensures that the method only exists if mag_type and T are different types; the method still returns void, as above.
Definition at line 1756 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::norm1 | ( | const Teuchos::ArrayView< mag_type > & | norms | ) | const |
Compute the one-norm of each vector (column).
See the uppermost norm1() method above for documentation.
Definition at line 2096 of file Tpetra_MultiVector_def.hpp.
|
inline |
Compute the one-norm of each vector (column).
| T | The output type of the norms. |
See the uppermost norm1() method above for documentation.
This method only exists if mag_type and T are different types. For example, if Teuchos::ScalarTraits<Scalar>::magnitudeType and mag_type differ, then this method ensures backwards compatibility with the previous interface (that returned norms as Teuchos::ScalarTraits<Scalar>::magnitudeType rather than as mag_type). The complicated enable_if expression just ensures that the method only exists if mag_type and T are different types; the method still returns void, as above.
Definition at line 1791 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::norm2 | ( | const Kokkos::View< mag_type *, Kokkos::HostSpace > & | norms | ) | const |
Compute the two-norm of each vector (column), storing the result in a host View.
| norms | [out] Host View with getNumVectors() entries. |
norms.extent (0) == this->getNumVectors () norms(j) == (this->getVector[j])->dot (* (A.getVector[j]))The two-norm of a vector is the standard Euclidean norm, the square root of the sum of squares of the magnitudes of the vector's entries. On exit, norms(k) is the two-norm of column k of this MultiVector.
Definition at line 2086 of file Tpetra_MultiVector_def.hpp.
|
inline |
Compute the two-norm of each vector (column), storing the result in a device view.
See the above norm2() method for documentation.
This method only exists if mag_type and T are different types. For example, if Teuchos::ScalarTraits<Scalar>::magnitudeType and mag_type differ, then this method ensures backwards compatibility with the previous interface (that returned norms as Teuchos::ScalarTraits<Scalar>::magnitudeType rather than as mag_type). The complicated enable_if expression just ensures that the method only exists if mag_type and T are different types; the method still returns void, as above.
Definition at line 1846 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::norm2 | ( | const Teuchos::ArrayView< mag_type > & | norms | ) | const |
Compute the two-norm of each vector (column).
See the uppermost norm2() method above for documentation.
Definition at line 2071 of file Tpetra_MultiVector_def.hpp.
|
inline |
Compute the two-norm of each vector (column).
| T | The output type of the norms. |
See the uppermost norm2() method above for documentation.
This method only exists if mag_type and T are different types. For example, if Teuchos::ScalarTraits<Scalar>::magnitudeType and mag_type differ, then this method ensures backwards compatibility with the previous interface (that returned norms products as Teuchos::ScalarTraits<Scalar>::magnitudeType rather than as mag_type). The complicated enable_if expression just ensures that the method only exists if mag_type and T are different types; the method still returns void, as above.
Definition at line 1881 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::normInf | ( | const Kokkos::View< mag_type *, Kokkos::HostSpace > & | norms | ) | const |
Compute the infinity-norm of each vector (column), storing the result in a host View.
The infinity-norm of a vector is the maximum of the magnitudes of the vector's entries. On exit, norms(j) is the infinity-norm of column j of this MultiVector.
Definition at line 2135 of file Tpetra_MultiVector_def.hpp.
|
inline |
Compute the infinity-norm of each vector (column), storing the result in a device view.
See the above normInf() method for documentation.
This method only exists if mag_type and T are different types. For example, if Teuchos::ScalarTraits<Scalar>::magnitudeType and mag_type differ, then this method ensures backwards compatibility with the previous interface (that returned norms as Teuchos::ScalarTraits<Scalar>::magnitudeType rather than as mag_type). The complicated enable_if expression just ensures that the method only exists if mag_type and T are different types; the method still returns void, as above.
Definition at line 1929 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::normInf | ( | const Teuchos::ArrayView< mag_type > & | norms | ) | const |
Compute the infinity-norm of each vector (column), storing the result in a Teuchos::ArrayView.
See the uppermost normInf() method above for documentation.
Definition at line 2120 of file Tpetra_MultiVector_def.hpp.
|
inline |
Compute the infinity-norm of each vector (column), storing the result in a Teuchos::ArrayView.
| T | The output type of the norms. |
See the uppermost normInf() method above for documentation.
This method only exists if mag_type and T are different types. For example, if Teuchos::ScalarTraits<Scalar>::magnitudeType and mag_type differ, then this method ensures backwards compatibility with the previous interface (that returned norms products as Teuchos::ScalarTraits<Scalar>::magnitudeType rather than as mag_type). The complicated enable_if expression just ensures that the method only exists if mag_type and T are different types; the method still returns void, as above.
Definition at line 1966 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::meanValue | ( | const Teuchos::ArrayView< impl_scalar_type > & | means | ) | const |
Compute mean (average) value of each column.
The outcome of this routine is undefined for non-floating point scalar types (e.g., int).
Definition at line 2144 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::multiply | ( | Teuchos::ETransp | transA, |
| Teuchos::ETransp | transB, | ||
| const Scalar & | alpha, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | A, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | B, | ||
| const Scalar & | beta | ||
| ) |
Matrix-matrix multiplication: this = beta*this + alpha*op(A)*op(B).
If beta is zero, overwrite *this unconditionally, even if it contains NaN entries. This imitates the semantics of analogous BLAS routines like DGEMM.
Definition at line 3714 of file Tpetra_MultiVector_def.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::elementWiseMultiply | ( | Scalar | scalarAB, |
| const Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | A, | ||
| const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | B, | ||
| Scalar | scalarThis | ||
| ) |
Multiply a Vector A elementwise by a MultiVector B.
Compute this = scalarThis * this + scalarAB * B @ A where </tt> denotes element-wise multiplication. In pseudocode, if C denotes *this MultiVector:
for all rows i and columns j of C.
B must have the same dimensions as *this, while A must have the same number of rows but a single column.
We do not require that A, B, and *this have compatible Maps, as long as the number of rows in A, B, and *this on each process is the same. For example, one or more of these vectors might have a locally replicated Map, or a Map with a local communicator (MPI_COMM_SELF). This case may occur in block relaxation algorithms when applying a diagonal scaling.
Definition at line 3962 of file Tpetra_MultiVector_def.hpp.
| size_t Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getNumVectors | ( | ) | const |
Number of columns in the multivector.
Definition at line 1820 of file Tpetra_MultiVector_def.hpp.
| size_t Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getLocalLength | ( | ) | const |
Local number of rows on the calling process.
Definition at line 898 of file Tpetra_MultiVector_def.hpp.
| global_size_t Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getGlobalLength | ( | ) | const |
Global number of rows in the multivector.
Definition at line 910 of file Tpetra_MultiVector_def.hpp.
| size_t Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::getStride | ( | ) | const |
Stride between columns in the multivector.
This is only meaningful if isConstantStride() returns true.
Definition at line 922 of file Tpetra_MultiVector_def.hpp.
| bool Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::isConstantStride | ( | ) | const |
Whether this multivector has constant stride between columns.
Definition at line 891 of file Tpetra_MultiVector_def.hpp.
|
virtual |
A simple one-line description of this object.
Reimplemented from Tpetra::DistObject< Scalar, LocalOrdinal, GlobalOrdinal, Node >.
Reimplemented in Tpetra::Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node >.
Definition at line 4298 of file Tpetra_MultiVector_def.hpp.
|
virtual |
Print the object with the given verbosity level to a FancyOStream.
| out | [out] Output stream to which to print. For verbosity levels VERB_LOW and lower, only the process with rank 0 ("Proc 0") in the MultiVector's communicator prints. For verbosity levels strictly higher than VERB_LOW, all processes in the communicator need to be able to print to the output stream. |
| verbLevel | [in] Verbosity level. The default verbosity (verbLevel=VERB_DEFAULT) is VERB_LOW. |
The amount and content of what this method prints depends on the verbosity level. In the list below, each higher level includes all the content of the previous levels, as well as its own content.
description().isConstantStride()), and if so, what that stride is. (Stride may differ on different processes.)Reimplemented from Tpetra::DistObject< Scalar, LocalOrdinal, GlobalOrdinal, Node >.
Reimplemented in Tpetra::Vector< Scalar, LocalOrdinal, GlobalOrdinal, Node >.
Definition at line 4474 of file Tpetra_MultiVector_def.hpp.
|
virtual |
Remove processes owning zero rows from the Map and their communicator.
| newMap | [in] This must be the result of calling the removeEmptyProcesses() method on the row Map. If it is not, this method's behavior is undefined. This pointer will be null on excluded processes. |
Definition at line 4483 of file Tpetra_MultiVector_def.hpp.
|
inline |
Set whether this has copy (copyOrView = Teuchos::Copy) or view (copyOrView = Teuchos::View) semantics.
Definition at line 2130 of file Tpetra_MultiVector_decl.hpp.
|
inline |
Get whether this has copy (copyOrView = Teuchos::Copy) or view (copyOrView = Teuchos::View) semantics.
Definition at line 2147 of file Tpetra_MultiVector_decl.hpp.
| void Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::assign | ( | const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | src | ) |
Copy the contents of src into *this (deep copy).
| src | [in] Source MultiVector (input of the deep copy). |
! src.getMap ().is_null () && ! this->getMap ().is_null () src.getMap ()->isCompatible (* (this->getMap ()) src or *this remain valid.*this, or otherwise change its dimensions. This is not an assignment operator; it does not change anything in *this other than the contents of storage. Definition at line 4491 of file Tpetra_MultiVector_def.hpp.
| bool Tpetra::MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node >::isSameSize | ( | const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > & | vec | ) | const |
| src | [in] MultiVector |
! vec.getMap ().is_null () && ! this->getMap ().is_null () vec.getMap ()->isCompatible (* (this->getMap ()) src or *this remain valid. Definition at line 4541 of file Tpetra_MultiVector_def.hpp.
|
protected |
Implementation of description() for this class, and its subclass Vector.
| className | [in] Name of the class calling this method: Either "Tpetra::MultiVector" or "Tpetra::Vector" (no quotes in the string, in either case). |
Definition at line 4268 of file Tpetra_MultiVector_def.hpp.
|
protected |
Print the calling process' verbose describe() information to the returned string.
This is an implementation detail of describe().
| vl | [in] Verbosity level with which to print. |
Definition at line 4306 of file Tpetra_MultiVector_def.hpp.
|
protected |
Implementation of describe() for this class, and its subclass Vector.
| out | [out] Output stream to which to write. Only Process 0 in this object's communicator may write to the output stream. |
| className | [in] Name of the class calling this method. |
| verbLevel | [in] Verbosity level. This also controls whether this method does any communication. At verbosity levels higher (greater) than Teuchos::VERB_LOW, this method behaves as a collective over the object's communicator. |
Definition at line 4401 of file Tpetra_MultiVector_def.hpp.
|
protected |
Persisting view of j-th column in the given ArrayRCP.
This method considers isConstantStride(). The ArrayRCP may correspond either to a compute buffer or a host view.
Definition at line 4178 of file Tpetra_MultiVector_def.hpp.
|
protected |
"Original" number of rows in the (local) data.
Definition at line 3019 of file Tpetra_MultiVector_def.hpp.
|
protected |
"Original" number of columns in the (local) data.
Definition at line 3026 of file Tpetra_MultiVector_def.hpp.
|
protectedvirtual |
Whether data redistribution between sourceObj and this object is legal.
This method is called in DistObject::doTransfer() to check whether data redistribution between the two objects is legal.
Implements Tpetra::DistObject< Scalar, LocalOrdinal, GlobalOrdinal, Node >.
Definition at line 930 of file Tpetra_MultiVector_def.hpp.
|
protectedvirtual |
Number of packets to send per LID.
Reimplemented from Tpetra::DistObject< Scalar, LocalOrdinal, GlobalOrdinal, Node >.
Definition at line 954 of file Tpetra_MultiVector_def.hpp.
|
inherited |
Import data into this object using an Import object ("forward mode").
The input DistObject is always the source of the data redistribution operation, and the *this object is always the target.
If you don't know the difference between forward and reverse mode, then you probably want forward mode. Use this method with your precomputed Import object if you want to do an Import, else use doExport() with a precomputed Export object.
"Restricted Mode" does two things:
*this, in a "locallyFitted" sense. This cannot be used if (2) is not true, OR there are permutes. The "source" maps still need to match.
| source | [in] The "source" object for redistribution. |
| importer | [in] Precomputed data redistribution plan. Its source Map must be the same as the input DistObject's Map, and its target Map must be the same as this->getMap(). |
| CM | [in] How to combine incoming data with the same global index. |
|
inherited |
Import data into this object using an Export object ("reverse mode").
The input DistObject is always the source of the data redistribution operation, and the *this object is always the target.
If you don't know the difference between forward and reverse mode, then you probably want forward mode. Use the version of doImport() that takes a precomputed Import object in that case.
"Restricted Mode" does two things:
*this, in a "locallyFitted" sense. This cannot be used if (2) is not true, OR there are permutes. The "source" maps still need to match.
| source | [in] The "source" object for redistribution. |
| exporter | [in] Precomputed data redistribution plan. Its target Map must be the same as the input DistObject's Map, and its source Map must be the same as this->getMap(). (Note the difference from forward mode.) |
| CM | [in] How to combine incoming data with the same global index. |
|
inherited |
Export data into this object using an Export object ("forward mode").
The input DistObject is always the source of the data redistribution operation, and the *this object is always the target.
If you don't know the difference between forward and reverse mode, then you probably want forward mode. Use this method with your precomputed Export object if you want to do an Export, else use doImport() with a precomputed Import object.
"Restricted Mode" does two things:
*this, in a "locallyFitted" sense. This cannot be used if (2) is not true, OR there are permutes. The "source" maps still need to match.
| source | [in] The "source" object for redistribution. |
| exporter | [in] Precomputed data redistribution plan. Its source Map must be the same as the input DistObject's Map, and its target Map must be the same as this->getMap(). |
| CM | [in] How to combine incoming data with the same global index. |
|
inherited |
Export data into this object using an Import object ("reverse mode").
The input DistObject is always the source of the data redistribution operation, and the *this object is always the target.
If you don't know the difference between forward and reverse mode, then you probably want forward mode. Use the version of doExport() that takes a precomputed Export object in that case.
"Restricted Mode" does two things:
*this, in a "locallyFitted" sense. This cannot be used if (2) is not true, OR there are permutes. The "source" maps still need to match.
| source | [in] The "source" object for redistribution. |
| importer | [in] Precomputed data redistribution plan. Its target Map must be the same as the input DistObject's Map, and its source Map must be the same as this->getMap(). (Note the difference from forward mode.) |
| CM | [in] How to combine incoming data with the same global index. |
|
inherited |
Whether this is a globally distributed object.
For a definition of "globally distributed" (and its opposite, "locally replicated"), see the documentation of Map's isDistributed() method.
|
inlinevirtualinherited |
The Map describing the parallel distribution of this object.
Note that some Tpetra objects might be distributed using multiple Map objects. For example, CrsMatrix has both a row Map and a column Map. It is up to the subclass to decide which Map to use when invoking the DistObject constructor.
Definition at line 540 of file Tpetra_DistObject_decl.hpp.
|
inherited |
Print this object to the given output stream.
We generally assume that all MPI processes can print to the given stream.
|
virtualinherited |
Remove processes which contain no entries in this object's Map.
On input, this object is distributed over the Map returned by getMap() (the "original Map," with its communicator, the "original communicator"). The input newMap of this method must be the same as the result of calling getMap()->removeEmptyProcesses(). On processes in the original communicator which contain zero entries ("excluded processes," as opposed to "included processes"), the input newMap must be Teuchos::null (which is what getMap()->removeEmptyProcesses() returns anyway).
On included processes, reassign this object's Map (that would be returned by getMap()) to the input newMap, and do any work that needs to be done to restore correct semantics. On excluded processes, free any data that needs freeing, and do any other work that needs to be done to restore correct semantics.
This method has collective semantics over the original communicator. On exit, the only method of this object which is safe to call on excluded processes is the destructor. This implies that subclasses' destructors must not contain communication operations.
|
protectedvirtualinherited |
Redistribute data across (MPI) processes.
| src | [in] The source object, to redistribute into the target object, which is *this object. |
| transfer | [in] The Export or Import object representing the communication pattern. (Details::Transfer is the common base class of these two objects.) |
| modeString | [in] Human-readable string, for verbose debugging output and error output, explaining what function called this method. Example: "doImport (forward)", "doExport (reverse)". |
| revOp | [in] Whether to do a forward or reverse mode redistribution. |
| CM | [in] The combine mode that describes how to combine values that map to the same global ID on the same process. |
|
protectedvirtualinherited |
Reallocate numExportPacketsPerLID_ and/or numImportPacketsPerLID_, if necessary.
| numExportLIDs | [in] Number of entries in the exportLIDs input array argument of doTransfer(). |
| numImportLIDs | [in] Number of entries in the remoteLIDs input array argument of doTransfer(). |
|
protectedvirtualinherited |
Implementation detail of doTransfer.
LID DualViews come from the Transfer object given to doTransfer. They are always sync'd on both host and device. Users must never attempt to modify or sync them.
|
protectedvirtualinherited |
Perform copies and permutations that are local to the calling (MPI) process.
Subclasses must reimplement this function. Its default implementation does nothing. Note that the <t>target object of the Export or Import, namely *this, packs the source object's data.
permuteToLIDs.need_sync_host(), permuteToLIDs.need_sync_device(), permuteFromLIDs.need_sync_host(), and permuteFromLIDs.need_sync_device() are all false.| source | [in] On entry, the source object of the Export or Import operation. |
| numSameIDs | [in] The number of elements that are the same on the source and target objects. These elements live on the same process in both the source and target objects. |
| permuteToLIDs | [in] List of the elements that are permuted. They are listed by their local index (LID) in the destination object. |
| permuteFromLIDs | [in] List of the elements that are permuted. They are listed by their local index (LID) in the source object. |
|
protectedvirtualinherited |
Pack data and metadata for communication (sends).
Subclasses must reimplement this function. Its default implementation does nothing. Note that the <t>target object of the Export or Import, namely *this, packs the source object's data.
exportLIDs.need_sync_host () and exportLIDs.need_sync_device() are both false.| source | [in] Source object for the redistribution. |
| exportLIDs | [in] List of the entries (as local IDs in the source object) that Tpetra will send to other processes. |
| exports | [out] On exit, the packed data to send. Implementations must reallocate this as needed (prefer reusing the existing allocation if possible), and may modify and/or sync this wherever they like. |
| numPacketsPerLID | [out] On exit, the implementation of this method must do one of two things: either set numPacketsPerLID[i] to the number of packets to be packed for exportLIDs[i] and set constantNumPackets to zero, or set constantNumPackets to a nonzero value. If the latter, the implementation must not modify the entries of numPacketsPerLID. If the former, the implementation may sync numPacketsPerLID this wherever it likes, either to host or to device. The allocation belongs to DistObject, not to subclasses; don't be tempted to change this to pass by reference. |
| constantNumPackets | [out] On exit, 0 if the number of packets per LID could differ, else (if nonzero) the number of packets per LID (which must be constant). |
| distor | [in] The Distributor object we are using. Most implementations will not use this. |
|
protectedvirtualinherited |
Perform any unpacking and combining after communication.
Subclasses must reimplement this function. Its default implementation does nothing. Note that the <t>target object of the Export or Import, namely *this, unpacks the received data into itself, possibly modifying its entries.
importLIDs.need_sync_host () and importLIDs.need_sync_device() are both false.| importLIDs | [in] List of the entries (as LIDs in the destination object) we received from other processes. |
| imports | [in/out] On input: Buffer of received data to unpack. DistObject promises nothing about where this is sync'd. Implementations may sync this wherever they like, either to host or to device. The allocation belongs to DistObject, not to subclasses; don't be tempted to change this to pass by reference. |
| numPacketsPerLID | [in/out] On input: If constantNumPackets is zero, then numPacketsPerLID[i] contains the number of packets imported for importLIDs[i]. DistObject promises nothing about where this is sync'd. Implementations may sync this wherever they like, either to host or to device. The allocation belongs to DistObject, not to subclasses; don't be tempted to change this to pass by reference. |
| constantNumPackets | [in] If nonzero, then the number of packets per LID is the same for all entries ("constant") and constantNumPackets is that number. If zero, then numPacketsPerLID[i] is the number of packets to unpack for LID importLIDs[i]. |
| distor | [in] The Distributor object we are using. Most implementations will not use this. |
| combineMode | [in] The CombineMode to use when combining the imported entries with existing entries. |
|
protectedinherited |
Reallocate imports_ if needed.
This unfortunately must be declared protected, for the same reason that imports_ is declared protected.
| newSize | [in] New size of imports_. |
| verbose | [in] Whether to print verbose debugging output to stderr on every (MPI) process in the communicator. |
| prefix | [in] If verbose is true, then this is a nonnull prefix to print at the beginning of each line of verbose debugging output. Otherwise, not used. |
We don't need a "reallocExportsIfNeeded" method, because exports_ always gets passed into packAndPrepare() by nonconst reference. Thus, that method can resize the DualView without needing to call other DistObject methods.
|
related |
Copy the contents of the MultiVector src into dst.
src must be compatible with the Map of dst. Copy the contents of the MultiVector src into the MultiVector dst. ("Copy the contents" means the same thing as "deep
copy.") The two MultiVectors need not necessarily have the same template parameters, but the assignment of their entries must make sense. Furthermore, their Maps must be compatible, that is, the MultiVectors' local dimensions must be the same on all processes.
This method must always be called as a collective operation on all processes over which the multivector is distributed. This is because the method reserves the right to check for compatibility of the two Maps, at least in debug mode, and throw if they are not compatible.
|
related |
Return a deep copy of the given MultiVector.
|
staticprotected |
Whether sumIntoLocalValue and sumIntoGlobalValue should use atomic updates by default.
Definition at line 806 of file Tpetra_MultiVector_decl.hpp.
|
mutableprotected |
The Kokkos::DualView containing the MultiVector's data.
This has to be declared mutable, so that get1dView() can retain its current const marking, even though it has always implied a device->host synchronization. Lesson to the reader: Use const sparingly!
Definition at line 2197 of file Tpetra_MultiVector_decl.hpp.
|
mutableprotected |
The "original view" of the MultiVector's data.
Methods like offsetView() return a view of a contiguous subset of rows. At some point, we might like to get all of the rows back, by taking another view of a superset of rows. For example, we might like to get a column Map view of a (domain Map view of a (column Map MultiVector)). Tpetra's implementation of Gauss-Seidel and SOR in CrsMatrix relies on this functionality. However, Kokkos (rightfully) forbids us from taking a superset of rows of the current view.
We deal with this at the Tpetra level by keeping around the original view of all the rows (and columns), which is origView_. Methods like offsetView() then use origView_, not view_, to make the subview for the returned MultiVector. Furthermore, offsetView() can do error checking by getting the original number of rows from origView_.
This may pose some problems for offsetView if it is given an offset other than zero, but that case is hardly exercised, so I am not going to worry about it for now.
Note that the "original" view isn't always original. It always has the original number of rows. However, some special cases of constructors that take a whichVectors argument, when whichVectors.size() is 1, may point origView_ to the column to view. Those constructors do this so that the resulting MultiVector has constant stride. This special case does not affect correctness of offsetView and related methods.
Definition at line 2228 of file Tpetra_MultiVector_decl.hpp.
|
protected |
Indices of columns this multivector is viewing.
If this array has nonzero size, then this multivector is a view of another multivector (the "original" multivector). In that case, whichVectors_ contains the indices of the columns of the original multivector. Furthermore, isConstantStride() returns false in this case.
If this array has zero size, then this multivector is not a view of any other multivector. Furthermore, the stride between columns of this multivector is a constant: thus, isConstantStride() returns true.
Definition at line 2242 of file Tpetra_MultiVector_decl.hpp.
|
protectedinherited |
The Map over which this object is distributed.
Definition at line 905 of file Tpetra_DistObject_decl.hpp.
|
protectedinherited |
Buffer into which packed data are imported (received from other processes).
Unfortunately, I had to declare these protected, because CrsMatrix uses them at one point. Please, nobody else use them.
Definition at line 918 of file Tpetra_DistObject_decl.hpp.
|
protectedinherited |
Number of packets to receive for each receive operation.
This array is used in Distributor::doPosts() (and doReversePosts()) when starting the ireceive operation.
This may be ignored in doTransfer() if constantNumPackets is nonzero, indicating a constant number of packets per LID. (For example, MultiVector sets the constantNumPackets output argument of packAndPrepare() to the number of columns in the multivector.)
Unfortunately, I had to declare this protected, because CrsMatrix uses it at one point. Please, nobody else use it.
Definition at line 956 of file Tpetra_DistObject_decl.hpp.
|
protectedinherited |
Buffer from which packed data are exported (sent to other processes).
Unfortunately, I had to declare this protected, because CrsMatrix uses it at one point. Please, nobody else use it.
Definition at line 963 of file Tpetra_DistObject_decl.hpp.
|
protectedinherited |
Number of packets to send for each send operation.
This array is used in Distributor::doPosts() (and doReversePosts()) for preparing for the send operation.
This may be ignored in doTransfer() if constantNumPackets is nonzero, indicating a constant number of packets per LID. (For example, MultiVector sets the constantNumPackets output argument of packAndPrepare() to the number of columns in the multivector.)
Unfortunately, I had to declare this protected, because CrsMatrix uses them at one point. Please, nobody else use it.
Definition at line 978 of file Tpetra_DistObject_decl.hpp.
 1.8.5
1.8.5