Pure abstract base interface for evaluating a stateless "model" that can be mapped into a number of different types of problems. More...

#include <Thyra_ModelEvaluator.hpp>

Inheritance diagram for Thyra::ModelEvaluator< Scalar >:

[legend]

Public Types
typedef Teuchos::ScalarTraits < Scalar >::magnitudeType	ScalarMag

Public Types inherited from Thyra::ModelEvaluatorBase
enum	EInArgsMembers { IN_ARG_x_dot_dot, IN_ARG_x_dot, IN_ARG_x, IN_ARG_x_dot_poly, IN_ARG_x_poly, IN_ARG_x_dot_mp, IN_ARG_x_mp, IN_ARG_t, IN_ARG_alpha, IN_ARG_beta, IN_ARG_W_x_dot_dot_coeff, IN_ARG_step_size, IN_ARG_stage_number }

enum	EInArgs_p_mp { IN_ARG_p_mp }

enum	EEvalType { , EVAL_TYPE_APPROX_DERIV, EVAL_TYPE_VERY_APPROX_DERIV }
	The type of an evaluation. More...

enum	EDerivativeMultiVectorOrientation { DERIV_MV_JACOBIAN_FORM, DERIV_MV_GRADIENT_FORM, DERIV_MV_BY_COL = DERIV_MV_JACOBIAN_FORM, DERIV_TRANS_MV_BY_ROW = DERIV_MV_GRADIENT_FORM }

enum	EDerivativeLinearOp { DERIV_LINEAR_OP }

enum	EDerivativeLinearity { DERIV_LINEARITY_UNKNOWN, DERIV_LINEARITY_CONST, DERIV_LINEARITY_NONCONST }

enum	ERankStatus { DERIV_RANK_UNKNOWN, DERIV_RANK_FULL, DERIV_RANK_DEFICIENT }

enum	EOutArgsMembers { OUT_ARG_f, OUT_ARG_W, OUT_ARG_f_mp, OUT_ARG_W_mp, OUT_ARG_W_op, OUT_ARG_W_prec, OUT_ARG_f_poly }

enum	EOutArgsDfDp { OUT_ARG_DfDp }

enum	EOutArgsDgDx_dot { OUT_ARG_DgDx_dot }

enum	EOutArgsDgDx { OUT_ARG_DgDx }

enum	EOutArgsDgDp { OUT_ARG_DgDp }

enum	EOutArgs_hess_vec_prod_f_xx { OUT_ARG_hess_vec_prod_f_xx }

enum	EOutArgs_hess_vec_prod_f_xp { OUT_ARG_hess_vec_prod_f_xp }

enum	EOutArgs_hess_vec_prod_f_px { OUT_ARG_hess_vec_prod_f_px }

enum	EOutArgs_hess_vec_prod_f_pp { OUT_ARG_hess_vec_prod_f_pp }

enum	EOutArgs_hess_vec_prod_g_xx { OUT_ARG_hess_vec_prod_g_xx }

enum	EOutArgs_hess_vec_prod_g_xp { OUT_ARG_hess_vec_prod_g_xp }

enum	EOutArgs_hess_vec_prod_g_px { OUT_ARG_hess_vec_prod_g_px }

enum	EOutArgs_hess_vec_prod_g_pp { OUT_ARG_hess_vec_prod_g_pp }

enum	EOutArgs_hess_f_xx { OUT_ARG_hess_f_xx }

enum	EOutArgs_hess_f_xp { OUT_ARG_hess_f_xp }

enum	EOutArgs_hess_f_pp { OUT_ARG_hess_f_pp }

enum	EOutArgs_hess_g_xx { OUT_ARG_hess_g_xx }

enum	EOutArgs_hess_g_xp { OUT_ARG_hess_g_xp }

enum	EOutArgs_hess_g_pp { OUT_ARG_hess_g_pp }

enum	EOutArgs_H_xx { OUT_ARG_H_xx }

enum	EOutArgs_H_xp { OUT_ARG_H_xp }

enum	EOutArgs_H_pp { OUT_ARG_H_pp }

enum	EOutArgsDfDp_mp { OUT_ARG_DfDp_mp }

enum	EOutArgs_g_mp { OUT_ARG_g_mp }

enum	EOutArgsDgDx_dot_mp { OUT_ARG_DgDx_dot_mp }

enum	EOutArgsDgDx_mp { OUT_ARG_DgDx_mp }

enum	EOutArgsDgDp_mp { OUT_ARG_DgDp_mp }

Basic information
virtual int	Np () const =0
	Return the number of sets of auxiliary parameters. More...

virtual int	Ng () const =0
	Return the number of sets of auxiliary response functions. More...

Vector spaces
virtual RCP< const VectorSpaceBase< Scalar > >	get_x_space () const =0
	Return the vector space for the state variables `x <: RE^n_x`. More...

virtual RCP< const VectorSpaceBase< Scalar > >	get_f_space () const =0
	Return the vector space for the state function `f(...) <: RE^n_x`. More...

virtual RCP< const VectorSpaceBase< Scalar > >	get_f_multiplier_space () const =0
	Return the dual vector space for the state function `f(...) <: RE^n_x`. More...

virtual RCP< const VectorSpaceBase< Scalar > >	get_p_space (int l) const =0
	Return the vector space for the auxiliary parameters `p(l) <: RE^n_p_l`. More...

virtual RCP< const Teuchos::Array< std::string > >	get_p_names (int l) const =0
	Get the names of the parameters associated with parameter subvector l if available. More...

virtual RCP< const VectorSpaceBase< Scalar > >	get_g_space (int j) const =0
	Return the vector space for the auxiliary response functions `g(j) <: RE^n_g_j`. More...

virtual RCP< const VectorSpaceBase< Scalar > >	get_g_multiplier_space (int j) const =0
	Return the dual vector space for the auxiliary response functions `g(j) <: RE^n_g_j`. More...

virtual Teuchos::ArrayView < const std::string >	get_g_names (int j) const =0
	Get the names of the response functions associated with subvector j if available. More...

Initial guess and upper and lower bounds
virtual ModelEvaluatorBase::InArgs < Scalar >	getNominalValues () const =0
	Return the set of nominal values or initial guesses for the supported the input arguments. More...

virtual ModelEvaluatorBase::InArgs < Scalar >	getLowerBounds () const =0
	Return the set of lower bounds for the input arguments. More...

virtual ModelEvaluatorBase::InArgs < Scalar >	getUpperBounds () const =0
	Return the set of upper bounds for the input arguments. More...

Factory functions for creating derivative objects
virtual RCP < LinearOpWithSolveBase < Scalar > >	create_W () const =0
	If supported, create a `LinearOpWithSolveBase` object for `W` to be evaluated. More...

virtual RCP< LinearOpBase < Scalar > >	create_W_op () const =0
	If supported, create a `LinearOpBase` object for `W` to be evaluated. More...

virtual RCP < PreconditionerBase< Scalar > >	create_W_prec () const =0
	If supported, create a `PreconditionerBase` object for `W_prec` to be evaluated. More...

virtual RCP< LinearOpBase < Scalar > >	create_DfDp_op (int l) const =0
	If supported, create a linear operator derivative object for `D(f)/D(p(l))`. More...

virtual RCP< LinearOpBase < Scalar > >	create_DgDx_dot_op (int j) const =0
	If supported, create a linear operator derivative object for `D(g(j))/D(x_dot)`. More...

virtual RCP< LinearOpBase < Scalar > >	create_DgDx_op (int j) const =0
	If supported, create a linear operator derivative object for `D(g(j))/D(x)`. More...

virtual RCP< LinearOpBase < Scalar > >	create_DgDp_op (int j, int l) const =0
	If supported, create a linear operator derivative object for `D(g(j))/D(p(l))`. More...

virtual RCP< LinearOpBase < Scalar > >	create_hess_f_xx () const =0
	If supported, create a linear operator derivative object for 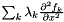$\sum_k \lambda_k \frac{\partial^2 f_k}{\partial \boldsymbol{x}^2}$ . More...

virtual RCP< LinearOpBase < Scalar > >	create_hess_f_xp (int l) const =0
	If supported, create a linear operator derivative object for 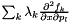$\sum_k \lambda_k \frac{\partial^2 f_k}{\partial \boldsymbol{x} \partial \boldsymbol{p}_l}$ . More...

virtual RCP< LinearOpBase < Scalar > >	create_hess_f_pp (int l1, int l2) const =0
	If supported, create a linear operator derivative object for 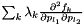$\sum_k \lambda_k \frac{\partial^2 f_k}{\partial \boldsymbol{p}_{l_1} \partial \boldsymbol{p}_{l_2}}$ . More...

virtual RCP< LinearOpBase < Scalar > >	create_hess_g_xx (int j) const =0
	If supported, create a linear operator derivative object for 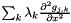$\sum_k \lambda_k \frac{\partial^2 g_{j,k}}{\partial \boldsymbol{x}^2}$ . More...

virtual RCP< LinearOpBase < Scalar > >	create_hess_g_xp (int j, int l) const =0
	If supported, create a linear operator derivative object for 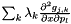$\sum_k \lambda_k \frac{\partial^2 g_{j,k}}{\partial \boldsymbol{x} \partial \boldsymbol{p}_{l}}$ . More...

virtual RCP< LinearOpBase < Scalar > >	create_hess_g_pp (int j, int l1, int l2) const =0
	If supported, create a linear operator derivative object for 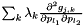$\sum_k \lambda_k \frac{\partial^2 g_{j,k}}{\partial \boldsymbol{p}_{l_1} \partial \boldsymbol{p}_{l_2}}$ . More...

Linear solver factory for W
virtual RCP< const LinearOpWithSolveFactoryBase < Scalar > >	get_W_factory () const =0
	If supported, return a `LinearOpWithSolveFactoryBase` object that can be used to initialize a `LOWSB` object for `W` given a `LOB` object for `W_op`. More...

Computational functions
virtual ModelEvaluatorBase::InArgs < Scalar >	createInArgs () const =0
	Create an empty input arguments object that can be set up and passed to `evalModel()`. More...

virtual ModelEvaluatorBase::OutArgs < Scalar >	createOutArgs () const =0
	Create an empty output functions/derivatives object that can be set up and passed to `evalModel()`. More...

virtual void	evalModel (const ModelEvaluatorBase::InArgs< Scalar > &inArgs, const ModelEvaluatorBase::OutArgs< Scalar > &outArgs) const =0
	Compute all of the requested functions/derivatives at the given point. More...

Reporting functions
virtual void	reportFinalPoint (const ModelEvaluatorBase::InArgs< Scalar > &finalPoint, const bool wasSolved)=0
	Report the final point and whether the problem was considered solved or not. More...

Additional Inherited Members
Public Member Functions inherited from Thyra::ModelEvaluatorBase
	ModelEvaluatorBase ()
	constructor More...

Static Public Attributes inherited from Thyra::ModelEvaluatorBase
static const int	NUM_E_IN_ARGS_MEMBERS =13

static const int	NUM_E_OUT_ARGS_MEMBERS =7

Related Functions inherited from Thyra::ModelEvaluatorBase
std::string	toString (ModelEvaluatorBase::EInArgsMembers)

std::string	toString (ModelEvaluatorBase::EOutArgsMembers)

std::string	toString (ModelEvaluatorBase::EDerivativeMultiVectorOrientation orientation)

ModelEvaluatorBase::EDerivativeMultiVectorOrientation	getOtherDerivativeMultiVectorOrientation (ModelEvaluatorBase::EDerivativeMultiVectorOrientation orientation)

Detailed Description

template<class Scalar>
class Thyra::ModelEvaluator< Scalar >

Pure abstract base interface for evaluating a stateless "model" that can be mapped into a number of different types of problems.

Outline

Introduction

This interface defines a very loosely mathematically typed interface to a very wide variety of simulation-based models that can support a very wide range of simulation-based numerical algorithms.

For the most part, a model represented by this interface is composed:

State vector function:

(x_dot_dot,x_dot,x,{p(l)},t,...}) -> f <: f_space
Auxiliary response vector functions:

(x_dot_dot,x_dot,x,{p(l)},t,...}) -> g(j) <: g_space(j), for j=0...Ng-1
Other outputs:

A model can compute other objects as well (see derivatives below).

given the general input variables/parameters:

State variables vector:

x <: x_space
State variables derivative w.r.t. t vector:

x_dot <: x_space
State variables second derivative w.r.t. t vector:

x_dot_dot <: x_space
Auxiliary parameter vectors:

p(l) <: p_space(l), for l=0...Np-1
Time point (or some other independent variable):

t <: Scalar
Other inputs:

A model can accept additional input objects as well (see below).

where x_space <: RE^n_x, f_space <: RE^n_x, p_space(l) <: RE^n_p_l (for l=0...Np-1), and g_space(j) <: RE^n_g_j (for j=0...Ng-1) are Thyra vector spaces of the given dimensions.

Above, the notation {p(l)} is shorthand for the set of parameter vectors { p(0), p(1), ..., p(Np-1) }.

All of the above variables/parameters and functions are represented as abstract Thyra::VectorBase objects. The vector spaces associated with these vector quantities are returned by get_x_space(), get_p_space(), get_f_space(), and get_g_space().

All of the input variables/parameters are specified as a ModelEvaluatorBase::InArgs object, all functions to be computed are specified as a ModelEvaluatorBase::OutArgs object, and evaluations of all function at a single set of variable values is performed in a single call to evalModel().

A particular ModelEvaluator subclass object can support any subset of these inputs and outputs and it is up to the client to map these variables/parameters and functions into abstract mathematical problems. Some of the different types of abstract mathematical problems that can be represented through this interface are given in the next section.

This interface can also support the computation of various derivatives of these functions w.r.t. the input arguments (see the section Function derivatives and sensitivities below).

Examples of Abstract Problem Types

There are a number of different types of mathematical problems that can be formulated using this interface. In the following subsections, a few different examples of specific abstract problems types are given.

Nonlinear Equations

   f(x) = 0

Here it is assumed that D(f)/D(x) is nonsingular in general but this is not strictly required. If W=D(f)/D(x) is supported, the nature of D(f)/D(x) may be given by this->createOutArgs().get_W_properties().

Explicit ODEs

   x_dot = f(x,t)

Here it is assumed that D(f)/D(x) is nonsingular in general but this is not strictly required. If W=D(f)/D(x) is supported, the nature of D(f)/D(x) may be given by this->createOutArgs().get_W_properties().

Above, the argument t may or may not be accepted by the model (i.e. createInArgs().supports(IN_ARG_t) may return false).

Implicit ODEs or DAEs

   f(x_dot,x,t) = 0

Here it is assumed that D(f)/D(x) is nonsingular in general but this is not strictly required.

The problem is either an implicit ODE or DAE depending on the nature of the derivative matrix D(f)/D(x_dot):

ODE: D(f)/D(x_dot) is full rank
DAE: D(f)/D(x_dot) is not full rank

If supported, the nature of W=W_x_dot_dot_coeff*D(f)/D(x_dot_dot)+alpha*D(f)/D(x_dot)+beta*D(f)/D(x) may be given by this->createOutArgs().get_W_properties().

Here the argument t may or may not be accepted by *this.

Unconstrained optimization

   min g(x,{p(l)})

where the objective function g(x,{p(l)}) is some aggregated function built from some subset of the the auxiliary response functions g(j)(x,{p(l)}), for j=1...Ng.

In general, it would be assumed that the Hessian D^2(g)/D(x^2) is symmetric semidefinite but this is not strictly required.

Equality constrained optimization

   min g(x,{p(l)})

   s.t. f(x,{p(l)}) = 0

where the objective function g(x,{p(l)}) is some aggregated function built from some subset of the the auxiliary response functions g(j)(x,{p(l)}), for j=0...Ng-1.

Here it is assumed that D(f)/D(x) is nonsingular in general but this is not strictly required. If W=D(f)/D(x) is supported, the nature of D(f)/D(x) may be given by this->createOutArgs().get_W_properties().

General constrained optimization

   min g(x,{p(l)})

   s.t. f(x,{p(l)}) = 0
        r(x,{p(l)}) = 0
        hL <= h(x,{p(l)}) <= hU
        xL <= x <= xU
        pL(l) <= p(l) <= pU(l)

where the objective function g(x,{p(l)}) and the auxiliary equality r(x,{p(l)}) and inequality h(x,{p(l)}) constraint functions are aggregated functions built from some subset of the the auxiliary response functions g(j)(x,{p(l)}), for j=0...Ng-1. The auxiliary response functions for a particular model can be interpreted in a wide variety of ways and can be mapped into a number of different optimization problems.

Here it is assumed that D(f)/D(x) is nonsingular in general but this is not strictly required. If W=D(f)/D(x) is supported, the nature of D(f)/D(x) may be given by this->createOutArgs().get_W_properties().

Function derivatives and sensitivities

A model can also optionally support the computation of various derivatives of the underlying model functions. The primary use for these derivatives is in the computation of various types of sensitivities. Specifically, direct and adjoint sensitivities will be considered.

To illustrate the issues involved, consider a single auxiliary parameter p and a single auxiliary response function g of the form (x,p) => g. Assuming that (x,p) ==> f defines the state equation f(x,p)=0 and that D(f)/D(x) is full rank, then f(x,p)=0 defines the implicit function p ==> x(p). Given this implicit function, the reduced auxiliary function is

   g_hat(p) = g(x(p),p)

The reduced derivative D(g_hat)/D(p) is given as:

   D(g_hat)/D(p) = D(g)/D(x) * D(x)/D(p) + D(g)/D(p)

where

   D(x)/D(p) = - [D(f)/D(x)]^{-1} * [D(f)/D(p)]

Restated, the reduced derivative D(g_hat)/D(p) is given as:

   D(g_hat)/D(p) = - [D(g)/D(x)] * [D(f)/D(x)]^{-1} * [D(f)/D(p)] + D(g)/D(p)

The reduced derivative D(g_hat)/D(p) can be computed using the direct or the adjoint approaches.

The direct sensitivity approach first solves for

   D(x)/D(p) = - [D(f)/D(x)]^{-1} * [D(f)/D(p)]

explicitly, then computes

   D(g_hat)/D(p) = D(g)/D(x) * D(x)/D(p) + D(g)/D(p).

In this case, D(f)/D(p) is needed as a multivector since it forms the RHS for a set of linear equations. However, only the action of D(g)/D(x) on the multivector D(x)/D(p) is needed and therefore D(g)/D(x) can be returned as only a linear operator (i.e. a LinearOpBase object). Note that in Thyra a multivector is a linear operator and therefore every derivative object returned as a multivector automatically implements the forward and adjoint linear operators for the derivative operator.

The final derivative D(g)/D(p) should be returned as a multivector that can be added to the multivector D(g)/D(x)*D(x)/D(p).

The adjoint sensitivity approach computes

   D(g_hat)/D(p)^T =  [D(f)/D(p)]^T * ( - [D(f)/D(x)]^{-T} * [D(g)/D(x)]^T ) + [D(g)/D(p)]^T

by first solving the adjoint system

   Lambda = - [D(f)/D(x)]^{-T} * [D(g)/D(x)]^T

for the multivector Lambda and then computes

   D(g_hat)/D(p)^T =  [D(f)/D(p)]^T * Lambda + [D(g)/D(p)]^T.

In this case, [D(g)/D(x)]^T is needed as an explicit multivector since it forms the RHS for the linear adjoint equations. Also, only the adjoint operator application[D(f)/D(p)]^T is needed. And in this case, the multivector form of the adjoint [D(g)/D(p)]^T is required.

As demonstrated above, general derivative objects (e.g. D(f)/D(p), D(g)/D(x), and D(g)/D(p)) may be needed as either only a linear operator (where it's forward or adjoint application is required) or as a multivector for its forward or adjoint forms. A derivative D(h)/D(z) for some function h(z) can be supported in any of the following forms:

D(h)/D(z) as a LinearOpBase object where the forward and/or adjoint operator applications are supported
D(h)/D(z) as a MultiVectorBase object where each column in the multivector i represents D(h)/D(z(i)), the derivatives for all of the functions h for the single variable z(i)
[D(h)/D(z)]^T as a MultiVectorBase object where each column in the multivector k represents [D(h(k))/D(z)]^T, the derivatives for the function h(k) for all of the variables z

A model can sign up to compute any, or all, or none of these forms of a derivative and this information is returned from this->createOutArgs().supports(OUT_ARG_blah,...) as a ModelEvaluatorBase::DerivativeSupport object, where blah is either DfDp, DgDx_dot, DgDx, or DgDp. The LinearOpBase form of a derivative is supported if this->createOutArgs().supports(OUT_ARG_blah,...).supports(DERIV_LINEAR_OP)==true. The forward MultiVectorBase form of the derivative is supported if this->createOutArgs().supports(OUT_ARG_blah,...).supports(DERIV_MV_BY_COL)==true while the adjoint form of the derivative is supported if this->createOutArgs().supports(OUT_ARG_blah,...).supports(DERIV_TRANS_MV_BY_ROW)==true.

In order to accommodate these different forms of a derivative, the simple class ModelEvaluatorBase::Derivative is defined that can store either a LinearOpBase or one of two MultiVectorBase forms (i.e. forward or adjoint) of the derivative. A ModelEvaluatorBase::Derivative object can only store one (or zero) forms of a derivative object at one time.

We now describe each of these derivative objects in more detail:

State function f(x_dot,x,{p(l)},t,...) derivatives
- State variable derivatives
```
      W = alpha*D(f)/D(x_dot) + beta*D(f)/D(x)
```
  This derivative operator is a special object that is derived from the LinearOpWithSolveBase interface and therefore supports linear solves. Objects of this type are created with the function create_W() and set on the InArgs object before they are computed in evalModel(). Note that if the model does not define or support an x_dot vector then the scalars alpha and beta need not be supported.
  
  The LinearOpWithSolveBase form of this derivative is supported if this->createOutArgs().supports(OUT_ARG_W)==true. The LinearOpBase-only form (i.e. no solve operation is given) of this derivative is supported if this->createOutArgs().supports(OUT_ARG_W_op)==true. The W_op form of W is to be preferred when no linear solve with W will ever be needed. A valid implementation may support none, both, or either of these forms LOWSB and/or LOB of W.
  
  Also note that an underlying model may only support a single copy of W or W_op at one time. This is required to accommodate some types of underlying applications that are less flexible in how they maintain their memory and how they deal with their objects. Therefore, to accommodate these types of less ideal application implementations, if a client tries to create and maintain more than one W and/or W_op object at one time, then create_W() and create_W_op() may return null (or may throw an undetermined exception). However, every "good" implementation of this interface should support the creation and maintenance of as many W and/or W_op objects at one time as will fit into memory.
- State variable Taylor coefficients
  
  x_poly = 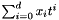$\sum_{i=0}^d x_i t^i$ ,
  
  x_dot_poly = 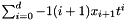$\sum_{i=0}^d-1 (i+1)x_{i+1} t^i$ ,
  
  f_poly = 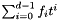$\sum_{i=0}^{d-1} f_i t^i$ .
  
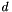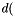
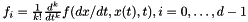  If x_poly is a given polynomial of degree and x_dot_poly = x_poly , then f_poly = f(x_poly, x_dot_poly, t) + $O(t^{d})$ where $f_i = \frac{1}{k!} \frac{d^k}{dt^k} f(dx/dt ,x(t),t), i=0,\ldots,d-1$ are the Taylor series coefficient of 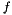. The polynomials x_poly, x_dot_poly, and f_poly are represented by Teuchos::Polynomial objects where each coefficient is a Thyra::VectorBase object. The Taylor series coefficients of 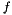can easily be computed using automatic differentiation, but this is generally the only means of doing so.
- Auxiliary parameter derivatives
```
      DfDp(l) = D(f)/D(p(l))
```
  for l=0...Np-1.
  
  These are derivative objects that represent the derivative of the state function f with respect to the auxiliary parameters p(l). This derivative is manipulated as a ModelEvaluatorBase::Derivative object.
Auxiliary response function g(j)(x,{p(l)},t,...) derivatives
- State variable derivatives
```
      DgDx_dot(j) = D(g(j))/D(x_dot)
```
  for j=0...Ng-1.
  
  These are derivative objects that represent the derivative of the auxiliary function g(j) with respect to the state variables derivative x_dot. This derivative is manipulated as a ModelEvaluatorBase::Derivative object.
```
      DgDx(j) = D(g(j))/D(x)
```
  for j=0...Ng-1.
  
  These are derivative objects that represent the derivative of the auxiliary function g(j) with respect to the state variables x. This derivative is manipulated as a ModelEvaluatorBase::Derivative object.
- Auxiliary parameter derivatives
```
      DgDp(j,l) = D(g(j))/D(p(l))
```
  for j=0...Ng-1, l=0...Np-1.
  
  These are derivative objects that represent the derivative of the auxiliary function g(j) with respect to the auxiliary parameters p(l). This derivative is manipulated as a ModelEvaluatorBase::Derivative object.
Second-order derivatives
- Second-order derivatives of the state function f(x_dot,x,{p(l)},t,...)
```
      hess_f_xx = sum(f_multiplier * D^2(f)/D(x)^2).
```
  This is a derivative object that represents the second-order derivative of the state function f with respect to the state variables x. This derivative is manipulated as a LinearOpBase object. Objects of this type are created with the function create_hess_f_xx().
```
      hess_f_xp(l) = sum(f_multiplier * D^2(f)/(D(x)D(p(l))))
```
  for l=0...Np-1.
  
  These are derivative objects that represent the second-order mixed partial derivative of the state function f with respect to both the state variables x and the auxiliary parameters p(l). This derivative is manipulated as a LinearOpBase object. Objects of this type are created with the function create_hess_f_xp(l).
```
      hess_f_pp(l1,l2) = sum(f_multiplier * D^2(f)/(D(p(l1))D(p(l2))))
```
  for l1=0...Np-1, l2=0...Np-1.
  
  These are derivative objects that represent the second-order mixed partial derivative of the state function f with respect to both the auxiliary parameters p(l1) and the auxiliary parameters p(l2). This derivative is manipulated as a LinearOpBase object. Objects of this type are created with the function create_hess_f_pp(l1,l2).
- Second-order derivatives of the auxiliary response function g(j)(x,{p(l)},t,...)
```
      hess_g_xx(j) = sum(g_multiplier(j) * D^2(g(j))/D(x)^2)
```
  for j=0...Ng-1.
  
  These are derivative objects that represent the second-order derivative of the auxiliary function g(j) with respect to the state variables x. This derivative is manipulated as a LinearOpBase object. Objects of this type are created with the function create_hess_g_xx(j).
```
      hess_g_xp(j,l) = sum(g_multiplier(j) * D^2(g(j))/(D(x)D(p(l))))
```
  for j=0...Ng-1, l=0...Np-1.
  
  These are derivative objects that represent the second-order mixed partial derivative of the auxiliary function g(j) with respect to both the state variables x and the auxiliary parameters p(l). This derivative is manipulated as a LinearOpBase object. Objects of this type are created with the function create_hess_g_xp(j,l).
```
      hess_g_pp(j,l1,l2) = sum(g_multiplier(j) * D^2(g(j))/(D(p(l1))D(p(l2))))
```
  for j=0...Ng-1, l1=0...Np-1, l2=0...Np-1.
  
  These are derivative objects that represent the second-order mixed partial derivative of the auxiliary function g(j) with respect to both the auxiliary parameters p(l1) and the auxiliary parameters p(l2). This derivative is manipulated as a LinearOpBase object. Objects of this type are created with the function create_hess_g_pp(j,l1,l2).

Nominal values

A model can optionally define a nominal value for any of the input arguments and these are returned from the getNominalValues() function as a const ModelEvaluatorBase::InArgs object. These nominal values can be used as initial guesses, as typical values (e.g. for scaling), or for other purposes. See evalModel() a discussion of how nonminal values are treated in an evaluation where the client does not pass in the values explicitly.

Variable and Function Bounds

A model can optionally define a set of upper and/or lower bounds for each of the input variables/parameters. These bounds are returned as const ModelEvaluatorBase::InArgs objects from the functions getLowerBounds() and getUpperBounds(). These bounds are typically used to define regions in space where the model functions are well defined. A client algorithm is free to ignore these bounds if they can not handle these types of constraints.

That fact that a model can defined reasonable bounds but most numerical algorithms can not handle bounds is no reason to leave bounds out of this interface. Again, if the client algorithm can not handle bounds then then can be simply ignored and there is not harm done (except the client algorithm might run into lots of trouble computing functions with undefined values)..

Significance of Parameter Subvectors

The parameters for any particular model are partitioned into different subvectors p(l) for several different reasons:

Parameters are grouped together into a subvectors p(l) to allow an ANA to manipulate an entire set at a time for different purposes. It is up to someone to select which parameters from a model will be exposed in a parameter subvector and how they are partitioned into subvectors. For example, one parameter subvector may be used a design parameters, while another subvector may be used for uncertain parameters, while still another may be used as continuation parameters.
Parameters are grouped together into subvectors p(l) implies that certain derivatives will be supplied for all the parameters in the subvector or none. If an ANA wants to flexibility to get the derivative for any individual scalar parameter by itself, then the paramters must be segregated into different parameter subvectors p(l) with one component each (e.g. get_p_space(l)->dim()==1).

Failed evaluations

The way for a ModelEvalutor object to return a failed evaluation is to set NaN in one or more of the output objects. If an algebraic model executes and happens to pass a negative number to a squareroot or something, then a NaN is what will get created anyway (even if the ModelEvaluator object does not detect this). Therefore, clients of the ME interface really need to be searching for a NaN to see if an evaluation has faield. Also, a ME object can set the isFailed flag on the outArgs object on the return from the evalModel() function if it knows that the evaluation has failed for some reason.

Inexact function evaluations

The ModelEvaluator interface supports inexact function evaluations for f and g(j). This is supported through the use of the type ModelEvaluatorBase::Evaluation which associates an enum ModelEvaluatorBase::EEvalType with each VectorBase object. By default, the evaluation type is ModelEvaluatorBase::EVAL_TYPE_EXACT. However, a client ANA can request or allow more inexact (and faster) evaluations for different purposes. For example, ModelEvaluatorBase::EVAL_TYPE_APPROX_DERIV would be used for finite difference approximations to the Jacobian-vector products and ModelEvaluatorBase::EVAL_TYPE_VERA_APPROX_DERIV would be used for finite difference Jacobian preconditioner approximations.

The type ModelEvaluatorBase::Evaluation is designed so that it can be seamlessly copied to and from a Teuchos::RCP object storing the VectorBase object. That means that if a client ANA requests an evaluation and just assumes an exact evaluation it can just set an RCP<VectorBase> object and ignore the presences of the evaluation type. Likewise, if a ModelEvaluator subclass does not support inexact evaluations, it can simply grab the vector object out of the OutArgs object as an RCP<VectorBase> object and ignore the evaluation type. However, any generic software (e.g. DECORATORS and COMPOSITES) must handle these objects as Evaluation objects and not RCP objects or the eval type info will be lost (see below).

If some bit of software converts from an Evaluation object to an RCP and then coverts back to an Evaluation object (perhaps by accident), this will slice off the evaluation type enum value and the resulting eval type will be the default EVAL_TYPE_EXACT. The worse thing that will likely happen in this case is that a more expensive evaluation will occur. Again, general software should avoid this.

Design Consideration: By putting the evaluation type into the OutArg output object itself instead of using a different data object, we avoid the risk of having some bit of software setting the evaluation type enum as inexact for one part of the computation (e.g. a finite difference Jacobian mat-vec) and then another bit of software reusing the OutArgs object and be computing inexact evaluation when they really wanted an exact evaluation (e.g. a line search algorithm). That could be a very difficult defect to track down in the ANA. For example, this could cause a line search method to fail due to an inexact evaluation. Therefore, the current design has the advantage of being biased toward exact evaluations and allowing clients and subclasses to ignore inexactness but has the disadvantage of allowing general code to slice off the evaluation type enum without even as much as a compile-time or any other type of warning.

Compile-Time and Run-Time Safety and Checking

The ModelEvaluator interface is designed to allow for great flexibility in how models are defined. The idea is that, at runtime, a model can decide what input and output arguments it will support and client algorithms must decide how to interpret what the model provides in order to form an abstract problem to solve. As a result, the ModelEvaluator interface is weakly typed mathematically. However, the interface is strongly typed in terms of the types of objects involved. For example, while a single ModelEvaluator object can represent anything and everything from a set of nonlinear equations to a full-blown constrained transient optimization problem, if the state vector x is supported, it must be manipulated as a VectorBase object, and this is checked at comple time.

In order for highly dynamically configurable software to be safe and usable, a great deal of runtime checking and good error reporting is required. Practically all of the runtime checking and error reporting work associated with a ModelEvaluator object is handled by the concrete ModelEvaluatorBase::InArgs and ModelEvaluatorBase::OutArgs classes. Once a concrete ModelEvaluator object has setup what input and output arguments the model supports, as returned by the createInArgs() and createOutArgs() functions, all runtime checking for the proper setting of input and output arguments and error reporting is automatically handled.

Notes to subclass developers

Nearly every subclass should directly or indirectly derive from the node subclass ModelEvaluatorDefaultBase since provides checking for correct specification of a model evaluator subclass and provides default implementations for various features.

Subclass developers should consider deriving from one (but not more than one) of the following subclasses rather than directly deriving from ModelEvaluatorDefaultBase:

StateFuncModelEvaluatorBase makes it easy to create models that start with the state function evaluation x -> f(x).
ResponseOnlyModelEvaluatorBase makes it easy to create models that start with the non-state response evaluation p -> g(p).
ModelEvaluatorDelegatorBase makes it easy to develop and maintain different types of decorator subclasses.

When deriving from any of the above intermediate base classes, the subclass can override any of virtual functions in any way that it would like. Therefore these subclasses just make the job of creating concrete subclasses easier without removing any of the flexibility of creating a subclass.

ToDo: Finish Documentation!

Definition at line 774 of file Thyra_ModelEvaluator.hpp.

Member Typedef Documentation

template<class Scalar>

typedef Teuchos::ScalarTraits<Scalar>::magnitudeType Thyra::ModelEvaluator< Scalar >::ScalarMag

Definition at line 778 of file Thyra_ModelEvaluator.hpp.

Member Function Documentation

template<class Scalar>

virtual int Thyra::ModelEvaluator< Scalar >::Np ( ) const

pure virtual

Return the number of sets of auxiliary parameters.

If this function returns 0, then there are no auxiliary parameters.

Implemented in Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::ModelEvaluatorDefaultBase< Scalar >, Thyra::ModelEvaluatorDefaultBase< double >, and Thyra::DiagonalQuadraticResponseOnlyModelEvaluator< Scalar >.

template<class Scalar>

virtual int Thyra::ModelEvaluator< Scalar >::Ng ( ) const

pure virtual

Return the number of sets of auxiliary response functions.

If this function returns 0, then there are no auxiliary response functions.

Implemented in Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::ModelEvaluatorDefaultBase< Scalar >, Thyra::ModelEvaluatorDefaultBase< double >, and Thyra::DiagonalQuadraticResponseOnlyModelEvaluator< Scalar >.

template<class Scalar>

virtual RCP<const VectorSpaceBase<Scalar> > Thyra::ModelEvaluator< Scalar >::get_x_space ( ) const

pure virtual

Return the vector space for the state variables x <: RE^n_x.

Implemented in Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, Thyra::Simple2DModelEvaluator< Scalar >, Thyra::DefaultStateEliminationModelEvaluator< Scalar >, and Thyra::ResponseOnlyModelEvaluatorBase< Scalar >.

template<class Scalar>

virtual RCP<const VectorSpaceBase<Scalar> > Thyra::ModelEvaluator< Scalar >::get_f_space ( ) const

pure virtual

Return the vector space for the state function f(...) <: RE^n_x.

Implemented in Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, Thyra::Simple2DModelEvaluator< Scalar >, Thyra::DefaultStateEliminationModelEvaluator< Scalar >, and Thyra::ResponseOnlyModelEvaluatorBase< Scalar >.

template<class Scalar>

virtual RCP<const VectorSpaceBase<Scalar> > Thyra::ModelEvaluator< Scalar >::get_f_multiplier_space ( ) const

pure virtual

Return the dual vector space for the state function f(...) <: RE^n_x.

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, Thyra::ModelEvaluatorDefaultBase< double >, and Thyra::ModelEvaluatorDelegatorBase< Scalar >.

template<class Scalar>

virtual RCP<const VectorSpaceBase<Scalar> > Thyra::ModelEvaluator< Scalar >::get_p_space ( int l ) const

pure virtual

Return the vector space for the auxiliary parameters p(l) <: RE^n_p_l.

Preconditions:

this->Np() > 0
0 <= l < this->Np()

Postconditions:

return.get()!=NULL

Implemented in Thyra::DefaultInverseModelEvaluator< Scalar >, Thyra::DefaultLumpedParameterModelEvaluator< Scalar >, Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::DiagonalQuadraticResponseOnlyModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, and Thyra::StateFuncModelEvaluatorBase< Scalar >.

template<class Scalar>

virtual RCP<const Teuchos::Array<std::string> > Thyra::ModelEvaluator< Scalar >::get_p_names ( int l ) const

pure virtual

Get the names of the parameters associated with parameter subvector l if available.

Returns: Returns an RCP to a Teuchos::Array<std::string> object that contains the names of the parameters. If returnVal == Teuchos::null, then there are no names available for the parameter subvector p(l). If returnVal->size() == 1, then a single name is given to the entire parameter subvector. If returnVal->size() == get_p_space(l)->dim(), then a name is given to every parameter scalar entry.

The default implementation return returnVal==Teuchos::null which means by default, parameters have no names associated with them.

Implemented in Thyra::DefaultLumpedParameterModelEvaluator< Scalar >, Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, Thyra::ResponseOnlyModelEvaluatorBase< Scalar >, and Thyra::StateFuncModelEvaluatorBase< Scalar >.

template<class Scalar>

virtual RCP<const VectorSpaceBase<Scalar> > Thyra::ModelEvaluator< Scalar >::get_g_space ( int j ) const

pure virtual

Return the vector space for the auxiliary response functions g(j) <: RE^n_g_j.

Preconditions:

this->Ng() > 0
0 <= j < this->Ng()

Postconditions:

return.get()!=NULL

Implemented in Thyra::DefaultInverseModelEvaluator< Scalar >, Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::DiagonalQuadraticResponseOnlyModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, and Thyra::StateFuncModelEvaluatorBase< Scalar >.

template<class Scalar>

virtual RCP<const VectorSpaceBase<Scalar> > Thyra::ModelEvaluator< Scalar >::get_g_multiplier_space ( int j ) const

pure virtual

Return the dual vector space for the auxiliary response functions g(j) <: RE^n_g_j.

Preconditions:

this->Ng() > 0
0 <= j < this->Ng()

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, Thyra::ModelEvaluatorDefaultBase< double >, and Thyra::ModelEvaluatorDelegatorBase< Scalar >.

template<class Scalar>

virtual Teuchos::ArrayView<const std::string> Thyra::ModelEvaluator< Scalar >::get_g_names ( int j ) const

pure virtual

Get the names of the response functions associated with subvector j if available.

Returns: Returns a Teuchos::Array<cosnt std::string> object that contains the names of the responses. If returnVal.size() == 0, then there are no names available for the response subvector g(j). If returnVal.size() == 1, then a single name is given to the entire response subvector. If returnVal.size() == get_g_space(l)->dim(), then a name is given to every parameter scalar entry.

The default implementation return returnVal.size() == 0 which means by default, responses have no names associated with them.

Implemented in Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, Thyra::ResponseOnlyModelEvaluatorBase< Scalar >, and Thyra::StateFuncModelEvaluatorBase< Scalar >.

template<class Scalar>

virtual ModelEvaluatorBase::InArgs<Scalar> Thyra::ModelEvaluator< Scalar >::getNominalValues ( ) const

pure virtual

Return the set of nominal values or initial guesses for the supported the input arguments.

In most cases, when a supported input argument is not specified in an InArgs object passed to evalModel(), the nominal value is assumed (see evalModel() for more details).

A model does not have to return nominal values for every supported input argument. Therefore, just because returnVal.supports(IN_ARG_blah)==true, the client should not assume that returnVal.get_blah()!=null.

Warning! Clients should not try to modify the state of the contained objects. Doing so might invalidate the state of *this model or of other clients. This is a hole in the const support and the use of InArgs. If a client wants to modify a value, then a clone of that value should be created and reset on the returned InArgs object. Do not modify the values in place!

Implemented in Thyra::DefaultLumpedParameterModelEvaluator< Scalar >, Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::DefaultNominalBoundsOverrideModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, Thyra::Simple2DModelEvaluator< Scalar >, Thyra::DefaultStateEliminationModelEvaluator< Scalar >, Thyra::ResponseOnlyModelEvaluatorBase< Scalar >, and Thyra::StateFuncModelEvaluatorBase< Scalar >.

template<class Scalar>

virtual ModelEvaluatorBase::InArgs<Scalar> Thyra::ModelEvaluator< Scalar >::getLowerBounds ( ) const

pure virtual

Return the set of lower bounds for the input arguments.

It is not required for the client to supply lower bounds for every input argument. If a lower bound object for an input argument is null, then the bounds of negative infinity should be assumed by the client.

Warning! Clients should not try to modify the state of the contained objects. Doing so might invalidate the state of *this model or of other clients. This is a hole in the const support and the use of InArgs. If a client wants to modify a value, then a clone of that value should be created and reset on the returned InArgs object. Do not modify the values in place!

Implemented in Thyra::DefaultLumpedParameterModelEvaluator< Scalar >, Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::DefaultNominalBoundsOverrideModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, Thyra::DefaultStateEliminationModelEvaluator< Scalar >, Thyra::ResponseOnlyModelEvaluatorBase< Scalar >, and Thyra::StateFuncModelEvaluatorBase< Scalar >.

template<class Scalar>

virtual ModelEvaluatorBase::InArgs<Scalar> Thyra::ModelEvaluator< Scalar >::getUpperBounds ( ) const

pure virtual

Return the set of upper bounds for the input arguments.

It is not required for the client to supply upper bounds for every input argument. If an upper bound object for an input argument is null, then the bounds of positive infinity should be assumed by the client.

Warning! Clients should not try to modify the state of the contained objects. Doing so might invalidate the state of *this model or of other clients. This is a hole in the const support and the use of InArgs. If a client wants to modify a value, then a clone of that value should be created and reset on the returned InArgs object. Do not modify the values in place!

Implemented in Thyra::DefaultLumpedParameterModelEvaluator< Scalar >, Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::DefaultNominalBoundsOverrideModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, Thyra::DefaultStateEliminationModelEvaluator< Scalar >, Thyra::ResponseOnlyModelEvaluatorBase< Scalar >, and Thyra::StateFuncModelEvaluatorBase< Scalar >.

template<class Scalar>

virtual RCP<LinearOpWithSolveBase<Scalar> > Thyra::ModelEvaluator< Scalar >::create_W ( ) const

pure virtual

If supported, create a LinearOpWithSolveBase object for W to be evaluated.

Preconditions:

this->createOutArgs().supports(OUT_ARG_W)==true

Postconditions:

!is_null(returnVal)

Note that a model is only required to support a single W object if the precondition below is satisfied and if the client asks for more than one W object, the response should be to return null from this function.

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, Thyra::ModelEvaluatorDefaultBase< double >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DefaultStateEliminationModelEvaluator< Scalar >, Thyra::DefaultModelEvaluatorWithSolveFactory< Scalar >, and Thyra::ResponseOnlyModelEvaluatorBase< Scalar >.

template<class Scalar>

virtual RCP<LinearOpBase<Scalar> > Thyra::ModelEvaluator< Scalar >::create_W_op ( ) const

pure virtual

If supported, create a LinearOpBase object for W to be evaluated.

Preconditions:

this->createOutArgs().supports(OUT_ARG_W_op)==true

Postconditions:

!is_null(returnVal)
isPartiallyInitialized(*returnVal) || isFullyInitialized(*returnVal)

Note that a model is only required to support a single W_op object if the precondition below is satisfied and if the client asks for more than one W_op object, the response should be to return null from this function.

Also note the above post-condition that requires that a created W_op object also needs to be at least partially initialized. This means that its range and domain spaces must be fully formed and accessible. This greatly simplifies the creation of composite structures and simplifies the implementation of certain types of implicit ModelEvaluator subclasses.

Implemented in Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, Thyra::Simple2DModelEvaluator< Scalar >, Thyra::DefaultStateEliminationModelEvaluator< Scalar >, Thyra::ResponseOnlyModelEvaluatorBase< Scalar >, and Thyra::StateFuncModelEvaluatorBase< Scalar >.

template<class Scalar>

virtual RCP<PreconditionerBase<Scalar> > Thyra::ModelEvaluator< Scalar >::create_W_prec ( ) const

pure virtual

If supported, create a PreconditionerBase object for W_prec to be evaluated.

Preconditions:

this->createOutArgs().supports(OUT_ARG_W_prec)==true

Postconditions:

!is_null(returnVal)
isPartiallyInitialized(*returnVal-.someOp()) || isFullyInitialized(*returnVal->someOp())

Note that a model is only required to support a single W_prec object if the precondition below is satisfied and if the client asks for more than one W_prec object, the response should be to return null from this function.

Also note the above post-condition requires that the embedded preconditioner linear operators (signified by *W_prec->someOp()) needs to be at least partially initialized. This means that its range and domain spaces must be fully formed and accessible. This greatly simplifies the creation of composite structures and simplifies the implementation of certain types of implicit ModelEvaluator subclasses.

Implemented in Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, Thyra::Simple2DModelEvaluator< Scalar >, Thyra::ResponseOnlyModelEvaluatorBase< Scalar >, and Thyra::StateFuncModelEvaluatorBase< Scalar >.

template<class Scalar>

virtual RCP<LinearOpBase<Scalar> > Thyra::ModelEvaluator< Scalar >::create_DfDp_op ( int l ) const

pure virtual

If supported, create a linear operator derivative object for D(f)/D(p(l)).

Preconditions:

this->Np() > 0
0 <= l < this->Np()
outArgs.supports_DfDp(l).supports(DERIV_LINEAR_OP)==true, where outArgs = this->createOutArgs()

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, and Thyra::ModelEvaluatorDefaultBase< double >.

template<class Scalar>

virtual RCP<LinearOpBase<Scalar> > Thyra::ModelEvaluator< Scalar >::create_DgDx_dot_op ( int j ) const

pure virtual

If supported, create a linear operator derivative object for D(g(j))/D(x_dot).

Preconditions:

this->Ng() > 0
0 <= j < this->Ng()
outArgs.supports_DgDx_dot(j).supports(DERIV_LINEAR_OP)==true, where outArgs = this->createOutArgs()

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, and Thyra::ModelEvaluatorDefaultBase< double >.

template<class Scalar>

virtual RCP<LinearOpBase<Scalar> > Thyra::ModelEvaluator< Scalar >::create_DgDx_op ( int j ) const

pure virtual

If supported, create a linear operator derivative object for D(g(j))/D(x).

Preconditions:

this->Ng() > 0
0 <= j < this->Ng()
outArgs.supports_DgDx(j).supports(DERIV_LINEAR_OP)==true, where outArgs = this->createOutArgs()

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, and Thyra::ModelEvaluatorDefaultBase< double >.

template<class Scalar>

virtual RCP<LinearOpBase<Scalar> > Thyra::ModelEvaluator< Scalar >::create_DgDp_op	(	int	j,
		int	l
	)		const

pure virtual

If supported, create a linear operator derivative object for D(g(j))/D(p(l)).

Preconditions:

this->Ng() > 0
this->Np() > 0
0 <= j < this->Ng()
0 <= l < this->Np()
outArgs.supports_DgDp(j,l).supports(DERIV_LINEAR_OP)==true, where outArgs = this->createOutArgs()

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, and Thyra::ModelEvaluatorDefaultBase< double >.

template<class Scalar>

virtual RCP<LinearOpBase<Scalar> > Thyra::ModelEvaluator< Scalar >::create_hess_f_xx ( ) const

pure virtual

If supported, create a linear operator derivative object for 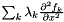$\sum_k \lambda_k \frac{\partial^2 f_k}{\partial \boldsymbol{x}^2}$ .

Preconditions:

this->createOutArgs().supports(OUT_ARG_hess_f_xx)==true

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, and Thyra::ModelEvaluatorDefaultBase< double >.

template<class Scalar>

virtual RCP<LinearOpBase<Scalar> > Thyra::ModelEvaluator< Scalar >::create_hess_f_xp ( int l ) const

pure virtual

If supported, create a linear operator derivative object for 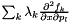$\sum_k \lambda_k \frac{\partial^2 f_k}{\partial \boldsymbol{x} \partial \boldsymbol{p}_l}$ .

Preconditions:

this->Np() > 0
0 <= l < this->Np()
this->createOutArgs().supports(l, OUT_ARG_hess_f_xp)==true

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, and Thyra::ModelEvaluatorDefaultBase< double >.

template<class Scalar>

virtual RCP<LinearOpBase<Scalar> > Thyra::ModelEvaluator< Scalar >::create_hess_f_pp	(	int	l1,
		int	l2
	)		const

pure virtual

If supported, create a linear operator derivative object for 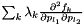$\sum_k \lambda_k \frac{\partial^2 f_k}{\partial \boldsymbol{p}_{l_1} \partial \boldsymbol{p}_{l_2}}$ .

Preconditions:

this->Ng() > 0
this->Np() > 0
0 <= j < this->Ng()
0 <= l_1 < this->Np()
0 <= l_2 < this->Np()
this->createOutArgs().supports(l_1, l_2, OUT_ARG_hess_f_pp)==true

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, and Thyra::ModelEvaluatorDefaultBase< double >.

template<class Scalar>

virtual RCP<LinearOpBase<Scalar> > Thyra::ModelEvaluator< Scalar >::create_hess_g_xx ( int j ) const

pure virtual

If supported, create a linear operator derivative object for 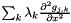$\sum_k \lambda_k \frac{\partial^2 g_{j,k}}{\partial \boldsymbol{x}^2}$ .

Preconditions:

this->Ng() > 0
0 <= j < this->Ng()
this->createOutArgs().supports(j, OUT_ARG_hess_g_xx)==true

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, and Thyra::ModelEvaluatorDefaultBase< double >.

template<class Scalar>

virtual RCP<LinearOpBase<Scalar> > Thyra::ModelEvaluator< Scalar >::create_hess_g_xp	(	int	j,
		int	l
	)		const

pure virtual

If supported, create a linear operator derivative object for 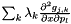$\sum_k \lambda_k \frac{\partial^2 g_{j,k}}{\partial \boldsymbol{x} \partial \boldsymbol{p}_{l}}$ .

Preconditions:

this->Ng() > 0
this->Np() > 0
0 <= j < this->Ng()
0 <= l < this->Np()
this->createOutArgs().supports(j, l, OUT_ARG_hess_g_xp)==true

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, and Thyra::ModelEvaluatorDefaultBase< double >.

template<class Scalar>

virtual RCP<LinearOpBase<Scalar> > Thyra::ModelEvaluator< Scalar >::create_hess_g_pp	(	int	j,
		int	l1,
		int	l2
	)		const

pure virtual

If supported, create a linear operator derivative object for 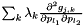$\sum_k \lambda_k \frac{\partial^2 g_{j,k}}{\partial \boldsymbol{p}_{l_1} \partial \boldsymbol{p}_{l_2}}$ .

Preconditions:

this->Ng() > 0
this->Np() > 0
0 <= j < this->Ng()
0 <= l_1 < this->Np()
0 <= l_2 < this->Np()
this->createOutArgs().supports(j, l_1, l_2, OUT_ARG_hess_g_xp)==true

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, and Thyra::ModelEvaluatorDefaultBase< double >.

template<class Scalar>

virtual RCP<const LinearOpWithSolveFactoryBase<Scalar> > Thyra::ModelEvaluator< Scalar >::get_W_factory ( ) const

pure virtual

If supported, return a LinearOpWithSolveFactoryBase object that can be used to initialize a LOWSB object for W given a LOB object for W_op.

Preconditions:

this->createOutArgs().supports(OUT_ARG_W) || this->createOutArgs().supports(OUT_ARG_W_op)

By returning this factory object, a model evaluator allows a client to compute the LOB-only version W_op and then allow client to create a linear solver associated through the LOWSB interface at any time. Note that this allow allows access to the underlying precondioner factory object (i.e. this->get_W_factory()->getPreconditionerFactory()</tt.) if such a factory object is supported.

This function will return retalVal==Teuchos::null if no such factory object is supported.

Implemented in Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, Thyra::Simple2DModelEvaluator< Scalar >, Thyra::DefaultModelEvaluatorWithSolveFactory< Scalar >, Thyra::ResponseOnlyModelEvaluatorBase< Scalar >, and Thyra::StateFuncModelEvaluatorBase< Scalar >.

template<class Scalar>

virtual ModelEvaluatorBase::InArgs<Scalar> Thyra::ModelEvaluator< Scalar >::createInArgs ( ) const

pure virtual

Create an empty input arguments object that can be set up and passed to evalModel().

Postconditions:

returnVal.supports(IN_ARG_blah) gives the variables that are supported or not supported by the underlying model.
returnVal.get_blah(...)==null for all variables/parameters that are supported.

Implemented in Thyra::DefaultInverseModelEvaluator< Scalar >, Thyra::EpetraModelEvaluator, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::DiagonalQuadraticResponseOnlyModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, Thyra::Simple2DModelEvaluator< Scalar >, and Thyra::DefaultStateEliminationModelEvaluator< Scalar >.

template<class Scalar>

virtual ModelEvaluatorBase::OutArgs<Scalar> Thyra::ModelEvaluator< Scalar >::createOutArgs ( ) const

pure virtual

Create an empty output functions/derivatives object that can be set up and passed to evalModel().

Postconditions:

returnVal.supports(OUT_ARG_blah...) gives the functions/derivatives that are supported or not supported by the underlying model.
returnVal.get_blah(...) == null for all functions/derivatives that are supported.

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, and Thyra::ModelEvaluatorDefaultBase< double >.

template<class Scalar>

virtual void Thyra::ModelEvaluator< Scalar >::evalModel	(	const ModelEvaluatorBase::InArgs< Scalar > &	inArgs,
		const ModelEvaluatorBase::OutArgs< Scalar > &	outArgs
	)		const

pure virtual

Compute all of the requested functions/derivatives at the given point.

Parameters

inArgs [in] Gives the values of the input variables and parameters that are supported by the model. This object must have been initially created by this->createInArgs() before being set up by the client. All supported variables/parameters that are not set by the client (i.e. inArgs.get_blah(...)==null) are assumed to be at the nominal value. If a particular input variable/parameter is not set and does not have a nominal value (i.e. this->getNominalValues().get_blah(...)==null, then the evaluation is undefined and an exception should be thrown by a good implementation. The two exceptions for this rule are support for x_dot and x_dot_dot. If x_dot or x_dot_dot are supported but not specified in inArgs, then it is implicitly assumed to be zero.

outArgs [out] Gives the objects for the supported functions and derivatives that are to be computed at the given point. This object must have been created by this->createOutArgs() before being set up by the client. Only functions and derivatives that are set will be computed. The client should check for NaN in any of objects computed to see if the evaluation failed. Also, if the underlying object knows that the evaluation failed, then outArgs.isFailed() will be true on output. The client needs to check for both NaN and outArgs.isFailed() to be sure.

Preconditions:

this->createInArgs().isCompatible(inArgs)==true
this->creatOutnArgs().isCompatible(outArgs)==true
[inArgs.supports(IN_ARG_blah)==true] inArgs.get_blah(...)!=null || this->getNominalValues().get_blah(...)!=null.
inArgs.get_p(l)!=null || this->getNominalValues().get_pl(l)!=null, for l=0...inArgs.Np()-1.

This function is the real meat of the ModelEvaluator interface. A whole set of supported functions and/or their various supported derivatives are computed all in one shot at a given point (i.e. set of values for input variables and parameters). This allows a model to be stateless in the sense that, in general, a model's behavior is assumed to be unaffected by evaluations at previous points. This greatly simplifies software maintenance and makes data dependences explicit.

WARNING: The implementation of this function must not create any persisting associations involving any of the input or output objects (even though these are returned through RCP objects). This includes not embedding any of the input objects in the created output objects. One reason for this requirement is that the RCP objects may not be strong owning RCPs in which case the objects may not stay around. This will likely result in a dangling reference exception in a debug-mode bulid (or a segfault in a non-debug build). Also, even if the objects do stay around, the implementation of evalModel(...) can not assume that the objects will not be further modified by the client after evalModel(...) is called. For example, the value of the vector returned from *inArgs.get_x() may changed by the client just after this function finishes which would invalidate any objects that might have expected it to not change.

TODO: Define behavior for state-full models!

Implemented in Thyra::ModelEvaluatorDefaultBase< Scalar >, and Thyra::ModelEvaluatorDefaultBase< double >.

template<class Scalar>

virtual void Thyra::ModelEvaluator< Scalar >::reportFinalPoint	(	const ModelEvaluatorBase::InArgs< Scalar > &	finalPoint,
		const bool	wasSolved
	)

pure virtual

Report the final point and whether the problem was considered solved or not.

ToDo: Add a PL to InArgs to allow extra data like Lagrange multipliers to be passed back as well?

Implemented in Thyra::EpetraModelEvaluator, Thyra::DefaultLumpedParameterModelEvaluator< Scalar >, Thyra::DefaultMultiPeriodModelEvaluator< Scalar >, Thyra::ModelEvaluatorDelegatorBase< Scalar >, Thyra::DummyTestModelEvaluator< Scalar >, Thyra::DefaultFinalPointCaptureModelEvaluator< Scalar >, Thyra::ResponseOnlyModelEvaluatorBase< Scalar >, and Thyra::StateFuncModelEvaluatorBase< Scalar >.

The documentation for this class was generated from the following file:

Thyra_ModelEvaluator.hpp

Public Types

Basic information

Vector spaces

Initial guess and upper and lower bounds

Factory functions for creating derivative objects

Linear solver factory for W

Computational functions

Reporting functions

Additional Inherited Members

Detailed Description

template<class Scalar> class Thyra::ModelEvaluator< Scalar >

Outline

Introduction

Examples of Abstract Problem Types

Nonlinear Equations

Explicit ODEs

Implicit ODEs or DAEs

Unconstrained optimization

Equality constrained optimization

General constrained optimization

Function derivatives and sensitivities

Nominal values

Variable and Function Bounds

Significance of Parameter Subvectors

Failed evaluations

Inexact function evaluations

Compile-Time and Run-Time Safety and Checking

Notes to subclass developers

Member Typedef Documentation

Member Function Documentation

template<class Scalar>
class Thyra::ModelEvaluator< Scalar >