|
Stokhos Package Browser (Single Doxygen Collection)
Version of the Day
|
|
Stokhos Package Browser (Single Doxygen Collection)
Version of the Day
|
Abstract base class for 1-D orthogonal polynomials. More...
#include <Stokhos_OneDOrthogPolyBasis.hpp>

Public Types | |
| typedef int(* | LevelToOrderFnPtr )(int level, int growth) |
| Function pointer needed for level_to_order mappings. More... | |
Public Member Functions | |
| OneDOrthogPolyBasis () | |
| Default constructor. More... | |
| virtual | ~OneDOrthogPolyBasis () |
| Destructor. More... | |
| virtual ordinal_type | order () const =0 |
Return order of basis (largest monomial degree 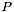 ). More... ). More... | |
| virtual ordinal_type | size () const =0 |
| Return total size of basis (given by order() + 1). More... | |
| virtual const Teuchos::Array < value_type > & | norm_squared () const =0 |
| Return array storing norm-squared of each basis polynomial. More... | |
| virtual const value_type & | norm_squared (ordinal_type i) const =0 |
Return norm squared of basis polynomial i. More... | |
| virtual Teuchos::RCP < Stokhos::Dense3Tensor < ordinal_type, value_type > > | computeTripleProductTensor () const =0 |
| Compute triple product tensor. More... | |
| virtual Teuchos::RCP < Stokhos::Sparse3Tensor < ordinal_type, value_type > > | computeSparseTripleProductTensor (ordinal_type order) const =0 |
| Compute triple product tensor. More... | |
| virtual Teuchos::RCP < Teuchos::SerialDenseMatrix < ordinal_type, value_type > > | computeDerivDoubleProductTensor () const =0 |
| Compute derivative double product tensor. More... | |
| virtual void | evaluateBases (const value_type &point, Teuchos::Array< value_type > &basis_pts) const =0 |
Evaluate each basis polynomial at given point point. More... | |
| virtual value_type | evaluate (const value_type &point, ordinal_type order) const =0 |
Evaluate basis polynomial given by order order at given point point. More... | |
| virtual void | print (std::ostream &os) const |
Print basis to stream os. More... | |
| virtual const std::string & | getName () const =0 |
| Return string name of basis. More... | |
| virtual void | getQuadPoints (ordinal_type quad_order, Teuchos::Array< value_type > &points, Teuchos::Array< value_type > &weights, Teuchos::Array< Teuchos::Array< value_type > > &values) const =0 |
Compute quadrature points, weights, and values of basis polynomials at given set of points points. More... | |
| virtual ordinal_type | quadDegreeOfExactness (ordinal_type n) const =0 |
| virtual Teuchos::RCP < OneDOrthogPolyBasis < ordinal_type, value_type > > | cloneWithOrder (ordinal_type p) const =0 |
| Clone this object with the option of building a higher order basis. More... | |
| virtual ordinal_type | coefficientGrowth (ordinal_type n) const =0 |
| Evaluate coefficient growth rule for Smolyak-type bases. More... | |
| virtual ordinal_type | pointGrowth (ordinal_type n) const =0 |
| Evaluate point growth rule for Smolyak-type bases. More... | |
| virtual LevelToOrderFnPtr | getSparseGridGrowthRule () const =0 |
| Get sparse grid level_to_order mapping function. More... | |
| virtual void | setSparseGridGrowthRule (LevelToOrderFnPtr ptr)=0 |
| Set sparse grid rule. More... | |
Private Member Functions | |
| OneDOrthogPolyBasis (const OneDOrthogPolyBasis &) | |
| OneDOrthogPolyBasis & | operator= (const OneDOrthogPolyBasis &b) |
Abstract base class for 1-D orthogonal polynomials.
This class provides an abstract interface for univariate orthogonal polynomials. Orthogonality is defined by the inner product
![\[ (f,g) = \langle fg \rangle = \int_{-\infty}^{\infty} f(x)g(x) \rho(x) dx \]](form_122.png)
where 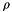 is the density function of the measure associated with the orthogonal polynomials. See Stokhos::RecurrenceBasis for a general implementation of this interface based on the three-term recurrence satisfied by these polynomials. Multivariate polynomials can be formed from a collection of univariate polynomials through tensor products (see Stokhos::CompletePolynomialBasis).
is the density function of the measure associated with the orthogonal polynomials. See Stokhos::RecurrenceBasis for a general implementation of this interface based on the three-term recurrence satisfied by these polynomials. Multivariate polynomials can be formed from a collection of univariate polynomials through tensor products (see Stokhos::CompletePolynomialBasis).
Like most classes in Stokhos, the class is templated on the ordinal and value types. Typically ordinal_type = int and value_type = double.
Definition at line 81 of file Stokhos_OneDOrthogPolyBasis.hpp.
| typedef int( * Stokhos::OneDOrthogPolyBasis< ordinal_type, value_type >::LevelToOrderFnPtr)(int level, int growth) |
Function pointer needed for level_to_order mappings.
Definition at line 204 of file Stokhos_OneDOrthogPolyBasis.hpp.
|
inline |
Default constructor.
Definition at line 85 of file Stokhos_OneDOrthogPolyBasis.hpp.
|
inlinevirtual |
Destructor.
Definition at line 88 of file Stokhos_OneDOrthogPolyBasis.hpp.
|
private |
|
pure virtual |
Return order of basis (largest monomial degree 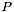 ).
).
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, and Stokhos::RecurrenceBasis< OrdinalType, ValueType >.
|
pure virtual |
Return total size of basis (given by order() + 1).
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, and Stokhos::RecurrenceBasis< OrdinalType, ValueType >.
|
pure virtual |
Return array storing norm-squared of each basis polynomial.
Entry 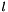 of returned array is given by
of returned array is given by 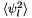 for
for 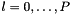 where
where 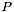 is given by order().
is given by order().
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, and Stokhos::RecurrenceBasis< OrdinalType, ValueType >.
|
pure virtual |
Return norm squared of basis polynomial i.
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, and Stokhos::RecurrenceBasis< OrdinalType, ValueType >.
|
pure virtual |
Compute triple product tensor.
The 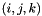 entry of the tensor
entry of the tensor 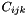 is given by
is given by 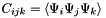 where
where 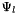 represents basis polynomial
represents basis polynomial 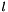 and
and 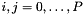 where
where 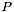 is size()-1 and
is size()-1 and 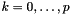 where
where 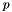 is the supplied
is the supplied order.
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, and Stokhos::RecurrenceBasis< OrdinalType, ValueType >.
|
pure virtual |
Compute triple product tensor.
The 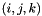 entry of the tensor
entry of the tensor 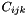 is given by
is given by 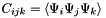 where
where 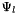 represents basis polynomial
represents basis polynomial 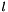 and
and 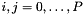 where
where 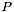 is size()-1 and
is size()-1 and 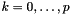 where
where 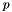 is the supplied
is the supplied order.
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, and Stokhos::RecurrenceBasis< OrdinalType, ValueType >.
|
pure virtual |
Compute derivative double product tensor.
The 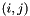 entry of the tensor
entry of the tensor 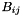 is given by
is given by 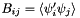 where
where 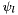 represents basis polynomial
represents basis polynomial 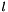 and
and 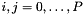 where
where 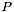 is the order of the basis.
is the order of the basis.
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, and Stokhos::RecurrenceBasis< OrdinalType, ValueType >.
|
pure virtual |
Evaluate each basis polynomial at given point point.
Size of returned array is given by size(), and coefficients are ordered from order 0 up to order order().
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, and Stokhos::RecurrenceBasis< OrdinalType, ValueType >.
|
pure virtual |
Evaluate basis polynomial given by order order at given point point.
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, and Stokhos::RecurrenceBasis< OrdinalType, ValueType >.
|
inlinevirtual |
Print basis to stream os.
Reimplemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, and Stokhos::RecurrenceBasis< OrdinalType, ValueType >.
Definition at line 157 of file Stokhos_OneDOrthogPolyBasis.hpp.
|
pure virtual |
Return string name of basis.
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, and Stokhos::RecurrenceBasis< OrdinalType, ValueType >.
|
pure virtual |
Compute quadrature points, weights, and values of basis polynomials at given set of points points.
quad_order specifies the order to which the quadrature should be accurate, not the number of quadrature points. The number of points is given by (quad_order + 1) / 2. Note however the passed arrays do NOT need to be sized correctly on input as they will be resized appropriately.
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, Stokhos::RecurrenceBasis< OrdinalType, ValueType >, Stokhos::LanczosPCEBasis< ordinal_type, value_type >, Stokhos::LanczosProjPCEBasis< ordinal_type, value_type >, Stokhos::LanczosPCEBasis< OrdinalType, ValueType >, Stokhos::LanczosProjPCEBasis< OrdinalType, ValueType >, Stokhos::StieltjesPCEBasis< ordinal_type, value_type >, Stokhos::StieltjesPCEBasis< OrdinalType, ValueType >, Stokhos::HouseTriDiagPCEBasis< ordinal_type, value_type >, Stokhos::MonoProjPCEBasis< ordinal_type, value_type >, Stokhos::StieltjesBasis< ordinal_type, value_type, func_type >, Stokhos::HouseTriDiagPCEBasis< OrdinalType, ValueType >, Stokhos::MonoProjPCEBasis< OrdinalType, ValueType >, Stokhos::ClenshawCurtisLegendreBasis< ordinal_type, value_type >, and Stokhos::GaussPattersonLegendreBasis< ordinal_type, value_type >.
|
pure virtual |
Return polynomial degree of exactness for a given number of quadrature points.
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, Stokhos::RecurrenceBasis< OrdinalType, ValueType >, Stokhos::ClenshawCurtisLegendreBasis< ordinal_type, value_type >, and Stokhos::GaussPattersonLegendreBasis< ordinal_type, value_type >.
|
pure virtual |
Clone this object with the option of building a higher order basis.
This method is following the Prototype pattern (see Design Pattern's textbook). The slight variation is that it allows the order of the polynomial to be modified, otherwise an exact copy is formed. The use case for this is creating basis functions for column indices in a spatially varying adaptive refinement context.
Implemented in Stokhos::JacobiBasis< ordinal_type, value_type >, Stokhos::LanczosPCEBasis< ordinal_type, value_type >, Stokhos::LanczosProjPCEBasis< ordinal_type, value_type >, Stokhos::LanczosPCEBasis< OrdinalType, ValueType >, Stokhos::LanczosProjPCEBasis< OrdinalType, ValueType >, Stokhos::StieltjesPCEBasis< ordinal_type, value_type >, Stokhos::StieltjesPCEBasis< OrdinalType, ValueType >, Stokhos::ClenshawCurtisLegendreBasis< ordinal_type, value_type >, Stokhos::GaussPattersonLegendreBasis< ordinal_type, value_type >, Stokhos::HouseTriDiagPCEBasis< ordinal_type, value_type >, Stokhos::MonoProjPCEBasis< ordinal_type, value_type >, Stokhos::StieltjesBasis< ordinal_type, value_type, func_type >, Stokhos::HouseTriDiagPCEBasis< OrdinalType, ValueType >, Stokhos::MonoProjPCEBasis< OrdinalType, ValueType >, Stokhos::DiscretizedStieltjesBasis< ordinal_type, value_type >, Stokhos::RysBasis< ordinal_type, value_type >, Stokhos::HermiteBasis< ordinal_type, value_type >, Stokhos::LegendreBasis< ordinal_type, value_type >, Stokhos::HermiteBasis< OrdinalType, ValueType >, and Stokhos::LegendreBasis< OrdinalType, ValueType >.
|
pure virtual |
Evaluate coefficient growth rule for Smolyak-type bases.
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, Stokhos::RecurrenceBasis< OrdinalType, ValueType >, Stokhos::ClenshawCurtisLegendreBasis< ordinal_type, value_type >, and Stokhos::GaussPattersonLegendreBasis< ordinal_type, value_type >.
|
pure virtual |
Evaluate point growth rule for Smolyak-type bases.
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, Stokhos::RecurrenceBasis< OrdinalType, ValueType >, Stokhos::ClenshawCurtisLegendreBasis< ordinal_type, value_type >, and Stokhos::GaussPattersonLegendreBasis< ordinal_type, value_type >.
|
pure virtual |
Get sparse grid level_to_order mapping function.
Predefined functions are: webbur::level_to_order_linear_wn Symmetric Gaussian linear growth webbur::level_to_order_linear_nn Asymmetric Gaussian linear growth webbur::level_to_order_exp_cc Clenshaw-Curtis exponential growth webbur::level_to_order_exp_gp Gauss-Patterson exponential growth webbur::level_to_order_exp_hgk Genz-Keister exponential growth webbur::level_to_order_exp_f2 Fejer-2 exponential growth
Implemented in Stokhos::RecurrenceBasis< ordinal_type, value_type >, and Stokhos::RecurrenceBasis< OrdinalType, ValueType >.
|
pure virtual |
Set sparse grid rule.
|
private |
 1.8.5
1.8.5