|
Stokhos Package Browser (Single Doxygen Collection)
Version of the Day
|
All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Groups Pages
|
Stokhos Package Browser (Single Doxygen Collection)
Version of the Day
|
Transforms a non-orthogonal multivariate basis to an orthogonal one using the Gram-Schmit procedure. More...
#include <Stokhos_GramSchmidtBasis.hpp>

Additional Inherited Members | |
 Public Member Functions inherited from Stokhos::OrthogPolyBasis< ordinal_type, value_type > Public Member Functions inherited from Stokhos::OrthogPolyBasis< ordinal_type, value_type > | |
| OrthogPolyBasis () | |
| Constructor. More... | |
| virtual | ~OrthogPolyBasis () |
| Destructor. More... | |
| virtual ordinal_type | order () const =0 |
| Return order of basis. More... | |
| virtual ordinal_type | dimension () const =0 |
| Return dimension of basis. More... | |
| virtual ordinal_type | size () const =0 |
| Return total size of basis. More... | |
| virtual const Teuchos::Array < value_type > & | norm_squared () const =0 |
| Return array storing norm-squared of each basis polynomial. More... | |
| virtual const value_type & | norm_squared (ordinal_type i) const =0 |
Return norm squared of basis polynomial i. More... | |
| virtual Teuchos::RCP < Stokhos::Sparse3Tensor < ordinal_type, value_type > > | computeTripleProductTensor () const =0 |
| Compute triple product tensor. More... | |
| virtual Teuchos::RCP < Stokhos::Sparse3Tensor < ordinal_type, value_type > > | computeLinearTripleProductTensor () const =0 |
| Compute linear triple product tensor where k = 0,1. More... | |
| virtual value_type | evaluateZero (ordinal_type i) const =0 |
Evaluate basis polynomial i at zero. More... | |
| virtual void | evaluateBases (const Teuchos::ArrayView< const value_type > &point, Teuchos::Array< value_type > &basis_vals) const =0 |
Evaluate basis polynomials at given point point. More... | |
| virtual void | print (std::ostream &os) const =0 |
Print basis to stream os. More... | |
| virtual const std::string & | getName () const =0 |
| Return string name of basis. More... | |
Transforms a non-orthogonal multivariate basis to an orthogonal one using the Gram-Schmit procedure.
Given a basis 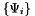 with an inner product defined by
with an inner product defined by
![\[ (\Psi_i,\Psi_j) = \sum_{k=0}^Q w_k\Psi_i(x_k)\Psi_j(x_k) \]](form_54.png)
where 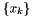 and
and 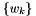 are a set of
are a set of 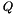 quadrature points and weights, this class generates a new basis
quadrature points and weights, this class generates a new basis 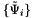 that satisfies
that satisfies 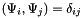 .
.
NOTE: Currently on the classical Gram-Schmidt algorithm is implemented.
Definition at line 72 of file Stokhos_GramSchmidtBasis.hpp.
 1.8.5
1.8.5