|
Komplex
Development
|
|
Komplex
Development
|
KOMPLEX is collection of software that solves complex-valued linear systems using an equivalent real-valued formulation. There are two versions of capabilities in this package:
KOMPLEX solves a complex-valued linear system 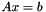 by solving an equivalent real-valued system of twice the dimension. Specifically, writing in terms of real and imaginary parts, we have
by solving an equivalent real-valued system of twice the dimension. Specifically, writing in terms of real and imaginary parts, we have
![\[ (A_r + i*A_i)*(x_r + i*x_i) = (b_r + i*b_i) \]](form_0.png)
or by separating into real and imaginary equations we have
![\[ \left( \begin{array}{rr} A_r & -A_i\\ A_i & A_r \end{array} \right) \left( \begin{array}{r} x_r\\ x_i \end{array} \right) = \left( \begin{array}{r} b_r\\ b_i \end{array} \right) \]](form_1.png)
which is a real-valued system of twice the size. If we find 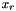 and
and 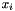 , we can form the solution to the original system as
, we can form the solution to the original system as 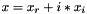 .
.
Note: Since Komplex builds with the standard Trilinos build process, the build process described below is not required when using Komplex with Trilinos.
Installation and use of Komplex assumes a good working knowledge of Aztec 2.1. To install Komplex 1.0, you must:
Follow the Aztec 2.1 installation procedure to install Aztec.
Compile.
Edit the files 'komplex_lib/Makefile.template' and 'komplex_app/Makefile.template'. Set the Makefile variables MPI_INCLUDE_DIR and MPI_LIB to the appropriate directories and libraries (if using MPI). For example
MPI_INCLUDE_DIR = -I/Net/local/mpi/include MPI_LIB = -L/Net/local/mpi -lmpich
TYPE ===> set_komplex_makefiles xxxx yyyy
where xxxx specifies a machine (SOLARIS, SUN4, SGI, SGIM4, SGI10K, I860, DEC, HP, SUNMOS, NCUBE, SP2, T3E, LINUX, or TFLOP) and yyyy specifies a messaging system (MPI, SERIAL, I860, SUNMOS, or NCUBE).
Example: set_komplex_makefiles SUN4 MPI
This creates 'Makefile.xxxx.yyyy' which is linked to Makefile.
TYPE ===> cd komplex_lib; make; cd ../komplex_app; make
'gmake' works on all machines except the Cray T3E where it appears necessary to uncomment Makefile lines refering to implicit compilation.
Other applications can be compiled by switching OBJ lines in app/Makefile.
NOTE: On some machines it is necessary to switch the linker 'LD_*' when the main program is Fortran.
When porting to other machines, the following issues are the most difficult:
Linking between Fortran and C differs between machines. 'lib/az_aztec.h' contains macros corresponding to CFORT in the Makefiles.
Note: See the class documentation for Komplex_LinearProblem for details on its use.
KOMPLEX accept user linear systems in three forms:
The first form is true complex. The user passes in an MSR or VBR format matrix where the values are stored like Fortran complex numbers. Thus, the values array is of type double that is twice as long as the number of complex values. Each complex entry is stored with real part followed by imaginary part (as in Fortran). See AZK_create_linsys_c2k.
The second form stores real and imaginary parts separately, but the pattern for each is identical. Thus only the values of the imaginary part are passed to the creation routines. See AZK_create_linsys_ri2k.
Each of the above forms supports a global or local index set. By this we mean that the index values (stored in bindx) refer to the global problem indices, or the local indices (for example after calling AZ_transform). Note that for Form 1 above, indices can be local or global but you cannot use AZ_transform if to create local indices since AZ_transform does not support complex matrices.
All input matrices are formed as AZ_MATRIX structs (see the Aztec 2.1 User Manual). Before using Komplex, you should become very familiar with Aztec.
Komplex has a very flexible create/destroy framework. Although the steps in Section Step-by-step use of Komplex refer to creating an entire linear system at one time, it is possible to create and destroy the matrix, initial guess and right hand side in separate steps. The matrix is created (destroyed) by calling AZK_matrix_create_xxx (AZK_matrix_destroy_xxx) where xxx refers to the type of input problem as described in Section Possible Formulations. Similarly, the initial guess and RHS can also be built separately. All Komplex objects are created from completely separate storage than what the user provides. As such they remain viable until destroyed.
A few scenarios:
The following example code generates a simple diagonal matrix of dimension "n" where "n" is passed in as an argument. The diagonal entries are constructed in a way that exactly 20 unpreconditioned GMRES iteration should be required for convergence, independent of problem size and number of processors used.
The point of this example is to illustrate the flow of calls when using KOMPLEX. This example program can be found in the file komplex_app/simple.c.
A more elaborate sample test program can be found in the file komplex_app/main.c. Note that it relies on service routines from SPARSKIT2. SPARSKIT2 is available at http://www.cs.umn.edu/Research/arpa/SPARSKIT/sparskit.html
/*******************************************************************************
* Copyright 2000, Sandia Corporation. The United States Government retains a *
* nonexclusive license in this software as prescribed in AL 88-1 and AL 91-7. *
* Export of this program may require a license from the United States *
* Government. *
******************************************************************************/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <mpi.h>
#include "az_aztec.h"
#include "azk_komplex.h"
int main(int argc, char *argv[])
{
int proc_config[AZ_PROC_SIZE];/* Processor information. */
int options[AZ_OPTIONS_SIZE]; /* Array used to select solver options. */
double params[AZ_PARAMS_SIZE]; /* User selected solver paramters. */
double status[AZ_STATUS_SIZE]; /* Information returned from AZ_solve(). */
int *bindx_real; /* index and values arrays for MSR matrices */
double *val_real, *val_imag;
int * update; /* List of global eqs owned by the processor */
double *x_real, *b_real; /* initial guess/solution, RHS */
double *x_imag, *b_imag;
int N_local; /* Number of equations on this node */
double residual; /* Used for computing residual */
double *xx_real, *xx_imag, *xx; /* Known exact solution */
int myPID, nprocs;
AZ_MATRIX *Amat_real; /* Real matrix structure */
AZ_MATRIX *Amat; /* Komplex matrix to be solved. */
AZ_PRECOND *Prec; /* Komplex preconditioner */
double *x, *b; /* Komplex Initial guess and RHS */
int i;
/******************************/
/* First executable statement */
/******************************/
MPI_Init(&argc,&argv);
/* Get number of processors and the name of this processor */
AZ_set_proc_config(proc_config,MPI_COMM_WORLD);
nprocs = proc_config[AZ_N_procs];
myPID = proc_config[AZ_node];
printf("proc %d of %d is alive\n",myPID, nprocs);
/* Define two real diagonal matrices. Will use as real and imaginary parts */
/* Get the number of local equations from the command line */
N_local = atoi(argv[1]);
/* Need N_local+1 elements for val/bindx arrays */
val_real = malloc((N_local+1)*sizeof(double));
val_imag = malloc((N_local+1)*sizeof(double));
/* bindx_imag is not needed since real/imag have same pattern */
bindx_real = malloc((N_local+1)*sizeof(int));
update = malloc(N_local*sizeof(int)); /* Malloc equation update list */
b_real = malloc(N_local*sizeof(double)); /* Malloc x and b arrays */
b_imag = malloc(N_local*sizeof(double));
x_real = malloc(N_local*sizeof(double));
x_imag = malloc(N_local*sizeof(double));
xx_real = malloc(N_local*sizeof(double));
xx_imag = malloc(N_local*sizeof(double));
for (i=0; i<N_local; i++)
{
val_real[i] = 10 + i/(N_local/10); /* Some very fake diagonals */
val_imag[i] = 10 - i/(N_local/10); /* Should take exactly 20 GMRES steps */
x_real[i] = 0.0; /* Zero initial guess */
x_imag[i] = 0.0;
xx_real[i] = 1.0; /* Let exact solution = 1 */
xx_imag[i] = 0.0;
/* Generate RHS to match exact solution */
b_real[i] = val_real[i]*xx_real[i] - val_imag[i]*xx_imag[i];
b_imag[i] = val_imag[i]*xx_real[i] + val_real[i]*xx_imag[i];
/* All bindx[i] have same value since no off-diag terms */
bindx_real[i] = N_local + 1;
/* each processor owns equations
myPID*N_local through myPID*N_local + N_local - 1 */
update[i] = myPID*N_local + i;
}
bindx_real[N_local] = N_local+1; /* Need this last index */
/* Register Aztec Matrix for Real Part, only imaginary values are needed*/
Amat_real = AZ_matrix_create(N_local);
AZ_set_MSR(Amat_real, bindx_real, val_real, NULL, N_local, update, AZ_GLOBAL);
/* initialize AZTEC options */
AZ_defaults(options, params);
options[AZ_solver] = AZ_gmres; /* Use CG with no preconditioning */
options[AZ_precond] = AZ_none;
options[AZ_kspace] = 21;
options[AZ_max_iter] = 21;
params[AZ_tol] = 1.e-14;
/**************************************************************/
/* Construct linear system. Form depends on input parameters */
/**************************************************************/
/**************************************************************/
/* Method 1: Construct A, x, and b in one call. */
/* Useful if using A,x,b only one time. Equivalent to Method 2*/
/**************************************************************/
AZK_create_linsys_ri2k (x_real, x_imag, b_real, b_imag,
options, params, proc_config,
Amat_real, val_imag, &x, &b, &Amat);
/**************************************************************/
/* Method 2: Construct A, x, and b in separate calls. */
/* Useful for having more control over the construction. */
/* Note that the matrix must be constructed first. */
/**************************************************************/
/* Uncomment these three calls and comment out the above call
AZK_create_matrix_ri2k (options, params, proc_config,
Amat_real, val_imag, &Amat);
AZK_create_vector_ri2k(options, params, proc_config, Amat,
x_real, x_imag, &x);
AZK_create_vector_ri2k(options, params, proc_config, Amat,
b_real, b_imag, &b);
*/
/**************************************************************/
/* Build exact solution vector. */
/* Check residual of init guess and exact solution */
/**************************************************************/
AZK_create_vector_ri2k(options, params, proc_config, Amat,
xx_real, xx_imag, &xx);
residual = AZK_residual_norm(x, b, options, params, proc_config, Amat);
if (proc_config[AZ_node]==0)
printf("\n\n\nNorm of residual using initial guess = %12.4g\n",residual);
residual = AZK_residual_norm(xx, b, options, params, proc_config, Amat);
if (proc_config[AZ_node]==0)
printf("\n\n\nNorm of residual using exact solution = %12.4g\n",residual);
/**************************************************************/
/* Create preconditioner */
/**************************************************************/
AZK_create_precon(options, params, proc_config, x, b, Amat, &Prec);
/**************************************************************/
/* Solve linear system using Aztec. */
/**************************************************************/
AZ_iterate(x, b, options, params, status, proc_config, Amat, Prec, NULL);
/**************************************************************/
/* Extract solution. */
/**************************************************************/
AZK_extract_solution_k2ri(options, params, proc_config, Amat, Prec, x,
x_real, x_imag);
/**************************************************************/
/* Destroy Preconditioner. */
/**************************************************************/
AZK_destroy_precon (options, params, proc_config, Amat, &Prec);
/**************************************************************/
/* Destroy linear system. */
/**************************************************************/
AZK_destroy_linsys (options, params, proc_config, &x, &b, &Amat);
if (proc_config[AZ_node]==0)
{
printf("True residual norm squared = %22.16g\n",status[AZ_r]);
printf("True scaled res norm squared = %22.16g\n",status[AZ_scaled_r]);
printf("Computed res norm squared = %22.16g\n",status[AZ_rec_r]);
}
/* Print comparison between known exact and computed solution */
{double sum = 0.0;
for (i=0; i<N_local; i++) sum += fabs(x_real[i]-xx_real[i]);
for (i=0; i<N_local; i++) sum += fabs(x_imag[i]-xx_imag[i]);
printf(
"Processor %d: Difference between exact and computed solution = %12.4g\n",
proc_config[AZ_node],sum);
}
/* Free memory allocated */
free((void *) val_real );
free((void *) bindx_real );
free((void *) val_imag );
free((void *) update );
free((void *) b_real );
free((void *) b_imag );
free((void *) x_real );
free((void *) x_imag );
free((void *) xx_real );
free((void *) xx_imag );
MPI_Finalize();
return 0 ;
}
 1.8.5
1.8.5