#include <iomanip>
#include <iostream>
#include <stdlib.h>
#include <math.h>
#include "Teuchos_StandardCatchMacros.hpp"
#include "Thyra_VectorStdOps.hpp"
#include "Thyra_DefaultSpmdVectorSpace.hpp"
#include "Thyra_DetachedVectorView.hpp"
#include "VanDerPol_ModelEvaluator_02.hpp"

Functions
int	main (int argc, char *argv[])
	Description: More...

Function Documentation

int main	(	int	argc,
		char *	argv[]
	)

Description:

Example 2: Use ModelEvaluator

The next step in our progression is to use a Thyra::ModelEvaluator for the application problem, i.e., van der Pol Problem, and will provide a common interface to Abstract Numerical Algorithms (ANAs), e.g., nonlinear equations, NOX; stability analysis, LOCA; transient nonlinear ODEs, Tempus; and sensitivity analysis, Sacado. For this example, we will be focusing on setting up a ModelEvaluator for transient nonlinear equations (e.g., explicit and implicit ODEs), and therefore this is not meant to be an indepth tutorial on ModelEvaluators. Please refer to https://docs.trilinos.org/dev/packages/thyra/doc/html/classThyra_1_1ModelEvaluator.html and https://bartlettroscoe.github.io/publications/ModelEvaluator_HPCSW2008.pdf. for additional details on ModelEvaluators.

ModelEvaluator Basics

Because the ModelEvaluator is a generic interface to all the ANAs, the primary function to evaluate the various quantities is simply

Thyra::ModelEvaluator< Scalar >::evalModel(
  const ModelEvaluatorBase::InArgs< Scalar > & inArgs,
  const ModelEvaluatorBase::OutArgs< Scalar > & outArgs ) const

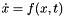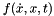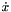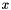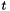where InArgs contains all the required information for the ModelEvaluator to compute the request from the ANA (i.e., Tempus), and OutArgs will contain the computed quantities. In Tempus's case of explicit first-order ODEs ( $\dot{x} = f(x,t)$ ), the InArgs is just $x$ and $t$ and the OutArgs is $\dot{x}$ . For implicit first-order ODEs ( $f(\dot{x},x,t)$ ), the InArgs is $\dot{x}$ , $x$ and $t$ and the OutArgs is the function evaluation, 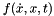$f(\dot{x},x,t)$ . Thus through the InArgs and OutArgs, the ModelEvaluator can determine which evaluation is being requested.

One important attribute of ModelEvaluators is they are stateless! This means they do not storage any information that might change over the duration of the simulation, i.e., the ModelEvaluator does not contain any state information. Any state information must be passed in through the inputs (i.e., InArgs). A simple test for this attribute is the ModelEvaluator will return the exact same evaluation (i.e., OutArgs) for two consecutive evaluations, i.e.,

evalModel(inArgs, outArgs1);

evalModel(inArgs, outArgs2);

and outArgs1 = outArgs2! The stateless attribute is very important for Tempus, because timesteps may fail and need to be retried with a new timestep size. If the ModelEvaluator is not stateless, then the re-evaluation will change! The solvers (e.g., NOX) have a similar issue with multiple evaluations, and also require the stateless attribute.

For details on the ModelEvaluator for the van der Pol Problem implemented in this example, please review VanDerPol_ModelEvaluator_02.

Changes to Use ModelEvaluator

In the following table are code snippets of the changes from the 01_Utilize_Thyra.cpp to 02_Use_ModelEvaluator.cpp. This is similar taking a difference between them for the main() function.

Comments	"Utilize Thyra" Code Snippet	"Use ModelEvaluator" Code Snippet
Construct the ModelEvaluator. The ModelEvaluator, VanDerPol_ModelEvaluator_02, now has all information to construct the problem, including the problem size, vectorLength, parameters, and initial conditions.	// Solution and its time-derivative. int vectorLength = 2; // number state unknowns RCP<const Thyra::VectorSpaceBase<double> > xSpace = Thyra::defaultSpmdVectorSpace<double>(vectorLength);	// Construct ModelEvaluator Teuchos::RCP<const Thyra::ModelEvaluator<double> > model = Teuchos::rcp(new VanDerPol_ModelEvaluator_02<double>());
Get ICs from the ModelEvaluator. The initial conditions (i.e., nominal values) have moved to the VanDerPol_ModelEvaluator_02 constructor, and can retrieved via getNominalValues().	RCP<Thyra::VectorBase<double> > x_n = Thyra::createMember(xSpace); RCP<Thyra::VectorBase<double> > xDot_n = Thyra::createMember(xSpace); // Initial Conditions double time = 0.0; double epsilon = 1.0e-1; { // Scope to delete DetachedVectorViews Thyra::DetachedVectorView<double> x_n_view(x_n); x_n_view[0] = 2.0; x_n_view[1] = 0.0; Thyra::DetachedVectorView<double> xDot_n_view(xDot_n); xDot_n_view[0] = 0.0; xDot_n_view[1] = -2.0/epsilon; }	// Get initial conditions from ModelEvaluator::getNominalValues. RCP<Thyra::VectorBase<double> > x_n = model->getNominalValues().get_x()->clone_v(); RCP<Thyra::VectorBase<double> > xDot_n = model->getNominalValues().get_x_dot()->clone_v();
Setup InArgs and OutArgs for the ModelEvaluator. Before calling evalModel(InArgs, OutArgs), the InArgs and OutArgs need to be setup. For an explicit ODE, we need to set the time, the solution vector, x, and the time derivative, x_dot. In InArgs, x_dot needs to be set to null to indicate it is an explicit ODE evaluation. Finally, we set the outArgs f evaluation to the time derivative, xDot, so it is filled with the result.		// For explicit ODE formulation, xDot = f(x, t), // xDot is part of the outArgs. auto inArgs = model->createInArgs(); auto outArgs = model->createOutArgs(); inArgs.set_t(time); inArgs.set_x(x_n); inArgs.set_x_dot(Teuchos::null); outArgs.set_f(xDot_n);
Evaluate the ModelEvaluator. The righthand-side evaluation is now in the ModelEvaluator, and is called with evalModel(InArgs, OutArgs). Note that xDot has been filled in and can be accessed for the Forward-Euler update.	// Righthand side evaluation and time-derivative at n. { Thyra::ConstDetachedVectorView<double> x_n_view(x_n); Thyra::DetachedVectorView<double> xDot_n_view(xDot_n); xDot_n_view[0] = x_n_view[1]; xDot_n_view[1] = ((1.0-x_n_view[0]x_n_view[0])x_n_view[1]-x_n_view[0])/epsilon; }	// Righthand side evaluation and time-derivative at n. model->evalModel(inArgs, outArgs);

The remainder of 02_Use_ModelEvaluator.cpp is regression testing, etc.

Links

Back to: Tutorials
Previous: Example 1: Utilize Thyra
Next: Example 3: Introduce SolutionState

Definition at line 203 of file 02_Use_ModelEvaluator.cpp.

Functions

Function Documentation

Example 2: Use ModelEvaluator

ModelEvaluator Basics

Changes to Use ModelEvaluator

Links