|
Tempus
Version of the Day
Time Integration
|
|
Tempus
Version of the Day
Time Integration
|
#include <iomanip>#include <iostream>#include <stdlib.h>#include <math.h>#include "Teuchos_StandardCatchMacros.hpp"Go to the source code of this file.
Functions | |
| int | main (int argc, char *argv[]) |
| Description: More... | |
| int main | ( | int | argc, |
| char * | argv[] | ||
| ) |
Description:
This problem is an example of a typical application code before utilizing Tempus, thus it has no Tempus or other Trilinos functionality at this point. It is the starting point to help illustrate the various stages an application can do to take advantage of Tempus's capabilities (additionally see the other Tempus examples).
We have kept the problem itself fairly simple, Van Der Pol problem, with a simple time stepper, Forward Euler, to allow us to focus on the time integration structure and Tempus features as we add them. With this, the implementation is not the most compact or efficient for this simple problem and stepper, but it does have features one would want in a more capable time integrator.
van der Pol problem is a nonlinear electrical circuit, and is a canonical equation of a nonlinear oscillator (Hairer, Norsett, and Wanner, pp. 111-115, and Hairer and Wanner, pp. 4-5) for an electrical circuit. The explicit ODE form, 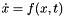 , of the scaled problem is
, of the scaled problem is
![\begin{eqnarray*} \dot{x}_0(t) & = & f_0 = x_1(t) \\ \dot{x}_1(t) & = & f_1 = [(1-x_0^2)x_1-x_0]/\epsilon \end{eqnarray*}](form_448.png)
where the initial conditions are
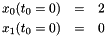
and the initial time derivatives are
![\begin{eqnarray*} \dot{x}_0(t_0=0) & = & x_1(t_0=0) = 0 \\ \dot{x}_1(t_0=0) & = & [(1-x_0^2)x_1-x_0]/\epsilon = -2/\epsilon \end{eqnarray*}](form_399.png)
We will review this program's code structure, 00_Basic_Problem.cpp, and go over its basic details.
| Comments | "Basic Problem" Code Snippet |
|---|---|
| Solution Declaration. One of the first things an application does is to define the solution. | // Solution and its time-derivative.
double x_n[2]; // at time index n
double xDot_n[2]; // at time index n
|
Initial Conditions. Here we are using an array of two doubles for the solution and its time derivative, and set their initial values (see van der Pol Problem). Note that xDot_n is the time derivative, 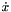 , but is also the right-hand side evaluation, , but is also the right-hand side evaluation, 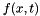 . . | // Initial Conditions
int n = 0;
double time = 0.0;
bool passed = true; // ICs are considered passed.
double epsilon = 1.0e-1;
x_n [0] = 2.0;
x_n [1] = 0.0;
xDot_n[0] = 0.0;
xDot_n[1] = -2.0/epsilon;
|
| Timestep Parameters. The next piece of code sets parameters associated with time-integration, e.g., length of time integration, number of timesteps and the timestep size. | // Timestep size
double finalTime = 2.0;
int nTimeSteps = 2001;
const double constDT = finalTime/(nTimeSteps-1);
|
| Time-Integration Loop. The time-integration loop simply advances the solution until the solution is not "passed", the time has reached the final time, or the number timesteps is reached. | // Advance the solution to the next timestep.
cout << n << " " << time << " " << x_n[0] << " " << x_n[1] << endl;
while (passed && time < finalTime && n < nTimeSteps) {
...
}
|
Initialize the Next Timestep. Within the time loop, we initialize the next timestep, 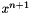 , to the previous timestep, , to the previous timestep, 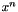 . Although this is not needed in this simple case, if one wants to recover from a failed timestep, the previous timestep, . Although this is not needed in this simple case, if one wants to recover from a failed timestep, the previous timestep, 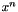 , needs to be perserved until the next timestep is accepted. , needs to be perserved until the next timestep is accepted. | // Initialize next time step
double x_np1[2]; // at time index n+1
x_np1[0] = x_n[0];
x_np1[1] = x_n[1];
|
| Set the Timestep and Time. Although this a constant timestep example, for variable timestepping, the timestep size needs to be determined and the related time for the next timestep set. | // Set the timestep and time.
double dt = constDT;
time = (n+1)*dt;
|
Evaluate Righthand Side Function. This is a simple evaluation of the van der Pol problem and setting it to 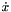 . . | // Righthand side evaluation and time-derivative at n.
xDot_n[0] = x_n[1];
xDot_n[1] = ((1.0 - x_n[0]*x_n[0])*x_n[1] - x_n[0])/epsilon;
|
| Take the Timestep. For Forward Euler, the timestep is a simple daxpy. | // Take the timestep - Forward Euler
x_np1[0] = x_n[0] + dt*xDot_n[0];
x_np1[1] = x_n[1] + dt*xDot_n[1];
|
| Test If Solution is Passing. Here we have a simple test if the solution has passed, i.e., the solution does not have a NAN. Otherwise "promote" the solution to the next timestep and increment the timestep index. | // Test if solution has passed.
if ( std::isnan(x_n[0]) || std::isnan(x_n[1]) ) {
passed = false;
} else {
// Promote to next step (n -> n+1).
x_n[0] = x_np1[0];
x_n[1] = x_np1[1];
n++;
}
|
| Output Solution. Of course, we would like to know that progress of the solution during the simulation. | // Output
if ( n%100 == 0 )
cout << n << " " << time << " " << x_n[0] << " " << x_n[1] << endl;
|
Following the Time-Integration Loop. Following the time loop is some basic regression testing, but serves to show tasks that one may want to complete after completion of time integration.
So this outlines the basic time integration of the van der Pol problem with a few features. We will use this example and introduce Tempus and Trilinos capabilities in the following examples.
Definition at line 217 of file 00_Basic_Problem.cpp.
 1.8.5
1.8.5