#include <Teko_MultPreconditionerFactory.hpp>

Inheritance diagram for Teko::MultPrecsLinearOp:

Public Member Functions
	MultPrecsLinearOp (const Teko::LinearOp &A, const Teko::LinearOp &M1, const Teko::LinearOp &M2)
	Constructor. More...

virtual Teko::VectorSpace	range () const
	Range space of this operator. More...

virtual Teko::VectorSpace	domain () const
	Domain space of this operator. More...

virtual void	implicitApply (const Teko::BlockedMultiVector &r, Teko::BlockedMultiVector &y, const double alpha=1.0, const double beta=0.0) const
	Perform a matrix vector multiply with this implicitly defined blocked operator. More...

Public Member Functions inherited from Teko::BlockImplicitLinearOp
virtual void	implicitApply (const Thyra::EOpTransp M_trans, const BlockedMultiVector &x, BlockedMultiVector &y, const double alpha=1.0, const double beta=0.0) const
	Perform a matrix vector multiply with this implicitly defined blocked operator. More...

Additional Inherited Members
Protected Member Functions inherited from Teko::BlockImplicitLinearOp
virtual bool	opSupportedImpl (const Thyra::EOpTransp M_trans) const
	Functions required by Thyra::LinearOpBase. More...

Detailed Description

Declaration of a Teko::BlockImplicitLinearOp. BlockImplicitLinearOp's are useful when there is no simple or cheap matrix representation of something like f(r). This particular class corresponds to f(r) = (M2 + M1 - M2 * A * M1) r

which is an application of a multiplicative preconditioner. Notice that when M1 = inv(A) or when M2 = inv(A), we get f(r) = inv(A)*r.

While the above matrix represenation could be used instead of writing an implicit function, it requires an additional matrix-vector product than an efficient implementation. It should be noted (see comments below) that there is an efficient matrix represenation of this f(r). Namely,

        f(r) =  [M2 I] [I  -A] [ I]
                       [0   I] [ M1]

so we didn't really need to create an implicit operator.

Definition at line 54 of file Teko_MultPreconditionerFactory.hpp.

Constructor & Destructor Documentation

Teko::MultPrecsLinearOp::MultPrecsLinearOp	(	const Teko::LinearOp &	A,
		const Teko::LinearOp &	M1,
		const Teko::LinearOp &	M2
	)

inline

Constructor.

Definition at line 57 of file Teko_MultPreconditionerFactory.hpp.

Member Function Documentation

virtual Teko::VectorSpace Teko::MultPrecsLinearOp::range ( ) const

inlinevirtual

Range space of this operator.

Implements Teko::BlockImplicitLinearOp.

Definition at line 60 of file Teko_MultPreconditionerFactory.hpp.

virtual Teko::VectorSpace Teko::MultPrecsLinearOp::domain ( ) const

inlinevirtual

Domain space of this operator.

Implements Teko::BlockImplicitLinearOp.

Definition at line 61 of file Teko_MultPreconditionerFactory.hpp.

void Teko::MultPrecsLinearOp::implicitApply	(	const Teko::BlockedMultiVector &	x,
		Teko::BlockedMultiVector &	y,
		const double	alpha = `1.0`,
		const double	beta = `0.0`
	)		const

virtual

Perform a matrix vector multiply with this implicitly defined blocked operator.

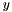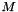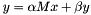
The apply function takes one vector as input and applies a linear operator. The result is returned in $y$ . If this operator is reprsented as $M$ then $y = \alpha M x + \beta y$

Parameters

[in]	x
[in,out]	y
[in]	alpha	(default=1)
[in]	beta	(default=0)

Implements Teko::BlockImplicitLinearOp.

Definition at line 16 of file Teko_MultPreconditionerFactory.cpp.

The documentation for this class was generated from the following files:

Public Member Functions

Additional Inherited Members

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation