|
Stokhos
Development
|
|
Stokhos
Development
|
Class representing a KL expansion of an exponential random field. More...
#include <Stokhos_KL_ExponentialRandomField.hpp>
Public Types | |
|
typedef ExponentialOneDEigenFunction < value_type > | one_d_eigen_func_type |
|
typedef OneDEigenPair < one_d_eigen_func_type > | one_d_eigen_pair_type |
|
typedef ProductEigenPair < one_d_eigen_func_type, execution_space > | product_eigen_pair_type |
|
typedef Kokkos::View < one_d_eigen_func_type **, execution_space > | eigen_func_array_type |
|
typedef Kokkos::View < value_type *, execution_space > | eigen_value_array_type |
Public Member Functions | |
| ExponentialRandomField () | |
| Default constructor. | |
| ExponentialRandomField (Teuchos::ParameterList &solverParams) | |
| Constructor. | |
| KOKKOS_INLINE_FUNCTION | ~ExponentialRandomField () |
| Destructor. | |
| KOKKOS_INLINE_FUNCTION int | spatialDimension () const |
| Return spatial dimension of the field. | |
| KOKKOS_INLINE_FUNCTION int | stochasticDimension () const |
| Return stochastic dimension of the field. | |
| template<typename point_type , typename rv_type > | |
| KOKKOS_INLINE_FUNCTION Teuchos::PromotionTraits < typename rv_type::value_type, value_type >::promote | evaluate (const point_type &point, const rv_type &random_variables) const |
| Evaluate random field at a point. | |
| template<typename point_type > | |
| KOKKOS_INLINE_FUNCTION value_type | evaluate_mean (const point_type &point) const |
| Evaluate mean of random field at a point. | |
| template<typename point_type > | |
| KOKKOS_INLINE_FUNCTION Teuchos::PromotionTraits < typename point_type::value_type, value_type >::promote | evaluate_standard_deviation (const point_type &point) const |
| Evaluate standard deviation of random field at a point. | |
| template<typename point_type > | |
| KOKKOS_INLINE_FUNCTION Teuchos::PromotionTraits < typename point_type::value_type, value_type >::promote | evaluate_eigenfunction (const point_type &point, int i) const |
| Evaluate given eigenfunction at a point. | |
| value_type KOKKOS_INLINE_FUNCTION | eigenvalue (int i) const |
| Return eigenvalue. | |
| void | print (std::ostream &os) const |
| Print KL expansion. | |
Protected Attributes | |
| int | num_KL |
| Number of KL terms. | |
| int | dim |
| Dimension of expansion. | |
| value_type | mean |
| Mean of random field. | |
| value_type | std_dev |
| Standard deviation of random field. | |
| eigen_func_array_type | product_eigen_funcs |
| Product eigenfunctions. | |
| eigen_value_array_type | product_eigen_values |
| Product eigenvalues. | |
Class representing a KL expansion of an exponential random field.
This class provides a means for evaluating a random field 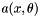 ,
, 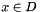 ,
, 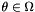 through the KL expansion
through the KL expansion
![\[ a(x,\theta) \approx a_0 + \sigma\sum_{k=1}^M \sqrt{\lambda_k}b_k(x)\xi_k(\theta) \]](form_52.png)
where 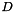 is a
is a 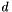 -dimensional hyper-rectangle, for the case when the covariance function of
-dimensional hyper-rectangle, for the case when the covariance function of 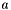 is exponential:
is exponential:
![\[ \mbox{cov}(x,x') = \sigma\exp(-|x_1-x_1'|/L_1-...-|x_d-x_d'|/L_d). \]](form_55.png)
In this case, the covariance function and domain factor into a product 1-dimensional covariance functions over 1-dimensional domains, and thus the eigenfunctions 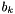 and eigenvalues
and eigenvalues 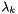 factor into a product of corresponding 1-dimensional eigenfunctions and values. These are computed by the OneDExponentialCovarianceFunction class For a given value of
factor into a product of corresponding 1-dimensional eigenfunctions and values. These are computed by the OneDExponentialCovarianceFunction class For a given value of 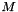 , the code works by computing the
, the code works by computing the 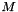 eigenfunctions for each direction using this class. Then all possible tensor products of these one-dimensional eigenfunctions are formed, with corresponding eigenvalue given by the product of the one-dimensional eigenvalues. These eigenvalues are then sorted in increasing order, and the first
eigenfunctions for each direction using this class. Then all possible tensor products of these one-dimensional eigenfunctions are formed, with corresponding eigenvalue given by the product of the one-dimensional eigenvalues. These eigenvalues are then sorted in increasing order, and the first 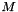 are chosen as the
are chosen as the 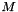 KL eigenpairs. Then given values for the random variables
KL eigenpairs. Then given values for the random variables 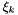 , the class provides a routine for evaluating a realization of the random field.
, the class provides a routine for evaluating a realization of the random field.
The idea for this approach was provided by Chris Miller.
All data is passed into this class through a Teuchos::ParameterList, which accepts the following parameters:
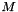 of KL terms
of KL terms 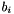 for each dimension
for each dimension 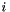
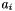 for each dimension
for each dimension 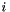
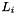 for each dimension
for each dimension 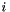
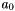 of the random field
of the random field 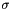 of the random field
of the random field Additionally parameters for the OneDExponentialCovarianceFunction are also accepted.
 1.8.5
1.8.5