|
Stokhos
Development
|
|
Stokhos
Development
|
Abstract base class for multivariate orthogonal polynomials that support computing double and triple products involving derivatives of the basis polynomials. More...
#include <Stokhos_DerivBasis.hpp>
Public Member Functions | |
| DerivBasis () | |
| Constructor. | |
| virtual | ~DerivBasis () |
| Destructor. | |
| virtual Teuchos::RCP < Stokhos::Dense3Tensor < ordinal_type, value_type > > | computeDerivTripleProductTensor (const Teuchos::RCP< const Teuchos::SerialDenseMatrix< ordinal_type, value_type > > &Bij, const Teuchos::RCP< const Stokhos::Sparse3Tensor< ordinal_type, value_type > > &Cijk) const =0 |
Compute triple product tensor 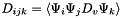 where where 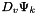 represents the derivative of represents the derivative of 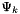 in the direction in the direction 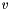 . More... . More... | |
| virtual Teuchos::RCP < Teuchos::SerialDenseMatrix < ordinal_type, value_type > > | computeDerivDoubleProductTensor () const =0 |
Compute double product tensor 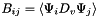 where where 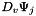 represents the derivative of represents the derivative of 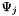 in the direction in the direction 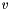 . More... . More... | |
 Public Member Functions inherited from Stokhos::OrthogPolyBasis< ordinal_type, value_type > Public Member Functions inherited from Stokhos::OrthogPolyBasis< ordinal_type, value_type > | |
| OrthogPolyBasis () | |
| Constructor. | |
| virtual | ~OrthogPolyBasis () |
| Destructor. | |
| virtual ordinal_type | order () const =0 |
| Return order of basis. | |
| virtual ordinal_type | dimension () const =0 |
| Return dimension of basis. | |
| virtual ordinal_type | size () const =0 |
| Return total size of basis. | |
| virtual const Teuchos::Array < value_type > & | norm_squared () const =0 |
| Return array storing norm-squared of each basis polynomial. More... | |
| virtual const value_type & | norm_squared (ordinal_type i) const =0 |
Return norm squared of basis polynomial i. | |
| virtual Teuchos::RCP < Stokhos::Sparse3Tensor < ordinal_type, value_type > > | computeTripleProductTensor () const =0 |
| Compute triple product tensor. More... | |
|
virtual Teuchos::RCP < Stokhos::Sparse3Tensor < ordinal_type, value_type > > | computeLinearTripleProductTensor () const =0 |
| Compute linear triple product tensor where k = 0,1. | |
| virtual value_type | evaluateZero (ordinal_type i) const =0 |
Evaluate basis polynomial i at zero. | |
| virtual void | evaluateBases (const Teuchos::ArrayView< const value_type > &point, Teuchos::Array< value_type > &basis_vals) const =0 |
Evaluate basis polynomials at given point point. More... | |
| virtual void | print (std::ostream &os) const =0 |
Print basis to stream os. | |
| virtual const std::string & | getName () const =0 |
| Return string name of basis. | |
Abstract base class for multivariate orthogonal polynomials that support computing double and triple products involving derivatives of the basis polynomials.
|
pure virtual |
Compute double product tensor 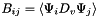 where
where 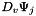 represents the derivative of
represents the derivative of 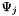 in the direction
in the direction 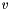 .
.
The definition of 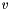 is defined by the derived class implementation.
is defined by the derived class implementation.
Implemented in Stokhos::CompletePolynomialBasis< ordinal_type, value_type >.
|
pure virtual |
Compute triple product tensor 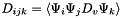 where
where 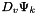 represents the derivative of
represents the derivative of 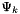 in the direction
in the direction 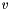 .
.
The definition of 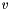 is defined by the derived class implementation.
is defined by the derived class implementation.
Implemented in Stokhos::CompletePolynomialBasis< ordinal_type, value_type >.
 1.8.5
1.8.5