|
Stokhos
Development
|
|
Stokhos
Development
|
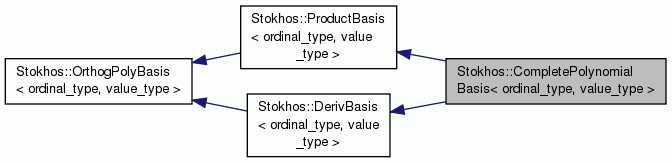
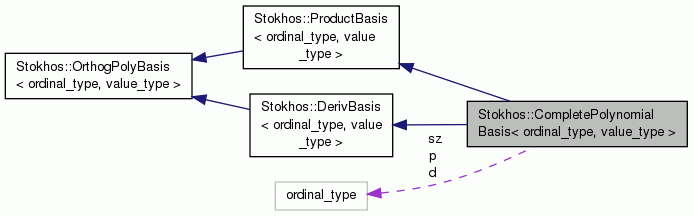
Multivariate orthogonal polynomial basis generated from a total-order complete-polynomial tensor product of univariate polynomials. More...
#include <Stokhos_CompletePolynomialBasis.hpp>
Public Member Functions | |
| CompletePolynomialBasis (const Teuchos::Array< Teuchos::RCP< const OneDOrthogPolyBasis< ordinal_type, value_type > > > &bases, const value_type &sparse_tol=1.0e-12, bool use_old_cijk_alg=false, const Teuchos::RCP< Teuchos::Array< value_type > > &deriv_coeffs=Teuchos::null) | |
| Constructor. More... | |
| virtual | ~CompletePolynomialBasis () |
| Destructor. | |
Implementation of Stokhos::OrthogPolyBasis methods | |
| ordinal_type | order () const |
| Return order of basis. | |
| ordinal_type | dimension () const |
| Return dimension of basis. | |
| virtual ordinal_type | size () const |
| Return total size of basis. | |
| virtual const Teuchos::Array < value_type > & | norm_squared () const |
| Return array storing norm-squared of each basis polynomial. More... | |
| virtual const value_type & | norm_squared (ordinal_type i) const |
Return norm squared of basis polynomial i. | |
| virtual Teuchos::RCP < Stokhos::Sparse3Tensor < ordinal_type, value_type > > | computeTripleProductTensor () const |
| Compute triple product tensor. More... | |
|
virtual Teuchos::RCP < Stokhos::Sparse3Tensor < ordinal_type, value_type > > | computeLinearTripleProductTensor () const |
| Compute linear triple product tensor where k = 0,1,..,d. | |
| virtual value_type | evaluateZero (ordinal_type i) const |
Evaluate basis polynomial i at zero. | |
| virtual void | evaluateBases (const Teuchos::ArrayView< const value_type > &point, Teuchos::Array< value_type > &basis_vals) const |
Evaluate basis polynomials at given point point. More... | |
| virtual void | print (std::ostream &os) const |
Print basis to stream os. | |
| virtual const std::string & | getName () const |
| Return string name of basis. | |
Implementation of Stokhos::ProductBasis methods | |
| virtual const MultiIndex < ordinal_type > & | term (ordinal_type i) const |
Get orders of each coordinate polynomial given an index i. More... | |
| virtual ordinal_type | index (const MultiIndex< ordinal_type > &term) const |
| Get index of the multivariate polynomial given orders of each coordinate. More... | |
| Teuchos::Array< Teuchos::RCP < const OneDOrthogPolyBasis < ordinal_type, value_type > > > | getCoordinateBases () const |
| Return coordinate bases. More... | |
| virtual MultiIndex< ordinal_type > | getMaxOrders () const |
| Return maximum order allowable for each coordinate basis. | |
Implementation of Stokhos::DerivBasis methods | |
| virtual Teuchos::RCP < Stokhos::Dense3Tensor < ordinal_type, value_type > > | computeDerivTripleProductTensor (const Teuchos::RCP< const Teuchos::SerialDenseMatrix< ordinal_type, value_type > > &Bij, const Teuchos::RCP< const Stokhos::Sparse3Tensor< ordinal_type, value_type > > &Cijk) const |
Compute triple product tensor 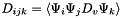 where where 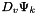 represents the derivative of represents the derivative of 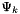 in the direction in the direction 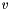 . More... . More... | |
| virtual Teuchos::RCP < Teuchos::SerialDenseMatrix < ordinal_type, value_type > > | computeDerivDoubleProductTensor () const |
Compute double product tensor 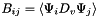 where where 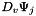 represents the derivative of represents the derivative of 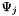 in the direction in the direction 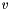 . More... . More... | |
 Public Member Functions inherited from Stokhos::ProductBasis< ordinal_type, value_type > Public Member Functions inherited from Stokhos::ProductBasis< ordinal_type, value_type > | |
| ProductBasis () | |
| Constructor. | |
| virtual | ~ProductBasis () |
| Destructor. | |
 Public Member Functions inherited from Stokhos::OrthogPolyBasis< ordinal_type, value_type > Public Member Functions inherited from Stokhos::OrthogPolyBasis< ordinal_type, value_type > | |
| OrthogPolyBasis () | |
| Constructor. | |
| virtual | ~OrthogPolyBasis () |
| Destructor. | |
 Public Member Functions inherited from Stokhos::DerivBasis< ordinal_type, value_type > Public Member Functions inherited from Stokhos::DerivBasis< ordinal_type, value_type > | |
| DerivBasis () | |
| Constructor. | |
| virtual | ~DerivBasis () |
| Destructor. | |
Protected Types | |
|
typedef Stokhos::CompletePolynomialBasisUtils < ordinal_type, value_type > | CPBUtils |
|
typedef Stokhos::Sparse3Tensor < ordinal_type, value_type > | Cijk_type |
| Short-hand for Cijk. | |
Protected Member Functions | |
|
virtual Teuchos::RCP < Stokhos::Sparse3Tensor < ordinal_type, value_type > > | computeTripleProductTensorOld (ordinal_type order) const |
| Compute triple product tensor using old algorithm. | |
|
virtual Teuchos::RCP < Stokhos::Sparse3Tensor < ordinal_type, value_type > > | computeTripleProductTensorNew (ordinal_type order) const |
| Compute triple product tensor using new algorithm. | |
Protected Attributes | |
| std::string | name |
| Name of basis. | |
| ordinal_type | p |
| Total order of basis. | |
| ordinal_type | d |
| Total dimension of basis. | |
| ordinal_type | sz |
| Total size of basis. | |
|
Teuchos::Array< Teuchos::RCP < const OneDOrthogPolyBasis < ordinal_type, value_type > > > | bases |
| Array of bases. | |
| Teuchos::Array< ordinal_type > | basis_orders |
| Array storing order of each basis. | |
| value_type | sparse_tol |
| Tolerance for computing sparse Cijk. | |
| bool | use_old_cijk_alg |
| Use old algorithm for computing Cijk. | |
|
Teuchos::RCP< Teuchos::Array < value_type > > | deriv_coeffs |
| Coefficients for derivative. | |
| Teuchos::Array< value_type > | norms |
| Norms. | |
|
Teuchos::Array< MultiIndex < ordinal_type > > | terms |
| 2-D array of basis terms | |
| Teuchos::Array< ordinal_type > | num_terms |
| Number of terms up to each order. | |
|
Teuchos::Array< Teuchos::Array < value_type > > | basis_eval_tmp |
| Temporary array used in basis evaluation. | |
Multivariate orthogonal polynomial basis generated from a total-order complete-polynomial tensor product of univariate polynomials.
The multivariate polynomials are given by
![\[ \Psi_i(x) = \psi_{i_1}(x_1)\dots\psi_{i_d}(x_d) \]](form_2.png)
where 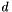 is the dimension of the basis and
is the dimension of the basis and 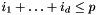 , where
, where 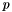 is the order of the basis. The size of the basis is given by
is the order of the basis. The size of the basis is given by 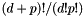 .
.
NOTE: Currently all coordinate bases must be of the samer order 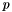 .
.
| Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::CompletePolynomialBasis | ( | const Teuchos::Array< Teuchos::RCP< const OneDOrthogPolyBasis< ordinal_type, value_type > > > & | bases, |
| const value_type & | sparse_tol = 1.0e-12, |
||
| bool | use_old_cijk_alg = false, |
||
| const Teuchos::RCP< Teuchos::Array< value_type > > & | deriv_coeffs = Teuchos::null |
||
| ) |
Constructor.
| bases | array of 1-D coordinate bases |
| sparse_tol | tolerance used to drop terms in sparse triple-product tensors |
| use_old_cijk_alg | use old algorithm for computing the sparse triple product tensor (significantly slower, but simpler) |
| deriv_coeffs | direction used to define derivatives for derivative product tensors. Defaults to all one's if not supplied. |
References Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::bases, Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::basis_eval_tmp, Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::basis_orders, Stokhos::CompletePolynomialBasisUtils< ordinal_type, value_type >::compute_terms(), Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::d, Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::deriv_coeffs, Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::getName(), Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::name, Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::norm_squared(), Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::norms, Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::num_terms, Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::p, Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::sz, and Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::terms.
|
virtual |
Compute double product tensor 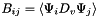 where
where 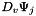 represents the derivative of
represents the derivative of 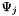 in the direction
in the direction 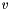 .
.
The definition of 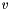 is defined by the
is defined by the deriv_coeffs constructor argument.
Implements Stokhos::DerivBasis< ordinal_type, value_type >.
|
virtual |
Compute triple product tensor 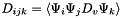 where
where 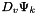 represents the derivative of
represents the derivative of 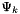 in the direction
in the direction 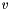 .
.
The definition of 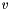 is defined by the
is defined by the deriv_coeffs constructor argument.
Implements Stokhos::DerivBasis< ordinal_type, value_type >.
|
virtual |
Compute triple product tensor.
The 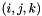 entry of the tensor
entry of the tensor 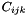 is given by
is given by 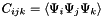 where
where 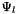 represents basis polynomial
represents basis polynomial 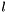 and
and 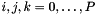 where
where 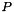 is size()-1.
is size()-1.
Implements Stokhos::OrthogPolyBasis< ordinal_type, value_type >.
|
virtual |
Evaluate basis polynomials at given point point.
Size of returned array is given by size(), and coefficients are ordered from order 0 up to size size()-1.
Implements Stokhos::OrthogPolyBasis< ordinal_type, value_type >.
|
virtual |
Return coordinate bases.
Array is of size dimension().
Implements Stokhos::ProductBasis< ordinal_type, value_type >.
|
virtual |
Get index of the multivariate polynomial given orders of each coordinate.
Given the array term storing  , returns the index
, returns the index 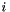 such that
such that 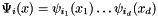 .
.
Implements Stokhos::ProductBasis< ordinal_type, value_type >.
|
virtual |
Return array storing norm-squared of each basis polynomial.
Entry 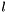 of returned array is given by
of returned array is given by 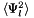 for
for 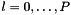 where
where 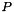 is size()-1.
is size()-1.
Implements Stokhos::OrthogPolyBasis< ordinal_type, value_type >.
Referenced by Stokhos::CompletePolynomialBasis< ordinal_type, value_type >::CompletePolynomialBasis().
|
virtual |
Get orders of each coordinate polynomial given an index i.
The returned array is of size 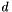 , where
, where 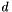 is the dimension of the basis, and entry
is the dimension of the basis, and entry 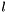 is given by
is given by 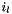 where
where 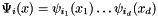 .
.
Implements Stokhos::ProductBasis< ordinal_type, value_type >.
 1.8.5
1.8.5