Implementation of Rythmos::Stepper for explicit Taylor polynomial time integration of ODEs. More...

#include <Rythmos_ExplicitTaylorPolynomialStepper.hpp>

Inheritance diagram for Rythmos::ExplicitTaylorPolynomialStepper< Scalar >:

Public Types
typedef Teuchos::ScalarTraits < Scalar >::magnitudeType	ScalarMag
	Typename of magnitude of scalars. More...

Public Types inherited from Rythmos::InterpolationBufferBase< Scalar >
typedef Teuchos::ScalarTraits < Scalar >::magnitudeType	ScalarMag

Public Member Functions
	ExplicitTaylorPolynomialStepper ()
	Constructor. More...

	~ExplicitTaylorPolynomialStepper ()
	Destructor. More...

RCP< const Thyra::VectorSpaceBase< Scalar > >	get_x_space () const
	Return the space for `x` and `x_dot` More...

void	setModel (const RCP< const Thyra::ModelEvaluator< Scalar > > &model)
	Set model. More...

void	setNonconstModel (const RCP< Thyra::ModelEvaluator< Scalar > > &model)
	Set model. More...

RCP< const Thyra::ModelEvaluator< Scalar > >	getModel () const

RCP< Thyra::ModelEvaluator < Scalar > >	getNonconstModel ()

void	setInitialCondition (const Thyra::ModelEvaluatorBase::InArgs< Scalar > &initialCondition)

Thyra::ModelEvaluatorBase::InArgs < Scalar >	getInitialCondition () const

Scalar	takeStep (Scalar dt, StepSizeType flag)
	Take a time step of magnitude `dt`. More...

const StepStatus< Scalar >	getStepStatus () const

void	setParameterList (RCP< Teuchos::ParameterList > const &paramList)
	Redefined from Teuchos::ParameterListAcceptor. More...

RCP< Teuchos::ParameterList >	getNonconstParameterList ()

RCP< Teuchos::ParameterList >	unsetParameterList ()

RCP< const Teuchos::ParameterList >	getValidParameters () const

std::string	description () const

void	describe (Teuchos::FancyOStream &out, const Teuchos::EVerbosityLevel verbLevel=Teuchos::Describable::verbLevel_default) const

void	addPoints (const Array< Scalar > &time_vec, const Array< RCP< const Thyra::VectorBase< Scalar > > > &x_vec, const Array< RCP< const Thyra::VectorBase< Scalar > > > &xdot_vec)

void	getPoints (const Array< Scalar > &time_vec, Array< RCP< const Thyra::VectorBase< Scalar > > > x_vec, Array< RCP< const Thyra::VectorBase< Scalar > > > xdot_vec, Array< ScalarMag > *accuracy_vec) const
	Get values from buffer. More...

void	setRange (const TimeRange< Scalar > &range, const InterpolationBufferBase< Scalar > &IB)
	Fill data in from another interpolation buffer. More...

TimeRange< Scalar >	getTimeRange () const

void	getNodes (Array< Scalar > *time_vec) const
	Get interpolation nodes. More...

void	removeNodes (Array< Scalar > &time_vec)
	Remove interpolation nodes. More...

int	getOrder () const
	Get order of interpolation. More...

Public Member Functions inherited from Rythmos::StepperBase< Scalar >
virtual bool	supportsCloning () const
	Return if this stepper supports cloning or not. More...

virtual RCP< StepperBase < Scalar > >	cloneStepperAlgorithm () const
	Clone the stepper object if supported. More...

virtual bool	isImplicit () const
	Return if this stepper is an implicit stepper. More...

virtual bool	acceptsModel () const
	Return if this stepper accepts a model. More...

virtual bool	modelIsConst () const
	Return of the model is only const or can be returned as a non-const object. More...

virtual void	setStepControlData (const StepperBase &stepper)
	Set step control data from another stepper. More...

Additional Inherited Members
Related Functions inherited from Rythmos::StepperBase< Scalar >
template<class Scalar >
bool	isInitialized (const StepperBase< Scalar > &stepper)

template<class Scalar >
bool	isInitialized (const StepperBase< Scalar > &stepper)

Related Functions inherited from Rythmos::InterpolationBufferBase< Scalar >
template<class Scalar >
RCP< const Thyra::VectorBase < Scalar > >	get_x (const InterpolationBufferBase< Scalar > &interpBuffer, const Scalar &t)
	Get a single point `x(t)` from an interpolation buffer. More...

template<class Scalar >
RCP< const Thyra::VectorBase < Scalar > >	get_xdot (const InterpolationBufferBase< Scalar > &interpBuffer, const Scalar &t)
	Get a single point `xdot(t)` from an interpolation buffer. More...

template<class Scalar >
void	get_x_and_x_dot (const InterpolationBufferBase< Scalar > &interpBuffer, const Scalar t, const Ptr< RCP< const Thyra::VectorBase< Scalar > > > &x, const Ptr< RCP< const Thyra::VectorBase< Scalar > > > &x_dot)
	Nonmember helper function to get x and x_dot at t. More...

template<class Scalar >
void	assertTimePointsAreSorted (const Array< Scalar > &time_vec)
	Assert that a time point vector is sorted. More...

template<class Scalar >
void	assertNoTimePointsBeforeCurrentTimeRange (const InterpolationBufferBase< Scalar > &interpBuffer, const Array< Scalar > &time_vec, const int &startingTimePointIndex=0)
	Assert that none of the time points fall before the current time range for an interpolation buffer object. More...

template<class Scalar >
void	assertNoTimePointsInsideCurrentTimeRange (const InterpolationBufferBase< Scalar > &interpBuffer, const Array< Scalar > &time_vec)
	Assert that none of the time points fall inside the current time range for an interpolation buffer object. More...

template<class TimeType >
void	selectPointsInTimeRange (const Array< TimeType > &points_in, const TimeRange< TimeType > &range, const Ptr< Array< TimeType > > &points_out)
	Select points from an Array that sit in a TimeRange. More...

template<class TimeType >
void	removePointsInTimeRange (Array< TimeType > *points_in, const TimeRange< TimeType > &range)
	Remove points from an Array that sit in a TimeRange. More...

template<class Scalar >
bool	getCurrentPoints (const InterpolationBufferBase< Scalar > &interpBuffer, const Array< Scalar > &time_vec, Array< RCP< const Thyra::VectorBase< Scalar > > > x_vec, Array< RCP< const Thyra::VectorBase< Scalar > > > xdot_vec, int *nextTimePointIndex)
	Get time points in the current range of an interpolation buffer object. More...

Detailed Description

template<class Scalar>
class Rythmos::ExplicitTaylorPolynomialStepper< Scalar >

Implementation of Rythmos::Stepper for explicit Taylor polynomial time integration of ODEs.

Let

$\frac{dx}{dt} = f(x,t), \quad x(t_0) = a$

be an ODE initial-value problem. This class implements a single time step of an explicit Taylor polynomial time integration method for computing numerical solutions to the IVP. The method consists of computing a local truncated Taylor series solution to the ODE (section Computing the Taylor Polynomial), estimating a step size within the radius of convergence of the Taylor series (section Computing a Step Size) and then summing the polynomial at that step to compute the next point in the numerical integration (section Summing the Polynomial). The algorithmic parameters to the method are controlled through the params argument to the constructor which are described in section Parameters.

Computing the Taylor Polynomial

Let

$x(t) = \sum_{k=0}^\infty x_k (t-t_0)^k$

be a power series solution to the IVP above. Then 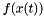$f(x(t))$ can be expaned in a power series along the solution curve $x(t)$ :

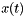$f(x(t),t) = \sum_{k=0}^\infty f_k (t-t_0)^k$

where

$f_k = \left.\frac{1}{k!}\frac{d^k}{dt^k} f(x(t),t)\right|_{t=t_0}.$

By differentiating the power series for 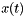$x(t)$ to compute a power series for 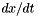$dx/dt$ and then comparing coefficients in the equation 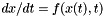$dx/dt=f(x(t),t)$ we find the following recurrence relationship for the Taylor coefficients $\{x_k\}$ :

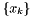$x_{k+1} = \frac{1}{k+1} f_k, \quad k=0,1,\dots$

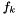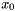where each coefficient $f_k$ is a function only of $x_0,\dots,x_k$ and can be efficiently computed using the Taylor polynomial mode of automatic differentation. This allows the Taylor coefficients to be iteratively computed starting with the initial point $x_0$ up to some fixed degree 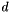$d$ to yield a local truncated Taylor polynomial approximating the solution to the IVP.

Computing a Step Size

With the truncated Taylor polynomial solution 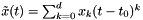$\tilde{x}(t) = \sum_{k=0}^d x_k (t-t_0)^k$ in hand, a step size is chosen by estimating the truncation error in the polynomial solution and forcing this error to be less than some prescribed tolerance. Let

$\rho = \max_{d/2\leq k\leq d} (1+\|x_k\|_\infty)^{1/k}$

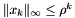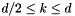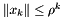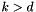so $\|x_k\|_\infty\leq\rho^k$ for $d/2\leq k \leq d$ . Assume $\|x_k\|\leq\rho^k$ for $k>d$ as well, then for any 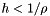$h<1/\rho$ it can be shown that the truncation error is bounded by

$\frac{(\rho h)^{d+1}}{1-\rho h}.$

A step size 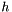$h$ is then given by

$h = \exp\left(\frac{1}{d+1}\log\varepsilon-\log\rho\right)$

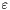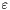for some error tolerance $\varepsilon$ given an error of approximatly $\varepsilon$ .

Summing the Polynomial

With a step size 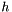$h$ computed,

$x^\ast = \sum_{k=0}^d x_k h^k$

is used as the next integration point where a new Taylor series is calculated. Local error per step can also be controlled by computing 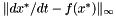$\|dx^\ast/dt - f(x^\ast)\|_\infty$ . If this error is too large, the step size can be reduced to an appropriate size.

Parameters

This method recognizes the following algorithmic parameters that can be set in the params argument to the constructor:

"Initial Time" (Scalar) [Default = 0] Initial integration time
"Final Time" (Scalar) [Default = 1] Final integration time
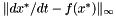"Local Error Tolerance" (Magnitude) [Default = 1.0e-10] Error tolerance on $\|dx^\ast/dt - f(x^\ast)\|_\infty$ as described above.
"Minimum Step Size" (Scalar) [Default = 1.0e-10] Minimum step size
"Maximum Step Size" (Scalar) [Default = 1.0] Maximum step size
"Taylor Polynomial Degree" (int) [Default = 40] Degree of local Taylor polynomial approximation.

Definition at line 163 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

Member Typedef Documentation

template<class Scalar>

typedef Teuchos::ScalarTraits<Scalar>::magnitudeType Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::ScalarMag

Typename of magnitude of scalars.

Definition at line 168 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

Constructor & Destructor Documentation

template<class Scalar >

Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::ExplicitTaylorPolynomialStepper ( )

Constructor.

Definition at line 364 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar >

Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::~ExplicitTaylorPolynomialStepper ( )

Destructor.

Definition at line 372 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

Member Function Documentation

template<class Scalar >

RCP< const Thyra::VectorSpaceBase< Scalar > > Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::get_x_space ( ) const

virtual

Return the space for x and x_dot

Implements Rythmos::InterpolationBufferBase< Scalar >.

Definition at line 863 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar>

void Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::setModel ( const RCP< const Thyra::ModelEvaluator< Scalar > > & model )

virtual

Set model.

Implements Rythmos::StepperBase< Scalar >.

Definition at line 406 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar>

void Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::setNonconstModel ( const RCP< Thyra::ModelEvaluator< Scalar > > & model )

virtual

Set model.

Implements Rythmos::StepperBase< Scalar >.

Definition at line 419 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar >

RCP< const Thyra::ModelEvaluator< Scalar > > Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::getModel ( ) const

virtual

Implements Rythmos::StepperBase< Scalar >.

Definition at line 429 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar >

RCP< Thyra::ModelEvaluator< Scalar > > Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::getNonconstModel ( )

virtual

Implements Rythmos::StepperBase< Scalar >.

Definition at line 437 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar>

void Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::setInitialCondition ( const Thyra::ModelEvaluatorBase::InArgs< Scalar > & initialCondition )

virtual

Implements Rythmos::StepperBase< Scalar >.

Definition at line 444 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar >

Thyra::ModelEvaluatorBase::InArgs< Scalar > Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::getInitialCondition ( ) const

virtual

Implements Rythmos::StepperBase< Scalar >.

Definition at line 467 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar>

Scalar Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::takeStep	(	Scalar	dt,
		StepSizeType	flag
	)

virtual

Take a time step of magnitude dt.

Implements Rythmos::StepperBase< Scalar >.

Definition at line 475 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar >

const StepStatus< Scalar > Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::getStepStatus ( ) const

virtual

Implements Rythmos::StepperBase< Scalar >.

Definition at line 593 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar >

void Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::setParameterList ( RCP< Teuchos::ParameterList > const & paramList )

Redefined from Teuchos::ParameterListAcceptor.

Definition at line 626 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar >

RCP< Teuchos::ParameterList > Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::getNonconstParameterList ( )

Definition at line 661 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar >

RCP< Teuchos::ParameterList > Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::unsetParameterList ( )

Definition at line 669 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar >

RCP< const Teuchos::ParameterList > Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::getValidParameters ( ) const

Definition at line 679 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar >

std::string Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::description ( ) const

Definition at line 701 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar >

void Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::describe	(	Teuchos::FancyOStream &	out,
		const Teuchos::EVerbosityLevel	verbLevel = `Teuchos::Describable::verbLevel_default`
	)		const

Definition at line 709 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar>

void Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::addPoints	(	const Array< Scalar > &	time_vec,
		const Array< RCP< const Thyra::VectorBase< Scalar > > > &	x_vec,
		const Array< RCP< const Thyra::VectorBase< Scalar > > > &	xdot_vec
	)

virtual

Redefined from InterpolationBufferBase Add points to buffer

Implements Rythmos::InterpolationBufferBase< Scalar >.

Definition at line 741 of file Rythmos_ExplicitTaylorPolynomialStepper.hpp.

template<class Scalar>

void Rythmos::ExplicitTaylorPolynomialStepper< Scalar >::getPoints	(	const Array< Scalar > &	time_vec,
		Array< RCP< const Thyra::VectorBase< Scalar > > > *	x_vec,
		Array< RCP< const Thyra::VectorBase< Scalar > > > *	xdot_vec,
		Array< ScalarMag > *	accuracy_vec
	)		const