Concrete implementation class for a matrix vertically concatonated with an identity matrix. More...

#include <ConstrainedOptPack_MatrixIdentConcatStd.hpp>

Inheritance diagram for ConstrainedOptPack::MatrixIdentConcatStd:

Public types
enum	ETopBottom

typedef Teuchos::RCP< const MatrixOp >	D_ptr_t

Constructors/initializers.
	MatrixIdentConcatStd ()
	Constructs to uninitialized. More...

virtual void	initialize (const VectorSpace::space_ptr_t &space_cols, const VectorSpace::space_ptr_t &space_rows, ETopBottom top_or_bottom, value_type alpha, const D_ptr_t &D_ptr, BLAS_Cpp::Transp D_trans)
	Setup with a matrix object. More...

virtual void	set_uninitialized ()
	Set the matrix to uninitialized. More...

virtual const D_ptr_t &	D_ptr () const
	Return the smart reference counted point to the `D` matrix. More...

Overridden form MatrixIdentConcat
Range1D	D_rng () const

Range1D	I_rng () const

value_type	alpha () const

const MatrixOp &	D () const

BLAS_Cpp::Transp	D_trans () const

Overridden from MatrixOp
const VectorSpace &	space_cols () const

const VectorSpace &	space_rows () const

MatrixOp &	operator= (const MatrixOp &m)
	The default just performs a shallow copy and just copies the underlying smart reference counted pointer. If other behavior is desired then this method must be overridden. More...

Detailed Description

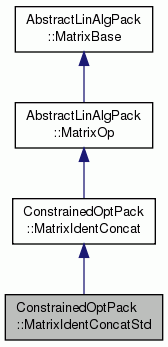
Concrete implementation class for a matrix vertically concatonated with an identity matrix.

Represents an interface for a matrix that represents:

M = [ alpha*op(D) ]    (TOP)
    [     I       ]

or

M = [     I       ]
    [ alpha*op(D) ]   (BOTTOM)

This subclass allows a client to set the representation matrix D.

Definition at line 67 of file ConstrainedOptPack_MatrixIdentConcatStd.hpp.

Member Typedef Documentation

typedef Teuchos::RCP<const MatrixOp> ConstrainedOptPack::MatrixIdentConcatStd::D_ptr_t

Definition at line 75 of file ConstrainedOptPack_MatrixIdentConcatStd.hpp.

Member Enumeration Documentation

enum ConstrainedOptPack::MatrixIdentConcatStd::ETopBottom

Definition at line 73 of file ConstrainedOptPack_MatrixIdentConcatStd.hpp.

Constructor & Destructor Documentation

ConstrainedOptPack::MatrixIdentConcatStd::MatrixIdentConcatStd ( )

Constructs to uninitialized.

Definition at line 51 of file ConstrainedOptPack_MatrixIdentConcatStd.cpp.

Member Function Documentation

void ConstrainedOptPack::MatrixIdentConcatStd::initialize	(	const VectorSpace::space_ptr_t &	space_cols,
		const VectorSpace::space_ptr_t &	space_rows,
		ETopBottom	top_or_bottom,
		value_type	alpha,
		const D_ptr_t &	D_ptr,
		BLAS_Cpp::Transp	D_trans
	)

virtual

Setup with a matrix object.

Parameters

top_or_bottom	[in] If `TOP` then `M = [ alphaop(D); I ]` and if `BOTTOM` then `M = [ I; alphaop(D) ]`
alpha	[in] Scalar that multiplies `op(D)`
D_ptr	[in] Smart pointer to a matrix object that represents `D`. The matrix object pointed to must not be altered until `this` object is no longer in use or `this->set_uninitialized()` has been called.
D_trans	[in] Determines if `op(D) = D` (`no_trans#`) or `op(D) = D'` (`trans`).

Preconditions:

D.get() != NULL (throw std::invalid_argument)
space_cols->dim() == rows(op(D)) + cols(op(D)) (throw std::invalid_argument)
space_rows->dim() == cols(op(D)) (throw std::invalid_argument)
space_cols->sub_space(D_rng)->is_compatible(op(D).space_cols()) (throw std::invalid_argument) See D_rng defined below
space_rows->is_compatible(op(D).space_rows()) (throw std::invalid_argument)

Postconditions:

this->D_ptr().get() == D_ptr.get()
&this->D() == this->D_ptr().get()
this->D_trans() == D_trans
this->alpha() == alpha
this->rows() == rows(op(D)) + cols(op(D))
this->cols() == cols(op(D))
&this->space_cols() == space_cols.get()
&this->space_rows() == space_rows.get()
[top_or_bottom == TOP] this->D_rng() = [1,rows(op(D))]
[top_or_bottom == TOP] this->I_rng() = [rows(op(D))+1,rows(op(D))+cols(op(D))]
[top_or_bottom == BOTTOM] this->D_rng() = [cols(op(D))+1,rows(op(D))+cols(op(D))]
[top_or_bottom == BOTTOM] this->I_rng() = [1,cols(op(D))]

Definition at line 56 of file ConstrainedOptPack_MatrixIdentConcatStd.cpp.

void ConstrainedOptPack::MatrixIdentConcatStd::set_uninitialized ( )

virtual

Set the matrix to uninitialized.

Postconditions:

this->space_cols() throws an exception
this->space_rows() throws an exception
this->D_ptr().get() == NULL
&this->D() throws an exception
this->D_trans() == no_trans
this->alpha() == 0.0
this->rows() == 0
this->cols() == 0
[top_or_bottom == TOP] this->D_rng() = [1,rows(op(D))]
[top_or_bottom == TOP] this->I_rng() = [rows(op(D))+1,rows(op(D))+cols(op(D))]
[top_or_bottom == BOTTOM] this->D_rng() = [cols(op(D))+1,rows(op(D))+cols(op(D))]
[top_or_bottom == BOTTOM] this->I_rng() = [1,cols(op(D))]

Definition at line 94 of file ConstrainedOptPack_MatrixIdentConcatStd.cpp.

const MatrixIdentConcatStd::D_ptr_t & ConstrainedOptPack::MatrixIdentConcatStd::D_ptr ( ) const

virtual

Return the smart reference counted point to the D matrix.

If the matrix object D is owned exclusively by this matrix object then this->D_ptr().count() == 1 on return.

Definition at line 106 of file ConstrainedOptPack_MatrixIdentConcatStd.cpp.

Range1D ConstrainedOptPack::MatrixIdentConcatStd::D_rng ( ) const

virtual

Implements ConstrainedOptPack::MatrixIdentConcat.

Range1D ConstrainedOptPack::MatrixIdentConcatStd::I_rng ( ) const

virtual

Implements ConstrainedOptPack::MatrixIdentConcat.

value_type ConstrainedOptPack::MatrixIdentConcatStd::alpha ( ) const

virtual

Implements ConstrainedOptPack::MatrixIdentConcat.

Definition at line 123 of file ConstrainedOptPack_MatrixIdentConcatStd.cpp.

const MatrixOp& ConstrainedOptPack::MatrixIdentConcatStd::D ( ) const

virtual

Implements ConstrainedOptPack::MatrixIdentConcat.

BLAS_Cpp::Transp ConstrainedOptPack::MatrixIdentConcatStd::D_trans ( ) const

virtual

Implements ConstrainedOptPack::MatrixIdentConcat.

Definition at line 133 of file ConstrainedOptPack_MatrixIdentConcatStd.cpp.

const VectorSpace& ConstrainedOptPack::MatrixIdentConcatStd::space_cols ( ) const

virtual

Implements AbstractLinAlgPack::MatrixBase.

const VectorSpace& ConstrainedOptPack::MatrixIdentConcatStd::space_rows ( ) const

virtual

Implements AbstractLinAlgPack::MatrixBase.

MatrixOp & ConstrainedOptPack::MatrixIdentConcatStd::operator= ( const MatrixOp & m )

The default just performs a shallow copy and just copies the underlying smart reference counted pointer. If other behavior is desired then this method must be overridden.

Definition at line 150 of file ConstrainedOptPack_MatrixIdentConcatStd.cpp.

The documentation for this class was generated from the following files:

Public types

Constructors/initializers.

Overridden form MatrixIdentConcat

Overridden from MatrixOp

Detailed Description

Member Typedef Documentation

Member Enumeration Documentation

Constructor & Destructor Documentation

Member Function Documentation