|
AbstractLinAlgPack: C++ Interfaces For Vectors, Matrices And Related Linear Algebra Objects
Version of the Day
|
|
AbstractLinAlgPack: C++ Interfaces For Vectors, Matrices And Related Linear Algebra Objects
Version of the Day
|
Interface for the creation and maintainance of a basis matrix for a decomposition of linearlized constriants. More...
#include <AbstractLinAlgPack_BasisSystem.hpp>
Classes | |
| class | SingularBasis |
Public Member Functions | |
| BasisSystem (const mat_sym_fcty_ptr_t &factory_transDtD, const mat_sym_nonsing_fcty_ptr_t &factory_S) | |
Required constructor (calls initialize()). More... | |
| virtual void | initialize (const mat_sym_fcty_ptr_t &factory_transDtD, const mat_sym_nonsing_fcty_ptr_t &factory_S) |
Initialize the factory objects for the special matrices for D'*D and S = I + D'*D. More... | |
| virtual | ~BasisSystem () |
Public types | |
| enum | EMatRelations |
| typedef Teuchos::RCP< const Teuchos::AbstractFactory < MatrixOpNonsing > > | mat_nonsing_fcty_ptr_t |
| typedef Teuchos::RCP< const Teuchos::AbstractFactory < MatrixOp > > | mat_fcty_ptr_t |
| typedef Teuchos::RCP< const Teuchos::AbstractFactory < MatrixSymOp > > | mat_sym_fcty_ptr_t |
| typedef Teuchos::RCP< const Teuchos::AbstractFactory < MatrixSymOpNonsing > > | mat_sym_nonsing_fcty_ptr_t |
Matrix factories | |
| virtual const mat_nonsing_fcty_ptr_t | factory_C () const =0 |
Return a matrix factory object for basis C = [ Gc(var_dep,equ_decomp)'; Gh(var_dep,inequ_decomp)' ]. More... | |
| virtual const mat_fcty_ptr_t | factory_D () const =0 |
Return a matrix factory object for sensitivity matrix D = -inv(C)*N. More... | |
| virtual const mat_fcty_ptr_t | factory_GcUP () const |
Return a matrix factory object for auxiliary sensitivity matrix GcUP = Gc(var_indep,equ_undecomp)' + Gc(var_dep,equ_undecomp)'*D. More... | |
| virtual const mat_sym_fcty_ptr_t | factory_transDtD () const |
Returns a matrix factory for the result of J = D'*D More... | |
| virtual const mat_sym_nonsing_fcty_ptr_t | factory_S () const |
Returns a matrix factory for the result of S = I + D'*D More... | |
Return the ranges for variable and constraint partitioning | |
| virtual Range1D | var_dep () const =0 |
| Range of dependent (basic) variables. More... | |
| virtual Range1D | var_indep () const =0 |
| Range of independnet (nonbasic) variables. More... | |
| virtual Range1D | equ_decomp () const |
| Range of decomposed general equality constraints. More... | |
| virtual Range1D | equ_undecomp () const |
| Range of undecomposed general equality constriants. More... | |
Update matrices | |
| virtual void | update_basis (const MatrixOp &Gc, MatrixOpNonsing *C, MatrixOp *D, MatrixOp *GcUP, EMatRelations mat_rel=MATRICES_INDEP_IMPS, std::ostream *out=NULL) const =0 |
| Update a basis and posssibly the direct sensitivity matrix for a set of Jacobian matrices. More... | |
Interface for the creation and maintainance of a basis matrix for a decomposition of linearlized constriants.
Overview:
This interface is designed to take the Jacobian for a sub-set of equality constraints 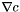 and to create a basis matrix. Assume we have the folloing linealrized equality constraints:
and to create a basis matrix. Assume we have the folloing linealrized equality constraints:
![\[ \nabla c^T d + c = 0 \]](form_1.png)
The C++ identifier given to 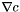 is
is Gc.
In this basis interface we will assume that d, c and h are sorted such that we define the following sets (given the partitioning matrices ![$ Q_{x} = \left[\begin{array}{c} Q_{xD} \\ Q_{xI} \end{array}\right] $](form_2.png) ,
, ![$ Q_{c} = \left[\begin{array}{c} Q_{cD} \\ Q_{cU} \end{array}\right] $](form_3.png) , ):
, ):
d(var_dep) ( 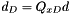 ) : Dependent (i.e. basis) variables.
) : Dependent (i.e. basis) variables. d(var_indep) ( 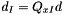 ) : Independent (i.e. nonbasic) variables.
) : Independent (i.e. nonbasic) variables. c(equ_decomp) ( 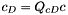 ) : Decomposed equality constriants.
) : Decomposed equality constriants. c(equ_undecomp) ( 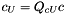 ): Undecomposed equality constriants.
): Undecomposed equality constriants. Given these partitionings we can define a basis matrix C for the following Jacobian sub-matrices (in mathematical and Matlab-like notation):
![\[ C = Q_{cD} \nabla c_T (Q_{xD})^T \]](form_8.png)
C = Gc(var_dep,equ_decomp)'
We can also define a nonbasis matrix N for the decomposed constraints as:
![\[ N = Q_{cD} \nabla c^T (Q_{xI})^T \]](form_9.png)
N = Gc(var_indep,equ_decomp)'
Given the definitions of C and N above, we can define the following direct-sensitivity matrix D:
![\[ D = - C^{-1} N \]](form_10.png)
D = -inv(C)*N
Given this matrix D, we can define another projected sensistivity matrix:
GcUP = Gc(var_indep,equ_undecomp)' + Gc(var_dep,equ_undecomp)' * D This interface allows a client to create the basis matrix C and optionally the direct sensitivity matrix D = -inv(C)*N and the auxiliary projected sensistivity matrix GcUP (shown above). These matrix objects are independent from this BasisSystem object or from other C, D, or GcUP objects. Therefore, a BasisSystem object can be thought of as an "Abstract Factory" for basis matrices and auxillary matrices. Note that a BasisSystem object will not compute the matrices D, GcUP unless specifically asked.
Note that the purpose of this interface is to abstract client code away from the details of how the matrix Gc is represented and implemented and how the basis matrix C is formed and implemented. The complexity of these matrices could vary from simple dense serial matrices all the way up massively parallel matrices using iterative solvers for C running on computers with thousands of nodes.
This interface also allows clients to compute the matrices J = D'*D and S = I + D'*D.
Client usage:
The matrix objects for C, D, GcUP, D'*D and S=I+D'*D are created by the client using the AbstractFactory<> objects returned from factory_C(), factory_D(), factory_GcUP(), factory_transDtD() and factory_S() respectively. These methods return smart pointers to these matrix factory objects and these objects are ment to have a lifetime that extends up to and beyond the lifetime of the BasisSystem object that created them. Note that the matrix objects returned by these matrix factory objects are not to be considered usable until they have passed through update_basis() or receive some other appropriate initialization.
The ranges of the dependent and independent variables, and decomposed and undecomposed equality constriants are returned by the methods var_dep(), var_indep(), equ_decomp() andequ_undecomp() respectively. There are a few obvious assertions for the values that these ranges can take on. Assuming that Gc is non-null when passed to update_basis(), the following assertions apply:
var_dep().size() == equ_decomp().size() + inequ_decomp().size() var_dep().size() + var_indep().size() == Gc.rows() equ_decomp().size() + equ_undecomp().size() == Gc.cols() Note that the client should not rely on var_dep(), var_indep(), equ_decomp(), or equ_undecomp() until after the first call to update_basis(). This allows a BasisSystem object to adjust itself to accommodate the input matrix Gc.
A fully initialized BasisSystem object will be setup to work with specific types and sizes of input matrices Gc and Gh. Therefore, the client should be able to get accrate values from var_dep(), var_indep(), equ_decomp(), or equ_undecomp() even before the first call to update_basis(). The BasisSystem object must therefore be initialized in some way to accommodate input matrices Gc and Gh of a specific dimension.
Note that This interface is completely worthless unless var_dep() returns some valid range (i.e. a basis matrix exists). If var_dep().size() == 0 then this is an indication that this is uninitialzed and therefore only the factory methods can be called!
The method update_basis() is used by the client to update the basis matrix C and perhaps the direct sensitivity matrix D and it's auxillary projected sensistivity matrix GcUP Strictly speaking, it would be possible to form the matrix D externally through the MatrixNonsing interface using the returned C and an N matrix object, but this may not take advantage of any special application specific tricks that can be used to form D. Note that this interface does not return a nonbasis matrix object for N. However, this matrix object will be needed for an implicit D matrix object that the client will undoubtably want to create. Creating such a matrix object is simple given the method MatrixOp::sub_view(). The following code example shows how to create a matrix object for N (given the matrix Gc input to bs.update_basis(Gc,...) and bs):
Given the nonbasis matrix object for N returned by the above function, this matrix object could be used to form an explicit D matrix object (but perhaps not very efficiently) or be used to implicitly implement matrix vector products with D as:
op(D)*v = op(-inv(C)*N)*v = -inv(C)*(N*v) or -N'*(inv(C')*v)
The client can also form matrices of the form S = I + D'*D as follows:
The matrix S must then be fully initialized and ready to go.
Subclass developer's notes:
The default implementation (of the methods that have default implementations) assume that there are no undecomposed equality constriants.
ToDo: Finish documentation!
Definition at line 228 of file AbstractLinAlgPack_BasisSystem.hpp.
| typedef Teuchos::RCP< const Teuchos::AbstractFactory<MatrixOpNonsing> > AbstractLinAlgPack::BasisSystem::mat_nonsing_fcty_ptr_t |
Definition at line 236 of file AbstractLinAlgPack_BasisSystem.hpp.
| typedef Teuchos::RCP< const Teuchos::AbstractFactory<MatrixOp> > AbstractLinAlgPack::BasisSystem::mat_fcty_ptr_t |
Definition at line 239 of file AbstractLinAlgPack_BasisSystem.hpp.
| typedef Teuchos::RCP< const Teuchos::AbstractFactory<MatrixSymOp> > AbstractLinAlgPack::BasisSystem::mat_sym_fcty_ptr_t |
Definition at line 242 of file AbstractLinAlgPack_BasisSystem.hpp.
| typedef Teuchos::RCP< const Teuchos::AbstractFactory<MatrixSymOpNonsing> > AbstractLinAlgPack::BasisSystem::mat_sym_nonsing_fcty_ptr_t |
Definition at line 245 of file AbstractLinAlgPack_BasisSystem.hpp.
Definition at line 250 of file AbstractLinAlgPack_BasisSystem.hpp.
| AbstractLinAlgPack::BasisSystem::BasisSystem | ( | const mat_sym_fcty_ptr_t & | factory_transDtD, |
| const mat_sym_nonsing_fcty_ptr_t & | factory_S | ||
| ) |
Required constructor (calls initialize()).
Definition at line 47 of file AbstractLinAlgPack_BasisSystem.cpp.
|
inlinevirtual |
Definition at line 274 of file AbstractLinAlgPack_BasisSystem.hpp.
|
virtual |
Initialize the factory objects for the special matrices for D'*D and S = I + D'*D.
Postconditions:
Definition at line 55 of file AbstractLinAlgPack_BasisSystem.cpp.
|
pure virtual |
Return a matrix factory object for basis C = [ Gc(var_dep,equ_decomp)'; Gh(var_dep,inequ_decomp)' ].
Implemented in AbstractLinAlgPack::BasisSystemComposite, and AbstractLinAlgPack::BasisSystemPermDirectSparse.
|
pure virtual |
Return a matrix factory object for sensitivity matrix D = -inv(C)*N.
It is allowed for this to return NULL in which case update_basis() will not accept a D matrix to be computed.
Implemented in AbstractLinAlgPack::BasisSystemComposite, and AbstractLinAlgPack::BasisSystemPermDirectSparse.
|
virtual |
Return a matrix factory object for auxiliary sensitivity matrix GcUP = Gc(var_indep,equ_undecomp)' + Gc(var_dep,equ_undecomp)'*D.
It is allowed for this to return NULL in which case update_basis() will not accept a GcUP matrix to be computed.
Reimplemented in AbstractLinAlgPack::BasisSystemPermDirectSparse.
Definition at line 75 of file AbstractLinAlgPack_BasisSystem.cpp.
|
virtual |
Returns a matrix factory for the result of J = D'*D
The resulting matrix is symmetric but is assumed to be singular.
Postconditions:
AbstractLinAlgPack::syrk(D,trans,alpha,beta,return->create().get()) must not throw an exception once D has been initialized by this. Definition at line 81 of file AbstractLinAlgPack_BasisSystem.cpp.
|
virtual |
Returns a matrix factory for the result of S = I + D'*D
The resulting matrix is symmetric and is guarrenteed to be nonsingular.
Postconditions:
dynamic_cast<MatrixSymInitDiag*>(return->create().get()) != NULL Definition at line 87 of file AbstractLinAlgPack_BasisSystem.cpp.
|
pure virtual |
Range of dependent (basic) variables.
If there are no dependent variables then return.size() == 0. This would be a strange case where there was no basis matrix in which case this whole interface would be worthless. Therefore, to be useful return.size() > 0 must be true.
If var_dep().size() returns 0, then this is an indication that *this is uninitialized and only the factory methods can be called.
Implemented in AbstractLinAlgPack::BasisSystemComposite, and AbstractLinAlgPack::BasisSystemPermDirectSparse.
|
pure virtual |
Range of independnet (nonbasic) variables.
It is possible that the basis matrix may take up all of the degrees of freedom with var_dep().size() == Gc->rows(). In this case, there is no nonbasis matrix N and no direct sensitivity matrix D. In this case return.size() == 0. In the more general case however, return.size() > 0.
Implemented in AbstractLinAlgPack::BasisSystemComposite, and AbstractLinAlgPack::BasisSystemPermDirectSparse.
|
virtual |
Range of decomposed general equality constraints.
If there are no decomposed general equality constriants then return.size() == 0. Otherwise, return.size() > 0.
The default implementation return Range1D(1,this->var_dep().size())
Reimplemented in AbstractLinAlgPack::BasisSystemPermDirectSparse.
Definition at line 64 of file AbstractLinAlgPack_BasisSystem.cpp.
|
virtual |
Range of undecomposed general equality constriants.
If there are no undecomposed equality constriants then return.size() == 0. Otherwise, return.size() > 0.
The default implementation return Range1D::Invalid
Reimplemented in AbstractLinAlgPack::BasisSystemPermDirectSparse.
Definition at line 70 of file AbstractLinAlgPack_BasisSystem.cpp.
|
pure virtual |
Update a basis and posssibly the direct sensitivity matrix for a set of Jacobian matrices.
| Gc | [in] Jacobian of the equality constriants. |
| C | [out] Basis matrix. If C == NULL on input, then this quantity is not updated. If C != NULL then this must have been created by this->factory_C()->create(). This basis matrix object must be independent of the input matrices Gc and/or Gh. Therefore, it must be legal to destroy Gc and/or Gh without affecting the behavior of the basis matrix object C. |
| D | [out] Direct sensitivity matrix D = -inv(C)*N. If D == NULL on input then this quantity is not updated. If D != NULL then this must have been created by this->factory_D()->create(). This matrix object is meaningless if this->var_indep() == Range1D::Invalid on return. This matrix object must be independent matrices Gc and/or Gh Therefore, it must be legal to destroy Gc and/or Gh without affecting the behavior of the direct sensitivity matrix object D. |
| GcUP | [out] Auxiliary sensistivity matrix GcUP = Gc(var_indep,equ_undecomp)' + Gc(var_dep,equ_undecomp)'*D. If GcUP == NULL on input then this quantity is not updated. If GcUP != NULL then this must have been created by this->factory_GcUP()->create(). This matrix object is meaningless if this->var_indep() == Range1D::Invalid on return. This matrix object must be independent of the matrices Gc and/or Gh and/or D. Therefore, it must be legal to destroy Gc and/or Gh and/or D without affecting the behavior of the matrix object GcUP. |
| mat_rel | [in] Determines if the matrix objects must be completely independent or not.
|
| out | [in/out] If out!=NULL, then some information about the operations performed internally may be printed to *out. The amount of this output should be very minimal and should not significantly increase with the size of the problem being solved. |
Preconditions:
Gc != NULL || Gh != NULL Gc != NULL && Gh != NULL] Gc->space_cols().is_compatible(Gh->space_cols()) == true Gc != NULL] Gc->space_cols().sub_space(var_dep()).get() != NULL Gc != NULL] Gc->space_cols().sub_space(var_indep()).get() != NULL Gc != NULL] Gc->space_rows().sub_space(equ_decomp()).get() != NULL Gc != NULL && equ_decomp().size() > 0 ] Gc.space_rows().sub_space(equ_decomp()).get() != NULL Gc != NULL && equ_undecomp().size() > 0 ] Gc.space_rows().sub_space(equ_undecomp()).get() != NULL C != NULL || D != NULL || GcUP != NULL Postconditions:
this->var_dep() != Range1D::Invalid && !this->var_dep().full_range() C != NULL && Gc != NULL && equ_decomp().size() > 0] C->space_cols().sub_space(equ_decomp())->is_compatible(Gc->space_rows().sub_space(equ_decomp())) && C->space_rows().is_compatible(Gc->space_cols().sub_space(var_dep())) C != NULL && Gh != NULL && inequ_decomp().size() > 0] C->space_cols().sub_space(equ_decomp().size()+inequ_decomp())->is_compatible(Gh->space_rows().sub_space(inequ_decomp())) && C->space_rows().is_compatible(Gh->space_cols().sub_space(var_dep())) D != NULL && Gc != NULL && var_indep().size() > 0 && equ_decomp().size() > 0] D->space_cols().sub_space(equ_decomp())->is_compatible(Gc->space_rows().sub_space(equ_decomp())) && D->space_rows().is_compatible(Gc->space_cols().sub_space(var_indep())) D != NULL && Gh != NULL && var_indep().size() > 0 && inequ_decomp().size() > 0] D->space_cols().sub_space(equ_decomp().size()+inequ_decomp())->is_compatible(Gh->space_rows().sub_space(inequ_decomp())) && D->space_rows().is_compatible(Gh->space_cols().sub_space(var_indep())) GcUP != NULL && var_indep().size() > 0 && equ_undecomp().size() > 0] GcUP->space_rows()->is_compatible(Gc->space_cols().sub_space(var_indep())) && GcUP->space_cols()->is_compatible(Gc->space_rows().sub_space(equ_undecomp())) This method with throw a SingularBasis exception if the updated basis matrix C is too close (as defined by the underlying implementation by some means) to being numerically singular.
Implemented in AbstractLinAlgPack::BasisSystemComposite, and AbstractLinAlgPack::BasisSystemPermDirectSparse.
 1.8.6
1.8.6