Implementation of the locally H(grad)-compatible FEM basis of variable order on the [-1,1] reference line cell, using Jacobi polynomials. More...
#include <Intrepid2_HGRAD_LINE_Cn_FEM_JACOBI.hpp>

Public Types | |
| typedef double | value_type |
| using | BasisBase = Basis< DeviceType, outputValueType, pointValueType > |
| using | ExecutionSpace = typename DeviceType::execution_space |
| (Kokkos) Execution space for basis. | |
| using | OrdinalTypeArray1DHost = Kokkos::View< ordinal_type *, typename ExecutionSpace::array_layout, Kokkos::HostSpace > |
| View type for 1d host array. | |
| using | OrdinalTypeArray2DHost = Kokkos::View< ordinal_type **, typename ExecutionSpace::array_layout, Kokkos::HostSpace > |
| View type for 2d host array. | |
| using | OrdinalTypeArray3DHost = Kokkos::View< ordinal_type ***, typename ExecutionSpace::array_layout, Kokkos::HostSpace > |
| View type for 3d host array. | |
| using | OutputViewType = Kokkos::DynRankView< OutputValueType, Kokkos::LayoutStride, DeviceType > |
| View type for basis value output. | |
| using | PointViewType = Kokkos::DynRankView< PointValueType, Kokkos::LayoutStride, DeviceType > |
| View type for input points. | |
| using | ScalarViewType = Kokkos::DynRankView< scalarType, Kokkos::LayoutStride, DeviceType > |
| View type for scalars. | |
 Public Types inherited from Intrepid2::Basis< DeviceType, outputValueType, pointValueType > Public Types inherited from Intrepid2::Basis< DeviceType, outputValueType, pointValueType > | |
| using | DeviceType = Device |
| (Kokkos) Device type on which Basis is templated. Does not necessarily return true for Kokkos::is_device (may be Kokkos::Serial, for example). | |
| using | ExecutionSpace = typename DeviceType::execution_space |
| (Kokkos) Execution space for basis. | |
| using | OutputValueType = outputValueType |
| Output value type for basis; default is double. | |
| using | PointValueType = pointValueType |
| Point value type for basis; default is double. | |
| using | OrdinalViewType = Kokkos::View< ordinal_type, DeviceType > |
| View type for ordinal. | |
| using | EBasisViewType = Kokkos::View< EBasis, DeviceType > |
| View for basis type. | |
| using | ECoordinatesViewType = Kokkos::View< ECoordinates, DeviceType > |
| View for coordinate system type. | |
| using | OrdinalTypeArray1DHost = Kokkos::View< ordinal_type *, typename ExecutionSpace::array_layout, Kokkos::HostSpace > |
| View type for 1d host array. | |
| using | OrdinalTypeArray2DHost = Kokkos::View< ordinal_type **, typename ExecutionSpace::array_layout, Kokkos::HostSpace > |
| View type for 2d host array. | |
| using | OrdinalTypeArray3DHost = Kokkos::View< ordinal_type ***, typename ExecutionSpace::array_layout, Kokkos::HostSpace > |
| View type for 3d host array. | |
| using | OrdinalTypeArrayStride1DHost = Kokkos::View< ordinal_type *, Kokkos::LayoutStride, Kokkos::HostSpace > |
| View type for 1d host array. | |
| using | OrdinalTypeArray1D = Kokkos::View< ordinal_type *, DeviceType > |
| View type for 1d device array. | |
| using | OrdinalTypeArray2D = Kokkos::View< ordinal_type **, DeviceType > |
| View type for 2d device array. | |
| using | OrdinalTypeArray3D = Kokkos::View< ordinal_type ***, DeviceType > |
| View type for 3d device array. | |
| using | OrdinalTypeArrayStride1D = Kokkos::View< ordinal_type *, Kokkos::LayoutStride, DeviceType > |
| View type for 1d device array. | |
|
typedef ScalarTraits < pointValueType > ::scalar_type | scalarType |
| Scalar type for point values. | |
| using | OutputViewType = Kokkos::DynRankView< OutputValueType, Kokkos::LayoutStride, DeviceType > |
| View type for basis value output. | |
| using | PointViewType = Kokkos::DynRankView< PointValueType, Kokkos::LayoutStride, DeviceType > |
| View type for input points. | |
| using | ScalarViewType = Kokkos::DynRankView< scalarType, Kokkos::LayoutStride, DeviceType > |
| View type for scalars. | |
Public Member Functions | |
| Basis_HGRAD_LINE_Cn_FEM_JACOBI (const ordinal_type order, const double alpha=0, const double beta=0) | |
| Constructor. | |
| virtual void | getValues (const ExecutionSpace &space, OutputViewType outputValues, const PointViewType inputPoints, const EOperator operatorType=OPERATOR_VALUE) const override |
| Evaluation of a FEM basis on a reference cell. More... | |
 Public Member Functions inherited from Intrepid2::Basis< DeviceType, outputValueType, pointValueType > Public Member Functions inherited from Intrepid2::Basis< DeviceType, outputValueType, pointValueType > | |
| OutputValueType | getDummyOutputValue () |
| Dummy array to receive input arguments. | |
| PointValueType | getDummyPointValue () |
| Dummy array to receive input arguments. | |
| Kokkos::DynRankView < OutputValueType, DeviceType > | allocateOutputView (const int numPoints, const EOperator operatorType=OPERATOR_VALUE) const |
| Allocate a View container suitable for passing to the getValues() variant that accepts Kokkos DynRankViews as arguments (as opposed to the Intrepid2 BasisValues and PointValues containers). More... | |
| virtual BasisValues < OutputValueType, DeviceType > | allocateBasisValues (TensorPoints< PointValueType, DeviceType > points, const EOperator operatorType=OPERATOR_VALUE) const |
| Allocate BasisValues container suitable for passing to the getValues() variant that takes a TensorPoints container as argument. More... | |
| virtual void | getScratchSpaceSize (ordinal_type &perTeamSpaceSize, ordinal_type &perThreadSpaceSize, const PointViewType inputPoints, const EOperator operatorType=OPERATOR_VALUE) const |
| Return the size of the scratch space, in bytes, needed for using the team-level implementation of getValues. More... | |
| virtual KOKKOS_INLINE_FUNCTION void | getValues (OutputViewType, const PointViewType, const EOperator, const typename Kokkos::TeamPolicy< ExecutionSpace >::member_type &teamMember, const typename ExecutionSpace::scratch_memory_space &scratchStorage, const ordinal_type subcellDim=-1, const ordinal_type subcellOrdinal=-1) const |
| Team-level evaluation of basis functions on a reference cell. More... | |
| virtual void | getValues (OutputViewType outputValues, const PointViewType inputPoints, const EOperator operatorType=OPERATOR_VALUE) const |
| virtual void | getValues (BasisValues< OutputValueType, DeviceType > outputValues, const TensorPoints< PointValueType, DeviceType > inputPoints, const EOperator operatorType=OPERATOR_VALUE) const |
| Evaluation of a FEM basis on a reference cell, using point and output value containers that allow preservation of tensor-product structure. More... | |
| virtual void | getValues (OutputViewType, const PointViewType, const PointViewType, const EOperator=OPERATOR_VALUE) const |
| Evaluation of an FVD basis evaluation on a physical cell. More... | |
| virtual void | getDofCoords (ScalarViewType) const |
| Returns spatial locations (coordinates) of degrees of freedom on the reference cell. | |
| virtual void | getDofCoeffs (ScalarViewType) const |
| Coefficients for computing degrees of freedom for Lagrangian basis If P is an element of the space spanned by the basis, := P(dofCoords(i)) dofCoeffs(i) are the nodal coefficients associated to basis function i. More... | |
| OrdinalTypeArray1DHost | getFieldOrdinalsForDegree (OrdinalTypeArray1DHost °rees) const |
| For hierarchical bases, returns the field ordinals that have at most the specified degree in each dimension. Assuming that these are less than or equal to the polynomial orders provided at Basis construction, the corresponding polynomials will form a superset of the Basis of the same type constructed with polynomial orders corresponding to the specified degrees. More... | |
| std::vector< int > | getFieldOrdinalsForDegree (std::vector< int > °rees) const |
| For hierarchical bases, returns the field ordinals that have at most the specified degree in each dimension. Assuming that these are less than or equal to the polynomial orders provided at Basis construction, the corresponding polynomials will form a superset of the Basis of the same type constructed with polynomial orders corresponding to the specified degrees. More... | |
| OrdinalTypeArray1DHost | getFieldOrdinalsForH1Degree (OrdinalTypeArray1DHost °rees) const |
| For hierarchical bases, returns the field ordinals that have at most the specified H^1 degree in each dimension. Assuming that these are less than or equal to the polynomial orders provided at Basis construction, the corresponding polynomials will form a superset of the Basis of the same type constructed with polynomial orders corresponding to the specified degrees. More... | |
| std::vector< int > | getFieldOrdinalsForH1Degree (std::vector< int > °rees) const |
| For hierarchical bases, returns the field ordinals that have at most the specified H^1 degree in each dimension. Assuming that these are less than or equal to the polynomial orders provided at Basis construction, the corresponding polynomials will form a superset of the Basis of the same type constructed with polynomial orders corresponding to the specified degrees. More... | |
| OrdinalTypeArray1DHost | getPolynomialDegreeOfField (int fieldOrdinal) const |
| For hierarchical bases, returns the polynomial degree (which may have multiple values in higher spatial dimensions) for the specified basis ordinal as a host array. More... | |
| OrdinalTypeArray1DHost | getH1PolynomialDegreeOfField (int fieldOrdinal) const |
| For hierarchical bases, returns the polynomial degree (which may have multiple values in higher spatial dimensions) for the specified basis ordinal as a host array. More... | |
| std::vector< int > | getPolynomialDegreeOfFieldAsVector (int fieldOrdinal) const |
| For hierarchical bases, returns the polynomial degree (which may have multiple values in higher spatial dimensions) for the specified basis ordinal as a host array. More... | |
| std::vector< int > | getH1PolynomialDegreeOfFieldAsVector (int fieldOrdinal) const |
| For hierarchical bases, returns the polynomial degree (which may have multiple values in higher spatial dimensions) for the specified basis ordinal as a host array. More... | |
| int | getPolynomialDegreeLength () const |
| For hierarchical bases, returns the number of entries required to specify the polynomial degree of a basis function. | |
| virtual const char * | getName () const |
| Returns basis name. More... | |
| virtual bool | requireOrientation () const |
| True if orientation is required. | |
| ordinal_type | getCardinality () const |
| Returns cardinality of the basis. More... | |
| ordinal_type | getDegree () const |
| Returns the degree of the basis. More... | |
| EFunctionSpace | getFunctionSpace () const |
| Returns the function space for the basis. More... | |
| shards::CellTopology | getBaseCellTopology () const |
| Returns the base cell topology for which the basis is defined. See Shards documentation https://trilinos.org/packages/shards for definition of base cell topology. More... | |
| EBasis | getBasisType () const |
| Returns the basis type. More... | |
| ECoordinates | getCoordinateSystem () const |
| Returns the type of coordinate system for which the basis is defined. More... | |
| ordinal_type | getDofCount (const ordinal_type subcDim, const ordinal_type subcOrd) const |
| DoF count for specified subcell. More... | |
| ordinal_type | getDofOrdinal (const ordinal_type subcDim, const ordinal_type subcOrd, const ordinal_type subcDofOrd) const |
| DoF tag to ordinal lookup. More... | |
| virtual int | getNumTensorialExtrusions () const |
| returns the number of tensorial extrusions relative to the cell topology returned by getBaseCellTopology(). Base class returns 0; overridden by TensorBasis. | |
| const OrdinalTypeArray3DHost | getAllDofOrdinal () const |
| DoF tag to ordinal data structure. | |
| const OrdinalTypeArrayStride1DHost | getDofTag (const ordinal_type dofOrd) const |
| DoF ordinal to DoF tag lookup. More... | |
| const OrdinalTypeArray2DHost | getAllDofTags () const |
| Retrieves all DoF tags. More... | |
| virtual BasisPtr< DeviceType, OutputValueType, PointValueType > | getSubCellRefBasis (const ordinal_type subCellDim, const ordinal_type subCellOrd) const |
| returns the basis associated to a subCell. More... | |
| ordinal_type | getDomainDimension () const |
| Returns the spatial dimension of the domain of the basis; this is equal to getBaseCellTopology().getDimension() + getNumTensorialExtrusions(). More... | |
| virtual HostBasisPtr < OutputValueType, PointValueType > | getHostBasis () const |
| Creates and returns a Basis object whose DeviceType template argument is Kokkos::HostSpace::device_type, but is otherwise identical to this. More... | |
Private Attributes | |
| double | alpha_ |
| double | beta_ |
Additional Inherited Members | |
 Protected Member Functions inherited from Intrepid2::Basis< DeviceType, outputValueType, pointValueType > Protected Member Functions inherited from Intrepid2::Basis< DeviceType, outputValueType, pointValueType > | |
| void | setOrdinalTagData (OrdinalTypeView3D &tagToOrdinal, OrdinalTypeView2D &ordinalToTag, const OrdinalTypeView1D tags, const ordinal_type basisCard, const ordinal_type tagSize, const ordinal_type posScDim, const ordinal_type posScOrd, const ordinal_type posDfOrd) |
| Fills ordinalToTag_ and tagToOrdinal_ by basis-specific tag data. More... | |
 Protected Attributes inherited from Intrepid2::Basis< DeviceType, outputValueType, pointValueType > Protected Attributes inherited from Intrepid2::Basis< DeviceType, outputValueType, pointValueType > | |
| ordinal_type | basisCardinality_ |
| Cardinality of the basis, i.e., the number of basis functions/degrees-of-freedom. | |
| ordinal_type | basisDegree_ |
| Degree of the largest complete polynomial space that can be represented by the basis. | |
| unsigned | basisCellTopologyKey_ |
| Identifier of the base topology of the cells for which the basis is defined. See the Shards package for definition of base cell topology. For TensorBasis subclasses, by default this the cell topology that is extruded (i.e., it is a lower-dimensional CellTopology than the space on which the tensor basis is defined). This allows tensor bases to be defined in higher dimensions than shards::CellTopology supports. TensorBasis subclasses can opt to use an equivalent shards CellTopology for base topology, as well as using Intrepid2's tagging for tensor bases in dimensions up to 3, by calling TensorBasis::setShardsTopologyAndTags(). | |
| EBasis | basisType_ |
| Type of the basis. | |
| ECoordinates | basisCoordinates_ |
| The coordinate system for which the basis is defined. | |
| EFunctionSpace | functionSpace_ |
| The function space in which the basis is defined. | |
| OrdinalTypeArray2DHost | ordinalToTag_ |
| "true" if tagToOrdinal_ and ordinalToTag_ have been initialized More... | |
| OrdinalTypeArray3DHost | tagToOrdinal_ |
| DoF tag to ordinal lookup table. More... | |
|
Kokkos::DynRankView < scalarType, DeviceType > | dofCoords_ |
| Coordinates of degrees-of-freedom for basis functions defined in physical space. | |
| Kokkos::DynRankView < scalarType, DeviceType > | dofCoeffs_ |
| Coefficients for computing degrees of freedom for Lagrangian basis If P is an element of the space spanned by the basis, := P(dofCoords_(i)) dofCoeffs_(i) are the nodal coefficients associated to basis functions i. More... | |
| OrdinalTypeArray2DHost | fieldOrdinalPolynomialDegree_ |
| Polynomial degree for each degree of freedom. Only defined for hierarchical bases right now. The number of entries per degree of freedom in this table depends on the basis type. For hypercubes, this will be the spatial dimension. We have not yet determined what this will be for simplices beyond 1D; there are not yet hierarchical simplicial bases beyond 1D in Intrepid2. More... | |
| OrdinalTypeArray2DHost | fieldOrdinalH1PolynomialDegree_ |
| H^1 polynomial degree for each degree of freedom. Only defined for hierarchical bases right now. The number of entries per degree of freedom in this table depends on the basis type. For hypercubes, this will be the spatial dimension. We have not yet determined what this will be for simplices beyond 1D; there are not yet hierarchical simplicial bases beyond 1D in Intrepid2. More... | |
Detailed Description
template<typename DeviceType = void, typename outputValueType = double, typename pointValueType = double>
class Intrepid2::Basis_HGRAD_LINE_Cn_FEM_JACOBI< DeviceType, outputValueType, pointValueType >
Implementation of the locally H(grad)-compatible FEM basis of variable order on the [-1,1] reference line cell, using Jacobi polynomials.
Implements Jacobi basis of variable order 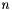 on the reference [-1,1] line cell. Jacobi polynomials depend on three parameters
on the reference [-1,1] line cell. Jacobi polynomials depend on three parameters 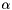 ,
, 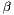 , and
, and 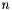 and are defined via the so-called Gamma function by
and are defined via the so-called Gamma function by
![\[ P_n^{(\alpha,\beta)} (z) = \frac{\Gamma (\alpha+n+1)}{n!\Gamma (\alpha+\beta+n+1)} \sum_{m=0}^n {n\choose m} \frac{\Gamma (\alpha + \beta + n + m + 1)}{\Gamma (\alpha + m + 1)} \left(\frac{z-1}{2}\right)^m \]](form_127.png)
The basis has cardinality 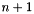 and spans a COMPLETE linear polynomial space. Basis functions are dual to a unisolvent set of degrees of freedom (DoF) enumerated as follows:
and spans a COMPLETE linear polynomial space. Basis functions are dual to a unisolvent set of degrees of freedom (DoF) enumerated as follows:
| Basis order | DoF tag table | DoF definition | |||
|---|---|---|---|---|---|
| subc dim | subc ordinal | subc DoF tag | subc num DoFs | ||
| 0 | 1 | 0 | 0 | 1 | 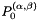 |
| 1 | 1 | 0 | 0-1 | 2 | 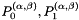 |
| 2 | 1 | 0 | 0-2 | 3 | 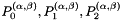 |
| 3 | 1 | 0 | 0-3 | 4 | 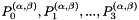 |
| ... | 1 | 0 | ... | ... | ... |
| n | 1 | 0 | 0-n | n+1 | 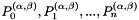 |
For example, for Legendre polynomials ( 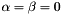 ), the first 11 bases are given by
), the first 11 bases are given by
| Basis order | DoF tag table | DoF definition | |||
|---|---|---|---|---|---|
| subc dim | subc ordinal | subc DoF tag | subc num DoFs | ||
| 0 | 1 | 0 | 0 | 1 | 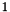 |
| 1 | 1 | 0 | 0-1 | 2 | and: 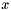 |
| 2 | 1 | 0 | 0-2 | 3 | and: 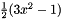 |
| 3 | 1 | 0 | 0-3 | 4 | and: 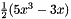 |
| 4 | 1 | 0 | 0-4 | 5 | and: 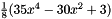 |
| 5 | 1 | 0 | 0-5 | 6 | and: 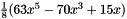 |
| 6 | 1 | 0 | 0-6 | 7 | and: 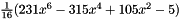 |
| 7 | 1 | 0 | 0-7 | 8 | and: 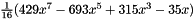 |
| 8 | 1 | 0 | 0-8 | 9 | and: 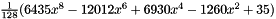 |
| 9 | 1 | 0 | 0-9 | 10 | and: 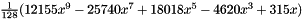 |
| 10 | 1 | 0 | 0-10 | 11 | and: 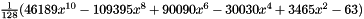 |
Definition at line 199 of file Intrepid2_HGRAD_LINE_Cn_FEM_JACOBI.hpp.
Member Function Documentation
|
inlineoverridevirtual |
Evaluation of a FEM basis on a reference cell.
Returns values of operatorType acting on FEM basis functions for a set of points in the reference cell for which the basis is defined.
- Parameters
-
space [in] - execution space instance outputValues [out] - variable rank array with the basis values inputPoints [in] - rank-2 array (P,D) with the evaluation points operatorType [in] - the operator acting on the basis functions
- Remarks
- For rank and dimension specifications of the output array see Section MD array template arguments for basis methods. Dimensions of ArrayScalar arguments are checked at runtime if HAVE_INTREPID2_DEBUG is defined.
- A FEM basis spans a COMPLETE or INCOMPLETE polynomial space on the reference cell which is a smooth function space. Thus, all operator types that are meaningful for the approximated function space are admissible. When the order of the operator exceeds the degree of the basis, the output array is filled with the appropriate number of zeros.
Reimplemented from Intrepid2::Basis< DeviceType, outputValueType, pointValueType >.
Definition at line 225 of file Intrepid2_HGRAD_LINE_Cn_FEM_JACOBI.hpp.
References Intrepid2::Basis< DeviceType, outputValueType, pointValueType >::getBaseCellTopology(), Intrepid2::Basis< DeviceType, outputValueType, pointValueType >::getCardinality(), and Intrepid2::Basis< DeviceType, outputValueType, pointValueType >::getDegree().
The documentation for this class was generated from the following files:
- http://docs.trilinos.org/dev/packages/intrepid2/src/Discretization/Basis/Intrepid2_HGRAD_LINE_Cn_FEM_JACOBI.hpp
- http://docs.trilinos.org/dev/packages/intrepid2/src/Discretization/Basis/Intrepid2_HGRAD_LINE_Cn_FEM_JACOBIDef.hpp
 1.8.5
1.8.5