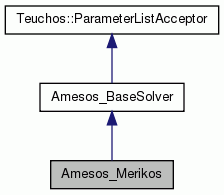
Amesos_Merikos: A parallel divide and conquer solver. More...

#include <Amesos_Merikos.h>

Inheritance diagram for Amesos_Merikos:

Collaboration diagram for Amesos_Merikos:

Public Member Functions

	Amesos_Merikos (const Epetra_LinearProblem &LinearProblem)
	Amesos_Merikos Constructor. More...

	~Amesos_Merikos (void)
	Amesos_Merikos Destructor. More...


int	RedistributeA ()
	Performs SymbolicFactorization on the matrix A. More...

int	ConvertToScalapack ()

int	PerformNumericFactorization ()

int	SymbolicFactorization ()
	Performs SymbolicFactorization on the matrix A. More...

int	NumericFactorization ()
	Performs NumericFactorization on the matrix A. More...

int	LSolve ()
	Solves L X = B. More...

int	USolve ()
	Solves U X = B. More...

int	Solve ()
	Solves A X = B. More...


const Epetra_LinearProblem *	GetProblem () const
	Get a pointer to the Problem.

bool	MatrixShapeOK () const
	Returns true if MERIKOS can handle this matrix shape. More...

int	SetUseTranspose (bool UseTranspose)
	SetUseTranpose() controls whether to compute AX=B or A^TX = B.

bool	UseTranspose () const
	Returns the current UseTranspose setting.

const Epetra_Comm &	Comm () const
	Returns a pointer to the Epetra_Comm communicator associated with this matrix.

int	SetParameters (Teuchos::ParameterList &ParameterList)
	Updates internal variables. More...

int	NumSymbolicFact () const
	Returns the number of symbolic factorizations performed by this object.

int	NumNumericFact () const
	Returns the number of numeric factorizations performed by this object.

int	NumSolve () const
	Returns the number of solves performed by this object.

void	PrintTiming ()
	Print timing information.

void	PrintStatus ()
	Print information about the factorization and solution phases.

Public Member Functions inherited from Amesos_BaseSolver
virtual	~Amesos_BaseSolver ()
	Destructor.

virtual void	PrintStatus () const =0
	Prints status information about the current solver.

virtual void	PrintTiming () const =0
	Prints timing information about the current solver.

virtual void	setParameterList (Teuchos::RCP< Teuchos::ParameterList > const &paramList)
	Redefined from Teuchos::ParameterListAcceptor (Does Not Work)

virtual Teuchos::RCP < Teuchos::ParameterList >	getNonconstParameterList ()
	This is an empty stub.

virtual Teuchos::RCP < Teuchos::ParameterList >	unsetParameterList ()
	This is an empty stub.

virtual void	GetTiming (Teuchos::ParameterList &TimingParameterList) const
	Extracts timing information from the current solver and places it in the parameter list. (Does Not Work)

Public Member Functions inherited from Teuchos::ParameterListAcceptor
virtual RCP< const ParameterList >	getParameterList () const

virtual RCP< const ParameterList >	getValidParameters () const

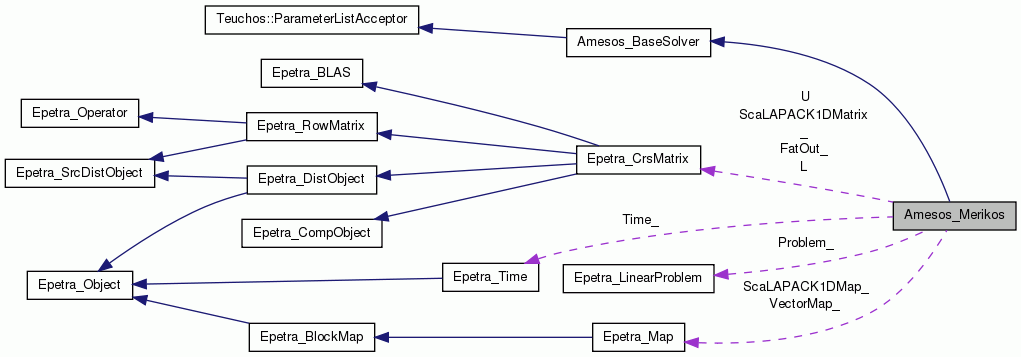
Protected Attributes
bool	UseTranspose_

const Epetra_LinearProblem *	Problem_

Epetra_CrsMatrix *	L

Epetra_CrsMatrix *	U

bool	PrintTiming_

bool	PrintStatus_

bool	ComputeVectorNorms_

bool	ComputeTrueResidual_

int	verbose_

int	debug_

double	ConTime_

double	SymTime_

double	NumTime_

double	SolTime_

double	VecTime_

double	MatTime_

int	NumSymbolicFact_

int	NumNumericFact_

int	NumSolve_

Epetra_Time *	Time_

Epetra_Map *	ScaLAPACK1DMap_

Epetra_CrsMatrix *	ScaLAPACK1DMatrix_

Epetra_Map *	VectorMap_

std::vector< double >	DenseA_

std::vector< int >	Ipiv_

int	NumOurRows_

int	NumOurColumns_

bool	TwoD_distribution_

int	grid_nb_

int	mypcol_

int	myprow_

Epetra_CrsMatrix *	FatOut_

int	nb_

int	lda_

int	iam_

int	nprow_

int	npcol_

int	NumGlobalElements_

int	m_per_p_

Detailed Description

Amesos_Merikos: A parallel divide and conquer solver.

Merikos partitions the rows of a matrix into two or more disjoint submatrices. i.e. if rows i and j are in different submatrices, A[i,j] == 0 == A[j,i]. Rows/columns not in any of the submatrices, i.e. the rows/columsn of the separator, are permuted to the bottom right.

Merikos factors each of the disjoint submatrices in parallel, (potentially by calling Amesos_Merikos() recursively), updating the rows and columns of the separator which belong to it and forming the schur complement of those rows and columns of the separator.

Merikos updates the trailing block of the matrix and then factors it.

Merikos is a Greek word for partial, reflecting the fact that Amesos_Merikos uses a series of partial LU factorizations, performed in parallel, to piece together the full LU decomposition.

Constructor & Destructor Documentation

Amesos_Merikos::Amesos_Merikos ( const Epetra_LinearProblem & LinearProblem )

Amesos_Merikos Constructor.

Creates an Amesos_Merikos instance, using an Epetra_LinearProblem, passing in an already-defined Epetra_LinearProblem object.

Amesos_Merikos::~Amesos_Merikos ( void )

Amesos_Merikos Destructor.

Completely deletes an Amesos_Merikos object.

Member Function Documentation

int Amesos_Merikos::LSolve ( )

Solves L X = B.

     | L11   0   0  |  X1      B1
     | L21 L22   0  |  X2   =  B2
     | L31 L32 L33  |  X3   =  B3

    Foreach subblock of the matrix do:
      Note:  this will happen in parallel
      Lsolve() 
        i.e. L11.Solve(X1, B1) and L22.Solve(X2, B2) 
      Update the elements of B corresponding to the seperator,
        i.e. B3 = B3 - L31 X1 - L32 X2 
    Endfor
    Perform a solve on the trailing matrix:
      i.e. L33.LSolve(X3,B3)

 \return Integer error code, set to 0 if successful.

bool Amesos_Merikos::MatrixShapeOK ( ) const

virtual

Returns true if MERIKOS can handle this matrix shape.

Returns true if the matrix shape is one that MERIKOS can handle. MERIKOS only works with square matrices.

Implements Amesos_BaseSolver.

int Amesos_Merikos::NumericFactorization ( )

virtual

Performs NumericFactorization on the matrix A.

    Static pivoting (i.e. scale and permute the matrix to
      produce a zero-free diagonal and to minimize the need for
      pivoting later).
    Partition the matrix 
    Redistribute the matrix to match the partitioning
    Foreach subblock of the matrix do:
      Note:  this will happen in parallel
      Create an instance of an Amesos solver object (must  
        support the Amesos_Component interface)
      Call PartialFactorization 
      Add the Schur Complement into the trailing block of the matrix.
    Endfor
    Create an Amesos instance for the trailing block of the matrix.
    Call SymbolicFactorization on the trailing block 
    Call NumericFactorization on the trailing block

 \return Integer error code, set to 0 if successful.

Implements Amesos_BaseSolver.

int Amesos_Merikos::RedistributeA ( )

Performs SymbolicFactorization on the matrix A.

SymbolicFactorization() takes no action in Amesos_Merikos().

Returns: Integer error code, set to 0 if successful.

int Amesos_Merikos::SetParameters ( Teuchos::ParameterList & ParameterList )

virtual

Updates internal variables.

Returns: Integer error code, set to 0 if successful.

Implements Amesos_BaseSolver.

int Amesos_Merikos::Solve ( )

virtual

Solves A X = B.

     | L11     U12     U13  |  X1      B1
     | L21     L22     U23  |  X2   =  B2
     | L31     L32         A33  |  X3   =  B3

    Foreach subblock of the matrix do:
      Note:  this will happen in parallel
      Lsolve() 
        i.e. L11.Solve(X1, B1) and L22.Solve(X2, B2) 
      Update the elements of B corresponding to the seperator,
        i.e. B3 = B3 - L31 X1 - L32 X2 
    Endfor
    Perform a solve on the trailing matrix:
      i.e. A33.Solve(X3,B3)

    B = X ;
    Foreach subblock of the matrix do:
      Note:  this will happen in parallel
      Update the elements of B corresponding to this block
        i.e. B2 = B2 - U23 X3 ; B1 = B1 - U13 X3 
      Usolve() 
        i.e. U11.Solve(X1, B1) and U22.Solve(X2, B2) 
    Endfor

 \return Integer error code, set to 0 if successful.

Implements Amesos_BaseSolver.

int Amesos_Merikos::SymbolicFactorization ( )

virtual

Performs SymbolicFactorization on the matrix A.

In addition to performing symbolic factorization on the matrix A, the call to SymbolicFactorization() implies that no change will be made to the non-zero structure of the underlying matrix without a subsequent call to SymbolicFactorization().

<br >Preconditions:

GetProblem().GetOperator() != 0 (return -1)
MatrixShapeOk(GetProblem().GetOperator()) == true (return -6)

<br >Postconditions:

Symbolic Factorization will be performed (or marked to be performed) allowing NumericFactorization() and Solve() to be called.

Returns: Integer error code, set to 0 if successful.

Implements Amesos_BaseSolver.

int Amesos_Merikos::USolve ( )

Solves U X = B.

     | U11 U12 U13  |  X1      B1
     |   0 U22 U23  |  X2   =  B2
     |   0   0 U33  |  X3   =  B3

    Perform a solve on the trailing matrix:
      i.e. U33.USolve(X3,B3) 
    Foreach subblock of the matrix do:
      Note:  this will happen in parallel
      Update the elements of B corresponding to this block
        i.e. B2 = B2 - U23 X3 ; B1 = B1 - U13 X3 
      Usolve() 
        i.e. U11.Solve(X1, B1) and U22.Solve(X2, B2) 
    Endfor

 \return Integer error code, set to 0 if successful.

The documentation for this class was generated from the following file:

Amesos_Merikos.h

Public Member Functions

Protected Attributes

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation