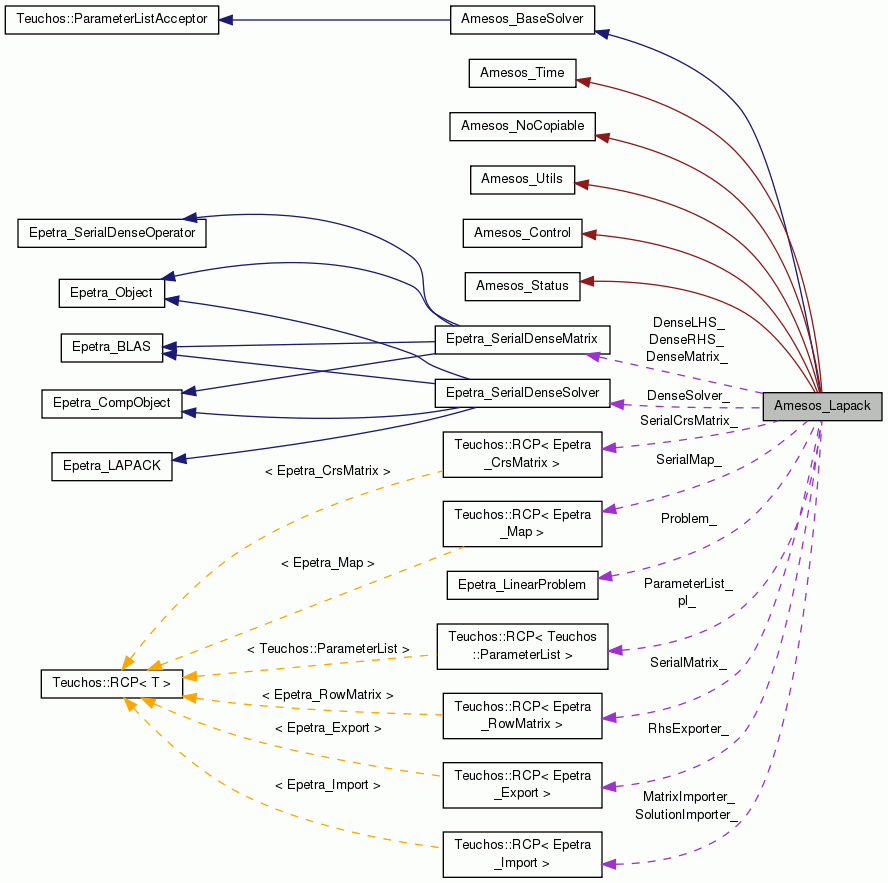
Amesos_Lapack: an interface to LAPACK. More...

#include <Amesos_Lapack.h>

Inheritance diagram for Amesos_Lapack:

Collaboration diagram for Amesos_Lapack:

Public Member Functions

	Amesos_Lapack (const Epetra_LinearProblem &LinearProblem)
	Amesos_Lapack Constructor. More...

	~Amesos_Lapack (void)
	Amesos_Lapack Destructor. More...


int	SymbolicFactorization ()
	Performs SymbolicFactorization on the matrix A. More...

int	NumericFactorization ()
	Performs NumericFactorization on the matrix A. More...

int	Solve ()
	Solves A X = B (or A^T x = B) More...


const Epetra_LinearProblem *	GetProblem () const
	Returns the Epetra_LinearProblem. More...

bool	MatrixShapeOK () const
	Returns true if the solver can handle this matrix shape. More...

int	SetUseTranspose (bool UseTranspose_in)
	If set true, X will be set to the solution of A^T X = B (not A X = B) More...

bool	UseTranspose () const
	Returns the current UseTranspose setting.

const Epetra_Comm &	Comm () const
	Returns a pointer to the Epetra_Comm communicator associated with this operator.

void	setParameterList (Teuchos::RCP< Teuchos::ParameterList > const &paramList)
	Use this parameter list to read values from. More...

Teuchos::RCP < Teuchos::ParameterList >	unsetParameterList ()
	This is an empty stub.

int	SetParameters (Teuchos::ParameterList &ParameterList)
	Deprecated - Sets parameters.

int	GEEV (Epetra_Vector &Er, Epetra_Vector &Ei)
	Computes the eigenvalues of the linear system matrix using DGEEV. More...

int	NumSymbolicFact () const
	Returns the number of symbolic factorizations performed by this object.

int	NumNumericFact () const
	Returns the number of numeric factorizations performed by this object.

int	NumSolve () const
	Returns the number of solves performed by this object.

void	PrintTiming () const
	Print timing information.

void	PrintStatus () const
	Print information about the factorization and solution phases.

void	GetTiming (Teuchos::ParameterList &TimingParameterList) const
	Extracts timing information from the current solver and places it in the parameter list.

Public Member Functions inherited from Amesos_BaseSolver
virtual	~Amesos_BaseSolver ()
	Destructor.

virtual Teuchos::RCP < Teuchos::ParameterList >	getNonconstParameterList ()
	This is an empty stub.

Public Member Functions inherited from Teuchos::ParameterListAcceptor
virtual RCP< const ParameterList >	getParameterList () const

virtual RCP< const ParameterList >	getValidParameters () const

Protected Member Functions
const Epetra_RowMatrix *	Matrix () const
	Returns a pointer to the linear system matrix.

int	NumGlobalRows () const
	Returns the number of global rows, or -1 if Matrix() returns 0.

long long	NumGlobalRows64 () const

int	NumMyRows () const
	Returns the number of local rows, or -1 if Matrix() returns 0.

const Epetra_Map &	SerialMap ()
	Returns a reference to serial map (that with all elements on process 0).

Epetra_RowMatrix &	SerialMatrix ()
	Returns a reference to serial matrix (that with all rows on process 0).

Epetra_CrsMatrix &	SerialCrsMatrix ()

const Epetra_Import &	MatrixImporter ()
	Returns a reference to the matrix importer (from row map to serial map).

const Epetra_Export &	RhsExporter ()
	Returns a reference to the rhs exporter (from range map to serial map).

const Epetra_Import &	SolutionImporter ()
	Returns a reference to the solution importer (to domain map from serial map).

int	SolveSerial (Epetra_MultiVector &X, const Epetra_MultiVector &B)
	Solves the linear system, when only one process is used.

int	SolveDistributed (Epetra_MultiVector &X, const Epetra_MultiVector &B)
	Solves the linear system, when more than one process is used.

int	DistributedToSerial ()
	Converts a distributed matrix to serial matrix.

int	SerialToDense ()
	Converts a serial matrix to dense format.

int	DenseToFactored ()
	Factors the matrix using LAPACK.

Protected Attributes
Teuchos::RCP < Teuchos::ParameterList >	pl_

Teuchos::RCP< Epetra_RowMatrix >	SerialMatrix_

Teuchos::RCP< Epetra_CrsMatrix >	SerialCrsMatrix_

Teuchos::RCP< Epetra_Map >	SerialMap_

Teuchos::RCP< Epetra_Import >	MatrixImporter_

Teuchos::RCP< Epetra_Export >	RhsExporter_

Teuchos::RCP< Epetra_Import >	SolutionImporter_

Epetra_SerialDenseMatrix	DenseMatrix_
	Dense matrix.

Epetra_SerialDenseMatrix	DenseLHS_
	Dense LHS.

Epetra_SerialDenseMatrix	DenseRHS_
	Dense RHS.

Epetra_SerialDenseSolver	DenseSolver_
	Linear problem for dense matrix and vectors.

bool	UseTranspose_
	If `true`, the linear system with the transpose will be solved.

const Epetra_LinearProblem *	Problem_
	Pointer to the linear problem.

int	MtxRedistTime_
	Quick access ids for the individual timings.

int	MtxConvTime_

int	VecRedistTime_

int	SymFactTime_

int	NumFactTime_

int	SolveTime_

long long	NumGlobalRows_

long long	NumGlobalNonzeros_

Teuchos::RCP < Teuchos::ParameterList >	ParameterList_

Detailed Description

Amesos_Lapack: an interface to LAPACK.

Class Amesos_Lapack enables the solution of the distributed linear system, defined by an Epetra_LinearProblem, using LAPACK.

Amesos_Lapack stores the lineaar system matrix as an Epetra_SerialDensMatrix. The linear problem is an Epetra_SerialDenseProblem. Amesos_Lapack factorizes the matrix using DGETRF().

Date: Last updated on 16-Mar-05.

Author: Marzio Sala, 9214.

Constructor & Destructor Documentation

Amesos_Lapack::Amesos_Lapack ( const Epetra_LinearProblem & LinearProblem )

Amesos_Lapack Constructor.

Creates an Amesos_Lapack instance, using an Epetra_LinearProblem, passing in an already-defined Epetra_LinearProblem object.

Note: The operator in LinearProblem must be an Epetra_RowMatrix.

References unsetParameterList().

Amesos_Lapack::~Amesos_Lapack ( void )

Amesos_Lapack Destructor.

Completely deletes an Amesos_Lapack object.

References PrintStatus(), Amesos_Status::PrintStatus_, PrintTiming(), Amesos_Status::PrintTiming_, and Amesos_Status::verbose_.

Member Function Documentation

int Amesos_Lapack::GEEV	(	Epetra_Vector &	Er,
		Epetra_Vector &	Ei
	)

Computes the eigenvalues of the linear system matrix using DGEEV.

Parameters

Er	- (Out) On processor zero only, it will contain the real component of the eigenvalues.
Ei	- (Out) On processor zero only, it will contain the imaginary component of the eigenvalues.

Note: Er and Ei must have been allocated so that the local length on processor 0 equals the global size of the matrix.

References Epetra_SerialDenseMatrix::A(), DenseMatrix_, DistributedToSerial(), Epetra_LAPACK::GEEV(), Insert, Amesos_Status::IsSymbolicFactorizationOK_, Teuchos::rcp(), SerialMap(), SerialToDense(), Epetra_SerialDenseMatrix::Shape(), and SymbolicFactorization().

const Epetra_LinearProblem* Amesos_Lapack::GetProblem ( ) const

inlinevirtual

Returns the Epetra_LinearProblem.

Warning! Do not call return->SetOperator(...) to attempt to change the Epetra_Operator object (even if the new matrix has the same structure). This new operator matrix will be ignored!

Implements Amesos_BaseSolver.

References Problem_.

Referenced by Comm(), MatrixShapeOK(), and SymbolicFactorization().

bool Amesos_Lapack::MatrixShapeOK ( ) const

virtual

Returns true if the solver can handle this matrix shape.

Returns true if the matrix shape is one that the underlying sparse direct solver can handle. Classes that work only on square matrices should return false for rectangular matrices. Classes that work only on symmetric matrices whould return false for non-symmetric matrices.

Implements Amesos_BaseSolver.

References GetProblem().

int Amesos_Lapack::NumericFactorization ( )

virtual

Performs NumericFactorization on the matrix A.

In addition to performing numeric factorization on the matrix A, the call to NumericFactorization() implies that no change will be made to the underlying matrix without a subsequent call to NumericFactorization().

Preconditions:

GetProblem().GetOperator() != 0 (return -1)
MatrixShapeOk(GetProblem().GetOperator()) == true (return -6)
The non-zero structure of the matrix should not have changed since the last call to SymbolicFactorization(). (return -2 if the number of non-zeros changes) Other changes can have arbitrary consequences.
The distribution of the matrix should not have changed since the last call to SymbolicFactorization()
The matrix should be indexed from 0 to n-1, unless the parameter "Reindex" was set to "true" prior to the call to SymbolicFactorization(). (return -3 - if caught)
The paremeter "Reindex" should not be set to "true" except on CrsMatrices. (return -4)
The paremeter "Reindex" should not be set to "true" unless Amesos was built with EpetraExt, i.e. with –enable-epetraext on the configure line. (return -4)
Internal errors retur -5.

Postconditions:

Numeric Factorization will be performed (or marked to be performed) allowing Solve() to be performed correctly despite a potential change in in the matrix values (though not in the non-zero structure).

Returns: Integer error code, set to 0 if successful.

Implements Amesos_BaseSolver.

References DenseMatrix_, DenseToFactored(), DistributedToSerial(), Amesos_Status::IsNumericFactorizationOK_, Amesos_Status::IsSymbolicFactorizationOK_, Amesos_Status::NumNumericFact_, SerialToDense(), Epetra_SerialDenseMatrix::Shape(), and SymbolicFactorization().

Referenced by Solve().

void Amesos_Lapack::setParameterList ( Teuchos::RCP< Teuchos::ParameterList > const & paramList )

virtual

Use this parameter list to read values from.

Redefined from Teuchos::ParameterListAcceptor

Reimplemented from Amesos_BaseSolver.

References Amesos_Control::AddToDiag_, Amesos_Control::AddZeroToDiag_, DenseSolver_, Epetra_SerialDenseSolver::FactorWithEquilibration(), Teuchos::ParameterList::get(), and Teuchos::ParameterList::sublist().

Referenced by unsetParameterList().

int Amesos_Lapack::SetUseTranspose ( bool UseTranspose )

inlinevirtual

If set true, X will be set to the solution of A^T X = B (not A X = B)

If the implementation of this interface does not support transpose use, this method should return a value of -1.

Preconditions:

SetUseTranspose() should be called prior to the call to SymbolicFactorization() If NumericFactorization() or Solve() is called after SetUseTranspose() without an intervening call to SymbolicFactorization() the result is implementation dependent.

Postconditions:

The next factorization and solve will be performed with the new value of UseTranspose.

Parameters

UseTranspose – (In) If true, solve A^T X = B, otherwise solve A X = B.

Returns: Integer error code, set to 0 if successful. Set to -1 if this implementation does not support transpose.

Implements Amesos_BaseSolver.

References UseTranspose_.

int Amesos_Lapack::Solve ( )

virtual

Solves A X = B (or A^T x = B)

Preconditions:

GetProblem().GetOperator() != 0 (return -1)
MatrixShapeOk(GetProblem().GetOperator()) == true (return -6)
GetProblem()->CheckInput (see Epetra_LinearProblem::CheckInput() for return values)
The non-zero structure of the matrix should not have changed since the last call to SymbolicFactorization().
The distribution of the matrix should not have changed since the last call to SymbolicFactorization()
The matrix should not have changed since the last call to NumericFactorization().

Postconditions:

X will be set such that A X = B (or A^T X = B), within the limits of the accuracy of the underlying solver.

Returns: Integer error code, set to 0 if successful.

Implements Amesos_BaseSolver.

References Epetra_LinearProblem::GetLHS(), Epetra_LinearProblem::GetRHS(), Amesos_Status::IsNumericFactorizationOK_, NumericFactorization(), Problem_, SolveDistributed(), and SolveSerial().

int Amesos_Lapack::SymbolicFactorization ( )

virtual

Performs SymbolicFactorization on the matrix A.

In addition to performing symbolic factorization on the matrix A, the call to SymbolicFactorization() implies that no change will be made to the non-zero structure of the underlying matrix without a subsequent call to SymbolicFactorization().

Preconditions:

GetProblem().GetOperator() != 0 (return -1)
MatrixShapeOk(GetProblem().GetOperator()) == true (return -6)

Postconditions:

Symbolic Factorization will be performed (or marked to be performed) allowing NumericFactorization() and Solve() to be called.

Returns: Integer error code, set to 0 if successful.

Implements Amesos_BaseSolver.

References Amesos_Time::AddTime(), Comm(), Amesos_Time::CreateTimer(), Teuchos::RCP< T >::get(), GetProblem(), Amesos_Status::IsNumericFactorizationOK_, Amesos_Status::IsSymbolicFactorizationOK_, Matrix(), Epetra_Comm::MyPID(), Epetra_Comm::NumProc(), Amesos_Status::NumSymbolicFact_, Epetra_Operator::OperatorDomainMap(), Epetra_Operator::OperatorRangeMap(), rcp(), Amesos_Time::ResetTimer(), SerialMap(), Epetra_Operator::UseTranspose(), and UseTranspose_.

Referenced by GEEV(), and NumericFactorization().

The documentation for this class was generated from the following files:

Amesos_Lapack.h
Amesos_Lapack.cpp

Public Member Functions

Protected Member Functions

Protected Attributes

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation