|
Tempus
Version of the Day
Time Integration
|
|
Tempus
Version of the Day
Time Integration
|
Thyra Base interface for implicit time steppers. More...
#include <Tempus_StepperImplicit_decl.hpp>

Public Member Functions | |
| virtual bool | isValidSetup (Teuchos::FancyOStream &out) const |
Basic implicit stepper methods | |
| virtual void | setModel (const Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > &appModel) |
| virtual Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > | getModel () |
| virtual Teuchos::RCP< const WrapperModelEvaluator< Scalar > > | getWrapperModel () |
| virtual void | setDefaultSolver () |
| virtual void | setSolver (Teuchos::RCP< Thyra::NonlinearSolverBase< Scalar > > solver) |
| Set solver. More... | |
| virtual Teuchos::RCP < Thyra::NonlinearSolverBase < Scalar > > | getSolver () const |
| Get solver. More... | |
| virtual void | setInitialConditions (const Teuchos::RCP< SolutionHistory< Scalar > > &solutionHistory) |
| Set the initial conditions and make them consistent. More... | |
| virtual Scalar | getAlpha (const Scalar dt) const =0 |
| Return alpha = d(xDot)/dx. More... | |
| virtual Scalar | getBeta (const Scalar dt) const =0 |
| Return beta = d(x)/dx. More... | |
| const Thyra::SolveStatus< Scalar > | solveImplicitODE (const Teuchos::RCP< Thyra::VectorBase< Scalar > > &x) |
| Solve problem using x in-place. (Needs to be deprecated!) More... | |
| const Thyra::SolveStatus< Scalar > | solveImplicitODE (const Teuchos::RCP< Thyra::VectorBase< Scalar > > &x, const Teuchos::RCP< Thyra::VectorBase< Scalar > > &xDot, const Scalar time, const Teuchos::RCP< ImplicitODEParameters< Scalar > > &p) |
| Solve implicit ODE, f(x, xDot, t, p) = 0. More... | |
| void | evaluateImplicitODE (Teuchos::RCP< Thyra::VectorBase< Scalar > > &f, const Teuchos::RCP< Thyra::VectorBase< Scalar > > &x, const Teuchos::RCP< Thyra::VectorBase< Scalar > > &xDot, const Scalar time, const Teuchos::RCP< ImplicitODEParameters< Scalar > > &p) |
| Evaluate implicit ODE residual, f(x, xDot, t, p). More... | |
| virtual void | setInitialGuess (Teuchos::RCP< const Thyra::VectorBase< Scalar > > initialGuess) |
| Pass initial guess to Newton solver (only relevant for implicit solvers) More... | |
| virtual void | setZeroInitialGuess (bool zIG) |
| Set parameter so that the initial guess is set to zero (=True) or use last timestep (=False). More... | |
| virtual bool | getZeroInitialGuess () const |
| virtual Scalar | getInitTimeStep (const Teuchos::RCP< SolutionHistory< Scalar > > &) const |
Overridden from Teuchos::Describable | |
| virtual void | describe (Teuchos::FancyOStream &out, const Teuchos::EVerbosityLevel verbLevel) const |
 Public Member Functions inherited from Tempus::Stepper< Scalar > Public Member Functions inherited from Tempus::Stepper< Scalar > | |
| virtual Teuchos::RCP< const Teuchos::ParameterList > | getValidParameters () const =0 |
| virtual void | setNonConstModel (const Teuchos::RCP< Thyra::ModelEvaluator< Scalar > > &) |
| virtual void | setObserver (Teuchos::RCP< StepperObserver< Scalar > > obs=Teuchos::null) |
| Set Observer. More... | |
| virtual Teuchos::RCP < StepperObserver< Scalar > > | getObserver () const |
| Get Observer. More... | |
| virtual void | initialize () |
| Initialize after construction and changing input parameters. More... | |
| virtual bool | isInitialized () |
| True if stepper's member data is initialized. More... | |
| virtual void | checkInitialized () |
| Check initialization, and error out on failure. More... | |
| virtual void | takeStep (const Teuchos::RCP< SolutionHistory< Scalar > > &solutionHistory)=0 |
| Take the specified timestep, dt, and return true if successful. More... | |
| virtual Teuchos::RCP < Tempus::StepperState< Scalar > > | getDefaultStepperState ()=0 |
| virtual Scalar | getOrder () const =0 |
| virtual Scalar | getOrderMin () const =0 |
| virtual Scalar | getOrderMax () const =0 |
| virtual bool | isExplicit () const =0 |
| virtual bool | isImplicit () const =0 |
| virtual bool | isExplicitImplicit () const =0 |
| virtual bool | isOneStepMethod () const =0 |
| virtual bool | isMultiStepMethod () const =0 |
| void | setStepperType (std::string s) |
| std::string | getStepperType () const |
| void | setUseFSAL (bool a) |
| bool | getUseFSAL () const |
| virtual bool | getUseFSALDefault () const |
| void | setICConsistency (std::string s) |
| std::string | getICConsistency () const |
| virtual std::string | getICConsistencyDefault () const |
| void | setICConsistencyCheck (bool c) |
| bool | getICConsistencyCheck () const |
| virtual bool | getICConsistencyCheckDefault () const |
| virtual OrderODE | getOrderODE () const =0 |
| virtual Teuchos::RCP < Thyra::VectorBase< Scalar > > | getStepperX (Teuchos::RCP< SolutionState< Scalar > > state) |
| Get x from SolutionState or Stepper storage. More... | |
| virtual Teuchos::RCP < Thyra::VectorBase< Scalar > > | getStepperXDot (Teuchos::RCP< SolutionState< Scalar > > state) |
| Get xDot from SolutionState or Stepper storage. More... | |
| virtual Teuchos::RCP < Thyra::VectorBase< Scalar > > | getStepperXDotDot (Teuchos::RCP< SolutionState< Scalar > > state) |
| Get xDotDot from SolutionState or Stepper storage. More... | |
| virtual std::string | description () const |
| virtual void | createSubSteppers (std::vector< Teuchos::RCP< const Thyra::ModelEvaluator< Scalar > > >) |
Protected Attributes | |
| Teuchos::RCP < WrapperModelEvaluator < Scalar > > | wrapperModel_ |
| Teuchos::RCP < Thyra::NonlinearSolverBase < Scalar > > | solver_ |
| Teuchos::RCP< const Thyra::VectorBase< Scalar > > | initialGuess_ |
| bool | zeroInitialGuess_ |
| Teuchos::RCP< StepperObserver < Scalar > > | stepperObserver_ |
 Protected Attributes inherited from Tempus::Stepper< Scalar > Protected Attributes inherited from Tempus::Stepper< Scalar > | |
| bool | isInitialized_ = false |
| True if stepper's member data is initialized. More... | |
Additional Inherited Members | |
 Protected Member Functions inherited from Tempus::Stepper< Scalar > Protected Member Functions inherited from Tempus::Stepper< Scalar > | |
| virtual void | setStepperX (Teuchos::RCP< Thyra::VectorBase< Scalar > > x) |
| Set x for Stepper storage. More... | |
| virtual void | setStepperXDot (Teuchos::RCP< Thyra::VectorBase< Scalar > > xDot) |
| Set xDot for Stepper storage. More... | |
| virtual void | setStepperXDotDot (Teuchos::RCP< Thyra::VectorBase< Scalar > > xDotDot) |
| Set x for Stepper storage. More... | |
Thyra Base interface for implicit time steppers.
For first-order ODEs, we can write the implicit ODE as
![\[ \mathcal{F}(\dot{x}_n,x_n,t_n) = 0 \]](form_193.png)
where 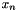 is the solution vector,
is the solution vector, 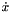 is the time derivative,
is the time derivative,  is the time and
is the time and  indicates the
indicates the  time level. Note that
time level. Note that  is different for each time stepper and is a function of other solution states, e.g., for Backward Euler,
is different for each time stepper and is a function of other solution states, e.g., for Backward Euler,
![\[ \dot{x}_n(x_n) = \frac{x_n - x_{n-1}}{\Delta t} \]](form_197.png)
Defining the Iteration Matrix
Often we use Newton's method or one of its variations to solve for 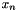 , such as
, such as
![\[ \left[ \frac{\partial}{\partial x_n} \left( \mathcal{F}(\dot{x}_n,x_n,t_n) \right) \right] \Delta x_n^\nu = - \mathcal{F}(\dot{x}_n^\nu,x_n^\nu,t_n) \]](form_198.png)
where  and
and  is the iteration index. Using the chain rule for a function with multiple variables, we can write
is the iteration index. Using the chain rule for a function with multiple variables, we can write
![\[ \left[ \frac{\partial \dot{x}_n(x_n) }{\partial x_n} \frac{\partial}{\partial \dot{x}_n} \left( \mathcal{F}(\dot{x}_n,x_n,t_n) \right) + \frac{\partial x_n}{\partial x_n} \frac{\partial}{\partial x_n} \left( \mathcal{F}(\dot{x}_n,x_n,t_n) \right) \right] \Delta x_n^\nu = - \mathcal{F}(\dot{x}_n^\nu,x_n^\nu,t_n) \]](form_201.png)
Defining the iteration matrix, 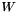 , we have
, we have
![\[ W \Delta x_n^\nu = - \mathcal{F}(\dot{x}_n^\nu,x_n^\nu,t_n) \]](form_202.png)
using  , where
, where
![\[ W = \alpha \frac{\partial \mathcal{F}_n}{\partial \dot{x}_n} + \beta \frac{\partial \mathcal{F}_n}{\partial x_n} \]](form_204.png)
and
![\[ W = \alpha M + \beta J \]](form_205.png)
where
![\[ \alpha \equiv \frac{\partial \dot{x}_n(x_n) }{\partial x_n}, \quad \quad \beta \equiv \frac{\partial x_n}{\partial x_n} = 1, \quad \quad M = \frac{\partial \mathcal{F}_n}{\partial \dot{x}_n}, \quad \quad J = \frac{\partial \mathcal{F}_n}{\partial x_n} \]](form_206.png)
and  is the mass matrix and
is the mass matrix and  is the Jacobian.
is the Jacobian.
Note that sometimes it is helpful to set  and
and  to obtain the Jacobian,
to obtain the Jacobian,  , from the iteration matrix (i.e., ModelEvaluator), or set
, from the iteration matrix (i.e., ModelEvaluator), or set  and
and 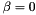 to obtain the mass matrix,
to obtain the mass matrix,  , from the iteration matrix (i.e., the ModelEvaluator).
, from the iteration matrix (i.e., the ModelEvaluator).
As a concrete example, the time derivative for Backward Euler is
![\[ \dot{x}_n(x_n) = \frac{x_n - x_{n-1}}{\Delta t} \]](form_197.png)
thus
![\[ \alpha \equiv \frac{\partial \dot{x}_n(x_n) }{\partial x_n} = \frac{1}{\Delta t} \quad \quad \beta \equiv \frac{\partial x_n}{\partial x_n} = 1 \]](form_212.png)
and the iteration matrix for Backward Euler is
![\[ W = \frac{1}{\Delta t} \frac{\partial \mathcal{F}_n}{\partial \dot{x}_n} + \frac{\partial \mathcal{F}_n}{\partial x_n} \]](form_213.png)
Dangers of multiplying through by  . In some time-integration schemes, the application might want to multiply the governing equations by the time-step size,
. In some time-integration schemes, the application might want to multiply the governing equations by the time-step size,  , for scaling or other reasons. Here we illustrate what that means and the complications that follow from it.
, for scaling or other reasons. Here we illustrate what that means and the complications that follow from it.
Starting with a simple implicit ODE and multiplying through by  , we have
, we have
![\[ \mathcal{F}_n = \Delta t \dot{x}_n - \Delta t \bar{f}(x_n,t_n) = 0 \]](form_214.png)
For the Backward Euler stepper, we recall from above that
![\[ \dot{x}_n(x_n) = \frac{x_n - x_{n-1}}{\Delta t} \quad\quad \alpha \equiv \frac{\partial \dot{x}_n(x_n) }{\partial x_n} = \frac{1}{\Delta t} \quad \quad \beta \equiv \frac{\partial x_n}{\partial x_n} = 1 \]](form_215.png)
and we can find for our simple implicit ODE,  ,
,
![\[ M = \frac{\partial \mathcal{F}_n}{\partial \dot{x}_n} = \Delta t, \quad \quad J = \frac{\partial \mathcal{F}_n}{\partial x_n} = -\Delta t \frac{\partial \bar{f}_n}{\partial x_n} \]](form_217.png)
Thus this iteration matrix,  , is
, is
![\[ W^\ast = \alpha \frac{\partial \mathcal{F}_n}{\partial \dot{x}_n} + \beta \frac{\partial \mathcal{F}_n}{\partial x_n} = \frac{1}{\Delta t} \Delta t + (1) \left( - \Delta t \frac{\partial \bar{f}_n}{\partial x_n} \right) \]](form_219.png)
or simply
![\[ W^\ast = 1 - \Delta t \frac{\partial \bar{f}_n}{\partial x_n} \]](form_220.png)
Note that  is not the same as
is not the same as 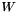 from above (i.e.,
from above (i.e.,  ). But we should not infer from this is that
). But we should not infer from this is that  or
or  , as those definitions are unchanged (i.e.,
, as those definitions are unchanged (i.e.,  and
and  ). However, the mass matrix,
). However, the mass matrix,  , the Jacobian,
, the Jacobian,  and the residual,
and the residual,  , all need to include
, all need to include  in their evaluations (i.e., be included in the ModelEvaluator return values for these terms).
in their evaluations (i.e., be included in the ModelEvaluator return values for these terms).
Dangers of explicitly including time-derivative definition. If we explicitly include the time-derivative defintion for Backward Euler, we find for our simple implicit ODE,
![\[ \mathcal{F}_n = \frac{x_n - x_{n-1}}{\Delta t} - \bar{f}(x_n,t_n) = 0 \]](form_227.png)
that the iteration matrix is
![\[ W^{\ast\ast} = \alpha \frac{\partial \mathcal{F}_n}{\partial \dot{x}_n} + \beta \frac{\partial \mathcal{F}_n}{\partial x_n} = \frac{1}{\Delta t} (0) + (1) \left(\frac{1}{\Delta t} - \frac{\partial \bar{f}_n}{\partial x_n} \right) \]](form_228.png)
or simply
![\[ W^{\ast\ast} = \frac{1}{\Delta t} - \frac{\partial \bar{f}_n}{\partial x_n} \]](form_229.png)
which is the same as 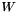 from above for Backward Euler, but again we should not infer that
from above for Backward Euler, but again we should not infer that  or
or  . However the major drawback is the mass matrix,
. However the major drawback is the mass matrix,  , the Jacobian,
, the Jacobian,  , and the residual,
, and the residual,  (i.e., the ModelEvaluator) are explicitly written only for Backward Euler. The application would need to write separate ModelEvaluators for each stepper, thus destroying the ability to re-use the ModelEvaluator with any stepper.
(i.e., the ModelEvaluator) are explicitly written only for Backward Euler. The application would need to write separate ModelEvaluators for each stepper, thus destroying the ability to re-use the ModelEvaluator with any stepper.
Definition at line 227 of file Tempus_StepperImplicit_decl.hpp.
|
virtual |
Reimplemented from Tempus::Stepper< Scalar >.
Reimplemented in Tempus::StepperIMEX_RK_Partition< Scalar >, Tempus::StepperIMEX_RK< Scalar >, Tempus::StepperDIRK< Scalar >, Tempus::StepperBackwardEuler< Scalar >, Tempus::StepperBDF2< Scalar >, Tempus::StepperNewmarkImplicitAForm< Scalar >, Tempus::StepperTrapezoidal< Scalar >, Tempus::StepperNewmarkImplicitDForm< Scalar >, and Tempus::StepperHHTAlpha< Scalar >.
Definition at line 318 of file Tempus_StepperImplicit_impl.hpp.
| void Tempus::StepperImplicit< Scalar >::evaluateImplicitODE | ( | Teuchos::RCP< Thyra::VectorBase< Scalar > > & | f, |
| const Teuchos::RCP< Thyra::VectorBase< Scalar > > & | x, | ||
| const Teuchos::RCP< Thyra::VectorBase< Scalar > > & | xDot, | ||
| const Scalar | time, | ||
| const Teuchos::RCP< ImplicitODEParameters< Scalar > > & | p | ||
| ) |
Evaluate implicit ODE residual, f(x, xDot, t, p).
Definition at line 292 of file Tempus_StepperImplicit_impl.hpp.
|
pure virtual |
Return alpha = d(xDot)/dx.
Implemented in Tempus::StepperIMEX_RK_Partition< Scalar >, Tempus::StepperIMEX_RK< Scalar >, Tempus::StepperDIRK< Scalar >, Tempus::StepperBackwardEuler< Scalar >, Tempus::StepperBDF2< Scalar >, Tempus::StepperNewmarkImplicitAForm< Scalar >, Tempus::StepperTrapezoidal< Scalar >, Tempus::StepperNewmarkImplicitDForm< Scalar >, and Tempus::StepperHHTAlpha< Scalar >.
|
pure virtual |
Return beta = d(x)/dx.
Implemented in Tempus::StepperIMEX_RK_Partition< Scalar >, Tempus::StepperIMEX_RK< Scalar >, Tempus::StepperDIRK< Scalar >, Tempus::StepperBackwardEuler< Scalar >, Tempus::StepperBDF2< Scalar >, Tempus::StepperNewmarkImplicitAForm< Scalar >, Tempus::StepperTrapezoidal< Scalar >, Tempus::StepperNewmarkImplicitDForm< Scalar >, and Tempus::StepperHHTAlpha< Scalar >.
|
inlinevirtual |
Implements Tempus::Stepper< Scalar >.
Definition at line 300 of file Tempus_StepperImplicit_decl.hpp.
|
inlinevirtual |
Reimplemented from Tempus::Stepper< Scalar >.
Reimplemented in Tempus::StepperIMEX_RK_Partition< Scalar >, and Tempus::StepperIMEX_RK< Scalar >.
Definition at line 236 of file Tempus_StepperImplicit_decl.hpp.
|
inlinevirtual |
Get solver.
Reimplemented from Tempus::Stepper< Scalar >.
Definition at line 252 of file Tempus_StepperImplicit_decl.hpp.
|
inlinevirtual |
Definition at line 244 of file Tempus_StepperImplicit_decl.hpp.
|
inlinevirtual |
Definition at line 298 of file Tempus_StepperImplicit_decl.hpp.
|
virtual |
Reimplemented from Tempus::Stepper< Scalar >.
Reimplemented in Tempus::StepperIMEX_RK_Partition< Scalar >, Tempus::StepperIMEX_RK< Scalar >, Tempus::StepperDIRK< Scalar >, Tempus::StepperBackwardEuler< Scalar >, Tempus::StepperBDF2< Scalar >, Tempus::StepperNewmarkImplicitAForm< Scalar >, Tempus::StepperTrapezoidal< Scalar >, Tempus::StepperNewmarkImplicitDForm< Scalar >, and Tempus::StepperHHTAlpha< Scalar >.
Definition at line 331 of file Tempus_StepperImplicit_impl.hpp.
|
virtual |
Definition at line 203 of file Tempus_StepperImplicit_impl.hpp.
|
virtual |
Set the initial conditions and make them consistent.
Implements Tempus::Stepper< Scalar >.
Reimplemented in Tempus::StepperIMEX_RK_Partition< Scalar >, Tempus::StepperIMEX_RK< Scalar >, Tempus::StepperDIRK< Scalar >, Tempus::StepperBackwardEuler< Scalar >, Tempus::StepperBDF2< Scalar >, Tempus::StepperNewmarkImplicitAForm< Scalar >, Tempus::StepperTrapezoidal< Scalar >, Tempus::StepperHHTAlpha< Scalar >, and Tempus::StepperNewmarkImplicitDForm< Scalar >.
Definition at line 36 of file Tempus_StepperImplicit_impl.hpp.
|
inlinevirtual |
Pass initial guess to Newton solver (only relevant for implicit solvers)
Implements Tempus::Stepper< Scalar >.
Definition at line 285 of file Tempus_StepperImplicit_decl.hpp.
|
virtual |
Reimplemented from Tempus::Stepper< Scalar >.
Reimplemented in Tempus::StepperIMEX_RK_Partition< Scalar >, Tempus::StepperIMEX_RK< Scalar >, Tempus::StepperBDF2< Scalar >, Tempus::StepperNewmarkImplicitAForm< Scalar >, and Tempus::StepperHHTAlpha< Scalar >.
Definition at line 20 of file Tempus_StepperImplicit_impl.hpp.
|
virtual |
Set solver.
Reimplemented from Tempus::Stepper< Scalar >.
Definition at line 217 of file Tempus_StepperImplicit_impl.hpp.
|
inlinevirtual |
Set parameter so that the initial guess is set to zero (=True) or use last timestep (=False).
Definition at line 293 of file Tempus_StepperImplicit_decl.hpp.
| const Thyra::SolveStatus< Scalar > Tempus::StepperImplicit< Scalar >::solveImplicitODE | ( | const Teuchos::RCP< Thyra::VectorBase< Scalar > > & | x | ) |
Solve problem using x in-place. (Needs to be deprecated!)
Definition at line 232 of file Tempus_StepperImplicit_impl.hpp.
| const Thyra::SolveStatus< Scalar > Tempus::StepperImplicit< Scalar >::solveImplicitODE | ( | const Teuchos::RCP< Thyra::VectorBase< Scalar > > & | x, |
| const Teuchos::RCP< Thyra::VectorBase< Scalar > > & | xDot, | ||
| const Scalar | time, | ||
| const Teuchos::RCP< ImplicitODEParameters< Scalar > > & | p | ||
| ) |
Solve implicit ODE, f(x, xDot, t, p) = 0.
Definition at line 246 of file Tempus_StepperImplicit_impl.hpp.
|
protected |
Definition at line 317 of file Tempus_StepperImplicit_decl.hpp.
|
protected |
Definition at line 316 of file Tempus_StepperImplicit_decl.hpp.
|
protected |
Definition at line 320 of file Tempus_StepperImplicit_decl.hpp.
|
protected |
Definition at line 315 of file Tempus_StepperImplicit_decl.hpp.
|
protected |
Definition at line 318 of file Tempus_StepperImplicit_decl.hpp.