|
Anasazi
Version of the Day
|
|
Anasazi
Version of the Day
|
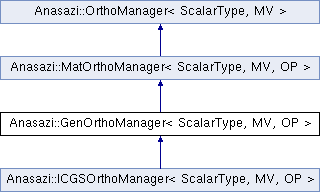
#include <AnasaziGenOrthoManager.hpp>
Public Member Functions | |
Constructor/Destructor | |
| GenOrthoManager (Teuchos::RCP< const OP > Op=Teuchos::null) | |
| Default constructor. More... | |
| virtual | ~GenOrthoManager () |
| Destructor. More... | |
Orthogonalization methods | |
| virtual void | projectGen (MV &S, Teuchos::Array< Teuchos::RCP< const MV > > X, Teuchos::Array< Teuchos::RCP< const MV > > Y, bool isBiOrtho, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< MV > MS=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MX=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null)), Teuchos::Array< Teuchos::RCP< const MV > > MY=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const =0 |
| Applies a series of generic projectors. More... | |
| virtual int | projectAndNormalizeGen (MV &S, Teuchos::Array< Teuchos::RCP< const MV > > X, Teuchos::Array< Teuchos::RCP< const MV > > Y, bool isBiOrtho, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null, Teuchos::RCP< MV > MS=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MX=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null)), Teuchos::Array< Teuchos::RCP< const MV > > MY=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const =0 |
| Applies a series of generic projectors and returns an orthonormal basis for the residual data. More... | |
 Public Member Functions inherited from Anasazi::MatOrthoManager< ScalarType, MV, OP > Public Member Functions inherited from Anasazi::MatOrthoManager< ScalarType, MV, OP > | |
| MatOrthoManager (Teuchos::RCP< const OP > Op=Teuchos::null) | |
| Default constructor. More... | |
| virtual | ~MatOrthoManager () |
| Destructor. More... | |
| virtual void | setOp (Teuchos::RCP< const OP > Op) |
| Set operator used for inner product. More... | |
| virtual Teuchos::RCP< const OP > | getOp () const |
| Get operator used for inner product. More... | |
| int | getOpCounter () const |
| Retrieve operator counter. More... | |
| void | resetOpCounter () |
| Reset the operator counter to zero. More... | |
| void | innerProdMat (const MV &X, const MV &Y, Teuchos::SerialDenseMatrix< int, ScalarType > &Z, Teuchos::RCP< const MV > MX=Teuchos::null, Teuchos::RCP< const MV > MY=Teuchos::null) const |
| Provides a matrix-based inner product. More... | |
| void | normMat (const MV &X, std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > &normvec, Teuchos::RCP< const MV > MX=Teuchos::null) const |
| Provides the norm induced by the matrix-based inner product. More... | |
| virtual void | projectMat (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< MV > MX=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MQ=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const =0 |
| Provides matrix-based projection method. More... | |
| virtual int | normalizeMat (MV &X, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null, Teuchos::RCP< MV > MX=Teuchos::null) const =0 |
| Provides matrix-based orthonormalization method. More... | |
| virtual int | projectAndNormalizeMat (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null, Teuchos::RCP< MV > MX=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MQ=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const =0 |
| Provides matrix-based projection/orthonormalization method. More... | |
| virtual Teuchos::ScalarTraits < ScalarType >::magnitudeType | orthonormErrorMat (const MV &X, Teuchos::RCP< const MV > MX=Teuchos::null) const =0 |
| This method computes the error in orthonormality of a multivector. More... | |
| virtual Teuchos::ScalarTraits < ScalarType >::magnitudeType | orthogErrorMat (const MV &X, const MV &Y, Teuchos::RCP< const MV > MX=Teuchos::null, Teuchos::RCP< const MV > MY=Teuchos::null) const =0 |
| This method computes the error in orthogonality of two multivectors. More... | |
| void | innerProd (const MV &X, const MV &Y, Teuchos::SerialDenseMatrix< int, ScalarType > &Z) const |
| Implements the interface OrthoManager::innerProd(). More... | |
| void | norm (const MV &X, std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > &normvec) const |
| Implements the interface OrthoManager::norm(). More... | |
| void | project (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null))) const |
| Implements the interface OrthoManager::project(). More... | |
| int | normalize (MV &X, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null) const |
| Implements the interface OrthoManager::normalize(). More... | |
| int | projectAndNormalize (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null) const |
| Implements the interface OrthoManager::projectAndNormalize(). More... | |
| Teuchos::ScalarTraits < ScalarType >::magnitudeType | orthonormError (const MV &X) const |
| Implements the interface OrthoManager::orthonormError(). More... | |
| Teuchos::ScalarTraits < ScalarType >::magnitudeType | orthogError (const MV &X1, const MV &X2) const |
| Implements the interface OrthoManager::orthogError(). More... | |
 Public Member Functions inherited from Anasazi::OrthoManager< ScalarType, MV > Public Member Functions inherited from Anasazi::OrthoManager< ScalarType, MV > | |
| OrthoManager () | |
| Default constructor. More... | |
| virtual | ~OrthoManager () |
| Destructor. More... | |
This class provides an interface for orthogonalization managers to provide oblique projectors of the form:
![\[ P_{X,Y} S = S - X \langle Y, X \rangle^{-1} \langle Y, S \rangle\ . \]](form_31.png)
Such a projector modifies the input in the range on 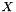 in order to make the output orthogonal to the range of
in order to make the output orthogonal to the range of 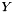 .
.
Definition at line 72 of file AnasaziGenOrthoManager.hpp.
| Anasazi::GenOrthoManager< ScalarType, MV, OP >::GenOrthoManager | ( | Teuchos::RCP< const OP > | Op = Teuchos::null | ) |
Default constructor.
Definition at line 289 of file AnasaziGenOrthoManager.hpp.
|
inlinevirtual |
Destructor.
Definition at line 80 of file AnasaziGenOrthoManager.hpp.
|
pure virtual |
Applies a series of generic projectors.
Given a list of bases X[i] and Y[i] (a projection pair), this method takes a multivector S and applies the projectors
![\[ P_{X[i],Y[i]} S = S - X[i] \langle Y[i], X[i] \rangle^{-1} \langle Y[i], S \rangle\ . \]](form_34.png)
This operation projects S onto the space orthogonal to the Y[i], along the range of the X[i]. The inner product specified by 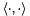 is given by innerProd().
is given by innerProd().
The method also returns the coefficients C[i] associated with each projection pair, so that
![\[ S_{in} = S_{out} + \sum_i X[i] C[i] \]](form_36.png)
and therefore
![\[ C[i] = \langle Y[i], X[i] \rangle^{-1} \langle Y[i], S \rangle\ . \]](form_37.png)
Lastly, for reasons of efficiency, the user must specify whether the projection pairs are bi-orthonormal with respect to innerProd(), i.e., whether ![$\langle Y[i], X[i] \rangle = I$](form_38.png) . In the case that the bases are specified to be biorthogonal, the inverse
. In the case that the bases are specified to be biorthogonal, the inverse 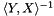 will not be computed. Furthermore, the user may optionally specifiy the image of
will not be computed. Furthermore, the user may optionally specifiy the image of S and the projection pairs under the inner product operator getOp().
| S | [in/out] The multivector to be modified. On output, the columns of S will be orthogonal to each Y[i], satisfying
|
| X | [in] Multivectors for bases under which 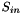 is modified. is modified. |
| Y | [in] Multivectors for bases to which 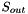 should be orthogonal. should be orthogonal. |
| isBiortho | [in] A flag specifying whether the bases X[i] and Y[i] are biorthonormal, i.e,. whether ![$\langle Y[i], X[i]\rangle == I$](form_43.png) . . |
| C | [out] Coefficients for reconstructing 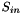 via the bases via the bases X[i]. If C[i] is a non-null pointer and C[i] matches the dimensions of S and X[i], then the coefficients computed during the orthogonalization routine will be stored in the matrix C[i].If C[i] points to a Teuchos::SerialDenseMatrix with size inconsistent with S and Otherwise, if C.size() < i or C[i] is a null pointer, the caller will not have access to the computed coefficients C[i]. |
| MS | [in/out] If specified by the user, on input MS is required to be the image of S under the operator getOp(). On output, MS will be updated to reflect the changes in S. |
| MX | [in] If specified by the user, MX[i] is required to be the image of X[i] under the operator getOp(). |
| MY | [in] If specified by the user, MY[i] is required to be the image of Y[i] under the operator getOp(). |
X[i] != Teuchos::null or Y[i] != Teuchos::null, then X[i] and Y[i] are required to have the same number of columns, and each should have the same number of rows as S. i != j, ![$\langle Y[i], X[j] \rangle == 0$](form_44.png) .
. biOrtho == true, ![$\langle Y[i], X[i]\rangle == I$](form_43.png)
biOrtho == false, then ![$\langle Y[i], X[i]\rangle$](form_45.png) should be Hermitian positive-definite.
should be Hermitian positive-definite. X[i] and Y[i] have 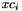 columns and
columns and S has 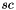 columns, then
columns, then C[i] if specified must be 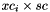 .
. Implemented in Anasazi::ICGSOrthoManager< ScalarType, MV, OP >.
|
pure virtual |
Applies a series of generic projectors and returns an orthonormal basis for the residual data.
Given a list of bases X[i] and Y[i] (a projection pair), this method takes a multivector S and applies the projectors
![\[ P_{X[i],Y[i]} S = S - X[i] \langle Y[i], X[i] \rangle^{-1} \langle Y[i], S \rangle\ . \]](form_34.png)
These operation project S onto the space orthogonal to the range of the Y[i], along the range of X[i]. The inner product specified by 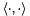 is given by innerProd().
is given by innerProd().
The method returns in S an orthonormal basis for the residual
![\[ \left( \prod_{i} P_{X[i],Y[i]} \right) S_{in} = S_{out} B\ , \]](form_49.png)
where B contains the (not necessarily triangular) coefficients of the residual with respect to the new basis.
The method also returns the coefficients C[i] and B associated with each projection pair, so that
![\[ S_{in} = S_{out} B + \sum_i X[i] C[i] \]](form_50.png)
and
![\[ C[i] = \langle Y[i], X[i] \rangle^{-1} \langle Y[i], S \rangle\ . \]](form_37.png)
Lastly, for reasons of efficiency, the user must specify whether the projection pairs are bi-orthonormal with respect to innerProd(), i.e., whether ![$\langle Y[i], X[i] \rangle = I$](form_38.png) . Furthermore, the user may optionally specifiy the image of
. Furthermore, the user may optionally specifiy the image of S and the projection pairs under the inner product operator getOp().
| S | [in/out] The multivector to be modified. On output, the columns of S will be orthogonal to each Y[i], satisfying
m is the number of rows in S, n is the number of columns in S, and rank is the value returned from the method. |
| X | [in] Multivectors for bases under which 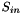 is modified. is modified. |
| Y | [in] Multivectors for bases to which 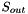 should be orthogonal. should be orthogonal. |
| isBiortho | [in] A flag specifying whether the bases X[i] and Y[i] are biorthonormal, i.e,. whether ![$\langle Y[i], X[i]\rangle == I$](form_43.png) . . |
| C | [out] Coefficients for reconstructing 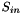 via the bases via the bases X[i]. If C[i] is a non-null pointer and C[i] matches the dimensions of X and Q[i], then the coefficients computed during the orthogonalization routine will be stored in the matrix C[i].If C[i] points to a Teuchos::SerialDenseMatrix with size inconsistent with S and Otherwise, if C.size() < i or C[i] is a null pointer, the caller will not have access to the computed coefficients C[i]. |
| B | [out] The coefficients of the original S with respect to the computed basis. If B is a non-null pointer and B matches the dimensions of B, then the coefficients computed during the orthogonalization routine will be stored in B, similar to calling innerProd( Sout, Sin, B );
B points to a Teuchos::SerialDenseMatrix with size inconsistent with S, then a std::invalid_argument exception will be thrown.Otherwise, if B is null, the caller will not have access to the computed coefficients. |
| MS | [in/out] If specified by the user, on input MS is required to be the image of S under the operator getOp(). On output, MS will be updated to reflect the changes in S. |
| MX | [in] If specified by the user, MX[i] is required to be the image of X[i] under the operator getOp(). |
| MY | [in] If specified by the user, MY[i] is required to be the image of Y[i] under the operator getOp(). |
B is not necessarily triangular (as in a QR factorization); see the documentation of specific orthogonalization managers.X[i] != Teuchos::null or Y[i] != Teuchos::null, then X[i] and Y[i] are required to have the same number of columns, and each should have the same number of rows as S. i != j, ![$\langle Y[i], X[j] \rangle == 0$](form_44.png) .
. biOrtho == true, ![$\langle Y[i], X[i]\rangle == I$](form_43.png)
biOrtho == false, then ![$\langle Y[i], X[i]\rangle$](form_45.png) should be Hermitian positive-definite.
should be Hermitian positive-definite. X[i] and Y[i] have 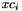 columns and
columns and S has 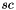 columns, then
columns, then C[i] if specified must be 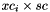 .
. S has 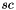 columns, then
columns, then B if specified must be 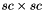 .
. Implemented in Anasazi::ICGSOrthoManager< ScalarType, MV, OP >.
 1.8.5
1.8.5