|
Anasazi
Version of the Day
|
|
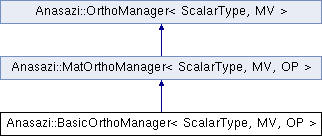
Anasazi
Version of the Day
|
An implementation of the Anasazi::MatOrthoManager that performs orthogonalization using (potentially) multiple steps of classical Gram-Schmidt. More...
#include <AnasaziBasicOrthoManager.hpp>
Public Member Functions | |
Constructor/Destructor | |
| BasicOrthoManager (Teuchos::RCP< const OP > Op=Teuchos::null, typename Teuchos::ScalarTraits< ScalarType >::magnitudeType kappa=1.41421356, typename Teuchos::ScalarTraits< ScalarType >::magnitudeType eps=0.0, typename Teuchos::ScalarTraits< ScalarType >::magnitudeType tol=0.20) | |
| Constructor specifying re-orthogonalization tolerance. More... | |
| ~BasicOrthoManager () | |
| Destructor. More... | |
Methods implementing Anasazi::MatOrthoManager | |
| void | projectMat (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< MV > MX=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MQ=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const |
Given a list of mutually orthogonal and internally orthonormal bases Q, this method projects a multivector X onto the space orthogonal to the individual Q[i], optionally returning the coefficients of X for the individual Q[i]. All of this is done with respect to the inner product innerProd(). More... | |
| int | normalizeMat (MV &X, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null, Teuchos::RCP< MV > MX=Teuchos::null) const |
This method takes a multivector X and attempts to compute an orthonormal basis for 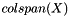 , with respect to innerProd(). More... , with respect to innerProd(). More... | |
| int | projectAndNormalizeMat (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null, Teuchos::RCP< MV > MX=Teuchos::null, Teuchos::Array< Teuchos::RCP< const MV > > MQ=Teuchos::tuple(Teuchos::RCP< const MV >(Teuchos::null))) const |
Given a set of bases Q[i] and a multivector X, this method computes an orthonormal basis for ![$colspan(X) - \sum_i colspan(Q[i])$](form_16.png) . More... . More... | |
Error methods | |
| Teuchos::ScalarTraits < ScalarType >::magnitudeType | orthonormErrorMat (const MV &X, Teuchos::RCP< const MV > MX=Teuchos::null) const |
This method computes the error in orthonormality of a multivector, measured as the Frobenius norm of the difference innerProd(X,Y) - I. The method has the option of exploiting a caller-provided MX. More... | |
| Teuchos::ScalarTraits < ScalarType >::magnitudeType | orthogErrorMat (const MV &X1, const MV &X2, Teuchos::RCP< const MV > MX1, Teuchos::RCP< const MV > MX2) const |
This method computes the error in orthogonality of two multivectors, measured as the Frobenius norm of innerProd(X,Y). The method has the option of exploiting a caller-provided MX. More... | |
Accessor routines | |
| void | setKappa (typename Teuchos::ScalarTraits< ScalarType >::magnitudeType kappa) |
| Set parameter for re-orthogonalization threshold. More... | |
| Teuchos::ScalarTraits < ScalarType >::magnitudeType | getKappa () const |
| Return parameter for re-orthogonalization threshold. More... | |
 Public Member Functions inherited from Anasazi::MatOrthoManager< ScalarType, MV, OP > Public Member Functions inherited from Anasazi::MatOrthoManager< ScalarType, MV, OP > | |
| MatOrthoManager (Teuchos::RCP< const OP > Op=Teuchos::null) | |
| Default constructor. More... | |
| virtual | ~MatOrthoManager () |
| Destructor. More... | |
| virtual void | setOp (Teuchos::RCP< const OP > Op) |
| Set operator used for inner product. More... | |
| virtual Teuchos::RCP< const OP > | getOp () const |
| Get operator used for inner product. More... | |
| int | getOpCounter () const |
| Retrieve operator counter. More... | |
| void | resetOpCounter () |
| Reset the operator counter to zero. More... | |
| void | innerProdMat (const MV &X, const MV &Y, Teuchos::SerialDenseMatrix< int, ScalarType > &Z, Teuchos::RCP< const MV > MX=Teuchos::null, Teuchos::RCP< const MV > MY=Teuchos::null) const |
| Provides a matrix-based inner product. More... | |
| void | normMat (const MV &X, std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > &normvec, Teuchos::RCP< const MV > MX=Teuchos::null) const |
| Provides the norm induced by the matrix-based inner product. More... | |
| void | innerProd (const MV &X, const MV &Y, Teuchos::SerialDenseMatrix< int, ScalarType > &Z) const |
| Implements the interface OrthoManager::innerProd(). More... | |
| void | norm (const MV &X, std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > &normvec) const |
| Implements the interface OrthoManager::norm(). More... | |
| void | project (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null))) const |
| Implements the interface OrthoManager::project(). More... | |
| int | normalize (MV &X, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null) const |
| Implements the interface OrthoManager::normalize(). More... | |
| int | projectAndNormalize (MV &X, Teuchos::Array< Teuchos::RCP< const MV > > Q, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C=Teuchos::tuple(Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >(Teuchos::null)), Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B=Teuchos::null) const |
| Implements the interface OrthoManager::projectAndNormalize(). More... | |
| Teuchos::ScalarTraits < ScalarType >::magnitudeType | orthonormError (const MV &X) const |
| Implements the interface OrthoManager::orthonormError(). More... | |
| Teuchos::ScalarTraits < ScalarType >::magnitudeType | orthogError (const MV &X1, const MV &X2) const |
| Implements the interface OrthoManager::orthogError(). More... | |
 Public Member Functions inherited from Anasazi::OrthoManager< ScalarType, MV > Public Member Functions inherited from Anasazi::OrthoManager< ScalarType, MV > | |
| OrthoManager () | |
| Default constructor. More... | |
| virtual | ~OrthoManager () |
| Destructor. More... | |
An implementation of the Anasazi::MatOrthoManager that performs orthogonalization using (potentially) multiple steps of classical Gram-Schmidt.
Definition at line 71 of file AnasaziBasicOrthoManager.hpp.
| Anasazi::BasicOrthoManager< ScalarType, MV, OP >::BasicOrthoManager | ( | Teuchos::RCP< const OP > | Op = Teuchos::null, |
| typename Teuchos::ScalarTraits< ScalarType >::magnitudeType | kappa = 1.41421356, |
||
| typename Teuchos::ScalarTraits< ScalarType >::magnitudeType | eps = 0.0, |
||
| typename Teuchos::ScalarTraits< ScalarType >::magnitudeType | tol = 0.20 |
||
| ) |
Constructor specifying re-orthogonalization tolerance.
Definition at line 315 of file AnasaziBasicOrthoManager.hpp.
|
inline |
Destructor.
Definition at line 91 of file AnasaziBasicOrthoManager.hpp.
|
virtual |
Given a list of mutually orthogonal and internally orthonormal bases Q, this method projects a multivector X onto the space orthogonal to the individual Q[i], optionally returning the coefficients of X for the individual Q[i]. All of this is done with respect to the inner product innerProd().
After calling this routine, X will be orthogonal to each of the Q[i].
| X | [in/out] The multivector to be modified. On output, the columns of X will be orthogonal to each Q[i], satisfying
|
| MX | [in/out] The image of X under the inner product operator Op. If 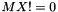 : On input, this is expected to be consistent with : On input, this is expected to be consistent with Op X. On output, this is updated consistent with updates to X. If 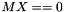 or or 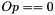 : : MX is not referenced. |
| C | [out] The coefficients of X in the bases Q[i]. If C[i] is a non-null pointer and C[i] matches the dimensions of X and Q[i], then the coefficients computed during the orthogonalization routine will be stored in the matrix C[i], similar to calling innerProd( Q[i], X, C[i] );
C[i] points to a Teuchos::SerialDenseMatrix with size inconsistent with X and C.size() < i or C[i] is a null pointer, the caller will not have access to the computed coefficients. |
| Q | [in] A list of multivector bases specifying the subspaces to be orthogonalized against, satisfying
|
Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.
Definition at line 372 of file AnasaziBasicOrthoManager.hpp.
|
virtual |
This method takes a multivector X and attempts to compute an orthonormal basis for 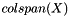 , with respect to innerProd().
, with respect to innerProd().
The method uses classical Gram-Schmidt with selective reorthogonalization. As a result, the coefficient matrix B is upper triangular.
This routine returns an integer rank stating the rank of the computed basis. If X does not have full rank and the normalize() routine does not attempt to augment the subspace, then rank may be smaller than the number of columns in X. In this case, only the first rank columns of output X and first rank rows of B will be valid.
The method attempts to find a basis with dimension equal to the number of columns in X. It does this by augmenting linearly dependent vectors in X with random directions. A finite number of these attempts will be made; therefore, it is possible that the dimension of the computed basis is less than the number of vectors in X.
| X | [in/out] The multivector to be modified. On output, the first rank columns of X satisfy
m is the number of rows in X and n is the number of columns in X. |
| MX | [in/out] The image of X under the inner product operator Op. If 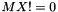 : On input, this is expected to be consistent with : On input, this is expected to be consistent with Op X. On output, this is updated consistent with updates to X. If 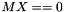 or or 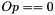 : : MX is not referenced. |
| B | [out] The coefficients of the original X with respect to the computed basis. If B is a non-null pointer and B matches the dimensions of B, then the coefficients computed during the orthogonalization routine will be stored in B, similar to calling innerProd( Xout, Xin, B );
B points to a Teuchos::SerialDenseMatrix with size inconsistent with X, then a std::invalid_argument exception will be thrown. Otherwise, if B is null, the caller will not have access to the computed coefficients. This matrix is not necessarily triangular (as in a QR factorization); see the documentation of specific orthogonalization managers.The first rows in B corresponding to the valid columns in X will be upper triangular. |
X. This specifies how many columns in the returned X and rows in the returned B are valid. Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.
Definition at line 570 of file AnasaziBasicOrthoManager.hpp.
|
virtual |
Given a set of bases Q[i] and a multivector X, this method computes an orthonormal basis for ![$colspan(X) - \sum_i colspan(Q[i])$](form_16.png) .
.
This routine returns an integer rank stating the rank of the computed basis. If the subspace ![$colspan(X) - \sum_i colspan(Q[i])$](form_16.png) does not have dimension as large as the number of columns of
does not have dimension as large as the number of columns of X and the orthogonalization manager doe not attempt to augment the subspace, then rank may be smaller than the number of columns of X. In this case, only the first rank columns of output X and first rank rows of B will be valid.
The method attempts to find a basis with dimension the same as the number of columns in X. It does this by augmenting linearly dependent vectors with random directions. A finite number of these attempts will be made; therefore, it is possible that the dimension of the computed basis is less than the number of vectors in X.
| X | [in/out] The multivector to be modified. On output, the first rank columns of X satisfy
m is the number of rows in X and n is the number of columns in X. |
| MX | [in/out] The image of X under the inner product operator Op. If 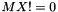 : On input, this is expected to be consistent with : On input, this is expected to be consistent with Op X. On output, this is updated consistent with updates to X. If 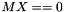 or or 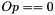 : : MX is not referenced. |
| C | [out] The coefficients of X in the Q[i]. If C[i] is a non-null pointer and C[i] matches the dimensions of X and Q[i], then the coefficients computed during the orthogonalization routine will be stored in the matrix C[i], similar to calling innerProd( Q[i], X, C[i] );
C[i] points to a Teuchos::SerialDenseMatrix with size inconsistent with X and C.size() < i or C[i] is a null pointer, the caller will not have access to the computed coefficients. |
| B | [out] The coefficients of the original X with respect to the computed basis. If B is a non-null pointer and B matches the dimensions of B, then the coefficients computed during the orthogonalization routine will be stored in B, similar to calling innerProd( Xout, Xin, B );
B points to a Teuchos::SerialDenseMatrix with size inconsistent with X, then a std::invalid_argument exception will be thrown. Otherwise, if B is null, the caller will not have access to the computed coefficients. This matrix is not necessarily triangular (as in a QR factorization); see the documentation of specific orthogonalization managers.The first rows in B corresponding to the valid columns in X will be upper triangular. |
| Q | [in] A list of multivector bases specifying the subspaces to be orthogonalized against, satisfying
|
X. This specifies how many columns in the returned X and rows in the returned B are valid. Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.
Definition at line 618 of file AnasaziBasicOrthoManager.hpp.
|
virtual |
This method computes the error in orthonormality of a multivector, measured as the Frobenius norm of the difference innerProd(X,Y) - I. The method has the option of exploiting a caller-provided MX.
Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.
Definition at line 343 of file AnasaziBasicOrthoManager.hpp.
|
virtual |
This method computes the error in orthogonality of two multivectors, measured as the Frobenius norm of innerProd(X,Y). The method has the option of exploiting a caller-provided MX.
Implements Anasazi::MatOrthoManager< ScalarType, MV, OP >.
Definition at line 360 of file AnasaziBasicOrthoManager.hpp.
|
inline |
Set parameter for re-orthogonalization threshold.
Definition at line 286 of file AnasaziBasicOrthoManager.hpp.
|
inline |
Return parameter for re-orthogonalization threshold.
Definition at line 289 of file AnasaziBasicOrthoManager.hpp.
 1.8.5
1.8.5