Use LOBPCG with Tpetra, with custom StatusTest.This example shows how to define a custom StatusTest so that Anasazi's solver LOBPCG converges correctly with spectrum folding. Without a custom status test, Anasazi would compute the residual as 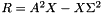 . The custom status test makes Anasazi use the residual
. The custom status test makes Anasazi use the residual 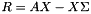 instead.
instead.
#include "Tpetra_Core.hpp"
#include "MatrixMarket_Tpetra.hpp"
using std::cout;
using std::endl;
typedef double Scalar;
typedef Tpetra::MultiVector<Scalar> TMV;
typedef Tpetra::Vector<Scalar> Vector;
typedef Tpetra::Operator<Scalar> TOP;
namespace {
class FoldOp : public TOP {
public:
typedef Tpetra::Map<> map_type;
FoldOp (const RCP<const TOP> A) { A_ = A; };
int SetUseTranspose (bool UseTranspose) { return -1; };
void
RCP<const map_type> getDomainMap () const { return A_->getDomainMap (); };
RCP<const map_type> getRangeMap () const { return A_->getRangeMap (); };
private:
RCP<const TOP> A_;
};
void
Scalar alpha, Scalar beta) const
{
TMV Y1 (X.getMap (), X.getNumVectors (), false);
A_->apply (X, Y1, mode, alpha, beta);
A_->apply (Y1, Y, mode, alpha, beta);
}
public:
StatusTestFolding (Scalar tol, int quorum = -1,
bool scaled = true,
bool throwExceptionOnNan = true,
const RCP<const TOP>& A = Teuchos::null);
virtual ~StatusTestFolding() {};
std::vector<int>
whichVecs ()
const {
return ind_; }
int howMany ()
const {
return ind_.size (); }
ind_.resize (0);
}
std::ostream&
print (std::ostream &os,
int indent=0)
const;
private:
Scalar tol_;
std::vector<int> ind_;
int quorum_;
bool scaled_;
RCP<const TOP> A_;
const Scalar ONE;
};
StatusTestFolding::
StatusTestFolding (Scalar tol, int quorum, bool scaled,
bool ,
const RCP<const TOP>& A)
tol_ (tol),
quorum_ (quorum),
scaled_ (scaled),
A_ (A),
{}
{
const int numev = X->getNumVectors ();
std::vector<Scalar> res (numev);
TMV AX (X->getMap (), numev, false);
A_->apply (*X, AX);
TMVT::MvTransMv (1.0, AX, *X, T);
TMVT::MvTimesMatAddMv (-1.0, *X, T, 1.0, AX);
TMVT::MvNorm (AX, res);
if (scaled_) {
for (int i = 0; i < numev; ++i) {
res[i] /= std::abs (T(i,i));
}
}
ind_.resize (0);
for (int i = 0; i < numev; ++i) {
if (res[i] < tol_) {
ind_.push_back (i);
}
}
const int have = ind_.size ();
const int need = (quorum_ == -1) ? numev : quorum_;
return state_;
}
std::ostream&
StatusTestFolding::print (std::ostream& os, int indent) const
{
std::string ind (indent, ' ');
os << ind << "- StatusTestFolding: ";
switch (state_) {
os << "Passed\n";
break;
os << "Failed\n";
break;
os << "Undefined\n";
break;
}
os << ind << " (Tolerance, WhichNorm,Scaled,Quorum): "
<< "(" << tol_
<< ",RES_2NORM"
<< "," << (scaled_ ? "true" : "false")
<< "," << quorum_
<< ")\n";
os << ind << " Which vectors: ";
if (ind_.size () > 0) {
for (size_t i = 0; i < ind_.size (); ++i) {
os << ind_[i] << " ";
}
os << std::endl;
}
else {
os << "[empty]\n";
}
}
return os;
}
}
int
main (int argc, char* argv[])
{
typedef Tpetra::CrsMatrix<> CrsMatrix;
typedef Tpetra::MatrixMarket::Reader<CrsMatrix> Reader;
Tpetra::ScopeGuard tpetraScope (&argc, &argv);
RCP<const Teuchos::Comm<int> > comm = Tpetra::getDefaultComm ();
const int myRank = comm->getRank();
std::string fileA ("/u/slotnick_s2/aklinvex/matrices/anderson4.mtx");
cmdp.setOption ("fileA", &fileA, "Filename for the Matrix-Market stiffness matrix.");
return -1;
}
RCP<const CrsMatrix> A = Reader::readSparseFile (fileA, comm);
RCP<FoldOp> K =
rcp (
new FoldOp (A));
int blockSize = 4;
double tol = 1e-5;
bool scaled = true;
int nev = 4;
MyPL.
set (
"Which",
"SR");
MyPL.
set (
"Maximum Restarts", 10000);
MyPL.
set (
"Maximum Iterations", 1000000);
MyPL.
set (
"Block Size", blockSize);
MyPL.
set (
"Convergence Tolerance", tol );
MyPL.
set (
"Relative Convergence Tolerance", scaled);
MyPL.
set (
"Relative Locking Tolerance", scaled);
RCP<TMV> ivec =
rcp (
new TMV (A->getRowMap (), blockSize));
TMVT::MvRandom (*ivec);
RCP<Problem> MyProblem =
rcp (
new Problem (K, ivec));
MyProblem->setHermitian (true);
MyProblem->setNEV (nev);
MyProblem->setProblem ();
RCP<StatusTestFolding> convTest =
rcp (
new StatusTestFolding (tol, nev, scaled,
true, A));
RCP<StatusTestFolding> lockTest =
rcp (
new StatusTestFolding (tol/10., 1, scaled,
true, A));
solver.setGlobalStatusTest (convTest);
solver.setLockingStatusTest (lockTest);
cout << "The solve did NOT converge." << endl;
} else if (myRank == 0) {
cout << "The solve converged." << endl;
}
std::vector<Anasazi::Value<Scalar> > evals = sol.
Evals;
RCP<TMV> evecs = sol.
Evecs;
if (numev > 0) {
std::vector<Scalar> normR (sol.
numVecs);
TMV Avec (A->getRowMap (), TMVT::GetNumberVecs (*evecs));
TOPT::Apply (*A, *evecs, Avec);
TMVT::MvTransMv (1.0, Avec, *evecs, T);
TMVT::MvTimesMatAddMv (-1.0, *evecs, T, 1.0, Avec);
TMVT::MvNorm (Avec, normR);
if (myRank == 0) {
cout.setf(std::ios_base::right, std::ios_base::adjustfield);
cout<<"Actual Eigenvalues: "<<std::endl;
cout<<"------------------------------------------------------"<<std::endl;
cout<<std::setw(16)<<"Real Part"
<<std::setw(16)<<"Error"<<std::endl;
cout<<"------------------------------------------------------"<<std::endl;
for (int i=0; i<numev; i++) {
cout<<std::setw(16)<<T(i,i)
<<std::setw(16)<<normR[i]/std::abs(T(i,i))
<<std::endl;
}
cout<<"------------------------------------------------------"<<std::endl;
}
}
return 0;
}
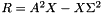 . The custom status test makes Anasazi use the residual
. The custom status test makes Anasazi use the residual 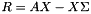 instead.
instead. 1.8.5
1.8.5