|
Tpetra parallel linear algebra
Version of the Day
|
|
Tpetra parallel linear algebra
Version of the Day
|
A class for wrapping a CrsMatrix multiply in a Operator. More...
#include <Tpetra_CrsMatrixMultiplyOp.hpp>
Public Types | |
| typedef CrsMatrix< MatScalar, LocalOrdinal, GlobalOrdinal, Node > | crs_matrix_type |
| The specialization of CrsMatrix which this class wraps. More... | |
| typedef Map< LocalOrdinal, GlobalOrdinal, Node > | map_type |
| The specialization of Map which this class uses. More... | |
Typedefs that give access to the template parameters. | |
| typedef Scalar | scalar_type |
| The type of the entries of the input and output multivectors. More... | |
| typedef LocalOrdinal | local_ordinal_type |
| The local index type. More... | |
| typedef GlobalOrdinal | global_ordinal_type |
| The global index type. More... | |
| typedef Node | node_type |
| The Kokkos Node type. More... | |
Public Member Functions | |
Constructor and destructor | |
| CrsMatrixMultiplyOp (const Teuchos::RCP< const crs_matrix_type > &A) | |
| Constructor. More... | |
| virtual | ~CrsMatrixMultiplyOp () |
| Destructor (virtual for memory safety of derived classes). More... | |
Methods implementing Operator | |
| void | apply (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &X, MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &Y, Teuchos::ETransp mode=Teuchos::NO_TRANS, Scalar alpha=Teuchos::ScalarTraits< Scalar >::one(), Scalar beta=Teuchos::ScalarTraits< Scalar >::zero()) const |
Compute Y = beta*Y + alpha*Op(A)*X, where Op(A) is either A, 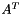 , or , or 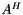 . More... . More... | |
| void | gaussSeidel (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &B, MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &D, const Scalar &dampingFactor, const ESweepDirection direction, const int numSweeps) const |
"Hybrid" Jacobi + (Gauss-Seidel or SOR) on 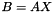 . More... . More... | |
| void | gaussSeidelCopy (MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &X, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &B, const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &D, const Scalar &dampingFactor, const ESweepDirection direction, const int numSweeps) const |
| Version of gaussSeidel(), with fewer requirements on X. More... | |
| bool | hasTransposeApply () const |
| Whether this Operator's apply() method can apply the transpose or conjugate transpose. More... | |
| Teuchos::RCP< const map_type > | getDomainMap () const |
| The domain Map of this Operator. More... | |
| Teuchos::RCP< const map_type > | getRangeMap () const |
| The range Map of this Operator. More... | |
Protected Member Functions | |
| void | applyTranspose (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &X_in, MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &Y_in, Teuchos::ETransp mode, Scalar alpha, Scalar beta) const |
| Apply the transpose or conjugate transpose of the matrix to X_in, producing Y_in. More... | |
| void | applyNonTranspose (const MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &X_in, MultiVector< Scalar, LocalOrdinal, GlobalOrdinal, Node > &Y_in, Scalar alpha, Scalar beta) const |
| Apply the matrix (not its transpose) to X_in, producing Y_in. More... | |
Protected Attributes | |
| const Teuchos::RCP< const crs_matrix_type > | matrix_ |
| The underlying CrsMatrix object. More... | |
| Teuchos::RCP< MultiVector < Scalar, LocalOrdinal, GlobalOrdinal, Node > > | importMV_ |
| Column Map MultiVector used in apply(). More... | |
| Teuchos::RCP< MultiVector < Scalar, LocalOrdinal, GlobalOrdinal, Node > > | exportMV_ |
| Row Map MultiVector used in apply(). More... | |
Related Functions | |
(Note that these are not member functions.) | |
| template<class OpScalar , class MatScalar , class LocalOrdinal , class GlobalOrdinal , class Node > | |
| Teuchos::RCP < CrsMatrixMultiplyOp < OpScalar, MatScalar, LocalOrdinal, GlobalOrdinal, Node > > | createCrsMatrixMultiplyOp (const Teuchos::RCP< const CrsMatrix< MatScalar, LocalOrdinal, GlobalOrdinal, Node > > &A) |
| Non-member function to create a CrsMatrixMultiplyOp. More... | |
A class for wrapping a CrsMatrix multiply in a Operator.
This class makes a CrsMatrix<MatScalar, ...> "look
like" an Operator<Scalar, ...>, where MatScalar and Scalar may be different types. It does so by working around a limitation of C++, namely that template methods of a class can't be virtual.
Here is a detailed description of how the language issue relates to CrsMatrix. If you call the apply method of CrsMatrix, you will always get the version that takes a MultiVector<Scalar, ...> input and produces a MultiVector<Scalar, ...> output. CrsMatrix actually implements a a templated sparse matrix-vector multiply operation (its localMultiply method). It is templated on the scalar types of its input and output multivectors (DomainScalar resp. RangeScalar). However, Operator can't access this templated mat-vec method. This is because Operator::apply is virtual, and therefore cannot have a template parameter for the Scalar type of the MultiVector input and output.
Users who want to access the templated sparse mat-vec in CrsMatrix through the Operator interface may wrap the CrsMatrix in an instance of this class. This class implements an Operator that takes MultiVector<Scalar, ...> input and output, but the CrsMatrix may contain any desired type MatScalar. The type MatScalar may differ from the Scalar type of the MultiVector input and output. That works around the "no virtual template methods" issue for input and output multivectors of the same type.
Interestingly enough, CrsMatrix implements its apply method using an instance of this class with Scalar == MatScalar. CrsMatrix does not actually contain an implementation of "nonlocal" (distributed over multiple MPI processes) mat-vec; its apply defers the nonlocal part to this class' apply() method. The same is true for the gaussSeidel() method.
| Scalar | The type of the entries of the input and output MultiVector of the apply() method. Same as the first template parameter of Operator. |
| MatScalar | The type of the entries of the CrsMatrix; the first template parameter of CrsMatrix. |
| LocalOrdinal | The type of the local indices of the CrsMatrix; the second template parameter of CrsMatrix and Operator. |
| GlobalOrdinal | The type of the global indices of the CrsMatrix; the third template parameter of CrsMatrix and Operator. |
| Node | The fourth template parameter of CrsMatrix and Operator. |
Definition at line 126 of file Tpetra_CrsMatrixMultiplyOp.hpp.
| typedef CrsMatrix<MatScalar, LocalOrdinal, GlobalOrdinal, Node> Tpetra::CrsMatrixMultiplyOp< Scalar, MatScalar, LocalOrdinal, GlobalOrdinal, Node >::crs_matrix_type |
The specialization of CrsMatrix which this class wraps.
Definition at line 131 of file Tpetra_CrsMatrixMultiplyOp.hpp.
| typedef Map<LocalOrdinal, GlobalOrdinal, Node> Tpetra::CrsMatrixMultiplyOp< Scalar, MatScalar, LocalOrdinal, GlobalOrdinal, Node >::map_type |
The specialization of Map which this class uses.
Definition at line 133 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
inherited |
The type of the entries of the input and output multivectors.
Definition at line 92 of file Tpetra_Operator.hpp.
|
inherited |
The local index type.
Definition at line 95 of file Tpetra_Operator.hpp.
|
inherited |
The global index type.
Definition at line 98 of file Tpetra_Operator.hpp.
|
inherited |
The Kokkos Node type.
Definition at line 101 of file Tpetra_Operator.hpp.
|
inline |
Constructor.
| A | [in] The CrsMatrix to wrap as an Operator<Scalar, ...>. |
Definition at line 142 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
inlinevirtual |
Destructor (virtual for memory safety of derived classes).
Definition at line 150 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
inlinevirtual |
Compute Y = beta*Y + alpha*Op(A)*X, where Op(A) is either A, 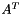 , or
, or 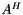 .
.
This method calls the underlying CrsMatrix object's localMultiply<Scalar,Scalar>() method.
Implements Tpetra::Operator< Scalar, LocalOrdinal, GlobalOrdinal, Node >.
Definition at line 162 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
inline |
"Hybrid" Jacobi + (Gauss-Seidel or SOR) on 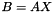 .
.
"Hybrid" means Jacobi for interprocess communication, but Successive Over-Relaxation (SOR) or Gauss-Seidel for intraprocess computation. Gauss-Seidel is a special case of SOR, where the damping factor is one.
The Forward or Backward sweep directions have their usual SOR meaning within the process. Interprocess communication occurs once before the sweep, as it would in Jacobi.
The Symmetric sweep direction means first Forward, then Backward. Before each sweep is an interprocess communication, as in Jacobi. Thus, Symmetric results in two interprocess communication steps.
| B | [in] Right-hand side(s), in the range Map of the matrix. |
| X | [in/out] On input: initial guess(es). On output: result multivector(s). This must be a domain Map view of a column Map multivector. |
| D | [in] Inverse of diagonal entries of the matrix A, in the row Map of the matrix. |
| dampingFactor | [in] SOR damping factor. A damping factor of one results in Gauss-Seidel. |
| direction | [in] Sweep direction: Forward, Backward, or Symmetric. |
| numSweeps | [in] Number of sweeps. We count each Symmetric sweep (including both its Forward and its Backward sweep) as one. |
Definition at line 225 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
inline |
Version of gaussSeidel(), with fewer requirements on X.
This method is just like gaussSeidel(), except that X need only be in the domain Map. This method does not require that X be a domain Map view of a column Map multivector. As a result, this method must copy X into a domain Map multivector before operating on it.
| X | [in/out] On input: initial guess(es). On output: result multivector(s). |
| B | [in] Right-hand side(s), in the range Map. |
| D | [in] Inverse of diagonal entries of the matrix, in the row Map. |
| dampingFactor | [in] SOR damping factor. A damping factor of one results in Gauss-Seidel. |
| direction | [in] Sweep direction: Forward, Backward, or Symmetric. |
| numSweeps | [in] Number of sweeps. We count each Symmetric sweep (including both its Forward and its Backward sweep) as one. |
Definition at line 463 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
inlinevirtual |
Whether this Operator's apply() method can apply the transpose or conjugate transpose.
This is always true, since it is true for the CrsMatrix that this object wraps.
Reimplemented from Tpetra::Operator< Scalar, LocalOrdinal, GlobalOrdinal, Node >.
Definition at line 662 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
inlinevirtual |
The domain Map of this Operator.
Implements Tpetra::Operator< Scalar, LocalOrdinal, GlobalOrdinal, Node >.
Definition at line 667 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
inlinevirtual |
The range Map of this Operator.
Implements Tpetra::Operator< Scalar, LocalOrdinal, GlobalOrdinal, Node >.
Definition at line 672 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
inlineprotected |
Apply the transpose or conjugate transpose of the matrix to X_in, producing Y_in.
Definition at line 715 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
inlineprotected |
Apply the matrix (not its transpose) to X_in, producing Y_in.
Definition at line 809 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
related |
Non-member function to create a CrsMatrixMultiplyOp.
The function has the same template parameters of CrsMatrixMultiplyOp.
| A | [in] The CrsMatrix instance to wrap in an CrsMatrixMultiplyOp. |
Definition at line 1114 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
protected |
The underlying CrsMatrix object.
Definition at line 682 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
mutableprotected |
Column Map MultiVector used in apply().
This is a column Map MultiVector. It is used as the target of the forward mode Import operation (if necessary) in applyNonTranspose(), and the source of the reverse mode Export operation (if necessary) in applyTranspose(). Both of these methods create this MultiVector on demand if needed, and reuse it (if possible) for subsequent calls.
This is declared mutable because the apply() method is const, yet the method needs to cache the MultiVector for later use.
Definition at line 696 of file Tpetra_CrsMatrixMultiplyOp.hpp.
|
mutableprotected |
Row Map MultiVector used in apply().
This is a row Map MultiVector. It is uses as the source of the forward mode Export operation (if necessary) in applyNonTranspose(), and the target of the reverse mode Import operation (if necessary) in applyTranspose(). Both of these methods create this MultiVector on demand if needed, and reuse it (if possible) for subsequent calls.
This is declared mutable because the apply() method is const, yet the method needs to cache the MultiVector for later use.
Definition at line 710 of file Tpetra_CrsMatrixMultiplyOp.hpp.
 1.8.5
1.8.5