|
Tempus
Version of the Day
Time Integration
|
|
Tempus
Version of the Day
Time Integration
|
Consider the ODE:
![\[ m\ddot{x} + c\dot{x} + kx=f \]](form_272.png)
where 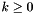 is a constant,
is a constant, 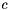 is a constant damping parameter,
is a constant damping parameter, 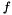 is a constant forcing parameter, and
is a constant forcing parameter, and 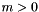 is a constant mass parameter, with initial conditions are:
is a constant mass parameter, with initial conditions are:
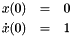
It is straight-forward to show that the exact solution to this ODE is:
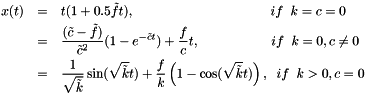
where 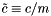 ,
, 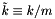 and
and 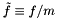 . While it is possible to derive the solution to this ODE for the case when
. While it is possible to derive the solution to this ODE for the case when 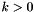 and
and 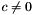 , we do not consider that case here. When
, we do not consider that case here. When 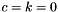 ,
, 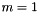 , and
, and 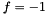 , our ODE simplies to a canonical differential equation model of a ball thrown up in the air, with a parabolic trajectory solution, namely
, our ODE simplies to a canonical differential equation model of a ball thrown up in the air, with a parabolic trajectory solution, namely
![\[ x(t) = t(1-0.5t) \]](form_287.png)
where ![$t\in [0,2]$](form_288.png) . An EpetraExt version of this simplified version of the test is implemented in Piro::MockModelEval_B (see Trilinos/packages/piro/test), where it is used to test the Piro (EpetraExt) Newmark-Beta scheme (see input_Solver_NB.xml input file). When
. An EpetraExt version of this simplified version of the test is implemented in Piro::MockModelEval_B (see Trilinos/packages/piro/test), where it is used to test the Piro (EpetraExt) Newmark-Beta scheme (see input_Solver_NB.xml input file). When 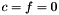 and
and 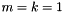 , this test is equivalent to the SinCos model..
More...
, this test is equivalent to the SinCos model..
More...
#include <HarmonicOscillatorModel_decl.hpp>

Public Member Functions | |
| HarmonicOscillatorModel (Teuchos::RCP< Teuchos::ParameterList > pList=Teuchos::null) | |
| Thyra::ModelEvaluatorBase::InArgs < Scalar > | getExactSolution (double t) const |
Public functions overridden from ModelEvaluator. | |
| Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > | get_x_space () const |
| Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > | get_f_space () const |
| Thyra::ModelEvaluatorBase::InArgs < Scalar > | getNominalValues () const |
| Teuchos::RCP < Thyra::LinearOpWithSolveBase < Scalar > > | create_W () const |
| Teuchos::RCP < Thyra::LinearOpBase< Scalar > > | create_W_op () const |
| Teuchos::RCP< const Thyra::LinearOpWithSolveFactoryBase < Scalar > > | get_W_factory () const |
| Thyra::ModelEvaluatorBase::InArgs < Scalar > | createInArgs () const |
| Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > | get_p_space (int l) const |
| Teuchos::RCP< const Teuchos::Array< std::string > > | get_p_names (int l) const |
| Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > | get_g_space (int j) const |
Public functions overridden from ParameterListAcceptor. | |
| void | setParameterList (Teuchos::RCP< Teuchos::ParameterList > const ¶mList) |
| Teuchos::RCP< const Teuchos::ParameterList > | getValidParameters () const |
Private Member Functions | |
| void | setupInOutArgs_ () const |
Private functions overridden from ModelEvaluatorDefaultBase. | |
| Thyra::ModelEvaluatorBase::OutArgs < Scalar > | createOutArgsImpl () const |
| void | evalModelImpl (const Thyra::ModelEvaluatorBase::InArgs< Scalar > &inArgs_bar, const Thyra::ModelEvaluatorBase::OutArgs< Scalar > &outArgs_bar) const |
Private Attributes | |
| Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > | x_space_ |
| Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > | p_space_ |
| Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > | g_space_ |
| Teuchos::RCP < Thyra::VectorBase< Scalar > > | x_vec_ |
| Teuchos::RCP < Thyra::VectorBase< Scalar > > | x_dot_vec_ |
| Teuchos::RCP < Thyra::VectorBase< Scalar > > | x_dot_dot_vec_ |
| Teuchos::RCP < Thyra::VectorBase< Scalar > > | p_init_ |
| int | vecLength_ |
| int | numResponses_ |
| Thyra::ModelEvaluatorBase::InArgs < Scalar > | inArgs_ |
| Thyra::ModelEvaluatorBase::OutArgs < Scalar > | outArgs_ |
| Thyra::ModelEvaluatorBase::InArgs < Scalar > | nominalValues_ |
| bool | isInitialized_ |
| double | c_ |
| double | f_ |
| double | k_ |
| double | m_ |
| Teuchos::RCP < Teuchos::FancyOStream > | out_ |
Consider the ODE:
![\[ m\ddot{x} + c\dot{x} + kx=f \]](form_272.png)
where 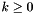 is a constant,
is a constant, 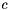 is a constant damping parameter,
is a constant damping parameter, 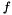 is a constant forcing parameter, and
is a constant forcing parameter, and 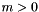 is a constant mass parameter, with initial conditions are:
is a constant mass parameter, with initial conditions are:
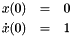
It is straight-forward to show that the exact solution to this ODE is:
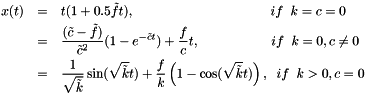
where 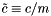 ,
, 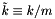 and
and 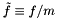 . While it is possible to derive the solution to this ODE for the case when
. While it is possible to derive the solution to this ODE for the case when 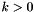 and
and 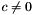 , we do not consider that case here. When
, we do not consider that case here. When 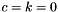 ,
, 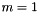 , and
, and 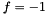 , our ODE simplies to a canonical differential equation model of a ball thrown up in the air, with a parabolic trajectory solution, namely
, our ODE simplies to a canonical differential equation model of a ball thrown up in the air, with a parabolic trajectory solution, namely
![\[ x(t) = t(1-0.5t) \]](form_287.png)
where ![$t\in [0,2]$](form_288.png) . An EpetraExt version of this simplified version of the test is implemented in Piro::MockModelEval_B (see Trilinos/packages/piro/test), where it is used to test the Piro (EpetraExt) Newmark-Beta scheme (see input_Solver_NB.xml input file). When
. An EpetraExt version of this simplified version of the test is implemented in Piro::MockModelEval_B (see Trilinos/packages/piro/test), where it is used to test the Piro (EpetraExt) Newmark-Beta scheme (see input_Solver_NB.xml input file). When 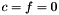 and
and 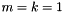 , this test is equivalent to the SinCos model..
, this test is equivalent to the SinCos model..
Definition at line 52 of file HarmonicOscillatorModel_decl.hpp.
| Tempus_Test::HarmonicOscillatorModel< Scalar >::HarmonicOscillatorModel | ( | Teuchos::RCP< Teuchos::ParameterList > | pList = Teuchos::null | ) |
Definition at line 28 of file HarmonicOscillatorModel_impl.hpp.
| Teuchos::RCP< Thyra::LinearOpWithSolveBase< Scalar > > Tempus_Test::HarmonicOscillatorModel< Scalar >::create_W | ( | ) | const |
Definition at line 155 of file HarmonicOscillatorModel_impl.hpp.
| Teuchos::RCP< Thyra::LinearOpBase< Scalar > > Tempus_Test::HarmonicOscillatorModel< Scalar >::create_W_op | ( | ) | const |
Definition at line 172 of file HarmonicOscillatorModel_impl.hpp.
| Thyra::ModelEvaluatorBase::InArgs< Scalar > Tempus_Test::HarmonicOscillatorModel< Scalar >::createInArgs | ( | ) | const |
Definition at line 193 of file HarmonicOscillatorModel_impl.hpp.
|
private |
Definition at line 206 of file HarmonicOscillatorModel_impl.hpp.
|
private |
Definition at line 216 of file HarmonicOscillatorModel_impl.hpp.
| Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > Tempus_Test::HarmonicOscillatorModel< Scalar >::get_f_space | ( | ) | const |
Definition at line 135 of file HarmonicOscillatorModel_impl.hpp.
| Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > Tempus_Test::HarmonicOscillatorModel< Scalar >::get_g_space | ( | int | j | ) | const |
Definition at line 324 of file HarmonicOscillatorModel_impl.hpp.
| Teuchos::RCP< const Teuchos::Array< std::string > > Tempus_Test::HarmonicOscillatorModel< Scalar >::get_p_names | ( | int | l | ) | const |
Definition at line 314 of file HarmonicOscillatorModel_impl.hpp.
| Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > Tempus_Test::HarmonicOscillatorModel< Scalar >::get_p_space | ( | int | l | ) | const |
Definition at line 304 of file HarmonicOscillatorModel_impl.hpp.
| Teuchos::RCP< const Thyra::LinearOpWithSolveFactoryBase< Scalar > > Tempus_Test::HarmonicOscillatorModel< Scalar >::get_W_factory | ( | ) | const |
Definition at line 182 of file HarmonicOscillatorModel_impl.hpp.
| Teuchos::RCP< const Thyra::VectorSpaceBase< Scalar > > Tempus_Test::HarmonicOscillatorModel< Scalar >::get_x_space | ( | ) | const |
Definition at line 126 of file HarmonicOscillatorModel_impl.hpp.
| Thyra::ModelEvaluatorBase::InArgs< Scalar > Tempus_Test::HarmonicOscillatorModel< Scalar >::getExactSolution | ( | double | t | ) | const |
Definition at line 69 of file HarmonicOscillatorModel_impl.hpp.
| Thyra::ModelEvaluatorBase::InArgs< Scalar > Tempus_Test::HarmonicOscillatorModel< Scalar >::getNominalValues | ( | ) | const |
Definition at line 144 of file HarmonicOscillatorModel_impl.hpp.
| Teuchos::RCP< const Teuchos::ParameterList > Tempus_Test::HarmonicOscillatorModel< Scalar >::getValidParameters | ( | ) | const |
Definition at line 414 of file HarmonicOscillatorModel_impl.hpp.
| void Tempus_Test::HarmonicOscillatorModel< Scalar >::setParameterList | ( | Teuchos::RCP< Teuchos::ParameterList > const & | paramList | ) |
Definition at line 382 of file HarmonicOscillatorModel_impl.hpp.
|
private |
Definition at line 338 of file HarmonicOscillatorModel_impl.hpp.
|
private |
Definition at line 114 of file HarmonicOscillatorModel_decl.hpp.
|
private |
Definition at line 115 of file HarmonicOscillatorModel_decl.hpp.
|
private |
Definition at line 103 of file HarmonicOscillatorModel_decl.hpp.
|
mutableprivate |
Definition at line 110 of file HarmonicOscillatorModel_decl.hpp.
|
mutableprivate |
Definition at line 113 of file HarmonicOscillatorModel_decl.hpp.
|
private |
Definition at line 116 of file HarmonicOscillatorModel_decl.hpp.
|
private |
Definition at line 117 of file HarmonicOscillatorModel_decl.hpp.
|
mutableprivate |
Definition at line 112 of file HarmonicOscillatorModel_decl.hpp.
|
private |
Definition at line 109 of file HarmonicOscillatorModel_decl.hpp.
|
private |
Definition at line 118 of file HarmonicOscillatorModel_decl.hpp.
|
mutableprivate |
Definition at line 111 of file HarmonicOscillatorModel_decl.hpp.
|
private |
Definition at line 107 of file HarmonicOscillatorModel_decl.hpp.
|
private |
Definition at line 102 of file HarmonicOscillatorModel_decl.hpp.
|
private |
Definition at line 108 of file HarmonicOscillatorModel_decl.hpp.
|
private |
Definition at line 106 of file HarmonicOscillatorModel_decl.hpp.
|
private |
Definition at line 105 of file HarmonicOscillatorModel_decl.hpp.
|
private |
Definition at line 101 of file HarmonicOscillatorModel_decl.hpp.
|
private |
Definition at line 104 of file HarmonicOscillatorModel_decl.hpp.