Interface for creating and solving a local linear problem. More...

#include <Ifpack2_Container.hpp>

Inheritance diagram for Ifpack2::Container< MatrixType >:

Public Member Functions
	Container (const Teuchos::RCP< const row_matrix_type > &matrix, const Teuchos::Array< Teuchos::Array< local_ordinal_type > > &partitions, const Teuchos::RCP< const import_type > &importer, int OverlapLevel, scalar_type DampingFactor)
	Constructor. More...

	Container (const Teuchos::RCP< const row_matrix_type > &matrix, const Teuchos::Array< local_ordinal_type > &localRows)
	Constructor for single block. More...

virtual	~Container ()
	Destructor. More...

Teuchos::ArrayView< const local_ordinal_type >	getLocalRows (int blockIndex) const
	Local indices of the rows of the input matrix that belong to this block. More...

virtual void	initialize ()=0
	Do all set-up operations that only require matrix structure. More...

void	setBlockSizes (const Teuchos::Array< Teuchos::Array< local_ordinal_type > > &partitions)
	Initialize arrays with information about block sizes. More...

virtual void	compute ()=0
	Extract the local diagonal block and prepare the solver. More...

virtual void	setParameters (const Teuchos::ParameterList &List)=0
	Set parameters. More...

virtual bool	isInitialized () const =0
	Return `true` if the container has been successfully initialized. More...

virtual bool	isComputed () const =0
	Return `true` if the container has been successfully computed. More...

virtual void	apply (HostView &X, HostView &Y, int blockIndex, int stride, Teuchos::ETransp mode=Teuchos::NO_TRANS, scalar_type alpha=Teuchos::ScalarTraits< scalar_type >::one(), scalar_type beta=Teuchos::ScalarTraits< scalar_type >::zero()) const =0
	Compute `Y := alpha * M^{-1} X + beta*Y`. More...

virtual void	applyInverseJacobi (const mv_type &, mv_type &, bool, int) const
	Compute `Y := (1 - a) Y + a D^{-1} (X - R*Y)`. More...

void	applyMV (mv_type &X, mv_type &Y) const
	Wrapper for apply with MVs, used in unit tests (never called by BlockRelaxation) More...

virtual void	weightedApply (HostView &X, HostView &Y, HostView &W, int blockIndex, int stride, Teuchos::ETransp mode=Teuchos::NO_TRANS, scalar_type alpha=Teuchos::ScalarTraits< scalar_type >::one(), scalar_type beta=Teuchos::ScalarTraits< scalar_type >::zero()) const =0
	Compute `Y := alpha * diag(D) * M^{-1} (diag(D) * X) + beta*Y`. More...

void	weightedApplyMV (mv_type &X, mv_type &Y, vector_type &W)
	Wrapper for weightedApply with MVs, used in unit tests (never called by BlockRelaxation) More...

virtual std::ostream &	print (std::ostream &os) const =0
	Print basic information about the container to `os`. More...

Static Public Member Functions
static std::string	getName ()

Protected Types
Internal typedefs (protected)
typedef MatrixType::scalar_type	scalar_type

typedef MatrixType::local_ordinal_type	local_ordinal_type

typedef MatrixType::global_ordinal_type	global_ordinal_type

typedef MatrixType::node_type	node_type

typedef Tpetra::MultiVector < scalar_type, local_ordinal_type, global_ordinal_type, node_type >	mv_type

typedef Tpetra::Vector < scalar_type, local_ordinal_type, global_ordinal_type, node_type >	vector_type

typedef Tpetra::Map < local_ordinal_type, global_ordinal_type, node_type >	map_type

typedef Teuchos::ScalarTraits < scalar_type >	STS

typedef Tpetra::Import < local_ordinal_type, global_ordinal_type, node_type >	import_type

typedef Partitioner < Tpetra::RowGraph < local_ordinal_type, global_ordinal_type, node_type > >	partitioner_type

typedef Tpetra::Experimental::BlockCrsMatrix < scalar_type, local_ordinal_type, global_ordinal_type, node_type >	block_crs_matrix_type

typedef Tpetra::RowMatrix < scalar_type, local_ordinal_type, global_ordinal_type, node_type >	row_matrix_type

typedef Kokkos::Details::ArithTraits < scalar_type >::val_type	impl_scalar_type
	Internal representation of Scalar in Kokkos::View. More...

Protected Attributes
Teuchos::RCP< const row_matrix_type >	inputMatrix_
	The input matrix to the constructor. More...

int	numBlocks_
	The number of blocks (partitions) in the container. More...

Teuchos::Array < local_ordinal_type >	partitions_
	Local indices of the rows of the input matrix that belong to this block. More...

Teuchos::Array < local_ordinal_type >	blockRows_
	Number of rows in each block. More...

Teuchos::Array < local_ordinal_type >	partitionIndices_
	Starting index in partitions_ of local row indices for each block. More...

Teuchos::RCP< vector_type >	Diag_
	Diagonal elements. More...

bool	IsParallel_
	Whether the problem is distributed across multiple MPI processes. More...

int	OverlapLevel_
	Number of rows of overlap for adjacent blocks. More...

scalar_type	DampingFactor_
	Damping factor, passed to apply() as alpha. More...

Teuchos::RCP< const Tpetra::Import < local_ordinal_type, global_ordinal_type, node_type > >	Importer_
	Importer for importing off-process elements of MultiVectors. More...

local_ordinal_type	NumLocalRows_
	Number of local rows in input matrix. More...

global_ordinal_type	NumGlobalRows_
	Number of global rows in input matrix. More...

global_ordinal_type	NumGlobalNonzeros_
	Number of nonzeros in input matrix. More...

bool	hasBlockCrs_
	Whether the input matrix is a BlockCRS matrix. More...

int	bcrsBlockSize_
	If hasBlockCrs_, the number of DOFs per vertex. Otherwise 1. More...

Detailed Description

template<class MatrixType>
class Ifpack2::Container< MatrixType >

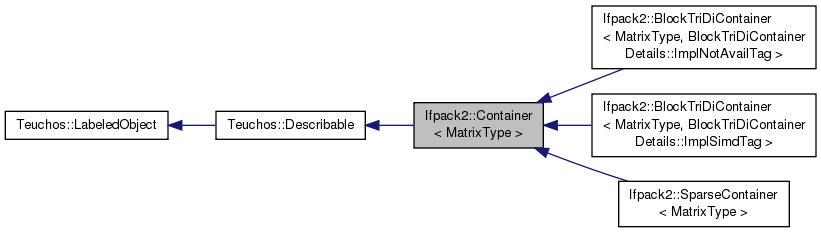
Interface for creating and solving a local linear problem.

Template Parameters

MatrixType A specialization of Tpetra::RowMatrix.

This class is mainly useful for the implementation of BlockRelaxation, and other preconditioners that need to solve linear systems with diagonal blocks of a sparse matrix.

Users of BlockRelaxation (and any analogous preconditioners) do not normally need to interact with the Container interface. However, they do need to specify a specific Container subclass to use, for example as the second template parameter (ContainerType) of BlockRelaxation. Implementations of Container specify

the kind of data structure used to store the local matrix, and
how to solve a linear system with the local matrix.

For example, the SparseContainer subclass uses a sparse matrix (in particular, Tpetra::CrsMatrix) to store each diagonal block, and can use any given Ifpack2 Preconditioner subclass to solve linear systems.

A Container can create, populate, and solve a local linear system. The local linear system matrix, B, is a submatrix of the local components of a distributed matrix, A. The idea of Container is to specify the rows of A that are contained in B, then extract B from A, and compute all it is necessary to solve a linear system in B. Then, set the initial guess (if necessary) and right-hand side for B, and solve the linear system in B.

If you are writing a class (comparable to BlockRelaxation) that uses Container, you should use it in the following way:

Create a Container object, specifying the global matrix A and the indices of the local rows of A that are contained in B. The latter indices come from a Partitioner object.
Optionally, set linear solve parameters using setParameters().
Initialize the container by calling initialize().
Prepare the linear system solver using compute().
Solve the linear system using apply().

For an example of Steps 1-5 above, see the implementation of BlockRelaxation::ExtractSubmatrices() in Ifpack2_BlockRelaxation_def.hpp.

Member Typedef Documentation

template<class MatrixType>

typedef Kokkos::Details::ArithTraits<scalar_type>::val_type Ifpack2::Container< MatrixType >::impl_scalar_type

protected

Internal representation of Scalar in Kokkos::View.

Constructor & Destructor Documentation

template<class MatrixType>

Ifpack2::Container< MatrixType >::Container	(	const Teuchos::RCP< const row_matrix_type > &	matrix,
		const Teuchos::Array< Teuchos::Array< local_ordinal_type > > &	partitions,
		const Teuchos::RCP< const import_type > &	importer,
		int	OverlapLevel,
		scalar_type	DampingFactor
	)

inline

Constructor.

matrix [in] The original input matrix. This Container will construct local diagonal blocks from the rows given by partitioner.

Parameters

partitioner [in] The Partitioner object that assigns local rows of the input matrix to blocks.

template<class MatrixType>

Ifpack2::Container< MatrixType >::Container	(	const Teuchos::RCP< const row_matrix_type > &	matrix,
		const Teuchos::Array< local_ordinal_type > &	localRows
	)

inline

Constructor for single block.

matrix [in] The original input matrix. This Container will construct a local diagonal block from the rows given by localRows.

Parameters

localRows [in] The set of (local) rows assigned to this container. localRows[i] == j, where i (from 0 to getNumRows() - 1) indicates the Container's row, and j indicates the local row in the calling process. Subclasses must always pass along these indices to the base class.

template<class MatrixType>

virtual Ifpack2::Container< MatrixType >::~Container ( )

inlinevirtual

Destructor.

Member Function Documentation

template<class MatrixType>

Teuchos::ArrayView<const local_ordinal_type> Ifpack2::Container< MatrixType >::getLocalRows ( int blockIndex ) const

inline

Local indices of the rows of the input matrix that belong to this block.

The set of (local) rows assigned to this Container is defined by passing in a set of indices localRows[i] = j to the constructor, where i (from 0 to getNumRows() - 1) indicates the Container's row, and j indicates the local row in the calling process. Subclasses must always pass along these indices to the base class.

The indices are usually used to reorder the local row index (on the calling process) of the i-th row in the Container.

For an example of how to use these indices, see the implementation of BlockRelaxation::ExtractSubmatrices() in Ifpack2_BlockRelaxation_def.hpp.

template<class MatrixType>

virtual void Ifpack2::Container< MatrixType >::initialize ( )

pure virtual

Do all set-up operations that only require matrix structure.

If the input matrix's structure changes, you must call this method before you may call compute(). You must then call compute() before you may call apply() or weightedApply().

"Structure" refers to the graph of the matrix: the local and global dimensions, and the populated entries in each row.

Implemented in Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplNotAvailTag >, Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplSimdTag >, and Ifpack2::SparseContainer< MatrixType, InverseType >.

template<class MatrixType>

void Ifpack2::Container< MatrixType >::setBlockSizes ( const Teuchos::Array< Teuchos::Array< local_ordinal_type > > & partitions )

inline

Initialize arrays with information about block sizes.

template<class MatrixType>

virtual void Ifpack2::Container< MatrixType >::compute ( )

pure virtual

Extract the local diagonal block and prepare the solver.

If any entries' values in the input matrix have changed, you must call this method before you may call apply() or weightedApply().

Implemented in Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplNotAvailTag >, Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplSimdTag >, and Ifpack2::SparseContainer< MatrixType, InverseType >.

template<class MatrixType>

virtual void Ifpack2::Container< MatrixType >::setParameters ( const Teuchos::ParameterList & List )

pure virtual

Set parameters.

Implemented in Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplNotAvailTag >, Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplSimdTag >, and Ifpack2::SparseContainer< MatrixType, InverseType >.

template<class MatrixType>

virtual bool Ifpack2::Container< MatrixType >::isInitialized ( ) const

pure virtual

Return true if the container has been successfully initialized.

Implemented in Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplNotAvailTag >, Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplSimdTag >, and Ifpack2::SparseContainer< MatrixType, InverseType >.

template<class MatrixType>

virtual bool Ifpack2::Container< MatrixType >::isComputed ( ) const

pure virtual

Return true if the container has been successfully computed.

Implemented in Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplNotAvailTag >, Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplSimdTag >, and Ifpack2::SparseContainer< MatrixType, InverseType >.

template<class MatrixType>

virtual void Ifpack2::Container< MatrixType >::apply	(	HostView &	X,
		HostView &	Y,
		int	blockIndex,
		int	stride,
		Teuchos::ETransp	mode = `Teuchos::NO_TRANS`,
		scalar_type	alpha = `Teuchos::ScalarTraits< scalar_type >::one()`,
		scalar_type	beta = `Teuchos::ScalarTraits< scalar_type >::zero()`
	)		const

pure virtual

Compute Y := alpha * M^{-1} X + beta*Y.

X is in the domain Map of the original matrix (the argument to compute()), and Y is in the range Map of the original matrix. This method only reads resp. modifies the permuted subset of entries of X resp. Y related to the diagonal block M. That permuted subset is defined by the indices passed into the constructor.

This method is marked const for compatibility with Tpetra::Operator's method of the same name. This might require subclasses to mark some of their instance data as mutable.

Implemented in Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplNotAvailTag >, Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplSimdTag >, and Ifpack2::SparseContainer< MatrixType, InverseType >.

template<class MatrixType>

virtual void Ifpack2::Container< MatrixType >::applyInverseJacobi	(	const mv_type &	,
		mv_type &	,
		bool	,
		int
	)		const

inlinevirtual

Compute Y := (1 - a) Y + a D^{-1} (X - R*Y).

Reimplemented in Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplNotAvailTag >, and Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplSimdTag >.

template<class MatrixType>

void Ifpack2::Container< MatrixType >::applyMV	(	mv_type &	X,
		mv_type &	Y
	)		const

inline

Wrapper for apply with MVs, used in unit tests (never called by BlockRelaxation)

template<class MatrixType>

virtual void Ifpack2::Container< MatrixType >::weightedApply	(	HostView &	X,
		HostView &	Y,
		HostView &	W,
		int	blockIndex,
		int	stride,
		Teuchos::ETransp	mode = `Teuchos::NO_TRANS`,
		scalar_type	alpha = `Teuchos::ScalarTraits< scalar_type >::one()`,
		scalar_type	beta = `Teuchos::ScalarTraits< scalar_type >::zero()`
	)		const

pure virtual

Compute Y := alpha * diag(D) * M^{-1} (diag(D) * X) + beta*Y.

X is in the domain Map of the original matrix (the argument to compute()), and Y is in the range Map of the original matrix. This method only reads resp. modifies the permuted subset of entries of X resp. Y related to the diagonal block M. That permuted subset is defined by the indices passed into the constructor. The D scaling vector must have the same number of entries on each process as X and Y, but otherwise need not have the same Map. (For example, D could be locally replicated, or could be a different object on each process with a local (MPI_COMM_SELF) communicator.)

This method supports overlap techniques, such as those used in Schwarz methods.

This method is marked const by analogy with apply(), which itself is marked const for compatibility with Tpetra::Operator's method of the same name. This might require subclasses to mark some of their instance data as mutable.

Implemented in Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplNotAvailTag >, Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplSimdTag >, and Ifpack2::SparseContainer< MatrixType, InverseType >.

template<class MatrixType>

void Ifpack2::Container< MatrixType >::weightedApplyMV	(	mv_type &	X,
		mv_type &	Y,
		vector_type &	W
	)

inline

Wrapper for weightedApply with MVs, used in unit tests (never called by BlockRelaxation)

template<class MatrixType>

virtual std::ostream& Ifpack2::Container< MatrixType >::print ( std::ostream & os ) const

pure virtual

Print basic information about the container to os.

Implemented in Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplNotAvailTag >, Ifpack2::BlockTriDiContainer< MatrixType, BlockTriDiContainerDetails::ImplSimdTag >, and Ifpack2::SparseContainer< MatrixType, InverseType >.

template<class MatrixType>

static std::string Ifpack2::Container< MatrixType >::getName ( )

inlinestatic

Returns string describing the container. See Details::ContainerFactory.

Member Data Documentation

template<class MatrixType>

Teuchos::RCP<const row_matrix_type> Ifpack2::Container< MatrixType >::inputMatrix_

protected

The input matrix to the constructor.

template<class MatrixType>

int Ifpack2::Container< MatrixType >::numBlocks_

protected

The number of blocks (partitions) in the container.

template<class MatrixType>

Teuchos::Array<local_ordinal_type> Ifpack2::Container< MatrixType >::partitions_

protected

Local indices of the rows of the input matrix that belong to this block.

template<class MatrixType>

Teuchos::Array<local_ordinal_type> Ifpack2::Container< MatrixType >::blockRows_

protected

Number of rows in each block.

template<class MatrixType>

Teuchos::Array<local_ordinal_type> Ifpack2::Container< MatrixType >::partitionIndices_

protected

Starting index in partitions_ of local row indices for each block.

template<class MatrixType>

Teuchos::RCP<vector_type> Ifpack2::Container< MatrixType >::Diag_

mutableprotected

Diagonal elements.

template<class MatrixType>

bool Ifpack2::Container< MatrixType >::IsParallel_

protected

Whether the problem is distributed across multiple MPI processes.

template<class MatrixType>

int Ifpack2::Container< MatrixType >::OverlapLevel_

protected

Number of rows of overlap for adjacent blocks.

template<class MatrixType>

scalar_type Ifpack2::Container< MatrixType >::DampingFactor_

protected

Damping factor, passed to apply() as alpha.

template<class MatrixType>

Teuchos::RCP<const Tpetra::Import<local_ordinal_type, global_ordinal_type, node_type> > Ifpack2::Container< MatrixType >::Importer_

protected

Importer for importing off-process elements of MultiVectors.

template<class MatrixType>

local_ordinal_type Ifpack2::Container< MatrixType >::NumLocalRows_

protected

Number of local rows in input matrix.

template<class MatrixType>

global_ordinal_type Ifpack2::Container< MatrixType >::NumGlobalRows_

protected

Number of global rows in input matrix.

template<class MatrixType>

global_ordinal_type Ifpack2::Container< MatrixType >::NumGlobalNonzeros_

protected

Number of nonzeros in input matrix.

template<class MatrixType>

bool Ifpack2::Container< MatrixType >::hasBlockCrs_

protected

Whether the input matrix is a BlockCRS matrix.

template<class MatrixType>

int Ifpack2::Container< MatrixType >::bcrsBlockSize_

protected

If hasBlockCrs_, the number of DOFs per vertex. Otherwise 1.

The documentation for this class was generated from the following file:

Ifpack2_Container.hpp

Public Member Functions

Static Public Member Functions

Protected Types

Protected Attributes

Detailed Description

template<class MatrixType> class Ifpack2::Container< MatrixType >

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

template<class MatrixType>
class Ifpack2::Container< MatrixType >