Belos's templated virtual class for providing routines for orthogonalization and orthonormzalition of multivectors using matrix-based inner products. More...

#include <BelosIteration.hpp>

Inheritance diagram for Belos::MatOrthoManager< ScalarType, MV, OP >:

[legend]

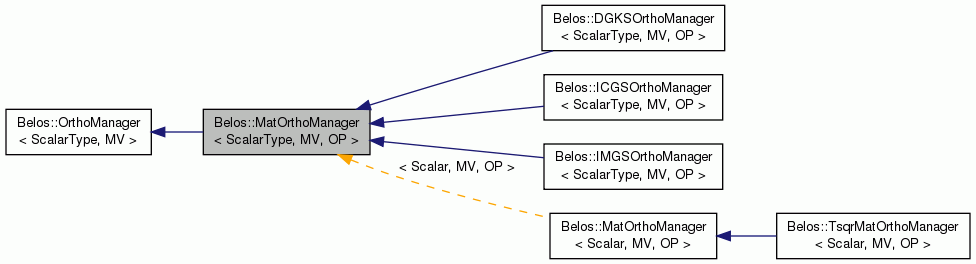
Public Member Functions
Constructor/Destructor
	MatOrthoManager (Teuchos::RCP< const OP > Op=Teuchos::null)
	Default constructor. More...

virtual	~MatOrthoManager ()
	Destructor. More...

Accessor routines
void	setOp (Teuchos::RCP< const OP > Op)
	Set operator. More...

Teuchos::RCP< const OP >	getOp () const
	Get operator. More...

Error methods
virtual Teuchos::ScalarTraits < ScalarType >::magnitudeType	orthonormError (const MV &X) const
	This method computes the error in orthonormality of a multivector. More...

virtual Teuchos::ScalarTraits < ScalarType >::magnitudeType	orthonormError (const MV &X, Teuchos::RCP< const MV > MX) const =0
	This method computes the error in orthonormality of a multivector. The method has the option of exploiting a caller-provided `MX`. More...

virtual Teuchos::ScalarTraits < ScalarType >::magnitudeType	orthogError (const MV &X1, const MV &X2) const
	This method computes the error in orthogonality of two multivectors. This method. More...

virtual Teuchos::ScalarTraits < ScalarType >::magnitudeType	orthogError (const MV &X1, Teuchos::RCP< const MV > MX1, const MV &X2) const =0
	This method computes the error in orthogonality of two multivectors. The method has the option of exploiting a caller-provided `MX`. More...

Public Member Functions inherited from Belos::OrthoManager< ScalarType, MV >
	OrthoManager ()
	Default constructor. More...

virtual	~OrthoManager ()
	Destructor. More...

virtual void	setLabel (const std::string &label)=0
	This method sets the label used by the timers in the orthogonalization manager. More...

virtual const std::string &	getLabel () const =0
	This method returns the label being used by the timers in the orthogonalization manager. More...

int	projectAndNormalize (MV &X, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B, Teuchos::ArrayView< Teuchos::RCP< const MV > > Q) const
	Project X against the Q[i] and normalize X. More...

Protected Attributes
Teuchos::RCP< const OP >	_Op

bool	_hasOp

Orthogonalization methods
void	innerProd (const MV &X, const MV &Y, Teuchos::SerialDenseMatrix< int, ScalarType > &Z) const
	Provides the inner product defining the orthogonality concepts, using the provided operator. More...

void	innerProd (const MV &X, const MV &Y, Teuchos::RCP< const MV > MY, Teuchos::SerialDenseMatrix< int, ScalarType > &Z) const
	Provides the inner product defining the orthogonality concepts, using the provided operator. The method has the options of exploiting a caller-provided `MX`. More...

void	norm (const MV &X, std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > &normvec) const
	Provides the norm induced by innerProd(). More...

void	norm (const MV &X, Teuchos::RCP< const MV > MX, std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > &normvec) const
	Compute norm of each column of X. More...

virtual void	project (MV &X, Teuchos::RCP< MV > MX, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C, Teuchos::ArrayView< Teuchos::RCP< const MV > > Q) const =0
	Given a list of (mutually and internally) orthonormal bases `Q`, this method takes a multivector `X` and projects it onto the space orthogonal to the individual `Q[i]`, optionally returning the coefficients of `X` for the individual `Q[i]`. All of this is done with respect to the inner product innerProd(). More...

virtual void	project (MV &X, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C, Teuchos::ArrayView< Teuchos::RCP< const MV > > Q) const
	This method calls project(X,Teuchos::null,C,Q); see documentation for that function. More...

virtual int	normalize (MV &X, Teuchos::RCP< MV > MX, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B) const =0
	This method takes a multivector `X` and attempts to compute an orthonormal basis for 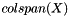, with respect to innerProd(). More...

virtual int	normalize (MV &X, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B) const
	This method calls normalize(X,Teuchos::null,B); see documentation for that function. More...

int	projectAndNormalize (MV &X, Teuchos::RCP< MV > MX, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B, Teuchos::ArrayView< Teuchos::RCP< const MV > > Q) const
	Given a set of bases `Q[i]` and a multivector `X`, this method computes an orthonormal basis for $colspan(X) - \sum_i colspan(Q[i])$ . More...

virtual int	projectAndNormalizeWithMxImpl (MV &X, Teuchos::RCP< MV > MX, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B, Teuchos::ArrayView< Teuchos::RCP< const MV > > Q) const =0

virtual int	projectAndNormalizeImpl (MV &X, Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > > C, Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > B, Teuchos::ArrayView< Teuchos::RCP< const MV > > Q) const

Detailed Description

template<class ScalarType, class MV, class OP>
class Belos::MatOrthoManager< ScalarType, MV, OP >

Belos's templated virtual class for providing routines for orthogonalization and orthonormzalition of multivectors using matrix-based inner products.

This class extends Belos::OrthoManager by providing extra calling arguments to orthogonalization routines, to reduce the cost of applying the inner product in cases where the user already has the image of the source multivector under the inner product matrix.

A concrete implementation of this class is necessary. The user can create their own implementation if those supplied are not suitable for their needs.

Author: Chris Baker, Teri Barth, and Heidi Thornquist

Definition at line 70 of file BelosIteration.hpp.

Constructor & Destructor Documentation

template<class ScalarType, class MV, class OP>

Belos::MatOrthoManager< ScalarType, MV, OP >::MatOrthoManager ( Teuchos::RCP< const OP > Op = Teuchos::null )

inline

Default constructor.

Definition at line 83 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

virtual Belos::MatOrthoManager< ScalarType, MV, OP >::~MatOrthoManager ( )

inlinevirtual

Destructor.

Definition at line 86 of file BelosMatOrthoManager.hpp.

Member Function Documentation

template<class ScalarType, class MV, class OP>

void Belos::MatOrthoManager< ScalarType, MV, OP >::setOp ( Teuchos::RCP< const OP > Op )

inline

Set operator.

Definition at line 93 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

Teuchos::RCP<const OP> Belos::MatOrthoManager< ScalarType, MV, OP >::getOp ( ) const

inline

Get operator.

Definition at line 99 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

void Belos::MatOrthoManager< ScalarType, MV, OP >::innerProd	(	const MV &	X,
		const MV &	Y,
		Teuchos::SerialDenseMatrix< int, ScalarType > &	Z
	)		const

inlinevirtual

Provides the inner product defining the orthogonality concepts, using the provided operator.

All concepts of orthogonality discussed in this class are with respect to this inner product.

Implements Belos::OrthoManager< ScalarType, MV >.

Definition at line 111 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

void Belos::MatOrthoManager< ScalarType, MV, OP >::innerProd	(	const MV &	X,
		const MV &	Y,
		Teuchos::RCP< const MV >	MY,
		Teuchos::SerialDenseMatrix< int, ScalarType > &	Z
	)		const

inline

Provides the inner product defining the orthogonality concepts, using the provided operator. The method has the options of exploiting a caller-provided MX.

If pointer MY is null, then this routine calls innerProd(X,Y,Z). Otherwise, it forgoes the operator application and uses *MY in the computation of the inner product.

Definition at line 149 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

void Belos::MatOrthoManager< ScalarType, MV, OP >::norm	(	const MV &	X,
		std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > &	normvec
	)		const

inlinevirtual

Provides the norm induced by innerProd().

Implements Belos::OrthoManager< ScalarType, MV >.

Definition at line 171 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

void Belos::MatOrthoManager< ScalarType, MV, OP >::norm	(	const MV &	X,
		Teuchos::RCP< const MV >	MX,
		std::vector< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > &	normvec
	)		const

inline

Compute norm of each column of X.

Compute the norm of each column of X; where the norm is that induced by innerProd(). If you already have MX = M*X (where M is the operator defining the inner product), you may pass it in to avoid applying the operator again.

Parameters

X	[in] Multivector for which to compute the norm of each column
MX	[in] If not null and the inner product operator M is not the identity, MX is assumed to be M*X (the result of applying the operator M to X). MX may be null, in which case if M is not the identity, it is applied to X.
normvec	[out] On output, normvec[j] is the norm of column j of X. normvec is resized if it has fewer entries than the number of columns in X.

Definition at line 193 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

virtual void Belos::MatOrthoManager< ScalarType, MV, OP >::project	(	MV &	X,
		Teuchos::RCP< MV >	MX,
		Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > >	C,
		Teuchos::ArrayView< Teuchos::RCP< const MV > >	Q
	)		const

pure virtual

Given a list of (mutually and internally) orthonormal bases Q, this method takes a multivector X and projects it onto the space orthogonal to the individual Q[i], optionally returning the coefficients of X for the individual Q[i]. All of this is done with respect to the inner product innerProd().

After calling this routine, X will be orthogonal to each of the Q[i].

Parameters

X	[in/out] The multivector to be modified. On output, `X` will be orthogonal to `Q[i]` with respect to innerProd().
MX	[in] The image of the multivector under the specified operator. If `MX` is null, it is not used.
C	[out] The coefficients of `X` in the `Q`[i], with respect to innerProd(). If `C[i]` is a non-null pointer and `C`[i] matches the dimensions of `X` and `Q`[i], then the coefficients computed during the orthogonalization routine will be stored in the matrix `C`[i]. If `C[i]` is a non-null pointer whose size does not match the dimensions of `X` and `*Q`[i], then a std::invalid_argument std::exception will be thrown. Otherwise, if `C.size() < i` or `C[i]` is a null pointer, then the orthogonalization manager will declare storage for the coefficients and the user will not have access to them.
Q	[in] A list of multivector bases specifying the subspaces to be orthogonalized against. Each `Q[i]` is assumed to have orthonormal columns, and the `Q[i]` are assumed to be mutually orthogonal.

Implemented in Belos::ICGSOrthoManager< ScalarType, MV, OP >, Belos::IMGSOrthoManager< ScalarType, MV, OP >, and Belos::DGKSOrthoManager< ScalarType, MV, OP >.

template<class ScalarType, class MV, class OP>

virtual void Belos::MatOrthoManager< ScalarType, MV, OP >::project	(	MV &	X,
		Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > >	C,
		Teuchos::ArrayView< Teuchos::RCP< const MV > >	Q
	)		const

inlinevirtual

This method calls project(X,Teuchos::null,C,Q); see documentation for that function.

Implements Belos::OrthoManager< ScalarType, MV >.

Reimplemented in Belos::ICGSOrthoManager< ScalarType, MV, OP >, Belos::IMGSOrthoManager< ScalarType, MV, OP >, and Belos::DGKSOrthoManager< ScalarType, MV, OP >.

Definition at line 275 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

virtual int Belos::MatOrthoManager< ScalarType, MV, OP >::normalize	(	MV &	X,
		Teuchos::RCP< MV >	MX,
		Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >	B
	)		const

pure virtual

This method takes a multivector X and attempts to compute an orthonormal basis for 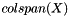$colspan(X)$ , with respect to innerProd().

This routine returns an integer rank stating the rank of the computed basis. If X does not have full rank and the normalize() routine does not attempt to augment the subspace, then rank may be smaller than the number of columns in X. In this case, only the first rank columns of output X and first rank rows of B will be valid.

Parameters

X	[in/out] The multivector to the modified. On output, `X` will have some number of orthonormal columns (with respect to innerProd()).
MX	[in/out] The image of the multivector under the specified operator. If `MX` is null, it is not used. On output, it returns the image of the valid basis vectors under the specified operator.
B	[out] The coefficients of `X` in the computed basis. If `B` is a non-null pointer and `B` has appropriate dimensions, then the coefficients computed during the orthogonalization routine will be stored in the matrix `B`. If `B` is a non-null pointer whose size does not match the dimensions of `X`, then a std::invalid_argument std::exception will be thrown. Otherwise, the orthogonalization manager will declare storage for the coefficients and the user will not have access to them. This matrix may or may not be triangular; see documentation for individual orthogonalization managers.

Returns: Rank of the basis computed by this method.

Implemented in Belos::ICGSOrthoManager< ScalarType, MV, OP >, Belos::IMGSOrthoManager< ScalarType, MV, OP >, and Belos::DGKSOrthoManager< ScalarType, MV, OP >.

template<class ScalarType, class MV, class OP>

virtual int Belos::MatOrthoManager< ScalarType, MV, OP >::normalize	(	MV &	X,
		Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >	B
	)		const

inlinevirtual

This method calls normalize(X,Teuchos::null,B); see documentation for that function.

Implements Belos::OrthoManager< ScalarType, MV >.

Reimplemented in Belos::ICGSOrthoManager< ScalarType, MV, OP >, Belos::IMGSOrthoManager< ScalarType, MV, OP >, and Belos::DGKSOrthoManager< ScalarType, MV, OP >.

Definition at line 308 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

virtual int Belos::MatOrthoManager< ScalarType, MV, OP >::projectAndNormalizeWithMxImpl	(	MV &	X,
		Teuchos::RCP< MV >	MX,
		Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > >	C,
		Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >	B,
		Teuchos::ArrayView< Teuchos::RCP< const MV > >	Q
	)		const

protectedpure virtual

Implemented in Belos::ICGSOrthoManager< ScalarType, MV, OP >, Belos::DGKSOrthoManager< ScalarType, MV, OP >, and Belos::IMGSOrthoManager< ScalarType, MV, OP >.

template<class ScalarType, class MV, class OP>

virtual int Belos::MatOrthoManager< ScalarType, MV, OP >::projectAndNormalizeImpl	(	MV &	X,
		Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > >	C,
		Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >	B,
		Teuchos::ArrayView< Teuchos::RCP< const MV > >	Q
	)		const

inlineprotectedvirtual

Implements Belos::OrthoManager< ScalarType, MV >.

Definition at line 322 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

int Belos::MatOrthoManager< ScalarType, MV, OP >::projectAndNormalize	(	MV &	X,
		Teuchos::RCP< MV >	MX,
		Teuchos::Array< Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > > >	C,
		Teuchos::RCP< Teuchos::SerialDenseMatrix< int, ScalarType > >	B,
		Teuchos::ArrayView< Teuchos::RCP< const MV > >	Q
	)		const

inline

Given a set of bases Q[i] and a multivector X, this method computes an orthonormal basis for $colspan(X) - \sum_i colspan(Q[i])$ .

This routine returns an integer rank stating the rank of the computed basis. If the subspace $colspan(X) - \sum_i colspan(Q[i])$ does not have dimension as large as the number of columns of X and the orthogonalization manager doe not attempt to augment the subspace, then rank may be smaller than the number of columns of X. In this case, only the first rank columns of output X and first rank rows of B will be valid.

Note: This routine guarantees both the orthgonality constraints against the Q[i] as well as the orthonormality constraints. Therefore, this method is not necessarily equivalent to calling project() followed by a call to normalize(); see the documentation for specific orthogonalization managers.

Parameters

X	[in/out] The multivector to the modified. On output, the relevant rows of `X` will be orthogonal to the `Q[i]` and will have orthonormal columns (with respect to innerProd()).
MX	[in/out] The image of the multivector under the specified operator. If `MX` is null, it is not used. On output, it returns the image of the valid basis vectors under the specified operator.
C	[out] The coefficients of the original `X` in the `Q`[i], with respect to innerProd(). If `C[i]` is a non-null pointer and `C`[i] matches the dimensions of `X` and `Q`[i], then the coefficients computed during the orthogonalization routine will be stored in the matrix `C`[i]. If `C[i]` is a non-null pointer whose size does not match the dimensions of `X` and `*Q`[i], then a std::invalid_argument std::exception will be thrown. Otherwise, if `C.size() < i` or `C[i]` is a null pointer, then the orthogonalization manager will declare storage for the coefficients and the user will not have access to them.
B	[out] The coefficients of `X` in the computed basis. If `B` is a non-null pointer and `B` has appropriate dimensions, then the coefficients computed during the orthogonalization routine will be stored in the matrix `B`. If `B` is a non-null pointer whose size does not match the dimensions of `X`, then a std::invalid_argument std::exception will be thrown. Otherwise, the orthogonalization manager will declare storage for the coefficients and the user will not have access to them. This matrix may or may not be triangular; see documentation for individual orthogonalization managers.
Q	[in] A list of multivector bases specifying the subspaces to be orthogonalized against. Each `Q[i]` is assumed to have orthonormal columns, and the `Q[i]` are assumed to be mutually orthogonal.

Returns: Rank of the basis computed by this method.

Definition at line 367 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

virtual Teuchos::ScalarTraits<ScalarType>::magnitudeType Belos::MatOrthoManager< ScalarType, MV, OP >::orthonormError ( const MV & X ) const

inlinevirtual

This method computes the error in orthonormality of a multivector.

Implements Belos::OrthoManager< ScalarType, MV >.

Reimplemented in Belos::TsqrMatOrthoManager< Scalar, MV, OP >, Belos::ICGSOrthoManager< ScalarType, MV, OP >, Belos::DGKSOrthoManager< ScalarType, MV, OP >, and Belos::IMGSOrthoManager< ScalarType, MV, OP >.

Definition at line 383 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

virtual Teuchos::ScalarTraits<ScalarType>::magnitudeType Belos::MatOrthoManager< ScalarType, MV, OP >::orthonormError	(	const MV &	X,
		Teuchos::RCP< const MV >	MX
	)		const

pure virtual

This method computes the error in orthonormality of a multivector. The method has the option of exploiting a caller-provided MX.

Implemented in Belos::TsqrMatOrthoManager< Scalar, MV, OP >, Belos::ICGSOrthoManager< ScalarType, MV, OP >, Belos::DGKSOrthoManager< ScalarType, MV, OP >, and Belos::IMGSOrthoManager< ScalarType, MV, OP >.

template<class ScalarType, class MV, class OP>

virtual Teuchos::ScalarTraits<ScalarType>::magnitudeType Belos::MatOrthoManager< ScalarType, MV, OP >::orthogError	(	const MV &	X1,
		const MV &	X2
	)		const

inlinevirtual

This method computes the error in orthogonality of two multivectors. This method.

Implements Belos::OrthoManager< ScalarType, MV >.

Reimplemented in Belos::TsqrMatOrthoManager< Scalar, MV, OP >, Belos::ICGSOrthoManager< ScalarType, MV, OP >, Belos::DGKSOrthoManager< ScalarType, MV, OP >, and Belos::IMGSOrthoManager< ScalarType, MV, OP >.

Definition at line 396 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

virtual Teuchos::ScalarTraits<ScalarType>::magnitudeType Belos::MatOrthoManager< ScalarType, MV, OP >::orthogError	(	const MV &	X1,
		Teuchos::RCP< const MV >	MX1,
		const MV &	X2
	)		const

pure virtual

This method computes the error in orthogonality of two multivectors. The method has the option of exploiting a caller-provided MX.

Implemented in Belos::TsqrMatOrthoManager< Scalar, MV, OP >, Belos::ICGSOrthoManager< ScalarType, MV, OP >, Belos::DGKSOrthoManager< ScalarType, MV, OP >, and Belos::IMGSOrthoManager< ScalarType, MV, OP >.

Member Data Documentation

template<class ScalarType, class MV, class OP>

Teuchos::RCP<const OP> Belos::MatOrthoManager< ScalarType, MV, OP >::_Op

protected

Definition at line 76 of file BelosMatOrthoManager.hpp.

template<class ScalarType, class MV, class OP>

bool Belos::MatOrthoManager< ScalarType, MV, OP >::_hasOp

protected

Definition at line 77 of file BelosMatOrthoManager.hpp.

The documentation for this class was generated from the following files:

Public Member Functions

Protected Attributes

Orthogonalization methods

Detailed Description

template<class ScalarType, class MV, class OP> class Belos::MatOrthoManager< ScalarType, MV, OP >

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

template<class ScalarType, class MV, class OP>
class Belos::MatOrthoManager< ScalarType, MV, OP >