|
Teko
Version of the Day
|
This linear operator computes the inverse of a upper triangular matrix. More...
#include <Teko_BlockUpperTriInverseOp.hpp>

Public Member Functions | |
| BlockUpperTriInverseOp (BlockedLinearOp &U, const std::vector< LinearOp > &invDiag) | |
| This constructor explicitly takes an upper triangular matrix and inverse diagonal operators and builds a back substitution operator. More... | |
Inherited methods from Thyra::LinearOpBase | |
| virtual VectorSpace | range () const |
| Range space of this operator. More... | |
| virtual VectorSpace | domain () const |
| Domain space of this operator. More... | |
| virtual void | implicitApply (const BlockedMultiVector &x, BlockedMultiVector &y, const double alpha=1.0, const double beta=0.0) const |
| Perform a matrix vector multiply with this operator. More... | |
| virtual void | implicitApply (const Thyra::EOpTransp M_trans, const BlockedMultiVector &x, BlockedMultiVector &y, const double alpha=1.0, const double beta=0.0) const |
| Perform a matrix vector multiply with this implicitly defined blocked operator. More... | |
Protected Attributes | |
| const BlockedLinearOp | U_ |
operator 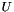 More... More... | |
| std::vector< LinearOp > | invDiag_ |
| (Approximate) Inverses of the diagonal operators More... | |
| Teuchos::RCP< const Thyra::ProductVectorSpaceBase < double > > | productRange_ |
| Range vector space. More... | |
| Teuchos::RCP< const Thyra::ProductVectorSpaceBase < double > > | productDomain_ |
| Domain vector space. More... | |
Additional Inherited Members | |
 Protected Member Functions inherited from Teko::BlockImplicitLinearOp Protected Member Functions inherited from Teko::BlockImplicitLinearOp | |
| virtual bool | opSupportedImpl (const Thyra::EOpTransp M_trans) const |
| Functions required by Thyra::LinearOpBase. More... | |
This linear operator computes the inverse of a upper triangular matrix.
This linear operator computes the inverse of an upper triangular matrix. This requires, the upper triangular blocks, as well as the inverse of the operators on the diagonal.
Definition at line 63 of file Teko_BlockUpperTriInverseOp.hpp.
| Teko::BlockUpperTriInverseOp::BlockUpperTriInverseOp | ( | BlockedLinearOp & | U, |
| const std::vector< LinearOp > & | invDiag | ||
| ) |
This constructor explicitly takes an upper triangular matrix and inverse diagonal operators and builds a back substitution operator.
This constructor explicitly takes the parts of 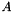 required to build the inverse operator.
required to build the inverse operator.
This constructor explicitly takes an upper triangular matrix and inverse diagonal operators and builds a back substitution operator.
| [in] | U | Upper triangular matrix object |
| [in] | invDiag | Vector containing the inverse of the diagonal blocks |
This constructor explicitly takes the parts of 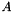 required to build the inverse operator.
required to build the inverse operator.
| [in] | A | The block 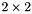 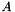 operator. operator. |
| [in] | invA00 | An approximate inverse of 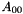 . . |
| [in] | invS | An approximate inverse of 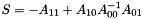 . . |
Definition at line 65 of file Teko_BlockUpperTriInverseOp.cpp.
|
inlinevirtual |
Range space of this operator.
Implements Teko::BlockImplicitLinearOp.
Definition at line 80 of file Teko_BlockUpperTriInverseOp.hpp.
|
inlinevirtual |
Domain space of this operator.
Implements Teko::BlockImplicitLinearOp.
Definition at line 83 of file Teko_BlockUpperTriInverseOp.hpp.
|
virtual |
Perform a matrix vector multiply with this operator.
The apply function takes one vector as input and applies the inverse 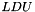 decomposition. The result is returned in
decomposition. The result is returned in 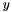 . If this operator is reprsented as
. If this operator is reprsented as 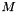 then
then 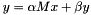 (ignoring conjugation!).
(ignoring conjugation!).
| [in] | x | |
| [in,out] | y | |
| [in] | alpha | (default=1) |
| [in] | beta | (default=0) |
Implements Teko::BlockImplicitLinearOp.
Definition at line 84 of file Teko_BlockUpperTriInverseOp.cpp.
|
virtual |
Perform a matrix vector multiply with this implicitly defined blocked operator.
Perform a matrix vector multiply with this operator.
The apply function takes one vector as input and applies a linear operator. The result is returned in 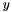 . If this operator is reprsented as
. If this operator is reprsented as 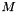 then
then 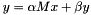
| [in] | x | |
| [in,out] | y | |
| [in] | alpha | (default=1) |
| [in] | beta | (default=0) |
The apply function takes one vector as input and applies the inverse 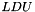 decomposition. The result is returned in
decomposition. The result is returned in 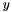 . If this operator is reprsented as
. If this operator is reprsented as 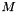 then
then 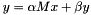 (ignoring conjugation!).
(ignoring conjugation!).
| [in] | x | |
| [in,out] | y | |
| [in] | alpha | (default=1) |
| [in] | beta | (default=0) |
Reimplemented from Teko::BlockImplicitLinearOp.
Definition at line 103 of file Teko_BlockUpperTriInverseOp.cpp.
|
protected |
operator 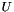
Definition at line 123 of file Teko_BlockUpperTriInverseOp.hpp.
|
protected |
(Approximate) Inverses of the diagonal operators
Definition at line 124 of file Teko_BlockUpperTriInverseOp.hpp.
|
protected |
Range vector space.
Definition at line 126 of file Teko_BlockUpperTriInverseOp.hpp.
|
protected |
Domain vector space.
Definition at line 127 of file Teko_BlockUpperTriInverseOp.hpp.
 1.8.5
1.8.5