Stub adaptor from Thyra::MultiVectorBase to TSQR. More...

#include <Thyra_TsqrAdaptor.hpp>

Inheritance diagram for Thyra::TsqrAdaptor< Scalar >:

Public Member Functions
	TsqrAdaptor (const Teuchos::RCP< Teuchos::ParameterList > &)
	Constructor (that accepts a parameter list). More...

	TsqrAdaptor ()
	Constructor (that uses default parameters). More...

void	factorExplicit (MV &, MV &, dense_matrix_type &, const bool=false)
	Compute QR factorization [Q,R] = qr(A,0). More...

int	revealRank (MV &, dense_matrix_type &, const magnitude_type &)
	Rank-revealing decomposition. More...

Detailed Description

template<class Scalar>
class Thyra::TsqrAdaptor< Scalar >

Stub adaptor from Thyra::MultiVectorBase to TSQR.

TSQR (Tall Skinny QR factorization) is an orthogonalization kernel that is as accurate as Householder QR, yet requires only 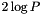$2 \log P$ messages between $P$ MPI processes, independently of the number of columns in the multivector.

TSQR works independently of the particular multivector implementation, and interfaces to the latter via an adaptor class. This class is the adaptor class for MultiVectorBase. It templates on the MultiVector (MV) type so that it can pick up that class' typedefs. In particular, TSQR chooses its intranode implementation based on the Kokkos Node type of the multivector.

Warning: This is a stub adaptor that just placates the compiler and does nothing. It's not hard to implement a Thyra adaptor, but in order for the adaptor to be efficient, it requires special cases for extracting the actual multivector implementation (e.g., Epetra_MultiVector or Tpetra::MultiVector) out of the Thyra wrapper.

Definition at line 86 of file Thyra_TsqrAdaptor.hpp.

Constructor & Destructor Documentation

template<class Scalar >

Thyra::TsqrAdaptor< Scalar >::TsqrAdaptor ( const Teuchos::RCP< Teuchos::ParameterList > & )

inline

Constructor (that accepts a parameter list).

Parameters

plist [in] List of parameters for configuring TSQR. The specific parameter keys that are read depend on the TSQR implementation. For details, call getValidParameters() and examine the documentation embedded therein.

Definition at line 100 of file Thyra_TsqrAdaptor.hpp.

template<class Scalar >

Thyra::TsqrAdaptor< Scalar >::TsqrAdaptor ( )

inline

Constructor (that uses default parameters).

Definition at line 106 of file Thyra_TsqrAdaptor.hpp.

Member Function Documentation

template<class Scalar >

void Thyra::TsqrAdaptor< Scalar >::factorExplicit	(	MV &	,
		MV &	,
		dense_matrix_type &	,
		const bool	= `false`
	)

inline

Compute QR factorization [Q,R] = qr(A,0).

Parameters

A	[in/out] On input: the multivector to factor. Overwritten with garbage on output.
Q	[out] On output: the (explicitly stored) Q factor in the QR factorization of the (input) multivector A.
R	[out] On output: the R factor in the QR factorization of the (input) multivector A.
forceNonnegativeDiagonal	[in] If true, then (if necessary) do extra work (modifying both the Q and R factors) in order to force the R factor to have a nonnegative diagonal.

Warning: Currently, this method only works if A and Q have the same communicator and row distribution ("map," in Petra terms) as those of the multivector given to this TsqrAdaptor instance's constructor. Otherwise, the result of this method is undefined.

Definition at line 145 of file Thyra_TsqrAdaptor.hpp.

template<class Scalar >

int Thyra::TsqrAdaptor< Scalar >::revealRank	(	MV &	,
		dense_matrix_type &	,
		const magnitude_type &
	)

inline

Rank-revealing decomposition.

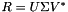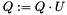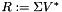Using the R factor and explicit Q factor from factorExplicit(), compute the singular value decomposition (SVD) of R ( $R = U \Sigma V^*$ ). If R is full rank (with respect to the given relative tolerance tol), don't change Q or R. Otherwise, compute $Q := Q \cdot U$ and $R := \Sigma V^*$ in place (the latter may be no longer upper triangular).

Parameters

Q	[in/out] On input: explicit Q factor computed by factorExplicit(). (Must be an orthogonal resp. unitary matrix.) On output: If R is of full numerical rank with respect to the tolerance tol, Q is unmodified. Otherwise, Q is updated so that the first rank columns of Q are a basis for the column space of A (the original matrix whose QR factorization was computed by factorExplicit()). The remaining columns of Q are a basis for the null space of A.
R	[in/out] On input: ncols by ncols upper triangular matrix with leading dimension ldr >= ncols. On output: if input is full rank, R is unchanged on output. Otherwise, if 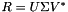$R = U \Sigma V^$ is the SVD of R, on output R is overwritten with $ V^$. This is also an ncols by ncols matrix, but may not necessarily be upper triangular.
tol	[in] Relative tolerance for computing the numerical rank of the matrix R.

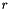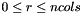Returns: Rank of R: $0 \leq r \leq ncols$ .

Definition at line 184 of file Thyra_TsqrAdaptor.hpp.

The documentation for this class was generated from the following file:

Thyra_TsqrAdaptor.hpp

Public Member Functions

Detailed Description

template<class Scalar> class Thyra::TsqrAdaptor< Scalar >

Constructor & Destructor Documentation

Member Function Documentation

template<class Scalar>
class Thyra::TsqrAdaptor< Scalar >