Ifpack_CrsRiluk: A class for constructing and using an incomplete lower/upper (ILU) factorization of a given Epetra_RowMatrix. More...

#include <Ifpack_CrsRiluk.h>

Inheritance diagram for Ifpack_CrsRiluk:

[legend]

Public Member Functions
	Ifpack_CrsRiluk (const Ifpack_IlukGraph &Graph_in)
	Ifpack_CrsRiluk constuctor with variable number of indices per row. More...

	Ifpack_CrsRiluk (const Ifpack_CrsRiluk &Matrix)
	Copy constructor. More...

virtual	~Ifpack_CrsRiluk ()
	Ifpack_CrsRiluk Destructor. More...

int	InitValues (const Epetra_CrsMatrix &A)
	Initialize L and U with values from user matrix A. More...

int	InitValues (const Epetra_VbrMatrix &A)
	Initialize L and U with values from user matrix A. More...

bool	ValuesInitialized () const
	If values have been initialized, this query returns true, otherwise it returns false. More...

void	SetRelaxValue (double RelaxValue)
	Set RILU(k) relaxation parameter. More...

void	SetAbsoluteThreshold (double Athresh)
	Set absolute threshold value. More...

void	SetRelativeThreshold (double Rthresh)
	Set relative threshold value. More...

void	SetOverlapMode (Epetra_CombineMode OverlapMode)
	Set overlap mode type. More...

int	SetParameters (const Teuchos::ParameterList &parameterlist, bool cerr_warning_if_unused=false)
	Set parameters using a Teuchos::ParameterList object. More...

int	Factor ()
	Compute ILU factors L and U using the specified graph, diagonal perturbation thresholds and relaxation parameters. More...

bool	Factored () const
	If factor is completed, this query returns true, otherwise it returns false. More...

int	Solve (bool Trans, const Epetra_MultiVector &X, Epetra_MultiVector &Y) const
	Returns the result of a Ifpack_CrsRiluk forward/back solve on a Epetra_MultiVector X in Y (works for Epetra_Vectors also). More...

int	Multiply (bool Trans, const Epetra_MultiVector &X, Epetra_MultiVector &Y) const
	Returns the result of multiplying U, D and L in that order on an Epetra_MultiVector X in Y. More...

int	Condest (bool Trans, double &ConditionNumberEstimate) const
	Returns the maximum over all the condition number estimate for each local ILU set of factors. More...

double	GetRelaxValue ()
	Get RILU(k) relaxation parameter. More...

double	GetAbsoluteThreshold ()
	Get absolute threshold value. More...

double	GetRelativeThreshold ()
	Get relative threshold value. More...

Epetra_CombineMode	GetOverlapMode ()
	Get overlap mode type. More...

int	NumGlobalRows () const
	Returns the number of global matrix rows. More...

int	NumGlobalCols () const
	Returns the number of global matrix columns. More...

int	NumGlobalNonzeros () const
	Returns the number of nonzero entries in the global graph. More...

virtual int	NumGlobalBlockDiagonals () const
	Returns the number of diagonal entries found in the global input graph. More...

long long	NumGlobalRows64 () const

long long	NumGlobalCols64 () const

long long	NumGlobalNonzeros64 () const

virtual long long	NumGlobalBlockDiagonals64 () const

int	NumMyRows () const
	Returns the number of local matrix rows. More...

int	NumMyCols () const
	Returns the number of local matrix columns. More...

int	NumMyNonzeros () const
	Returns the number of nonzero entries in the local graph. More...

virtual int	NumMyBlockDiagonals () const
	Returns the number of diagonal entries found in the local input graph. More...

virtual int	NumMyDiagonals () const
	Returns the number of nonzero diagonal values found in matrix. More...

int	IndexBase () const
	Returns the index base for row and column indices for this graph. More...

long long	IndexBase64 () const

const Ifpack_IlukGraph &	Graph () const
	returns the address of the Ifpack_IlukGraph associated with this factored matrix. More...

const Epetra_CrsMatrix &	L () const
	Returns the address of the L factor associated with this factored matrix. More...

const Epetra_Vector &	D () const
	Returns the address of the D factor associated with this factored matrix. More...

const Epetra_CrsMatrix &	U () const
	Returns the address of the L factor associated with this factored matrix. More...

Protected Member Functions
void	SetFactored (bool Flag)

void	SetValuesInitialized (bool Flag)

bool	Allocated () const

int	SetAllocated (bool Flag)

int	BlockGraph2PointGraph (const Epetra_CrsGraph &BG, Epetra_CrsGraph &PG, bool Upper)

Private Member Functions
int	AllocateCrs ()

int	AllocateVbr ()

int	InitAllValues (const Epetra_RowMatrix &A, int MaxNumEntries)

int	BlockMap2PointMap (const Epetra_BlockMap &BlockMap, Teuchos::RefCountPtr< Epetra_Map > *PointMap)

int	GenerateXY (bool Trans, const Epetra_MultiVector &Xin, const Epetra_MultiVector &Yin, Teuchos::RefCountPtr< Epetra_MultiVector > Xout, Teuchos::RefCountPtr< Epetra_MultiVector > Yout) const

Private Attributes
bool	UserMatrixIsVbr_

bool	UserMatrixIsCrs_

bool	IsOverlapped_

const Ifpack_IlukGraph &	Graph_

Teuchos::RefCountPtr< Epetra_Map >	IlukRowMap_

Teuchos::RefCountPtr< Epetra_Map >	IlukDomainMap_

Teuchos::RefCountPtr< Epetra_Map >	IlukRangeMap_

Teuchos::RefCountPtr< const Epetra_Map >	U_DomainMap_

Teuchos::RefCountPtr< const Epetra_Map >	L_RangeMap_

const Epetra_Comm &	Comm_

Teuchos::RefCountPtr < Epetra_CrsMatrix >	L_

Teuchos::RefCountPtr < Epetra_CrsMatrix >	U_

Teuchos::RefCountPtr < Epetra_CrsGraph >	L_Graph_

Teuchos::RefCountPtr < Epetra_CrsGraph >	U_Graph_

Teuchos::RefCountPtr < Epetra_Vector >	D_

bool	UseTranspose_

int	NumMyDiagonals_

bool	Allocated_

bool	ValuesInitialized_

bool	Factored_

double	RelaxValue_

double	Athresh_

double	Rthresh_

double	Condest_

Teuchos::RefCountPtr < Epetra_MultiVector >	OverlapX_

Teuchos::RefCountPtr < Epetra_MultiVector >	OverlapY_

Teuchos::RefCountPtr < Epetra_MultiVector >	VbrX_

Teuchos::RefCountPtr < Epetra_MultiVector >	VbrY_

Epetra_CombineMode	OverlapMode_

Friends
std::ostream &	operator<< (std::ostream &os, const Ifpack_CrsRiluk &A)
	<< operator will work for Ifpack_CrsRiluk. More...

const char *	Label () const
	Returns a character string describing the operator. More...

int	SetUseTranspose (bool UseTranspose_in)
	If set true, transpose of this operator will be applied. More...

int	Apply (const Epetra_MultiVector &X, Epetra_MultiVector &Y) const
	Returns the result of a Epetra_Operator applied to a Epetra_MultiVector X in Y. More...

int	ApplyInverse (const Epetra_MultiVector &X, Epetra_MultiVector &Y) const
	Returns the result of a Epetra_Operator inverse applied to an Epetra_MultiVector X in Y. More...

double	NormInf () const
	Returns 0.0 because this class cannot compute Inf-norm. More...

bool	HasNormInf () const
	Returns false because this class cannot compute an Inf-norm. More...

bool	UseTranspose () const
	Returns the current UseTranspose setting. More...

const Epetra_Map &	OperatorDomainMap () const
	Returns the Epetra_Map object associated with the domain of this operator. More...

const Epetra_Map &	OperatorRangeMap () const
	Returns the Epetra_Map object associated with the range of this operator. More...

const Epetra_Comm &	Comm () const
	Returns the Epetra_BlockMap object associated with the range of this matrix operator. More...

Detailed Description

Ifpack_CrsRiluk: A class for constructing and using an incomplete lower/upper (ILU) factorization of a given Epetra_RowMatrix.

The Ifpack_CrsRiluk class computes a "Relaxed" ILU factorization with level k fill
of a given Epetra_CrsMatrix.  The factorization
that is produced is a function of several parameters:

The pattern of the matrix - All fill is derived from the original matrix nonzero structure. Level zero fill is defined as the original matrix pattern (nonzero structure), even if the matrix value at an entry is stored as a zero. (Thus it is possible to add entries to the ILU factors by adding zero entries the original matrix.)
Level of fill - Starting with the original matrix pattern as level fill of zero, the next level of fill is determined by analyzing the graph of the previous level and determining nonzero fill that is a result of combining entries that were from previous level only (not the current level). This rule limits fill to entries that are direct decendents from the previous level graph. Fill for level k is determined by applying this rule recursively. For sufficiently large values of k, the fill would eventually be complete and an exact LU factorization would be computed. Level of fill is defined during the construction of the Ifpack_IlukGraph object.
Level of overlap - All Ifpack preconditioners work on parallel distributed memory computers by using the row partitioning the user input matrix to determine the partitioning for local ILU factors. If the level of overlap is set to zero, the rows of the user matrix that are stored on a given processor are treated as a self-contained local matrix and all column entries that reach to off-processor entries are ignored. Setting the level of overlap to one tells Ifpack to increase the size of the local matrix by adding rows that are reached to by rows owned by this processor. Increasing levels of overlap are defined recursively in the same way. For sufficiently large levels of overlap, the entire matrix would be part of each processor's local ILU factorization process. Level of overlap is defined during the construction of the Ifpack_IlukGraph object.

Once the factorization is computed, applying the factorization (LUy = x) results in redundant approximations for any elements of y that correspond to rows that are part of more than one local ILU factor. The OverlapMode (changed by calling SetOverlapMode()) defines how these redundancies are handled using the Epetra_CombineMode enum. The default is to zero out all values of y for rows that were not part of the original matrix row distribution.
Fraction of relaxation - Ifpack_CrsRiluk computes the ILU factorization row-by-row. As entries at a given row are computed, some number of them will be dropped because they do match the prescribed sparsity pattern. The relaxation factor determines how these dropped values will be handled. If the RelaxValue (changed by calling SetRelaxValue()) is zero, then these extra entries will by dropped. This is a classical ILU approach. If the RelaxValue is 1, then the sum of the extra entries will be added to the diagonal. This is a classical Modified ILU (MILU) approach. If RelaxValue is between 0 and 1, then RelaxValue times the sum of extra entries will be added to the diagonal.

For most situations, RelaxValue should be set to zero. For certain kinds of problems, e.g., reservoir modeling, there is a conservation principle involved such that any operator should obey a zero row-sum property. MILU was designed for these cases and you should set the RelaxValue to 1. For other situations, setting RelaxValue to some nonzero value may improve the stability of factorization, and can be used if the computed ILU factors are poorly conditioned.
Diagonal perturbation - Prior to computing the factorization, it is possible to modify the diagonal entries of the matrix for which the factorization will be computing. If the absolute and relative perturbation values are zero and one, respectively, the factorization will be compute for the original user matrix A. Otherwise, the factorization will computed for a matrix that differs from the original user matrix in the diagonal values only. Below we discuss the details of diagonal perturbations. The absolute and relative threshold values are set by calling SetAbsoluteThreshold() and SetRelativeThreshold(), respectively.

Estimating Preconditioner Condition Numbers

For ill-conditioned matrices, we often have difficulty computing usable incomplete factorizations. The most common source of problems is that the factorization may encounter a small or zero pivot, in which case the factorization can fail, or even if the factorization succeeds, the factors may be so poorly conditioned that use of them in the iterative phase produces meaningless results. Before we can fix this problem, we must be able to detect it. To this end, we use a simple but effective condition number estimate for 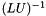$(LU)^{-1}$ .

The condition of a matrix 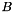$B$ , called 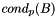$cond_p(B)$ , is defined as 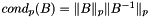$cond_p(B) = \|B\|_p\|B^{-1}\|_p$ in some appropriate norm 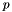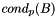$p$ . gives some indication of how many accurate floating point digits can be expected from operations involving the matrix and its inverse. 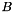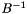A condition number approaching the accuracy of a given floating point number system, about 15 decimal digits in IEEE double precision, means that any results involving $B$ or $B^{-1}$ may be meaningless.

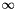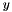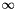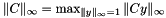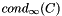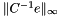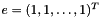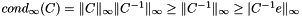The $\infty$ -norm of a vector $y$ is defined as the maximum of the absolute values of the vector entries, and the $\infty$ -norm of a matrix C is defined as $\|C\|_\infty = \max_{\|y\|_\infty = 1} \|Cy\|_\infty$ . A crude lower bound for the $cond_\infty(C)$ is $\|C^{-1}e\|_\infty$ where $e = (1, 1, \ldots, 1)^T$ . It is a lower bound because $cond_\infty(C) = \|C\|_\infty\|C^{-1}\|_\infty \ge \|C^{-1}\|_\infty \ge |C^{-1}e\|_\infty$ .

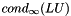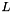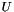For our purposes, we want to estimate $cond_\infty(LU)$ , where $L$ and $U$ are our incomplete factors. Edmond in his Ph.D. thesis demonstrates that 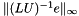$\|(LU)^{-1}e\|_\infty$ provides an effective estimate for 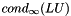$cond_\infty(LU)$ . 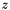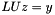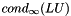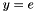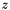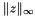Furthermore, since finding $z$ such that $LUz = y$ is a basic kernel for applying the preconditioner, computing this estimate of $cond_\infty(LU)$ is performed by setting $y = e$ , calling the solve kernel to compute $z$ and then computing $\|z\|_\infty$ .

A priori Diagonal Perturbations

Given the above method to estimate the conditioning of the incomplete factors, if we detect that our factorization is too ill-conditioned we can improve the conditioning by perturbing the matrix diagonal and restarting the factorization using this more diagonally dominant matrix. In order to apply perturbation, prior to starting the factorization, we compute a diagonal perturbation of our matrix 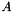$A$ and perform the factorization on this perturbed matrix. The overhead cost of perturbing the diagonal is minimal since the first step in computing the incomplete factors is to copy the matrix 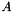$A$ into the memory space for the incomplete factors. We simply compute the perturbed diagonal at this point.

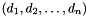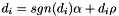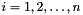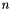The actual perturbation values we use are the diagonal values $(d_1, d_2, \ldots, d_n)$ with $d_i = sgn(d_i)\alpha + d_i\rho$ , $i=1, 2, \ldots, n$ , where $n$ is the matrix dimension and 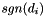$sgn(d_i)$ returns the sign of the diagonal entry. This has the effect of forcing the diagonal values to have minimal magnitude of 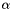$\alpha$ and to increase each by an amount proportional to 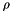$\rho$ , and still keep the sign of the original diagonal entry.

Constructing Ifpack_CrsRiluk objects

Constructing Ifpack_CrsRiluk objects is a multi-step process. The basic steps are as follows:

Create Ifpack_CrsRiluk instance, including storage, via constructor.
Enter values via one or more Put or SumInto functions.
Complete construction via FillComplete call.

Note that, even after a matrix is constructed, it is possible to update existing matrix entries. It is not possible to create new entries.

Counting Floating Point Operations

Each Ifpack_CrsRiluk object keep track of the number of serial floating point operations performed using the specified object as the this argument to the function. The Flops() function returns this number as a double precision number. Using this information, in conjunction with the Epetra_Time class, one can get accurate parallel performance numbers. The ResetFlops() function resets the floating point counter.

Warning: A Epetra_Map is required for the Ifpack_CrsRiluk constructor.

Definition at line 210 of file Ifpack_CrsRiluk.h.

Constructor & Destructor Documentation

Ifpack_CrsRiluk::Ifpack_CrsRiluk ( const Ifpack_IlukGraph & Graph_in )

Ifpack_CrsRiluk constuctor with variable number of indices per row.

Creates a Ifpack_CrsRiluk object and allocates storage.

Parameters

In	Graph_in - Graph generated by Ifpack_IlukGraph.

Definition at line 55 of file Ifpack_CrsRiluk.cpp.

Ifpack_CrsRiluk::Ifpack_CrsRiluk ( const Ifpack_CrsRiluk & Matrix )

Copy constructor.

Definition at line 76 of file Ifpack_CrsRiluk.cpp.

Ifpack_CrsRiluk::~Ifpack_CrsRiluk ( )

virtual

Ifpack_CrsRiluk Destructor.

Definition at line 105 of file Ifpack_CrsRiluk.cpp.

Member Function Documentation

int Ifpack_CrsRiluk::InitValues ( const Epetra_CrsMatrix & A )

Initialize L and U with values from user matrix A.

Copies values from the user's matrix into the nonzero pattern of L and U.

Parameters

In	A - User matrix to be factored.

Warning: The graph of A must be identical to the graph passed in to Ifpack_IlukGraph constructor.

Definition at line 182 of file Ifpack_CrsRiluk.cpp.

int Ifpack_CrsRiluk::InitValues ( const Epetra_VbrMatrix & A )

Initialize L and U with values from user matrix A.

Copies values from the user's matrix into the nonzero pattern of L and U.

Parameters

In	A - User matrix to be factored.

Warning: The graph of A must be identical to the graph passed in to Ifpack_IlukGraph constructor.

Definition at line 212 of file Ifpack_CrsRiluk.cpp.

bool Ifpack_CrsRiluk::ValuesInitialized ( ) const

inline

If values have been initialized, this query returns true, otherwise it returns false.

Definition at line 252 of file Ifpack_CrsRiluk.h.

void Ifpack_CrsRiluk::SetRelaxValue ( double RelaxValue )

inline

Set RILU(k) relaxation parameter.

Definition at line 255 of file Ifpack_CrsRiluk.h.

void Ifpack_CrsRiluk::SetAbsoluteThreshold ( double Athresh )

inline

Set absolute threshold value.

Definition at line 258 of file Ifpack_CrsRiluk.h.

void Ifpack_CrsRiluk::SetRelativeThreshold ( double Rthresh )

inline

Set relative threshold value.

Definition at line 261 of file Ifpack_CrsRiluk.h.

void Ifpack_CrsRiluk::SetOverlapMode ( Epetra_CombineMode OverlapMode )

inline

Set overlap mode type.

Definition at line 264 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::SetParameters	(	const Teuchos::ParameterList &	parameterlist,
		bool	cerr_warning_if_unused = `false`
	)

Set parameters using a Teuchos::ParameterList object.

Definition at line 162 of file Ifpack_CrsRiluk.cpp.

int Ifpack_CrsRiluk::Factor ( void )

Compute ILU factors L and U using the specified graph, diagonal perturbation thresholds and relaxation parameters.

This function computes the RILU(k) factors L and U using the current:

Ifpack_IlukGraph specifying the structure of L and U.
Value for the RILU(k) relaxation parameter.
Value for the a priori diagonal threshold values.

InitValues() must be called before the factorization can proceed.

Definition at line 361 of file Ifpack_CrsRiluk.cpp.

bool Ifpack_CrsRiluk::Factored ( ) const

inline

If factor is completed, this query returns true, otherwise it returns false.

Definition at line 289 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::Solve	(	bool	Trans,
		const Epetra_MultiVector &	X,
		Epetra_MultiVector &	Y
	)		const

Returns the result of a Ifpack_CrsRiluk forward/back solve on a Epetra_MultiVector X in Y (works for Epetra_Vectors also).

Parameters

In	Trans -If true, solve transpose problem.
In	X - A Epetra_MultiVector of dimension NumVectors to solve for.
Out	Y -A Epetra_MultiVector of dimension NumVectorscontaining result.

Returns: Integer error code, set to 0 if successful.

Definition at line 513 of file Ifpack_CrsRiluk.cpp.

int Ifpack_CrsRiluk::Multiply	(	bool	Trans,
		const Epetra_MultiVector &	X,
		Epetra_MultiVector &	Y
	)		const

Returns the result of multiplying U, D and L in that order on an Epetra_MultiVector X in Y.

Parameters

In	Trans -If true, multiply by L^T, D and U^T in that order.
In	X - A Epetra_MultiVector of dimension NumVectors to solve for.
Out	Y -A Epetra_MultiVector of dimension NumVectorscontaining result.

Returns: Integer error code, set to 0 if successful.

Definition at line 554 of file Ifpack_CrsRiluk.cpp.

int Ifpack_CrsRiluk::Condest	(	bool	Trans,
		double &	ConditionNumberEstimate
	)		const

Returns the maximum over all the condition number estimate for each local ILU set of factors.

This functions computes a local condition number estimate on each processor and return the maximum over all processor of the estimate.

Parameters

In	Trans -If true, solve transpose problem.
Out	ConditionNumberEstimate - The maximum across all processors of the infinity-norm estimate of the condition number of the inverse of LDU.

Definition at line 596 of file Ifpack_CrsRiluk.cpp.

double Ifpack_CrsRiluk::GetRelaxValue ( )

inline

Get RILU(k) relaxation parameter.

Definition at line 334 of file Ifpack_CrsRiluk.h.

double Ifpack_CrsRiluk::GetAbsoluteThreshold ( )

inline

Get absolute threshold value.

Definition at line 337 of file Ifpack_CrsRiluk.h.

double Ifpack_CrsRiluk::GetRelativeThreshold ( )

inline

Get relative threshold value.

Definition at line 340 of file Ifpack_CrsRiluk.h.

Epetra_CombineMode Ifpack_CrsRiluk::GetOverlapMode ( )

inline

Get overlap mode type.

Definition at line 343 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::NumGlobalRows ( ) const

inline

Returns the number of global matrix rows.

Definition at line 348 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::NumGlobalCols ( ) const

inline

Returns the number of global matrix columns.

Definition at line 351 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::NumGlobalNonzeros ( ) const

inline

Returns the number of nonzero entries in the global graph.

Definition at line 354 of file Ifpack_CrsRiluk.h.

virtual int Ifpack_CrsRiluk::NumGlobalBlockDiagonals ( ) const

inlinevirtual

Returns the number of diagonal entries found in the global input graph.

Definition at line 357 of file Ifpack_CrsRiluk.h.

long long Ifpack_CrsRiluk::NumGlobalRows64 ( ) const

inline

Definition at line 360 of file Ifpack_CrsRiluk.h.

long long Ifpack_CrsRiluk::NumGlobalCols64 ( ) const

inline

Definition at line 361 of file Ifpack_CrsRiluk.h.

long long Ifpack_CrsRiluk::NumGlobalNonzeros64 ( ) const

inline

Definition at line 362 of file Ifpack_CrsRiluk.h.

virtual long long Ifpack_CrsRiluk::NumGlobalBlockDiagonals64 ( ) const

inlinevirtual

Definition at line 363 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::NumMyRows ( ) const

inline

Returns the number of local matrix rows.

Definition at line 366 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::NumMyCols ( ) const

inline

Returns the number of local matrix columns.

Definition at line 369 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::NumMyNonzeros ( ) const

inline

Returns the number of nonzero entries in the local graph.

Definition at line 372 of file Ifpack_CrsRiluk.h.

virtual int Ifpack_CrsRiluk::NumMyBlockDiagonals ( ) const

inlinevirtual

Returns the number of diagonal entries found in the local input graph.

Definition at line 375 of file Ifpack_CrsRiluk.h.

virtual int Ifpack_CrsRiluk::NumMyDiagonals ( ) const

inlinevirtual

Returns the number of nonzero diagonal values found in matrix.

Definition at line 378 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::IndexBase ( ) const

inline

Returns the index base for row and column indices for this graph.

Definition at line 382 of file Ifpack_CrsRiluk.h.

long long Ifpack_CrsRiluk::IndexBase64 ( ) const

inline

Definition at line 384 of file Ifpack_CrsRiluk.h.

const Ifpack_IlukGraph& Ifpack_CrsRiluk::Graph ( ) const

inline

returns the address of the Ifpack_IlukGraph associated with this factored matrix.

Definition at line 387 of file Ifpack_CrsRiluk.h.

const Epetra_CrsMatrix& Ifpack_CrsRiluk::L ( ) const

inline

Returns the address of the L factor associated with this factored matrix.

Definition at line 390 of file Ifpack_CrsRiluk.h.

const Epetra_Vector& Ifpack_CrsRiluk::D ( ) const

inline

Returns the address of the D factor associated with this factored matrix.

Definition at line 393 of file Ifpack_CrsRiluk.h.

const Epetra_CrsMatrix& Ifpack_CrsRiluk::U ( ) const

inline

Returns the address of the L factor associated with this factored matrix.

Definition at line 396 of file Ifpack_CrsRiluk.h.

const char* Ifpack_CrsRiluk::Label ( ) const

inlinevirtual

Returns a character string describing the operator.

Implements Epetra_Operator.

Definition at line 401 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::SetUseTranspose ( bool UseTranspose_in )

inlinevirtual

If set true, transpose of this operator will be applied.

This flag allows the transpose of the given operator to be used implicitly.  Setting this flag
affects only the Apply() and ApplyInverse() methods.  If the implementation of this interface
does not support transpose use, this method should return a value of -1.

Parameters

In	UseTranspose_in -If true, multiply by the transpose of operator, otherwise just use operator.

Returns: Always returns 0.

Implements Epetra_Operator.

Definition at line 413 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::Apply	(	const Epetra_MultiVector &	X,
		Epetra_MultiVector &	Y
	)		const

inlinevirtual

Returns the result of a Epetra_Operator applied to a Epetra_MultiVector X in Y.

Note that this implementation of Apply does NOT perform a forward back solve with
the LDU factorization.  Instead it applies these operators via multiplication with
U, D and L respectively.  The ApplyInverse() method performs a solve.

Parameters

In	X - A Epetra_MultiVector of dimension NumVectors to multiply with matrix.
Out	Y -A Epetra_MultiVector of dimension NumVectors containing result.

Returns: Integer error code, set to 0 if successful.

Implements Epetra_Operator.

Definition at line 427 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::ApplyInverse	(	const Epetra_MultiVector &	X,
		Epetra_MultiVector &	Y
	)		const

inlinevirtual

Returns the result of a Epetra_Operator inverse applied to an Epetra_MultiVector X in Y.

In this implementation, we use several existing attributes to determine how virtual
method ApplyInverse() should call the concrete method Solve().  We pass in the UpperTriangular(),
the Epetra_CrsMatrix::UseTranspose(), and NoDiagonal() methods. The most notable warning is that
if a matrix has no diagonal values we assume that there is an implicit unit diagonal that should
be accounted for when doing a triangular solve.

Parameters

In	X - A Epetra_MultiVector of dimension NumVectors to solve for.
Out	Y -A Epetra_MultiVector of dimension NumVectors containing result.

Returns: Integer error code, set to 0 if successful.

Implements Epetra_Operator.

Definition at line 444 of file Ifpack_CrsRiluk.h.

double Ifpack_CrsRiluk::NormInf ( ) const

inlinevirtual

Returns 0.0 because this class cannot compute Inf-norm.

Implements Epetra_Operator.

Definition at line 448 of file Ifpack_CrsRiluk.h.

bool Ifpack_CrsRiluk::HasNormInf ( ) const

inlinevirtual

Returns false because this class cannot compute an Inf-norm.

Implements Epetra_Operator.

Definition at line 451 of file Ifpack_CrsRiluk.h.

bool Ifpack_CrsRiluk::UseTranspose ( ) const

inlinevirtual

Returns the current UseTranspose setting.

Implements Epetra_Operator.

Definition at line 454 of file Ifpack_CrsRiluk.h.

const Epetra_Map& Ifpack_CrsRiluk::OperatorDomainMap ( ) const

inlinevirtual

Returns the Epetra_Map object associated with the domain of this operator.

Implements Epetra_Operator.

Definition at line 457 of file Ifpack_CrsRiluk.h.

const Epetra_Map& Ifpack_CrsRiluk::OperatorRangeMap ( ) const

inlinevirtual

Returns the Epetra_Map object associated with the range of this operator.

Implements Epetra_Operator.

Definition at line 460 of file Ifpack_CrsRiluk.h.

const Epetra_Comm& Ifpack_CrsRiluk::Comm ( ) const

inlinevirtual

Returns the Epetra_BlockMap object associated with the range of this matrix operator.

Implements Epetra_Operator.

Definition at line 463 of file Ifpack_CrsRiluk.h.

void Ifpack_CrsRiluk::SetFactored ( bool Flag )

inlineprotected

Definition at line 467 of file Ifpack_CrsRiluk.h.

void Ifpack_CrsRiluk::SetValuesInitialized ( bool Flag )

inlineprotected

Definition at line 468 of file Ifpack_CrsRiluk.h.

bool Ifpack_CrsRiluk::Allocated ( ) const

inlineprotected

Definition at line 469 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::SetAllocated ( bool Flag )

inlineprotected

Definition at line 470 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::BlockGraph2PointGraph	(	const Epetra_CrsGraph &	BG,
		Epetra_CrsGraph &	PG,
		bool	Upper
	)

protected

Definition at line 614 of file Ifpack_CrsRiluk.cpp.

int Ifpack_CrsRiluk::AllocateCrs ( )

private

Definition at line 112 of file Ifpack_CrsRiluk.cpp.

int Ifpack_CrsRiluk::AllocateVbr ( )

private

Definition at line 124 of file Ifpack_CrsRiluk.cpp.

int Ifpack_CrsRiluk::InitAllValues	(	const Epetra_RowMatrix &	A,
		int	MaxNumEntries
	)

private

Definition at line 251 of file Ifpack_CrsRiluk.cpp.

int Ifpack_CrsRiluk::BlockMap2PointMap	(	const Epetra_BlockMap &	BlockMap,
		Teuchos::RefCountPtr< Epetra_Map > *	PointMap
	)

private

Definition at line 675 of file Ifpack_CrsRiluk.cpp.

int Ifpack_CrsRiluk::GenerateXY	(	bool	Trans,
		const Epetra_MultiVector &	Xin,
		const Epetra_MultiVector &	Yin,
		Teuchos::RefCountPtr< Epetra_MultiVector > *	Xout,
		Teuchos::RefCountPtr< Epetra_MultiVector > *	Yout
	)		const

private

Definition at line 734 of file Ifpack_CrsRiluk.cpp.

Friends And Related Function Documentation

std::ostream& operator<<	(	std::ostream &	os,
		const Ifpack_CrsRiluk &	A
	)

friend

<< operator will work for Ifpack_CrsRiluk.

Definition at line 795 of file Ifpack_CrsRiluk.cpp.

Member Data Documentation

bool Ifpack_CrsRiluk::UserMatrixIsVbr_

private

Definition at line 484 of file Ifpack_CrsRiluk.h.

bool Ifpack_CrsRiluk::UserMatrixIsCrs_

private

Definition at line 485 of file Ifpack_CrsRiluk.h.

bool Ifpack_CrsRiluk::IsOverlapped_

private

Definition at line 486 of file Ifpack_CrsRiluk.h.

const Ifpack_IlukGraph& Ifpack_CrsRiluk::Graph_

private

Definition at line 487 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<Epetra_Map> Ifpack_CrsRiluk::IlukRowMap_

private

Definition at line 488 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<Epetra_Map> Ifpack_CrsRiluk::IlukDomainMap_

private

Definition at line 489 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<Epetra_Map> Ifpack_CrsRiluk::IlukRangeMap_

private

Definition at line 490 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<const Epetra_Map> Ifpack_CrsRiluk::U_DomainMap_

private

Definition at line 491 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<const Epetra_Map> Ifpack_CrsRiluk::L_RangeMap_

private

Definition at line 492 of file Ifpack_CrsRiluk.h.

const Epetra_Comm& Ifpack_CrsRiluk::Comm_

private

Definition at line 493 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<Epetra_CrsMatrix> Ifpack_CrsRiluk::L_

private

Definition at line 494 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<Epetra_CrsMatrix> Ifpack_CrsRiluk::U_

private

Definition at line 495 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<Epetra_CrsGraph> Ifpack_CrsRiluk::L_Graph_

private

Definition at line 496 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<Epetra_CrsGraph> Ifpack_CrsRiluk::U_Graph_

private

Definition at line 497 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<Epetra_Vector> Ifpack_CrsRiluk::D_

private

Definition at line 498 of file Ifpack_CrsRiluk.h.

bool Ifpack_CrsRiluk::UseTranspose_

private

Definition at line 499 of file Ifpack_CrsRiluk.h.

int Ifpack_CrsRiluk::NumMyDiagonals_

private

Definition at line 501 of file Ifpack_CrsRiluk.h.

bool Ifpack_CrsRiluk::Allocated_

private

Definition at line 502 of file Ifpack_CrsRiluk.h.

bool Ifpack_CrsRiluk::ValuesInitialized_

private

Definition at line 503 of file Ifpack_CrsRiluk.h.

bool Ifpack_CrsRiluk::Factored_

private

Definition at line 504 of file Ifpack_CrsRiluk.h.

double Ifpack_CrsRiluk::RelaxValue_

private

Definition at line 505 of file Ifpack_CrsRiluk.h.

double Ifpack_CrsRiluk::Athresh_

private

Definition at line 506 of file Ifpack_CrsRiluk.h.

double Ifpack_CrsRiluk::Rthresh_

private

Definition at line 507 of file Ifpack_CrsRiluk.h.

double Ifpack_CrsRiluk::Condest_

mutableprivate

Definition at line 508 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<Epetra_MultiVector> Ifpack_CrsRiluk::OverlapX_

mutableprivate

Definition at line 510 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<Epetra_MultiVector> Ifpack_CrsRiluk::OverlapY_

mutableprivate

Definition at line 511 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<Epetra_MultiVector> Ifpack_CrsRiluk::VbrX_

mutableprivate

Definition at line 512 of file Ifpack_CrsRiluk.h.

Teuchos::RefCountPtr<Epetra_MultiVector> Ifpack_CrsRiluk::VbrY_

mutableprivate

Definition at line 513 of file Ifpack_CrsRiluk.h.

Epetra_CombineMode Ifpack_CrsRiluk::OverlapMode_

private

Definition at line 514 of file Ifpack_CrsRiluk.h.

The documentation for this class was generated from the following files:

Public Member Functions

Protected Member Functions

Private Member Functions

Private Attributes

Friends

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

Member Data Documentation