This class implements a TraceMIN iteration, a preconditioned iteration for solving linear symmetric positive definite eigenproblems. More...

#include <AnasaziTraceMin.hpp>

Inheritance diagram for Anasazi::Experimental::TraceMin< ScalarType, MV, OP >:

Constructor/Destructor
	TraceMin (const Teuchos::RCP< Eigenproblem< ScalarType, MV, OP > > &problem, const Teuchos::RCP< SortManager< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > > &sorter, const Teuchos::RCP< OutputManager< ScalarType > > &printer, const Teuchos::RCP< StatusTest< ScalarType, MV, OP > > &tester, const Teuchos::RCP< MatOrthoManager< ScalarType, MV, OP > > &ortho, Teuchos::ParameterList &params)
	TraceMin constructor with eigenproblem, solver utilities, and parameter list of solver options. More...

Additional Inherited Members
Public Member Functions inherited from Anasazi::Experimental::TraceMinBase< ScalarType, MV, OP >
	TraceMinBase (const RCP< Eigenproblem< ScalarType, MV, OP > > &problem, const RCP< SortManager< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > > &sorter, const RCP< OutputManager< ScalarType > > &printer, const RCP< StatusTest< ScalarType, MV, OP > > &tester, const RCP< MatOrthoManager< ScalarType, MV, OP > > &ortho, Teuchos::ParameterList &params)
	TraceMinBase constructor with eigenproblem, solver utilities, and parameter list of solver options. More...

virtual	~TraceMinBase ()
	Anasazi::TraceMinBase destructor. More...

void	iterate ()
	This method performs trace minimization iterations until the status test indicates the need to stop or an error occurs (in which case, an appropriate exception is thrown). More...

void	harmonicIterate ()

void	initialize (TraceMinBaseState< ScalarType, MV > &newstate)
	Initialize the solver to an iterate, optionally providing the other members of the state. More...

void	harmonicInitialize (TraceMinBaseState< ScalarType, MV > newstate)

void	initialize ()
	Initialize the solver with the initial vectors from the eigenproblem or random data. More...

bool	isInitialized () const
	Indicates whether the solver has been initialized or not. More...

TraceMinBaseState< ScalarType, MV >	getState () const
	Get access to the current state of the eigensolver. More...

int	getNumIters () const
	Get the current iteration count. More...

void	resetNumIters ()
	Reset the iteration count. More...

RCP< const MV >	getRitzVectors ()
	Get access to the current Ritz vectors. More...

std::vector< Value< ScalarType > >	getRitzValues ()
	Get the Ritz values for the previous iteration. More...

std::vector< int >	getRitzIndex ()
	Get the index used for extracting individual Ritz vectors from getRitzVectors(). More...

std::vector< typename Teuchos::ScalarTraits < ScalarType >::magnitudeType >	getResNorms ()
	Get the current residual norms, computing the norms if they are not up-to-date with the current residual vectors. More...

std::vector< typename Teuchos::ScalarTraits < ScalarType >::magnitudeType >	getRes2Norms ()
	Get the current residual 2-norms, computing the norms if they are not up-to-date with the current residual vectors. More...

std::vector< typename Teuchos::ScalarTraits < ScalarType >::magnitudeType >	getRitzRes2Norms ()
	Get the 2-norms of the residuals. More...

int	getCurSubspaceDim () const
	Get the dimension of the search subspace used to generate the current eigenvectors and eigenvalues. More...

int	getMaxSubspaceDim () const
	Get the maximum dimension allocated for the search subspace. For the trace minimization methods, this always returns numBlocks*blockSize. More...

void	setStatusTest (RCP< StatusTest< ScalarType, MV, OP > > test)
	Set a new StatusTest for the solver. More...

RCP< StatusTest< ScalarType, MV, OP > >	getStatusTest () const
	Get the current StatusTest used by the solver. More...

const Eigenproblem< ScalarType, MV, OP > &	getProblem () const
	Get a constant reference to the eigenvalue problem. More...

void	setBlockSize (int blockSize)
	Set the blocksize. More...

int	getBlockSize () const
	Get the blocksize used by the iterative solver. More...

void	setAuxVecs (const Teuchos::Array< RCP< const MV > > &auxvecs)
	Set the auxiliary vectors for the solver. More...

Teuchos::Array< RCP< const MV > >	getAuxVecs () const
	Get the auxiliary vectors for the solver. More...

void	setSize (int blockSize, int numBlocks)
	Set the blocksize and number of blocks to be used by the iterative solver in solving this eigenproblem. More...

void	currentStatus (std::ostream &os)
	This method requests that the solver print out its current status to the given output stream. More...

Public Member Functions inherited from Anasazi::Eigensolver< ScalarType, MV, OP >
	Eigensolver ()
	Default Constructor. More...

	Eigensolver (const Teuchos::RCP< Eigenproblem< ScalarType, MV, OP > > &problem, const Teuchos::RCP< SortManager< ScalarType > > &sorter, const Teuchos::RCP< OutputManager< ScalarType > > &printer, const Teuchos::RCP< StatusTest< ScalarType, MV, OP > > &tester, const Teuchos::RCP< OrthoManager< ScalarType, MV > > &ortho, Teuchos::ParameterList &params)
	Basic Constructor. More...

virtual	~Eigensolver ()
	Destructor. More...

Detailed Description

template<class ScalarType, class MV, class OP>
class Anasazi::Experimental::TraceMin< ScalarType, MV, OP >

This class implements a TraceMIN iteration, a preconditioned iteration for solving linear symmetric positive definite eigenproblems.

TraceMin works by solving a constrained minimization problem

$\textrm{min trace}\left(Y^TKY\right) \textrm{ such that } Y^TMY = I$

The Y which satisfies this problem is the set of eigenvectors corresponding to the eigenvalues of smallest magnitude. While TraceMin is capable of finding any eigenpairs of 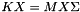$KX = MX \Sigma$ (where K is symmetric and M symmetric positive definite), it converges to the eigenvalues of smallest magnitude of whatever it is given. If a different set of eigenpairs is desired (such as the absolute smallest or the ones closest to a given shift), please perform a spectral transformation before passing the Eigenproblem to the solver.

A TraceMin iteration consists of the following operations:

Solve the saddle point problem
$\left[\begin{array}{lr} K & MX \\ X^TM & 0\end{array}\right] \left[\begin{array}{l} V \\ \tilde{L}\end{array}\right] = \left[\begin{array}{l} 0 \\ I\end{array}\right]$
Form 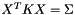a section out of the current subspace V such that $X^TKX = \Sigma$ and 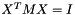, where 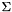$\Sigma$ is diagonal. 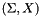$\left(\Sigma,X\right)$ is an approximation of the eigenpairs of smallest magnitude.
Compute the new residual and check for convergence.

The saddle point problem need not be solved to a low relative residual and can be solved either by directly forming the Schur complement or by using a projected Krylov subspace method to solve

$\left(PKP\right) \Delta = PMX \textrm{ with } P=I-BX\left(X^TB^2X\right)^{-1}X^TB$

Then V is constructed as 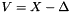$V=X-\Delta$ . If a preconditioner H is used with the projected Krylov method, it is applied as

$F=\left[I-H^{-1}BX\left(X^TBH^{-1}BX\right)^{-1}X^TB\right]H^{-1}$

and we solve 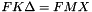$FK\Delta = FMX$ . (See A Parallel Implementation of the Trace Minimization Eigensolver by Eloy Romero and Jose E. Roman.)

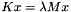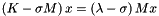The convergence rate of TraceMin is based on the distribution of eigenvalues. If the eigenvalues are clustered far away from the origin, we have a slow rate of convergence. We can improve our convergence rate by taking advantage of Ritz shifts. Instead of solving $Kx=\lambda Mx$ , we solve $\left(K-\sigma M\right) x = \left(\lambda - \sigma\right)Mx$ .

This method is described in A Trace Minimization Algorithm for the Generalized Eigenvalue Problem, Ahmed H. Sameh, John A. Wisniewski, SIAM Journal on Numerical Analysis, 19(6), pp. 1243-1259 (1982)

Author: Alicia Klinvex

Definition at line 131 of file AnasaziTraceMin.hpp.

Constructor & Destructor Documentation

template<class ScalarType , class MV , class OP >

Anasazi::Experimental::TraceMin< ScalarType, MV, OP >::TraceMin	(	const Teuchos::RCP< Eigenproblem< ScalarType, MV, OP > > &	problem,
		const Teuchos::RCP< SortManager< typename Teuchos::ScalarTraits< ScalarType >::magnitudeType > > &	sorter,
		const Teuchos::RCP< OutputManager< ScalarType > > &	printer,
		const Teuchos::RCP< StatusTest< ScalarType, MV, OP > > &	tester,
		const Teuchos::RCP< MatOrthoManager< ScalarType, MV, OP > > &	ortho,
		Teuchos::ParameterList &	params
	)

TraceMin constructor with eigenproblem, solver utilities, and parameter list of solver options.

This constructor takes pointers required by the eigensolver, in addition to a parameter list of options for the eigensolver. These options include the following:

"Block Size" - an int specifying the subspace dimension used by the algorithm. This can also be specified using the setBlockSize() method.
"Maximum Iterations" - an int specifying the maximum number of TraceMin iterations.
"Saddle Solver Type" - a string specifying the algorithm to use in solving the saddle point problem: "Schur Complement" or "Projected Krylov". Default: "Projected Krylov"
- "Schur Complement": We explicitly form the Schur complement and use it to solve the linear system. This option may be faster, but it is less numerically stable and does not ensure orthogonality between the current iterate and the update.
- "Projected Krylov": Use a projected iterative method to solve the linear system. If TraceMin was not given a preconditioner, it will use MINRES. Otherwise, it will use GMRES.
"Shift Type" - a string specifying how to choose Ritz shifts: "No Shift", "Locked Shift", "Trace Leveled Shift", or "Original Shift". Default: "Trace Leveled Shift"
- "No Shift": Do not perform Ritz shifts. This option produces guaranteed convergence but converges linearly. Not recommended.
- "Locked Shift": Do not perform Ritz shifts until an eigenpair is locked. Then, shift based on the largest converged eigenvalue. This option is roughly as safe as "No Shift" but may be faster.
- "Trace Leveled Shift": Do not perform Ritz shifts until the trace of 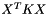(i.e. the quantity being minimized has stagnated. Then, shift based on the strategy proposed in The trace minimization method for the symmetric generalized eigenvalue problem. Highly recommended.
- "Original Shift": The original shifting strategy proposed in "The trace minimization method for the symmetric generalized eigenvalue problem." Compute shifts based on the Ritz values, residuals, and clustering of the eigenvalues. May produce incorrect results for indefinite matrices or small subspace dimensions.

Definition at line 215 of file AnasaziTraceMin.hpp.

The documentation for this class was generated from the following file:

AnasaziTraceMin.hpp

Constructor/Destructor

Additional Inherited Members

Detailed Description

template<class ScalarType, class MV, class OP> class Anasazi::Experimental::TraceMin< ScalarType, MV, OP >

Constructor & Destructor Documentation

template<class ScalarType, class MV, class OP>
class Anasazi::Experimental::TraceMin< ScalarType, MV, OP >