|
Teuchos - Trilinos Tools Package
Version of the Day
|
|
Teuchos - Trilinos Tools Package
Version of the Day
|
Interface for a method for solving linear system(s) AX=B. More...
#include <Trilinos_Details_LinearSolver.hpp>
Public Member Functions | |
| virtual | ~LinearSolver () |
| Destructor (virtual for memory safety of derived classes). More... | |
| virtual void | setMatrix (const Teuchos::RCP< const OP > &A)=0 |
| Set the solver's matrix. More... | |
| virtual Teuchos::RCP< const OP > | getMatrix () const =0 |
| Get a pointer to this solver's matrix. More... | |
| virtual void | solve (MV &X, const MV &B)=0 |
| Solve the linear system(s) AX=B. More... | |
| virtual void | setParameters (const Teuchos::RCP< Teuchos::ParameterList > ¶ms)=0 |
| Set this solver's parameters. More... | |
| virtual void | symbolic ()=0 |
| Set up any part of the solve that depends on the structure of the input matrix, but not its numerical values. More... | |
| virtual void | numeric ()=0 |
| Set up any part of the solve that depends on both the structure and the numerical values of the input matrix. More... | |
Interface for a method for solving linear system(s) AX=B.
| MV | Type of a (multi)vector, representing either the solution(s) X or the right-hand side(s) B of a linear system AX=B. For example, with Tpetra, use a Tpetra::MultiVector specialization. A multivector is a single data structure containing zero or more vectors with the same dimensions and layout. |
| OP | Type of a matrix or linear operator that this LinearSolver understands. For example, for Tpetra, use a Tpetra::Operator specialization. |
| NormType | Type of the norm of a vector (see MV); in particular, the type of the norm of a residual 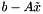 , where , where 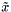 is an approximate solution of the linear system is an approximate solution of the linear system 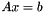 . For . For MV = Tpetra::MultiVector, use NormType = MV::mag_type. In general, if the entries of MV have type double, and the solver uses the Euclidean norm (i.e., the 2-norm), then NormType = double. If the entries of MV have type std::complex<float>, then NormType = float. |
A LinearSolver knows how to solve linear systems AX=B, where A is a linear operator ("matrix") and B the right-hand side(s).
This interface separates "setup" from "solves." "Setup" depends only on the matrix A, while solves also depend on the right-hand side(s) B and possibly also on initial guess(es). "Setup" may be more expensive than solve, but it can be reused for different right-hand side(s) and initial guess(es). The LinearSolver interface further divides setup into two phases: "symbolic" and "numeric."
The "symbolic" phase depends only on the "structure" of the matrix, and not its values. By "structure," we mean
The distinction between "structure" and "values" matters most for sparse matrices. If the structure of a matrix does not change, LinearSolver can reuse the "symbolic" setup phase for multiple solves, even if the values in the matrix change between solves. If the structure of a matrix changes, you must ask LinearSolver to recompute the symbolic setup.
The "numeric" setup phase depends on both the matrix's structure, and the values of its entries. If the values in the matrix change, you must ask the solver to recompute the numeric setup. If only the values changed but not the matrix's structure, then you do not need to ask the solver to recompute the symbolic setup. The symbolic setup must be done before the numeric setup.
OP template parameter, you should consistently use the most abstract base class that makes sense. For example, with Tpetra, use Tpetra::Operator, and for Epetra, use Epetra_Operator. Implementations should use dynamic_cast to get the subclass that they want, and throw an exception if the dynamic_cast fails. I emphasized "consistently," because this makes explicit template instantiation (ETI) easier, and helps keep build times and library sizes small. Definition at line 114 of file Trilinos_Details_LinearSolver.hpp.
|
inlinevirtual |
Destructor (virtual for memory safety of derived classes).
Definition at line 117 of file Trilinos_Details_LinearSolver.hpp.
|
pure virtual |
Set the solver's matrix.
| A | [in] Pointer to the matrix A in the linear system(s) AX=B to solve. |
This LinearSolver instance keeps the matrix (by pointer) given to it by this method, and does not modify it. The solver stores any additional data needed for solves separately from the matrix.
Calling this method resets the solver's state. After calling this method, you must call symbolic() and numeric() before you may call solve().
You are allowed to change the structure and/or numerical values in the matrix that this LinearSolver instance holds. If you do so, you do NOT need to call this method. If you change the graph structure of the matrix, you must call symbolic() and numeric() before you may call solve(). If you change the numerical values but not the graph structure of the matrix, you must call numeric() before you may call solve().
Teuchos::RCP is just like std::shared_ptr. It uses reference counting for automatic deallocation. Passing in a "const OP" implies that the solver may not modify A.
|
pure virtual |
Get a pointer to this solver's matrix.
If this LinearSolver instance does not (yet) have a matrix, this method will return Teuchos::null. The solver must have a matrix before you may call solve().
Teuchos::RCP is just like std::shared_ptr. It uses reference counting for automatic deallocation. Returning a "const OP" implies that the caller may not modify A.
|
pure virtual |
Solve the linear system(s) AX=B.
| X | [in/out] On input: (multi)vector that is allocated and ready for output. The solver may choose to read the contents as the initial guess(es). On output: the solution vector(s). |
| B | [in] Right-hand side(s) of the linear system(s). |
Solves may fail. "Failure" depends on the accuracy that the specific solver promises. The caller is responsible for determining whether the solve succeeded. This may require a dynamic cast to ask the specific kind of solver whether it succeeded, or testing some error metric (like the the residual 2-norm).
|
pure virtual |
Set this solver's parameters.
Depending on the solver and which parameters you set or changed, you may have to recompute the symbolic or numeric setup (by calling symbolic() resp. numeric()) after calling setParameters(), before you may call solve() again.
Different solver implementations have different ideas about how to treat parameters. Some of them (like those in Ifpack2) treat the input parameter list as a complete snapshot of the desired state. Many that do this also fill the input list with unspecified parameters set to default values. Other solvers (like those in Belos) treat the input list as a "delta" – a set of changes from the current state – and thus generally do not fill in the input list.
This interface is compatible with either variant. The solver reserves the right to modify the input list, or to keep a pointer to the input list. Callers are responsible for copying the list if they don't want the solver to see changes, or if the Teuchos::RCP is nonowning. Users are responsible for knowing how the different solvers behave.
|
pure virtual |
Set up any part of the solve that depends on the structure of the input matrix, but not its numerical values.
If the structure of the matrix has changed, or if you have not yet called this method on this LinearSolver instance, then you must call this method before you may call numeric() or solve().
There is no way that the solver can tell users whether the symbolic factorization is "done," because the solver may have no way to know whether the structure of the matrix has changed. Users are responsible for notifying the solver of structure changes, by calling symbolic(). (This is why there is no "symbolicDone" Boolean method.)
|
pure virtual |
Set up any part of the solve that depends on both the structure and the numerical values of the input matrix.
If any values in the matrix have changed, or if you have not yet called this method on this LinearSolver instance, then you must call this method before you may call solve().
There is no way that the solver can tell users whether the numeric factorization is "done," because the solver may have no way to know whether the values of the matrix has changed. Users are responsible for notifying the solver of changes to values, by calling numeric(). (This is why there is no "numericDone" Boolean method.)
 1.8.5
1.8.5