|
Stokhos
Development
|
|
Stokhos
Development
|
Generate a basis from a given set of PCE expansions that is orthogonal with respect to the product measure induced by these expansions. More...
#include <Stokhos_MonomialProjGramSchmidtPCEBasis2.hpp>
Public Member Functions | |
| MonomialProjGramSchmidtPCEBasis2 (ordinal_type p, const Teuchos::Array< Stokhos::OrthogPolyApprox< ordinal_type, value_type > > &pce, const Teuchos::RCP< const Stokhos::Quadrature< ordinal_type, value_type > > &quad, const Teuchos::ParameterList ¶ms=Teuchos::ParameterList()) | |
| Constructor. More... | |
| virtual | ~MonomialProjGramSchmidtPCEBasis2 () |
| Destructor. | |
Implementation of Stokhos::OrthogPolyBasis methods | |
| ordinal_type | order () const |
| Return order of basis. | |
| ordinal_type | dimension () const |
| Return dimension of basis. | |
| virtual ordinal_type | size () const |
| Return total size of basis. | |
| virtual const Teuchos::Array < value_type > & | norm_squared () const |
| Return array storing norm-squared of each basis polynomial. More... | |
| virtual const value_type & | norm_squared (ordinal_type i) const |
Return norm squared of basis polynomial i. | |
| virtual Teuchos::RCP < Stokhos::Sparse3Tensor < ordinal_type, value_type > > | computeTripleProductTensor () const |
| Compute triple product tensor. More... | |
|
virtual Teuchos::RCP < Stokhos::Sparse3Tensor < ordinal_type, value_type > > | computeLinearTripleProductTensor () const |
| Compute linear triple product tensor where k = 0,1,..,d. | |
| virtual value_type | evaluateZero (ordinal_type i) const |
Evaluate basis polynomial i at zero. | |
| virtual void | evaluateBases (const Teuchos::ArrayView< const value_type > &point, Teuchos::Array< value_type > &basis_vals) const |
Evaluate basis polynomials at given point point. More... | |
| virtual const std::string & | getName () const |
| Return string name of basis. | |
| virtual void | print (std::ostream &os) const |
Print basis to stream os. | |
Implementation of Stokhos::ReducedPCEBasis methods | |
| virtual void | transformToOriginalBasis (const value_type *in, value_type *out, ordinal_type ncol=1, bool transpose=false) const |
| Transform coefficients to original basis from this basis. | |
| virtual void | transformFromOriginalBasis (const value_type *in, value_type *out, ordinal_type ncol=1, bool transpose=false) const |
| Transform coefficients from original basis to this basis. | |
|
virtual Teuchos::RCP< const Stokhos::Quadrature < ordinal_type, value_type > > | getReducedQuadrature () const |
| Get reduced quadrature object. | |
 Public Member Functions inherited from Stokhos::ReducedPCEBasis< ordinal_type, value_type > Public Member Functions inherited from Stokhos::ReducedPCEBasis< ordinal_type, value_type > | |
| ReducedPCEBasis () | |
| Default constructor. | |
| virtual | ~ReducedPCEBasis () |
| Destructor. | |
 Public Member Functions inherited from Stokhos::OrthogPolyBasis< ordinal_type, value_type > Public Member Functions inherited from Stokhos::OrthogPolyBasis< ordinal_type, value_type > | |
| OrthogPolyBasis () | |
| Constructor. | |
| virtual | ~OrthogPolyBasis () |
| Destructor. | |
Protected Types | |
|
typedef Stokhos::CompletePolynomialBasisUtils < ordinal_type, value_type > | CPBUtils |
|
typedef Teuchos::SerialDenseVector < ordinal_type, value_type > | SDV |
|
typedef Teuchos::SerialDenseMatrix < ordinal_type, value_type > | SDM |
Protected Member Functions | |
| ordinal_type | buildQ (ordinal_type max_p, value_type threshold, const Teuchos::Array< Stokhos::OrthogPolyApprox< ordinal_type, value_type > > &pce, const Teuchos::RCP< const Stokhos::Quadrature< ordinal_type, value_type > > &quad, Teuchos::Array< Stokhos::MultiIndex< ordinal_type > > &terms_, Teuchos::Array< ordinal_type > &num_terms_, Teuchos::SerialDenseMatrix< ordinal_type, value_type > &Qp_, Teuchos::SerialDenseMatrix< ordinal_type, value_type > &A_, Teuchos::SerialDenseMatrix< ordinal_type, value_type > &F_) |
Build the reduced basis, parameterized by total order max_p. More... | |
Protected Attributes | |
| std::string | name |
| Name of basis. | |
| Teuchos::ParameterList | params |
| Algorithm parameters. | |
|
Teuchos::RCP< const Stokhos::OrthogPolyBasis < ordinal_type, value_type > > | pce_basis |
| Original pce basis. | |
| ordinal_type | pce_sz |
| Size of original pce basis. | |
| ordinal_type | p |
| Total order of basis. | |
| ordinal_type | d |
| Total dimension of basis. | |
| ordinal_type | sz |
| Total size of basis. | |
|
Teuchos::Array < Stokhos::MultiIndex < ordinal_type > > | terms |
| 2-D array of basis terms | |
| Teuchos::Array< ordinal_type > | num_terms |
| Number of terms up to each order. | |
| Teuchos::Array< value_type > | norms |
| Norms. | |
| SDM | Q |
| Values of transformed basis at quadrature points. | |
| SDM | Qp |
| Coefficients of transformed basis in original basis. | |
|
Teuchos::RCP< const Stokhos::Quadrature < ordinal_type, value_type > > | reduced_quad |
| Reduced quadrature object. | |
| bool | verbose |
| Whether to print a bunch of stuff out. | |
| value_type | rank_threshold |
| Rank threshold. | |
| std::string | orthogonalization_method |
| Orthogonalization method. | |
|
Teuchos::BLAS< ordinal_type, value_type > | blas |
Generate a basis from a given set of PCE expansions that is orthogonal with respect to the product measure induced by these expansions.
Given the PCE expansions, first build a non-orthogonal monomial basis. Orthogonalize this basis using Gram-Schmidt, then build a quadrature rule using the simplex method.
| Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::MonomialProjGramSchmidtPCEBasis2 | ( | ordinal_type | p, |
| const Teuchos::Array< Stokhos::OrthogPolyApprox< ordinal_type, value_type > > & | pce, | ||
| const Teuchos::RCP< const Stokhos::Quadrature< ordinal_type, value_type > > & | quad, | ||
| const Teuchos::ParameterList & | params = Teuchos::ParameterList() |
||
| ) |
Constructor.
| p | order of the basis |
| pce | polynomial chaos expansions defining new measure |
| quad | quadrature data for basis defining pce |
| Cijk | sparse triple product tensor for basis defining pce |
| sparse_tol | tolerance for dropping terms in sparse tensors |
References Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::buildQ(), Stokhos::ReducedQuadratureFactory< ordinal_type, value_type >::createReducedQuadrature(), Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::d, Stokhos::OrthogPolyBasis< ordinal_type, value_type >::dimension(), Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::norms, Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::num_terms, Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::params, Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::pce_basis, Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::Q, Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::Qp, Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::rank_threshold, Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::reduced_quad, Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::sz, and Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::terms.
|
protected |
Build the reduced basis, parameterized by total order max_p.
Returns resulting size of reduced basis
Referenced by Stokhos::MonomialProjGramSchmidtPCEBasis2< ordinal_type, value_type >::MonomialProjGramSchmidtPCEBasis2().
|
virtual |
Compute triple product tensor.
The 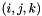 entry of the tensor
entry of the tensor 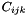 is given by
is given by 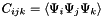 where
where 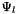 represents basis polynomial
represents basis polynomial 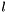 and
and 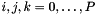 where
where 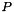 is size()-1.
is size()-1.
Implements Stokhos::OrthogPolyBasis< ordinal_type, value_type >.
|
virtual |
Evaluate basis polynomials at given point point.
Size of returned array is given by size(), and coefficients are ordered from order 0 up to size size()-1.
Implements Stokhos::OrthogPolyBasis< ordinal_type, value_type >.
|
virtual |
Return array storing norm-squared of each basis polynomial.
Entry 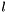 of returned array is given by
of returned array is given by 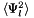 for
for 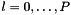 where
where 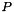 is size()-1.
is size()-1.
Implements Stokhos::OrthogPolyBasis< ordinal_type, value_type >.
 1.8.5
1.8.5